方べきの定理
方べきの定理
問題≪レギオモンタヌスの問題≫
水平面上の点 $\mathrm O$ の真上に相異なる $2$ 点 $\mathrm A,$ $\mathrm B$ をとる.
$\angle\mathrm{APB}$ が最大となるような水平面上の点 $\mathrm P$ に対して, $a = \mathrm{OA},$ $b = \mathrm{OB}$ を用いて距離 $\mathrm{OP}$ を表せ.
解答例
$2$ 点 $\mathrm A,$ $\mathrm B$ を通り, 直線 $\mathrm{OP}$ に点 $\mathrm T$ で接する円 $C$ を考える.
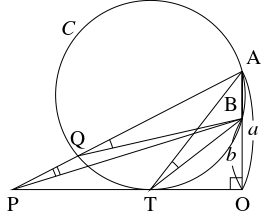$\mathrm P \neq \mathrm T$ のときは線分 $\mathrm{BP}$ と $C$ の交点を $\mathrm Q$ とおくと
\[\angle\mathrm{APB} < \angle\mathrm{AQB} = \angle\mathrm{ATB}\]
となってしまうから, $\mathrm P = \mathrm T$ である.
よって, 方べきの定理により
\[\mathrm{OP}^2 = \mathrm{OA}\cdot\mathrm{OB} = ab\]
であるから, $\mathrm{OP} = \sqrt{ab}$ である.
背景
本問は, 中世ドイツの天文学者・数学者のレギオモンタヌス(Regiomontanus)によって考え出された(1471 年).
本問に結果から, 高い建物の窓や, 高い位置に掲げられた絵画を見上げるとき, どの位置に立つのが最も好ましいのかが分かる.
三角関数の加法定理を使った別解については, こちらを参照されたい.