三角関数の加法定理
三角関数の加法定理
定理《三角関数の加法定理》
すべての角 $\alpha,$ $\beta$ に対して
\[\begin{aligned}
\cos (\alpha\pm\beta ) &= \cos\alpha\cos\beta\mp\sin\alpha\sin\beta, \\
\sin (\alpha\pm\beta ) &= \sin\alpha\cos\beta\pm\cos\alpha\sin\beta
\end{aligned}\]
が成り立つ.
また, $\alpha,$ $\beta,$ $\alpha\pm\beta$ が $\dfrac{\pi}{2}$ の倍数でないとき,
\[\tan (\alpha\pm\beta ) = \frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\]
が成り立つ.
証明
こちらを参照.
問題《余弦・正弦の加法定理》
- (A)
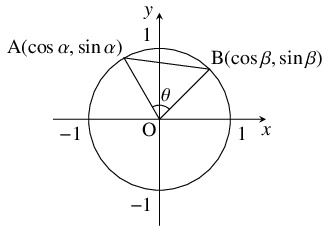
- 座標平面において原点を $\mathrm O$ とおき, 単位円周上の動点 $\mathrm A,$ $\mathrm B$ に対して, 動径 $\mathrm{OA},$ $\mathrm{OB}$ の表す角が $\alpha,$ $\beta$ であるとする. このとき, $\triangle\mathrm{OAB}$ に余弦定理を適用することで \[\cos (\alpha -\beta ) = \cos\alpha\cos\beta +\sin\alpha\sin\beta\] が成り立つことを示せ.
- (B)
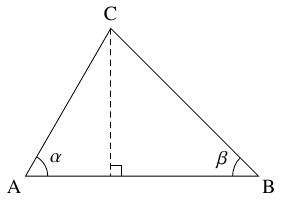
- 外接円の直径が $1$ の $\triangle\mathrm{ABC}$ において, $\alpha = \angle\mathrm A,$ $\beta = \angle\mathrm B$ とおく. このとき, 正弦定理と「第 $1$ 余弦定理」 \[\mathrm{AB} = \mathrm{BC}\cos\beta +\mathrm{CA}\cos\alpha \quad \cdots [\text B]\] を使って \[\sin (\alpha +\beta ) = \sin\alpha\cos\beta +\cos\alpha\sin\beta\] が成り立つことを示せ.
- (C)
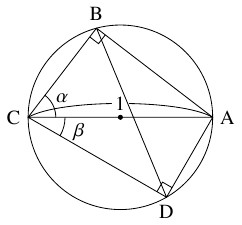
- $\alpha,$ $\beta$ が鋭角の場合に, 円に内接する四角形 $\mathrm{ABCD}$ を, $\mathrm{AC}$ が円の直径になり, $\angle\mathrm{ACB} = \alpha,$ $\angle\mathrm{ACD} = \beta,$ $\mathrm{AC} = 1$ となるようにとる. 正弦定理と「トレミーの定理」 \[\mathrm{AC}\cdot\mathrm{BD} = \mathrm{AB}\cdot\mathrm{CD}+\mathrm{BC}\cdot\mathrm{DA} \quad \cdots [\text C]\] を使って \[\sin (\alpha +\beta ) = \sin\alpha\cos\beta +\cos\alpha\sin\beta\] が成り立つことを示せ.
解答例
- (A)
- $\mathrm{OA},$ $\mathrm{OB}$ のなす角を $\theta$ $(0 \leqq \theta \leqq \pi )$ とおく.
このとき, ある整数 $n$ に対して $\alpha -\beta = \theta +2n\pi$ であり, $\mathrm A(\cos\alpha,\sin\alpha ),$ $\mathrm B(\cos\beta,\sin\beta )$ であるから, 余弦定理により \[\begin{aligned} &\cos (\alpha -\beta ) = \cos\theta = \frac{\mathrm{OA}^2+\mathrm{OB}^2-\mathrm{AB}^2}{2\mathrm{OA}\cdot\mathrm{OB}} \\ &= \frac{1^2+1^2-\{ (\cos\beta -\cos\alpha )^2+(\sin\beta -\sin\alpha )^2\}}{2\cdot 1\cdot 1} \\ &= \frac{2-(1+1-2\cos\alpha\cos\beta -2\sin\alpha\sin\beta )}{2} \\ &= \cos\alpha\cos\beta +\sin\alpha\sin\beta \end{aligned}\] が成り立つ.
- (B)
- \[\sin\angle\mathrm C = \sin (\pi -\alpha -\beta ) = \sin (\alpha +\beta )\]
であるから, 正弦定理により
\[\mathrm{BC} = \sin\alpha, \quad \mathrm{CA} = \sin\beta, \quad \mathrm{AB} = \sin (\alpha\!+\!\beta )\]
が成り立つ.
これらを $[\text B]$ に代入すると,
\[\sin (\alpha +\beta ) = \sin\alpha\cos\beta +\cos\alpha\sin\beta\]
が得られる.
- (C)
- 正弦定理により
\[\mathrm{BD} = \sin (\alpha +\beta )\]
であり, $\triangle\mathrm{ABC},$ $\triangle\mathrm{ADC}$ は直角三角形であるから
\[\mathrm{AB} = \sin\alpha,\ \mathrm{BC} = \cos\alpha,\ \mathrm{CD} = \cos\beta,\ \mathrm{DA} = \sin\beta\]
が成り立つ.
これらを $[\text C]$ に代入すると, \[\sin (\alpha +\beta ) = \sin\alpha\cos\beta +\cos\alpha\sin\beta\] が得られる.
参考
- 「第一余弦定理」と区別するとき, 余弦定理を「第二余弦定理」と呼ぶ.
- 古代ローマの天文学者トレミー (プトレマイオス) は「トレミーの定理」を使って「弦」$\mathrm{crd}\,\theta = 2\sin\dfrac{\theta}{2}$ に関する数表を作成した.
問題《正弦定理 $\Longrightarrow$ 第一余弦定理》
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C$ とおく.
「加比の理」
\[\frac{p}{q} = \frac{r}{s} = k \Longrightarrow \frac{px+ry}{qx+sy} = k\]
(証明はこちら) と正弦の加法定理を使って, 正弦定理から「第一余弦定理」
\[\begin{aligned}
a &= b\cos C+c\cos B, \\
b &= c\cos A+a\cos C, \\
c &= a\cos B+b\cos A
\end{aligned}\]
を導け.
解答例
正弦定理
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C},\]
により,
\[\begin{aligned}
\frac{a}{\sin A} &= \frac{b\cos C+c\cos B}{\sin B\cos C+\cos B\sin C} \quad (\because\text{「加比の理」}) \\
&= \frac{b\cos C+c\cos B}{\sin (B+C)} \quad (\because\text{正弦の加法定理})\\
&= \frac{b\cos C+c\cos B}{\sin A} \quad (\because A+B+C = \pi )
\end{aligned}\]
が得られる.
よって, $a = b\cos C+c\cos B$ が成り立つ.
同様に, $b = c\cos A+a\cos C,$ $c = a\cos B+b\cos A$ が成り立つ.
問題《正弦定理 $\Longrightarrow$ 第二余弦定理》
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C$ とおく.
余弦の加法定理を用いて, 正弦定理から「第二余弦定理」
\[\begin{aligned}
a^2 &= b^2+c^2-2bc\cos A, \\
b^2 &= c^2+a^2-2ca\cos B, \\
c^2 &= a^2+b^2-2ab\cos C
\end{aligned}\]
を導け.
解答例
正弦定理により
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = k\]
とおくと, $a = k\sin A,$ $b = k\sin B,$ $c = k\sin C$ となるから,
\[\begin{aligned}
&a^2-b^2-c^2 \\
&= k^2\sin ^2A-k^2\sin ^2B-k^2\sin ^2C \\
&= k^2\{\sin ^2(B+C)-\sin ^2B-\sin ^2C\} \\
&= k^2\{ (\sin B\cos C+\cos B\sin C)^2-\sin ^2B-\sin ^2C\} \\
&= k^2\{ (\sin ^2B\cos^2 C+\cos ^2B\sin ^2C \\
&\qquad +2\sin B\cos B\sin C\cos C)-\sin ^2B-\sin ^2C\} \\
&= k^2\{ 2\sin B\sin C\cos B\cos C \\
&\qquad -\sin ^2B(1-\cos ^2C)-(1-\cos ^2B)\sin ^2C\} \\
&= k^2(2\sin B\sin C\cos B\cos C-2\sin ^2B\sin ^2C) \\
&= 2(k\sin B)(k\sin C)(\cos B\cos C-\sin B\sin C) \\
&= 2bc\cos (B+C) \\
&= -2bc\cos A
\end{aligned}\]
となり, $a^2 = b^2+c^2-2bc\cos A$ が得られる. 残りの式も, 同様に証明できる.
参考
三角関数の加法定理のもとで, 正弦定理, 余弦定理 (「第一余弦定理」,「第二余弦定理」) は同値である (こちらとこちらを参照).
ここで, 加法定理は三角関数を特徴付ける内在的性質の $1$ つであるから, 正弦定理と余弦定理は本質的に同値な定理であると言える.
なお, ここでは, 正弦定理を「内角の正弦に対する対辺の長さの比が外接円の直径に等しい」という定理ではなく, 単に「内角の正弦に対する対辺の長さの比が互いに等しい」という定理として同値性を証明している.
問題《角の二等分線の傾き》
$a,$ $b$ を $b \neq \pm a$ なる実数とする.
$2$ 直線 $y = ax,$ $y = bx$ のなす角の二等分線の傾き $c$ を $a,$ $b$ で表す公式を, 正接の加法定理から導け.
解答例
$y = ax,$ $y = bx,$ 角の二等分線 $y = cx$ と $x$ 軸の正方向のなす角をそれぞれ $\alpha,$ $\beta$ $\gamma$ とおく.
このとき, $\beta -\gamma,$ $\gamma -\alpha$ は $\pi$ の倍数の差を除いて等しい.
つまり, ある整数 $n$ について,
\[ 2\gamma = \alpha +\beta +n\pi\]
となる.
よって, $\tan 2\gamma = \tan (\alpha +\beta )$ であるから, $2$ 倍角の公式, 加法定理により
\[\frac{2c}{1-c^2} = \frac{a+b}{1-ab}\]
が成り立つ.
分母を払い, $c$ について整理すると
\[ (a+b)c^2-2(ab-1)c-(a+b) = 0 \quad \cdots [\ast ]'\]
となるから, $2$ 次方程式の解の公式により
\[\begin{aligned}
c &= \frac{ab-1\pm\sqrt{(ab-1)^2+(a+b)^2}}{a+b} \\
&= \frac{ab-1\pm\sqrt{(a^2+1)(b^2+1)}}{a+b}
\end{aligned}\]
が得られる.
参考
問題《ナポレオンの定理》
$\triangle\mathrm{ABC}$ の外側に正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかき,
それらの重心をそれぞれ $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ とおく.
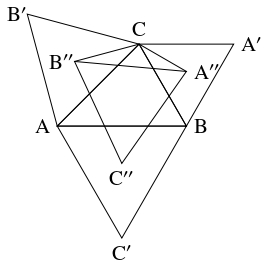
- (1)
- $\triangle\mathrm{ABC}$ の辺の長さ $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB}$ と外接円の半径 $R$ を用いて, $\mathrm A''\mathrm B''^2$ を表せ.
- (2)
- $\triangle\mathrm A''\mathrm B''\mathrm C''$ はどのような形の三角形か.

解答例
- (1)
- $\mathrm{CA}'',$ $\mathrm B''\mathrm C$ はそれぞれ正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA}$ の外接円の半径であるから, 正弦定理により \[\mathrm{CA}'' = \frac{a}{2\sin 60^\circ} = \frac{a}{\sqrt 3}, \quad \mathrm B''\mathrm C = \frac{b}{2\sin 60^\circ} = \frac{b}{\sqrt 3}\] である. また, $C = \angle\mathrm{ACB}$ とおくと \[\angle\mathrm A''\mathrm{CB}'' = C+60^\circ\] となるから, $\triangle\mathrm A''\mathrm B''\mathrm C$ に余弦定理を適用すると, 加法定理, 正弦定理 ($\triangle\mathrm{ABC}$ に適用) により \[\begin{aligned} &\mathrm A''\mathrm B''^2 \\ &= \left(\frac{a}{\sqrt 3}\right) ^2+\left(\frac{b}{\sqrt 3}\right) ^2-2\cdot\frac{a}{\sqrt 3}\cdot\frac{b}{\sqrt 3}\cos (C+60^\circ ) \\ &= \frac{a^2}{3}+\frac{b^2}{3}-\frac{2ab}{3}(\cos C\cos 60^\circ -\sin C\sin 60^\circ ) \\ &= \frac{a^2}{3}+\frac{b^2}{3}-\frac{2ab}{3}\left(\frac{a^2+b^2-c^2}{2ab}\cdot\frac{1}{2}-\frac{c}{2R}\cdot\frac{\sqrt 3}{2}\right) \\ &= \frac{R(a^2+b^2+c^2)+\sqrt 3abc}{6R} \quad \cdots [1] \end{aligned}\] が得られる.
- (2)
- $[1]$ は $a,$ $b,$ $c$ に関する対称式であるから, $\mathrm A,$ $\mathrm B,$ $\mathrm C$ の置き換えを考えると \[\mathrm A''\mathrm B''^2 \!=\! \mathrm B''\mathrm C''^2 \!=\! \mathrm C''\mathrm A''^2 \!=\! \frac{R(a^2\!+\!b^2\!+\!c^2)\!+\!\sqrt 3abc}{6R}\] が得られる. よって, $\triangle\mathrm A''\mathrm B''\mathrm C''$ は正三角形である.
参考
- 本問において $\triangle\mathrm A''\mathrm B''\mathrm C''$ が正三角形になることは, ナポレオンによって発見されたといわれ,「ナポレオンの定理」(Napoleon's theorem) として知られている.
- 複素数平面を利用した証明については, こちらを参照されたい.
- $\triangle\mathrm{ABC}$ の内側に正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかいても, それらの重心を結ぶ三角形 $\mathrm A''\mathrm B''\mathrm C''$ は正三角形になることが, 上記と同様に証明できる ($C+60^\circ,$ $\sqrt 3abc$ がそれぞれ $C-60^\circ,$ $-\sqrt 3abc$ になる). このことも「ナポレオンの定理」として知られている.
- また, 前者の正三角形と後者の正三角形の面積の差は, \[\begin{aligned} &\frac{1}{2}\cdot\frac{R(a^2+b^2+c^2)+\sqrt 3abc}{6R}\,\sin 60^\circ \\ &-\frac{1}{2}\cdot\frac{R(a^2+b^2+c^2)-\sqrt 3abc}{6R}\,\sin 60^\circ \\ &= 2\cdot\frac{1}{2}\cdot\frac{\sqrt 3abc}{6R}\cdot\frac{\sqrt 3}{2} \\ &= \frac{abc}{4R} \end{aligned}\] で, $\triangle\mathrm{ABC}$ の面積に等しい.
問題《ヘロンの公式とブラーマグプタの公式》
次のことを示せ.
- (1)
- $0$ より大きく $\pi$ より小さい, $\dfrac{\pi}{2}$ でない実数 $\alpha,$ $\beta,$ $\gamma$ が $\alpha +\beta +\gamma = \pi$ を満たすとき, \[\tan\alpha\tan\beta\tan\gamma = \tan\alpha +\tan\beta +\tan\gamma\] が成り立つ.
- (2)
- $\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $s = \dfrac{a+b+c}{2},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C,$ $S = \triangle\mathrm{ABC}$ とおく.
また, 内接円の中心を $\mathrm I,$ 半径を $r$ とおき, 内接円と辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の接点をそれぞれ $\mathrm A',$ $\mathrm B',$ $\mathrm C'$ とおく.
このとき,
- ①
- $\mathrm{AB}' = s-a$
- ②
- $\displaystyle\tan\left(\frac{\pi}{2}-\frac{A}{2}\right) = \frac{s-a}{r}$
- ③
- $S = \sqrt{s(s-a)(s-b)(s-c)}$
- (3)
- 円に内接する四角形 $\mathrm{ABCD}$ において, $a = \mathrm{AB},$ $b = \mathrm{BC},$ $c = \mathrm{CD},$ $d = \mathrm{DA},$ $s = \dfrac{a+b+c+d}{2}$ とおき, 四角形 $\mathrm{ABCD}$ の面積を $S$ とおく.
また, 辺 $\mathrm{AB}$ の $\mathrm A$ を超える延長と辺 $\mathrm{CD}$ の $\mathrm D$ を超える延長が点 $\mathrm E$ で交わるとし, $p = \mathrm{EA},$ $q = \mathrm{ED}$ とおき, $\triangle\mathrm{EDA}$ の面積を $T$ とおく.
このとき,
- ①
- $S:T = (b^2-d^2):d^2$
- ②
- $(b-d)(p+q) = d(c+a),$ $(b+d)(p-q) = d(c-a)$
- ③
- $S = \sqrt{(s-a)(s-b)(s-c)(s-d)}$
解答例
- (1)
- $\alpha +\beta +\gamma = \pi$ であるから, 加法定理により \[\begin{aligned} \tan\gamma &= \tan (\pi -\alpha -\beta ) = -\tan (\alpha +\beta ) \\ &= -\frac{\tan\alpha +\tan\beta}{1-\tan\alpha\tan\beta} \end{aligned}\] が成り立つ. 分母を払って整理すると, \[\begin{aligned} (\tan\alpha\tan\beta -1)\tan\gamma &= \tan\alpha +\tan\beta \\ \tan\alpha\tan\beta\tan\gamma &= \tan\alpha +\tan\beta +\tan\gamma \end{aligned}\] が得られる.
- (2)
- ①
- $\mathrm{AB}' = \mathrm{AC}',$ $\mathrm{BC}' = \mathrm{BA}',$ $\mathrm{CA}' = \mathrm{CB}'$ から
\[\begin{aligned}
2s-a &= b+c = \mathrm{CB}'+\mathrm{AB}'+\mathrm{AC}'+\mathrm{BC}' \\
&= 2\mathrm{AB}'+\mathrm{BA}'+\mathrm{CA}' = 2\mathrm{AB}'+a
\end{aligned}\]
であるので, $\mathrm{AB}' = s-a$ が成り立つ.
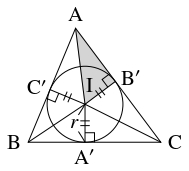
- ②
- $\triangle\mathrm{AIB}'$ に着目すると, \[\tan\left(\frac{\pi}{2}-\frac{A}{2}\right) = \tan\angle\mathrm{AIB}' = \frac{s-a}{r}\] が得られる.
- ③
- 同様に, \[\tan\left(\frac{\pi}{2}-\frac{B}{2}\right) = \frac{s-b}{r}, \quad \tan\left(\frac{\pi}{2}-\frac{C}{2}\right) = \frac{s-c}{r}\] が成り立つ. また, $\displaystyle\left(\frac{\pi}{2}-\frac{A}{2}\right) +\left(\frac{\pi}{2}-\frac{B}{2}\right) +\left(\frac{\pi}{2}-\frac{C}{2}\right) = \pi$ であるから, (1) により \[\begin{aligned} &\tan\left(\frac{\pi}{2}-\frac{A}{2}\right)\tan\left(\frac{\pi}{2}-\frac{B}{2}\right)\tan\left(\frac{\pi}{2}-\frac{C}{2}\right) \\ &= \tan\left(\frac{\pi}{2}-\frac{A}{2}\right) +\tan\left(\frac{\pi}{2}-\frac{B}{2}\right) +\tan\left(\frac{\pi}{2}-\frac{C}{2}\right) \end{aligned}\] が成り立つ. よって, \[\begin{aligned} \frac{s-a}{r}\cdot\frac{s-b}{r}\cdot\frac{s-c}{r} &= \frac{s-a}{r}+\frac{s-b}{r}+\frac{s-c}{r} \\ s(s-a)(s-b)(s-c) &= r^2s^2 \quad (\because 3s-a-b-c = s) \end{aligned}\] であるから, \[\begin{aligned} S &= \frac{ar}{2}+\frac{br}{2}+\frac{cr}{2} = r\cdot\frac{a+b+c}{2} = rs \\ &= \sqrt{s(s-a)(s-b)(s-c)} \end{aligned}\] が成り立つ.
- (3)
- ①
- $\angle\mathrm{EDA} = \angle\mathrm{EBC}$ であるから, $\triangle\mathrm{EDA},$ $\triangle\mathrm{EBC}$ は $d:b$ の比で相似である.
よって, \[ T:(T+S) = d^2:b^2\] から \[ S:T = (b^2-d^2):d^2\] である.
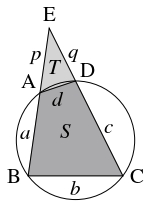
- ②
- \[ p:(q+c) = d:b, \quad q:(p+a) = d:b\] であるから, \[ bp = d(q+c), \quad bq = d(p+a)\] が成り立つ. 辺々の和, 差をとると, \[ (b-d)(p+q) = d(c+a), \quad (b+d)(p-q) = d(c-a)\] が得られる.
- ③
- $\triangle\mathrm{EDA}$ に (2) の公式を適用すると \[\begin{aligned} S^2 &= \frac{(b^2-d^2)^2}{d^4}T^2 \\ &= \frac{(b+d)^2(b-d)^2}{d^4}\cdot\frac{d+p+q}{2}\cdot\frac{p+q-d}{2} \\ &\qquad \cdot\frac{q+d-p}{2}\cdot\frac{d+p-q}{2} \\ &= \frac{(b-d)\{ (p+q)+d\}}{2d}\cdot\frac{(b+d)\{ (p+q)-d\}}{2d} \\ &\qquad \cdot\frac{(b+d)\{ d-(p-q)\}}{2d}\cdot\frac{(b-d)\{ d+(p-q)\}}{2d} \\ &= \frac{d(c+a)+d(b-d)}{2d}\cdot\frac{d(c+a)-d(b-d)}{2d} \\ &\qquad \cdot\frac{d(b+d)-d(c-a)}{2d}\cdot\frac{d(b+d)+d(c-a)}{2d} \\ &= \frac{c+a+b-d}{2}\cdot\frac{c+a-b+d}{2} \\ &\qquad \cdot\frac{b+d-c+a}{2}\cdot\frac{b+d+c-a}{2} \\ &= (s-a)(s-b)(s-c)(s-d) \end{aligned}\] となるから, \[ S = \sqrt{(s-a)(s-b)(s-c)(s-d)}\] が成り立つ.
参考
問題《オノの不等式》
直角三角形でない $\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C,$ $S = \triangle\mathrm{ABC}$ とおく.
次のことを示せ.
ただし, $x,$ $y,$ $z \geqq 0$ のとき $x+y+z \geqq 3\sqrt[3]{xyz}$ が成り立つこと (こちらとこちらを参照) は, 証明なしに使ってよい.
- (1)
- $\tan A\tan B\tan C = \tan A+\tan B+\tan C$ が成り立つ.
- (2)
- $\triangle\mathrm{ABC}$ が鋭角三角形のとき, \[ (4S)^6 \geqq 27(b^2+c^2-a^2)^2(c^2+a^2-b^2)^2(a^2+b^2-c^2)^2\] が成り立つ.
解答例
- (1)
- $A+B+C = \pi$ であるから, 加法定理により \[\begin{aligned} \tan C &= \tan (\pi -A-B) = -\tan (A+B) \\ &= -\frac{\tan A+\tan B}{1-\tan A\tan B} \end{aligned}\] が成り立つ. 分母を払って整理すると, \[\begin{aligned} (\tan A\tan B-1)\tan C &= \tan A+\tan B \\ \tan A\tan B\tan C &= \tan A+\tan B+\tan C \end{aligned}\] が得られる.
- (2)
- $\triangle\mathrm{ABC}$ が鋭角三角形であるとする. $A,$ $B,$ $C \neq \dfrac{\pi}{2}$ であることに注意すると, 余弦定理, 三角形の面積の公式により, \[\begin{aligned} &(4S)^6 \geqq 27(b^2+c^2-a^2)^2(c^2+a^2-b^2)^2(a^2+b^2-c^2)^2 \\ &\iff \frac{4S^2}{b^2c^2}\frac{4S^2}{c^2a^2}\frac{4S^2}{a^2b^2} \\ &\quad \geqq 27\frac{(b^2+c^2-a^2)^2}{4b^2c^2}\frac{(c^2+a^2-b^2)^2}{4c^2a^2}\frac{(a^2+b^2-c^2)^2}{4a^2b^2} \\ &\iff \sin ^2A\sin ^2B\sin ^2C \geqq 27\cos ^2A\cos ^2B\cos ^2C \\ &\iff \tan ^2A\tan ^2B\tan ^2C \geqq 27 \quad \cdots [1] \end{aligned}\] が得られる. ここで, $\tan A,$ $\tan B,$ $\tan C > 0$ であることに注意すると, 相加・相乗平均の不等式により, \[\tan A+\tan B+\tan C \geqq 3\sqrt[3]{\tan A\tan B\tan C} \quad \cdots [2]\] が得られる. (1) により \[\begin{aligned} [2] &\iff \tan A\tan B\tan C \geqq 3\sqrt[3]{\tan A\tan B\tan C} \\ &\iff \tan ^3A\tan ^3B\tan ^3C \geqq 27\tan A\tan B\tan C \\ &\iff [1] \end{aligned}\] が成り立つから, 求める不等式が得られる.
参考
(2) の不等式は「オノの不等式」(Ono's inequality) として知られている.
鈍角三角形においては成り立つとは限らない.
例えば, $a = 2,$ $b = 3,$ $c = 4$ なる $\triangle\mathrm{ABC}$ において,
\[\begin{aligned}
\cos C &= \frac{2^2+3^2-4^2}{2\cdot 2\cdot 3} = -\frac{1}{4}, \\
\sin C &= \sqrt{1-\cos ^2C} = \frac{\sqrt{15}}{4}
\end{aligned}\]
から
\[ S = \frac{1}{2}ab\sin C = \frac{1}{2}\cdot 2\cdot 3\cdot\frac{\sqrt{15}}{4} = \frac{3\sqrt{15}}{4}\]
であり,
\[\begin{aligned}
b^2+c^2-a^2 &= 3^2+4^2-2^2 = 21, \\
c^2+a^2-b^2 &= 4^2+2^2-3^2 = 11, \\
a^2+b^2-c^2 &= -3
\end{aligned}\]
であるので, 不等式の左辺
\[ (3\sqrt{15})^6 = 3^9\cdot 5^3 = 3^7\cdot 1125\]
は不等式の右辺
\[ 27\cdot 21^2\cdot 11^2\cdot (-3)^2 = 3^7\cdot 7^2\cdot 11^2 = 3^7\cdot 5929\]
より小さい.
問題《すべての角の正接が整数であるような三角形》
$\triangle\mathrm{ABC}$ において, $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C$ とおく.
$\tan A,$ $\tan B,$ $\tan C$ がすべて整数であるとき, それらの値を求めよ.
(参考: $1984$ 一橋大)
解答例
$\triangle\mathrm{ABC}$ において, $\tan A,$ $\tan B,$ $\tan C$ が整数であるとする.
また, $A \leqq B \leqq C$ であるとする.
このとき,
\[ 3A \leqq A+B+C = \pi\]
から, $0 < A \leqq \dfrac{\pi}{3}$ である.
よって,
\[ 0 < \tan A \leqq \sqrt 3\]
であり, $\tan A$ は整数だから,
\[\tan A = 1\]
である.
また, $A = \pi -(B+C)$ から,
\[ 1 = -\tan (B+C) = -\frac{\tan B+\tan C}{1-\tan B\tan C}\]
が成り立つ.
よって,
\[\begin{aligned}
\tan B\tan C-\tan B-\tan C-1 &= 0 \\
(\tan B-1)(\tan C-1) &= 2
\end{aligned}\]
となる.
$\tan B,$ $\tan C$ が整数であること,
$\dfrac{\pi}{4} = A \leqq B \leqq C$ から $B,$ $C$ は鋭角であって $\tan B \leqq \tan C$ であることに注意すると,
\[\tan B = 2, \quad \tan C = 3\]
である.
$A \leqq B \leqq C$ という条件を忘れると, 求める値は
\[\{\tan A,\ \tan B,\ \tan C\} = \{ 1,\ 2,\ 3\}\]
である.
問題《レギオモンタヌスの問題》
水平面上の点 $\mathrm O$ の真上に相異なる $2$ 点 $\mathrm A,$ $\mathrm B$ をとる ($\mathrm A$ は $\mathrm B$ より上方にあるとする).
$\mathrm A,$ $\mathrm B$ を見た仰角の差が最大になるような水平面上の点 $\mathrm P$ について, $a = \mathrm{OA},$ $b = \mathrm{OB}$ を用いて距離 $\mathrm{OP}$ を表せ.
解答例
$\theta = \angle\mathrm{APB},$ $x = \mathrm{OP},$ $\alpha = \angle\mathrm{OPA},$ $\beta = \angle\mathrm{OPB}$ とおく.
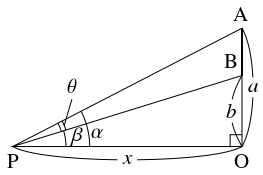 このとき, $0 < \theta < \dfrac{\pi}{2}$ であるから
このとき, $0 < \theta < \dfrac{\pi}{2}$ であるから

$\theta$ が最大 $\iff$ $\tan\theta$ が最大
が成り立ち,
\[\theta = \alpha -\beta, \quad \tan\alpha = \frac{a}{x}, \quad \tan\beta = \frac{b}{x}\]
であるから, 加法定理により
\[\begin{aligned}
\tan\theta &= \tan (\alpha -\beta ) = \frac{\tan\alpha -\tan\beta }{1+\tan\alpha\tan\beta} \\
&= \frac{\dfrac{a}{x}-\dfrac{b}{x}}{1+\dfrac{a}{x}\cdot\dfrac{b}{x}} = \frac{a-b}{x+\dfrac{ab}{x}}
\end{aligned}\]
が成り立つ.
よって, $\theta$ が最大になるのは, $x+\dfrac{ab}{x}$ が最小になるときである.
相加・相乗平均の不等式により $x+\dfrac{ab}{x}$ は $x = \dfrac{ab}{x},$ $x^2 = ab$ つまり $x = \sqrt{ab}$ の場合に限り最小値をとるから, 求める距離は $\mathrm{OP} = \sqrt{ab}$ である.
別解: 微分法 (数学 III) を利用
$\theta = \angle\mathrm{APB},$ $x = \mathrm{OP},$ $\alpha = \angle\mathrm{OPA},$ $\beta = \angle\mathrm{OPB}$ とおく.
このとき, $0 < \theta < \dfrac{\pi}{2}$ であるから
よって, $\tan\theta$ は $x = \sqrt{ab}$ の場合に限って, 極大かつ最大の値をとる.
ゆえに, 求める距離は $\mathrm{OP} = \sqrt{ab}$ である.
$\theta$ が最大 $\iff$ $\tan\theta$ が最大
が成り立ち,
\[\theta = \alpha -\beta, \quad \tan\alpha = \frac{a}{x}, \quad \tan\beta = \frac{b}{x}\]
であるから, 加法定理により
\[\begin{aligned}
\tan\theta &= \tan (\alpha -\beta ) = \frac{\tan\alpha -\tan\beta }{1+\tan\alpha\tan\beta} \\
&= \frac{\dfrac{a}{x}-\dfrac{b}{x}}{1+\dfrac{a}{x}\cdot\dfrac{b}{x}} = (a-b)\frac{x}{x^2+ab}
\end{aligned}\]
が成り立つ.
\[\frac{d}{dx}\tan\theta = (a-b)\frac{ab-x^2}{(x^2+ab)^2}\]
であるから,
\[\begin{aligned}
\frac{d}{dx}\tan\theta \geqq 0 &\iff 0 < x \leqq \sqrt{ab}, \\
\frac{d}{dx}\tan\theta \leqq 0 &\iff x \geqq \sqrt{ab}
\end{aligned}\]
が成り立つ.
| $x$ | $0$ | $\cdots$ | $\sqrt{ab}$ | $\cdots$ |
| $\dfrac{d}{dx}\tan\theta$ | $+$ | $0$ | $-$ | |
| $\tan\theta$ | $\nearrow$ | 極大 | $\searrow$ |
参考
- ここで解いた「レギオモンタヌスの問題」は, 中世ドイツの天文学者・数学者のレギオモンタヌス (Regiomontanus) によって考え出された ($1471$ 年). 本問に結果から, 高い建物の窓や高い位置に掲げられた絵画を見上げるとき, ラグビーのコンバージョン・キックでゴールを狙うとき (平面上で考察), どの位置に立つのが最も好ましいのかがわかる.
- 方べきの定理を使った別解については, こちらを参照されたい.
問題《余接の和の範囲》
$\theta$ が $\dfrac{\pi}{2}$ の倍数でないとき, $\cot\theta = \dfrac{1}{\tan\theta}$ と定める.
- (1)
- \[\cot (\pi -\theta ) = -\cot\theta,\ \cot (\alpha +\beta ) = \frac{\cot\alpha\cot\beta -1}{\cot\alpha +\cot\beta}\] が成り立つことを示せ.
- (2)
- $\triangle\mathrm{ABC}$ において \[\cot A+\cot B+\cot C \geqq \sqrt 3\] が成り立つことを示せ. また, 等号が成り立つのはどのようなときか答えよ.
解答例
- (1)
- \[\tan (\pi -\theta ) = -\tan\theta\] の両辺の逆数をとると, \[\cot (\pi -\theta ) = -\cot\theta\] が得られる. また, \[\tan (\alpha +\beta ) = \frac{\tan\alpha +\tan\beta}{1-\tan\alpha\tan\beta}\] の両辺の逆数をとると, \[\begin{aligned} &\cot (\alpha +\beta ) = \frac{1-\tan\alpha\tan\beta}{\tan\alpha +\tan\beta} \\ &= \frac{\dfrac{1}{\tan\alpha\tan\beta}-1}{\dfrac{1}{\tan\beta}+\dfrac{1}{\tan\alpha}} = \frac{\dfrac{1}{\tan\alpha}\cdot\dfrac{1}{\tan\beta}-1}{\dfrac{1}{\tan\alpha}+\dfrac{1}{\tan\beta}} \\ &= \frac{\cot\alpha\cot\beta -1}{\cot\alpha +\cot\beta} \end{aligned}\] が得られる.
- (2)
- 内角のうち $C$ が最大であるとして一般性を失わない. このとき, 頂点 $\mathrm C$ から直線 $\mathrm{AB}$ に下ろした垂線の足 $\mathrm H$ は辺 $\mathrm{AB}$ 上にある. $x = \mathrm{AH},$ $h = \mathrm{CH}$ とおくと, \[\cot A+\cot B = \frac{x}{h}+\frac{c-x}{h} = \frac{c}{h}\] から \[\begin{aligned} &\cot A+\cot B+\cot C \\ &= \cot A+\cot B+\cot (\pi -A-B) \\ &= \cot A+\cot B-\cot (A+B) \\ &= \cot A+\cot B-\frac{\cot A\cot B-1}{\cot A+\cot B} \\ &= \frac{c}{h}-\frac{\dfrac{x}{h}\cdot\dfrac{c-x}{h}-1}{\dfrac{c}{h}} = \frac{x^2-cx+c^2+h^2}{ch} \\ &= \frac{\left( x-\dfrac{c}{2}\right) ^2+\left(\dfrac{\sqrt 3}{2}c-h\right) ^2+\sqrt 3ch}{ch} \\ &= \frac{1}{ch}\left( x-\dfrac{c}{2}\right) ^2+\frac{1}{ch}\left(\dfrac{\sqrt 3}{2}c-h\right) ^2+\sqrt 3 \geqq \sqrt 3 \end{aligned}\] が成り立つ. 等号成立は $x = \dfrac{c}{2},$ $h = \dfrac{\sqrt 3}{2}c,$ つまり $\triangle\mathrm{ABC}$ が正三角形である場合に限る.
参考
- $\cot\theta$ を $\theta$ の「余接」(cotangent) と呼ぶ.
- $\triangle\mathrm{ABC}$ の内部にあり, $\angle\mathrm{PAB} = \angle\mathrm{PBC} = \angle\mathrm{PCA} = \theta,$ $\angle\mathrm P'\mathrm{AC} = \angle\mathrm P'\mathrm{CB} = \angle\mathrm P'\mathrm{BA} = \theta$ を満たす点 $\mathrm P,$ $\mathrm P'$ をそれぞれ「第 $1$ ブロカール点」(first Brocard point),「第 $2$ ブロカール点」(second Brocard point), $\theta$ を「ブロカール角」(Brocard angle) と呼ぶ. \[\cot\theta = \frac{a^2+b^2+c^2}{4S}\] であることが知られている (こちらを参照). 頂点 $\mathrm C$ から $\mathrm{AB}$ に下ろした垂線の長さを $h$ とおくと, $h = \dfrac{2S}{c}$ から \[\cot A+\cot B = \frac{c}{h} = \frac{c^2}{2S}\] となる. 同様に \[\cot B+\cot C = \frac{a^2}{2S}, \quad \cot C+\cot A = \frac{b^2}{2S}\] であるから, \[\cot\theta = \frac{a^2+b^2+c^2}{4S} = \cot A+\cot B+\cot C\] が成り立つ. 本問の結果により, $\theta \leqq 30^\circ$ であることがわかる.
- (2) の不等式は, \[ x^2y^2+y^2z^2+z^2x^2 \geqq xyz(x+y+z) \quad \cdots [\ast ]\] から得られる不等式 \[\begin{aligned} \left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2 &= \frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}+\frac{2}{xy}+\frac{2}{yz}+\frac{2}{zx} \\ &= \frac{x^2y^2+y^2z^2+z^2x^2}{x^2y^2z^2}+2\cdot\frac{x+y+z}{xyz} \\ &\geqq \frac{xyz(x+y+z)}{x^2y^2z^2}+2\cdot\frac{x+y+z}{xyz} \quad (\because [\ast ]) \\ &= 3\cdot\frac{x+y+z}{xyz} \\ \end{aligned}\] と等式 \[\tan A+\tan B+\tan C = \tan A\tan B\tan C\] を合わせることで示すこともできる (参考: $2024$ 浜松医科大). $[\ast ]$ は, \[\begin{aligned} &x^2y^2+y^2z^2+z^2x^2-xyz(x+y+z) \\ &= x^2y^2z^2\left(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}-\frac{1}{xy}-\frac{1}{yz}-\frac{1}{zx}\right) \\ &= \frac{x^2y^2z^2}{2}\left\{\left(\frac{1}{x}-\frac{1}{y}\right) ^2+\left(\frac{1}{y}-\frac{1}{z}\right) ^2+\left(\frac{1}{z}-\frac{1}{x}\right) ^2\right\} \geqq 0 \end{aligned}\] と示すことができる.
