三角関数の合成
三角関数の合成
定理《三角関数の合成》
実数 $a,$ $b$ に対して, $(a,b) \neq (0,0)$ ならば, $\alpha$ を
\[\cos\alpha = \frac{a}{\sqrt{a^2+b^2}}, \quad \sin\alpha = \frac{b}{\sqrt{a^2+b^2}}\]
を満たす角として
\[ a\sin\theta +b\cos\theta = \sqrt{a^2+b^2}\sin (\theta +\alpha )\]
が成り立つ.
証明
加法定理により,
\[\begin{aligned}
&a\sin\theta +b\cos\theta \\
&= \sqrt{a^2+b^2}\left(\sin\theta\cdot\frac{a}{\sqrt{a^2+b^2}}+\cos\theta\cdot\frac{b}{\sqrt{a^2+b^2}}\right) \\
&= \sqrt{a^2+b^2}(\sin\theta\cos\alpha +\cos\theta\sin\alpha ) \\
&= \sqrt{a^2+b^2}\sin (\theta +\alpha )
\end{aligned}\]
が成り立つ.
問題《円に内接する長方形の周長の最大値》
$xy$ 平面において, 単位円に内接し, 辺が座標軸に平行である長方形について,
第 $1$ 象限上の頂点の座標を $(\cos\theta,\sin\theta )$ $\left( 0 < \theta < \dfrac{\pi}{2}\right)$ とおき,
周の長さを $L$ とおく.
- (1)
- $\theta$ の関数として $L$ を表せ.
- (2)
- $L$ の最大値を求めよ.
解答例
- (1)
- 単位円に内接し, 辺が座標軸に平行である長方形の $4$ つの頂点は $(\pm\cos\theta,\pm\sin\theta )$ (複号任意) であるから, 周の長さ $L$ は
\[ L = 4\sin\theta +4\cos\theta\]
と表される.
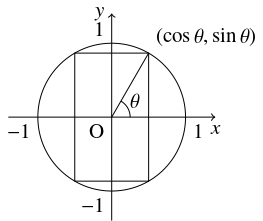
- (2)
- (1) の結果から \[\begin{aligned} L &= 4\sqrt 2\left(\sin\theta\cdot\frac{1}{\sqrt 2}+\cos\theta\cdot\frac{1}{\sqrt 2}\right) \\ &= 4\sqrt 2\sin\left(\theta +\frac{\pi}{4}\right) \end{aligned}\] であり, $0 < \theta < \dfrac{\pi}{2}$ から $\dfrac{\pi}{4} < \theta +\dfrac{\pi}{4} < \dfrac{3}{4}\pi$ であるので, $L$ は $\theta +\dfrac{\pi}{4} = \dfrac{\pi}{2}$ つまり $\theta = \dfrac{\pi}{4}$ のとき (正方形のとき), 最大値 $4\sqrt 2$ をとる.
参考
単位円に内接する $n$ 角形 $\mathrm P_1\cdots\mathrm P_n$ のうち, 周の長さ $L$ が最大になるものは正 $n$ 角形である.
実際, $\mathrm P_{n+1} = \mathrm P_1$ として, $\theta _k = \dfrac{1}{2}\angle\mathrm P_k\mathrm O\mathrm P_{k+1}$ とおくと,
\[\begin{aligned}
L &= \sum_{k = 1}^n\mathrm P_k\mathrm P_{k+1} = \sum_{k = 1}^n2\sin\theta _k = 2n\sum_{k = 1}^n\frac{\sin\theta _k}{n} \\
&\leqq 2n\sin\left(\sum_{k = 1}^n\frac{\theta _k}{n}\right) = 2n\sin\frac{\pi}{n}
\end{aligned}\]
となる.
ここで, 不等号は $\sin\theta$ $(0 < \theta < \pi )$ のグラフが上に凸 (微分法: 理系) であることから「イェンセンの不等式」により成り立ち, 等号成立は $\theta _1 = \cdots = \theta _n$ のとき (正 $n$ 角形のとき) に限る.
問題《単位正三角形に外接する正方形》
座標平面上に $1$ 辺の長さが $1$ の正三角形 $\mathrm{PQR}$ を $\mathrm P(\cos\theta,0),$ $\mathrm Q(0,\sin\theta )$ $\left( 0 \leqq \theta \leqq \dfrac{\pi}{4}\right)$ となるようにとり, $\mathrm R(f(\theta ),g(\theta ))$ とおく.
- (1)
- $\theta$ を用いて $f(\theta ),$ $g(\theta )$ を表せ.
- (2)
- 各 $\theta$ に対して $\cos\theta,$ $\sin\theta,$ $f(\theta ),$ $g(\theta )$ のうち最大の値を $M(\theta )$ とおく. $\theta$ を用いて $M(\theta )$ を表せ.
- (3)
- $M(\theta )$ の最小値を求めることにより, $1$ 辺の長さが $1$ の正三角形に外接する正方形の面積の最小値を求めよ. ただし, 正三角形と正方形は $1$ 点で頂点を共有するものとする.
解答例
- (1)
- $\mathrm{PR}$ と $x$ 軸のなす鋭角は $\dfrac{2}{3}\pi -\theta$ であるから, \[\begin{aligned} f(\theta ) &= \cos\theta +\cos\left(\frac{2}{3}\pi -\theta\right) = \cos\theta -\frac{1}{2}\cos\theta +\frac{\sqrt 3}{2}\sin\theta \\ &= \frac{\sqrt 3}{2}\sin\theta +\frac{1}{2}\cos\theta = \sin\left(\theta +\frac{\pi}{6}\right), \\ g(\theta ) &= \sin\left(\frac{2}{3}\pi -\theta\right) = \sin\left(\theta +\frac{\pi}{3}\right) \end{aligned}\] である.
- (2)
- $\cos\theta\,\left( = \sin\left(\theta +\dfrac{\pi}{2}\right)\right)$ と $\sin\theta,$ および $\sin\left(\theta +\dfrac{\pi}{6}\right)$ と $\sin\left(\theta +\dfrac{\pi}{3}\right)$ のグラフは, それぞれ互いに直線 $\theta = \dfrac{\pi}{4}$ に関して対称である. $0 \leqq \theta \leqq \dfrac{\pi}{4}$ において, $\cos\theta \geqq \sin\theta,$ $f(\theta ) \leqq g(\theta )$ であるから, $\cos\theta$ と $g(\theta )$ の大小を比較すると, \[ M(\theta ) = \begin{cases} \cos\theta & \left( 0 \leqq \theta \leqq \dfrac{\pi}{12}\right), \\[2mm] \sin\left(\theta +\dfrac{\pi}{3}\right) & \left(\dfrac{\pi}{12} < \theta \leqq \dfrac{\pi}{4}\right) \end{cases}\] であることがわかる.
- (3)
- $\cos\theta$ $\left( 0 \leqq \theta \leqq \dfrac{\pi}{12}\right)$ は $\theta = \dfrac{\pi}{12}$ のとき最小値をとり, $\sin\left(\theta +\dfrac{\pi}{3}\right)$ $\left(\dfrac{\pi}{12} < \theta \leqq \dfrac{\pi}{4}\right)$ は $\theta = \dfrac{\pi}{4}$ のとき最小値をとる. $\sin\dfrac{7}{12}\pi = \cos\dfrac{\pi}{12}$ であるから, これらの最小値は一致する. よって, $M(\theta )$ の最小値は, \[\begin{aligned} \cos\frac{\pi}{12} &= \cos\left(\frac{\pi}{4}-\frac{\pi}{6}\right) = \cos\frac{\pi}{4}\cos\frac{\pi}{6}+\sin\frac{\pi}{4}\sin\frac{\pi}{6} \\ &= \frac{\sqrt 2}{2}\cdot\frac{\sqrt 3}{2}+\frac{\sqrt 2}{2}\cdot\frac{1}{2} = \frac{\sqrt 6+\sqrt 2}{4} \end{aligned}\] である. $1$ 辺の長さが $1$ の正三角形 $\mathrm{PQR}$ は, 必要に応じて平行移動と回転移動, 直線 $y = x$ に関する対称移動を行うことにより, 上記のように配置できる. ゆえに, $1$ 辺の長さが $1$ の正三角形に外接する正方形 ($1$ 点で頂点を共有) の面積の最小値は, \[\left(\frac{\sqrt 6+\sqrt 2}{4}\right) ^2 = \frac{2+\sqrt 3}{4}\] である.
参考
- 本問の解について, 正方形と正三角形の面積の比は \[\left(\frac{\sqrt 6+\sqrt 2}{4}\right) ^2:\frac{1}{2}\cdot 1^2\cdot\frac{\sqrt 3}{2} = \frac{2+\sqrt 3}{4}:\frac{\sqrt 3}{4} = 1:(2\sqrt 3-3)\] であるから, $1$ 辺の長さが $1$ の正方形に含まれる正三角形の面積の最大値は $2\sqrt 3-3$ である.
- 正三角形に外接する最小の長方形 ($1$ 点で頂点を共有) を求めると, 上記の正方形が得られる (詳細は省略).
