三角関数の和・積の公式
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C$ とおく.
積和の公式
定理《三角関数の積和の公式》
\[\begin{aligned}
\cos\alpha\cos\beta &= \frac{\cos (\alpha +\beta )+\cos (\alpha -\beta )}{2}, \\
\sin\alpha\sin\beta &= \frac{\cos (\alpha -\beta )-\cos (\alpha +\beta )}{2}, \\
\sin\alpha\cos\beta &= \frac{\sin (\alpha +\beta )+\sin (\alpha -\beta )}{2}
\end{aligned}\]
が成り立つ.
証明
加法定理
\[\begin{aligned}
\cos (\alpha +\beta ) &= \cos\alpha\cos\beta -\sin\alpha\sin\beta \quad \cdots [1], \\
\cos (\alpha -\beta ) &= \cos\alpha\cos\beta +\sin\alpha\sin\beta \quad \cdots [2], \\
\sin (\alpha +\beta ) &= \sin\alpha\cos\beta +\cos\alpha\sin\beta \quad \cdots [3], \\
\sin (\alpha -\beta ) &= \sin\alpha\cos\beta -\cos\alpha\sin\beta \quad \cdots [4]
\end{aligned}\]
において, $[1]+[2],$ $[2]-[1],$ $[3]+[4]$ を $2$ で割ると, 求める等式が得られる.
問題《第一トレミーの定理》
すべての内角が $180^\circ$ 未満である四角形 $\mathrm{ABCD}$ が直径 $1$ の円に内接している.
弧 $\mathrm{AB},$ $\mathrm{BC},$ $\mathrm{CD},$ $\mathrm{DA}$ に対する円周角 (四角形 $\mathrm{ABCD}$ がある側の角) をそれぞれ $\alpha,$ $\beta,$ $\gamma,$ $\delta$ とおく.
- (1)
- $\alpha,$ $\beta,$ $\gamma$ を用いて $\mathrm{AC},$ $\mathrm{BD}$ を表せ.
- (2)
- $\mathrm{AC}\cdot\mathrm{BD} = \mathrm{AB}\cdot\mathrm{CD}+\mathrm{BC}\cdot\mathrm{DA}$ が成り立つことを示せ.
解答例
- (1)
- 正弦定理により, \[\begin{aligned} \mathrm{AC} &= \sin\angle\mathrm{CDA} \\ &= \sin (\angle\mathrm{ADB}+\angle\mathrm{BDC}) = \sin (\alpha +\beta ), \\ \mathrm{BD} &= \sin\angle\mathrm{DAB} \\ &= \sin (\angle\mathrm{BAC}+\angle\mathrm{CAD}) = \sin (\beta +\gamma ) \end{aligned}\] が成り立つ.
- (2)
- 正弦定理により \[\mathrm{AB} = \sin\alpha,\ \mathrm{BC} = \sin\beta,\ \mathrm{CD} = \sin\gamma,\ \mathrm{DA} = \sin\delta\] であるから, \[\sin (\alpha\!+\!\beta )\sin (\beta\!+\!\gamma ) \!=\! \sin\alpha\sin\gamma\!+\!\sin\beta\sin\delta\ \cdots [1]\] を示せばよい. 三角関数の積和公式と \[\begin{aligned} (\alpha +\beta )+(\beta +\gamma ) &= (\alpha +\beta +\gamma +\delta )+\beta -\delta \\ &= 2\pi +\beta -\delta \end{aligned}\] から \[\begin{aligned} &2\sin (\alpha +\beta )\sin (\beta +\gamma ) \\ &= \cos (\alpha +\beta -\beta -\gamma )-\cos (\alpha +\beta +\beta +\gamma ) \\ &= \cos (\alpha -\gamma )+\cos (\beta -\delta ) \end{aligned}\] が成り立ち, \[\alpha +\gamma = 2\pi -(\beta +\delta )\] から \[\begin{aligned} &2(\sin\alpha\sin\gamma +\sin\beta\sin\delta ) \\ &= \cos (\alpha\!-\!\gamma )-\cos (\alpha\!+\!\gamma )+\cos (\beta\!-\!\delta )+\cos (\beta\!+\!\delta ) \\ &= \cos (\alpha -\gamma )+\cos (\beta -\delta ) \end{aligned}\] が成り立つ. よって, $[1]$ が成り立つから, 求める等式が成り立つ.
参考
問題《紙が重なった部分の面積の最小値》
$1$ 辺の長さが $1$ である正方形の紙を $2$ 本の対角線の交点を通る直線で折るとき, 紙が重なった部分の面積の最小値を求めよ.
(参考: $2011$ 信州大)
解答例
$1$ 辺の長さが $1$ の正方形 $\mathrm{ABCD}$ の形をした紙を考える.
その対角線の交点を $\mathrm O,$ 辺 $\mathrm{AB}$ の中点を $\mathrm M$ とおく.
対称性により, $\mathrm O$ を通り $\mathrm{AM}$ と共有点をもつ直線 $l$ で折る場合について考えれば十分である.
$l$ と $\mathrm{AB}$ の交点を $\mathrm E$ とおき, $l$ に関して $\mathrm A,$ $\mathrm D$ と対称な点を $\mathrm A',$ $\mathrm D'$ とおく.
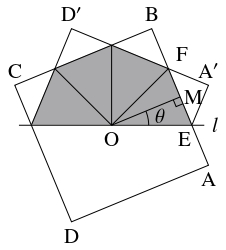 さらに, $\theta = \angle\mathrm{MOE}$ とおいて, 紙が重なった部分の面積を $S$ とおく.
このとき, $0 \leqq \theta \leqq \dfrac{\pi}{4}$ となる.
$0 < \theta \leqq \dfrac{\pi}{4}$ のとき, $\mathrm{AB},$ $\mathrm A'\mathrm D'$ の交点を $\mathrm F$ とおくと,
対称性と
\[\begin{aligned}
\mathrm{OE} &= \frac{\mathrm{OM}}{\cos\theta} = \frac{1}{2\cos\theta}\ \left(\because\mathrm{OM} = \dfrac{1}{2}\right), \\
\mathrm{OF} &= \frac{\mathrm{OM}}{\cos\left(\dfrac{\pi}{4}-\theta\right)} = \frac{1}{2\cos\left(\dfrac{\pi}{4}-\theta\right)}
\end{aligned}\]
であることから,
\[\begin{aligned}
S &= 4\triangle\mathrm{OEF} = 4\cdot\frac{1}{2}\mathrm{OE}\cdot\mathrm{OF}\sin\frac{\pi}{4}\ \left(\because\angle\mathrm{EOF} = \frac{\pi}{4}\right) \\
&= \frac{1}{2\sqrt 2\cos\theta\cos\left(\dfrac{\pi}{4}-\theta\right)} \quad \cdots [1]
\end{aligned}\]
が得られる.
これは $\theta = 0$ のときにも成り立つ.
$0 \leqq \theta \leqq \dfrac{\pi}{4}$ として, 積和の公式により $[1]$ を変形すると,
\[\begin{aligned}
S &= \frac{1}{\sqrt 2\left\{\cos\dfrac{\pi}{4}+\cos\left( 2\theta -\dfrac{\pi}{4}\right)\right\}} \\
&= \frac{1}{1+\sqrt 2\cos\left( 2\theta -\dfrac{\pi}{4}\right)}
\end{aligned}\]
が得られる.
ゆえに,
$S$ は, $2\theta -\dfrac{\pi}{4} = 0$ つまり $\theta = \dfrac{\pi}{8}$ のとき, 最小値 $\dfrac{1}{1+\sqrt 2} = \sqrt 2-1$ をとる.
さらに, $\theta = \angle\mathrm{MOE}$ とおいて, 紙が重なった部分の面積を $S$ とおく.
このとき, $0 \leqq \theta \leqq \dfrac{\pi}{4}$ となる.
$0 < \theta \leqq \dfrac{\pi}{4}$ のとき, $\mathrm{AB},$ $\mathrm A'\mathrm D'$ の交点を $\mathrm F$ とおくと,
対称性と
\[\begin{aligned}
\mathrm{OE} &= \frac{\mathrm{OM}}{\cos\theta} = \frac{1}{2\cos\theta}\ \left(\because\mathrm{OM} = \dfrac{1}{2}\right), \\
\mathrm{OF} &= \frac{\mathrm{OM}}{\cos\left(\dfrac{\pi}{4}-\theta\right)} = \frac{1}{2\cos\left(\dfrac{\pi}{4}-\theta\right)}
\end{aligned}\]
であることから,
\[\begin{aligned}
S &= 4\triangle\mathrm{OEF} = 4\cdot\frac{1}{2}\mathrm{OE}\cdot\mathrm{OF}\sin\frac{\pi}{4}\ \left(\because\angle\mathrm{EOF} = \frac{\pi}{4}\right) \\
&= \frac{1}{2\sqrt 2\cos\theta\cos\left(\dfrac{\pi}{4}-\theta\right)} \quad \cdots [1]
\end{aligned}\]
が得られる.
これは $\theta = 0$ のときにも成り立つ.
$0 \leqq \theta \leqq \dfrac{\pi}{4}$ として, 積和の公式により $[1]$ を変形すると,
\[\begin{aligned}
S &= \frac{1}{\sqrt 2\left\{\cos\dfrac{\pi}{4}+\cos\left( 2\theta -\dfrac{\pi}{4}\right)\right\}} \\
&= \frac{1}{1+\sqrt 2\cos\left( 2\theta -\dfrac{\pi}{4}\right)}
\end{aligned}\]
が得られる.
ゆえに,
$S$ は, $2\theta -\dfrac{\pi}{4} = 0$ つまり $\theta = \dfrac{\pi}{8}$ のとき, 最小値 $\dfrac{1}{1+\sqrt 2} = \sqrt 2-1$ をとる.

和積の公式
定理《三角関数の和積の公式》
\[\begin{aligned}
\cos A+\cos B &= 2\cos\frac{A+B}{2}\cos\frac{A-B}{2} \quad \cdots [1], \\
\cos A-\cos B &= -2\sin\frac{A+B}{2}\sin\frac{A-B}{2} \quad \cdots [2], \\
\sin A+\sin B &= 2\sin\frac{A+B}{2}\cos\frac{A-B}{2} \quad \cdots [3], \\
\sin A-\sin B &= 2\cos\frac{A+B}{2}\sin\frac{A-B}{2} \quad \cdots [4]
\end{aligned}\]
が成り立つ.
証明
積和の公式により
\[\begin{aligned}
\cos (\alpha +\beta )+\cos (\alpha -\beta ) &= 2\cos\alpha\cos\beta, \\
\cos (\alpha +\beta )-\cos (\alpha +\beta ) &= 2\sin\alpha\sin\beta, \\
\sin (\alpha +\beta )+\sin (\alpha -\beta ) &= 2\sin\alpha\cos\beta \quad \cdots [*]
\end{aligned}\]
であるから, $\alpha = \dfrac{A+B}{2},$ $\beta = \dfrac{A-B}{2}$ を代入すると, $[1]$~$[3]$ が得られる.
また, $[*]$ に $\alpha = \dfrac{A-B}{2},$ $\beta = \dfrac{A+B}{2}$ を代入すると,
\[\sin A+\sin (-B) = 2\sin\frac{A-B}{2}\cos\frac{A+B}{2}\]
となり, $[4]$ が得られる.
問題《正接定理》
$\triangle\mathrm{ABC}$ において
\[\frac{a-b}{a+b} = \frac{\sin A-\sin B}{\sin A+\sin B} = \frac{\tan\dfrac{A-B}{2}}{\tan\dfrac{A+B}{2}} = \tan\frac{A-B}{2}\tan\frac{C}{2}\]
が成り立つことを示せ.
解答例
$\triangle\mathrm{ABC}$ の外接円の半径を $R$ とおくと, 正弦定理により
\[ a = 2R\sin A, \quad b = 2R\sin B\]
となるから,
\[\frac{a-b}{a+b} = \frac{2R\sin A-2R\sin B}{2R\sin A+2R\sin B} = \frac{\sin A-\sin B}{\sin A+\sin B}\]
が得られる.
和積の公式により右辺を変形すると,
\[\begin{aligned}
&\frac{\sin A-\sin B}{\sin A+\sin B} \\
&= \frac{2\cos\dfrac{A+B}{2}\sin\dfrac{A-B}{2}}{2\sin\dfrac{A+B}{2}\cos\dfrac{A-B}{2}} = \frac{\sin\dfrac{A-B}{2}\div\cos\dfrac{A-B}{2}}{\sin\dfrac{A+B}{2}\div\cos\dfrac{A+B}{2}} \\
&= \frac{\tan\dfrac{A-B}{2}}{\tan\dfrac{A+B}{2}} = \frac{\tan\dfrac{A-B}{2}}{\tan\dfrac{\pi -C}{2}} = \frac{\tan\dfrac{A-B}{2}}{1\div\tan\dfrac{C}{2}} \\
&= \tan\frac{A-B}{2}\tan\frac{C}{2}
\end{aligned}\]
となる.
参考
等式 $\dfrac{a-b}{a+b} = \dfrac{\tan\dfrac{A-B}{2}}{\tan\dfrac{A+B}{2}}$ は「正接定理」として知られている.
問題《鋭角三角形の垂足三角形の周長と面積》
鋭角三角形 $\mathrm{ABC}$ において, $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C,$ $S = \triangle\mathrm{ABC}$ とおき, 外接円の半径を $R$ とおく.
また, 頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ から対辺に下ろした垂線の足をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおく.
- (1)
- $\mathrm{QR} = R\sin 2A$
- (2)
- $\mathrm{QR}+\mathrm{RP}+\mathrm{PQ} = 4R\sin A\sin B\sin C$
- (3)
- $\triangle\mathrm{AQR} = S\cos ^2A$
- (4)
- $\triangle\mathrm{PQR} = 2S\cos A\cos B\cos C$
解答例
- (1)
- $\mathrm{AH}$ は $\triangle\mathrm{AQR}$ の外接円の直径であるから, 正弦定理により \[\mathrm{QR} = \mathrm{AH}\sin A\] が成り立つ. また, \[\mathrm{AH} = 2\mathrm{OM} = 2R\cos A\] であるから, 倍角の公式により \[\mathrm{QR} = 2R\sin A\cos A = R\sin 2A\] が成り立つ.
- (2)
- (1) と同様の議論により, \[\mathrm{RP} = R\sin 2B, \quad \mathrm{PQ} = R\sin 2C\] が成り立つ. よって, 和積の公式により \[\begin{aligned} &\frac{\mathrm{QR}+\mathrm{RP}+\mathrm{PQ}}{R} \\ &= \sin 2A+\sin 2B+\sin 2C \\ &= 2\sin\frac{2A+2B}{2}\cos\frac{2A-2B}{2}+\sin 2(\pi -A-B) \\ &= 2\sin (A+B)\cos (A-B)-\sin 2(A+B) \\ &= 2\sin (A+B)\cos (A-B)-2\sin (A+B)\cos (A+B) \\ &= 2\{\cos (A-B)-\cos (A+B)\}\sin (A+B) \\ &= 2\cdot 2\sin A\sin B\sin (\pi -C) \\ &= 4\sin A\sin B\sin C \end{aligned}\] から, \[\mathrm{QR}+\mathrm{RP}+\mathrm{PQ} = 4R\sin A\sin B\sin C\] が得られる.
- (3)
- 直角三角形 $\mathrm{ABQ},$ $\mathrm{ACR}$ に着目すると, \[\begin{aligned} \triangle\mathrm{AQR} &= S\cdot\frac{\mathrm{AQ}}{\mathrm{AC}}\cdot\frac{\mathrm{AR}}{\mathrm{AB}} \\ &= S\cdot\frac{\mathrm{AB}\cos A}{\mathrm{AC}}\cdot\frac{\mathrm{AC}\cos A}{\mathrm{AB}} \\ &= S\cos ^2A \end{aligned}\] が得られる.
- (4)
- (2) と同様の議論により, \[\triangle\mathrm{BRP} = S\cos ^2B, \quad \triangle\mathrm{CPQ} = S\cos ^2C\] が成り立つ. $\triangle\mathrm{PQR} = S-\triangle\mathrm{AQR}-\triangle\mathrm{BRP}-\triangle\mathrm{CPQ}$ であるので, \[\begin{aligned} \frac{\triangle\mathrm{PQR}}{S} &= 1-\frac{\triangle\mathrm{AQR}}{S}-\frac{\triangle\mathrm{BRP}}{S}-\frac{\triangle\mathrm{CPQ}}{S} \\ &= 1-\cos ^2A-\cos ^2B-\cos ^2C \\ &= 1-\frac{1+\cos 2A}{2}-\frac{1+\cos 2B}{2}-\frac{1+\cos 2C}{2} \\ &= -\frac{\cos 2A+\cos 2B}{2}-\frac{1+\cos 2C}{2} \\ &= -\cos (A-B)\cos (A+B)-\cos ^2C \\ &= \cos (A-B)\cos C+\cos (A+B)\cos C \\ &\qquad\qquad\qquad\qquad (\because\cos (A+B) = -\cos C) \\ &= \{\cos (A-B)\cos (A+B)\}\cos C \\ &= 2\cos A\cos B\cos C \end{aligned}\] から, \[\triangle\mathrm{PQR} = 2S\cos A\cos B\cos C\] が得られる.
参考
- 三角形の各頂点から対辺に下ろした垂線の足を結ぶ三角形は「垂足三角形」(pedal triangle) と呼ばれる.
- 鋭角三角形の辺上の点を結ぶ三角形は「垂足三角形」のとき周の長さが最も短くなる.
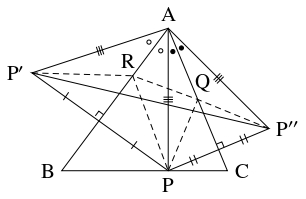
実際, 鋭角三角形 $\mathrm{ABC}$ の辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ 上の点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ について, $L = \mathrm{QR}+\mathrm{RP}+\mathrm{PQ}$ が最小になるのは $\mathrm{AP} \perp \mathrm{BC},$ $\mathrm{BQ} \perp \mathrm{CA},$ $\mathrm{CR} \perp \mathrm{AB}$ のときに限ることが, 次のように証明できる.
点 $\mathrm P$ を固定するとき, 辺 $\mathrm{AB},$ $\mathrm{AC}$ に関して点 $\mathrm P$ と対称な点 $\mathrm P',$ $\mathrm P''$ について
\[ L = \mathrm{QR}+\mathrm{RP}+\mathrm{PQ} = \mathrm{QR}+\mathrm{RP}'+\mathrm P''\mathrm Q \geqq \mathrm P'\mathrm P''\]
が成り立つから, $L$ が最小になるのは $\mathrm P'\mathrm P''$ が最小になるときに限り,
\[\mathrm P'\mathrm P'' = 2\mathrm{AP}\sin\angle\mathrm A \quad \left(\begin{array}{ll}\because & \mathrm{AP} = \mathrm{AP}' = \mathrm{AP}'', \\ {} & \angle\mathrm P'\mathrm A\mathrm P'' = 2\angle\mathrm A\end{array}\right)\]
であるから, それは $\mathrm{AP} \perp \mathrm{BC}$ のときに限る.
同様に, 点 $\mathrm Q$ を固定するとき $L$ が最小になるのは $\mathrm{BQ} \perp \mathrm{CA}$ ときに限り, 点 $\mathrm R$ を固定するとき $L$ が最小になるのは $\mathrm{CR} \perp \mathrm{AB}$ のときに限る.
- 鋭角三角形の垂心は「垂足三角形」の内心と一致し (こちらを参照), 鈍角三角形の垂心は「垂足三角形」の傍心と一致することが知られている.
- 本問で示した通り, $\triangle\mathrm{ABC}$ において, $\angle\mathrm A = A,$ $\angle\mathrm B = B,$ $\angle\mathrm C = C$ のとき, \[\begin{aligned} \cos A\cos B\cos C &= \frac{1}{2}(\sin ^2A+\sin ^2B+\sin ^2C-2) \\ &= \frac{1}{2}(1-\cos ^2A-\cos ^2B-\cos ^2C) \\ &= -\frac{1}{4}(1+\cos 2A+\cos 2B+\cos 2C), \\ \sin A\sin B\sin C &= \frac{1}{4}(\sin 2A+\sin 2B+\sin 2C) \end{aligned}\] が成り立つ.
問題《三角形の内角の余弦の和と正弦の和》
$A+B+C = \pi$ のとき
- (A)
- $\cos A+\cos B+\cos C = 1+4\sin\dfrac{A}{2}\sin\dfrac{B}{2}\sin\dfrac{C}{2}$
- (B)
- $\sin A+\sin B+\sin C = 4\cos\dfrac{A}{2}\cos\dfrac{B}{2}\cos\dfrac{C}{2}$
解答例
- (A)
- 和積の公式, 半角の公式により, \[\begin{aligned} &\cos A+\cos B+\cos C \\ &= 2\cos\frac{A-B}{2}\cos\frac{A+B}{2}+1-2\sin ^2\frac{C}{2} \\ &= 1+2\cos\frac{A-B}{2}\sin\frac{C}{2}-2\cos\frac{A+B}{2}\sin\frac{C}{2} \\ &\qquad\qquad\qquad\qquad\quad \left(\because\cos\frac{A+B}{2} = \sin\frac{C}{2}\right) \\ &= 1+2\left(\cos\frac{A-B}{2}-\cos\frac{A+B}{2}\right)\sin\frac{C}{2} \\ &= 1+4\sin\dfrac{A}{2}\sin\dfrac{B}{2}\sin\dfrac{C}{2} \end{aligned}\] が成り立つ.
- (B)
- 和積の公式, 倍角の公式により, \[\begin{aligned} &\sin A+\sin B+\sin C \\ &= 2\cos\frac{A-B}{2}\sin\frac{A+B}{2}+2\sin\frac{C}{2}\cos\frac{C}{2} \\ &= 2\cos\frac{A-B}{2}\cos\frac{C}{2}+2\cos\frac{A+B}{2}\cos\frac{C}{2} \\ &\qquad \left(\because\sin\frac{A+B}{2} = \cos\frac{C}{2},\ \cos\frac{A+B}{2} = \sin\frac{C}{2}\right) \\ &= 2\left(\cos\frac{A-B}{2}+\cos\frac{A+B}{2}\right)\cos\frac{C}{2} \\ &= 4\cos\dfrac{A}{2}\cos\dfrac{B}{2}\cos\dfrac{C}{2} \end{aligned}\] が成り立つ.
参考
三角形の幾何学において, 内角の余弦や正弦の和, 積は, 多くの公式に現れる.
問題《三角形の辺長の平方和と形状》
単位円周上の相異なる $3$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ に対して, 次のことを示せ.
- (1)
- $\mathrm{BC}^2+\mathrm{CA}^2+\mathrm{AB}^2 > 8$ ならば, $\triangle\mathrm{ABC}$ は鋭角三角形である.
- (2)
- $\mathrm{BC}^2+\mathrm{CA}^2+\mathrm{AB}^2 \leqq 9$ が成り立ち, 等号成立は $\triangle\mathrm{ABC}$ が正三角形であるときに限る.
(参考: $2002$ 京都大)
解答例
$a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C$ とおく.
仮定から $\triangle\mathrm{ABC}$ の外接円の半径は $1$ であるので, 正弦定理により
\[ a = 2\sin A, \quad b = 2\sin B, \quad c = 2\sin C \quad \cdots [1]\]
が成り立ち, これらの値は $2$ 以下である.
- (1)
- $a^2+b^2+c^2 > 8$ とする. \[\begin{aligned} b^2+c^2-a^2 &> (8-a^2)-a^2 = 2(2+a)(2-a) \geqq 0 \end{aligned}\] が成り立つから, $a^2 < b^2+c^2$ であり, $\angle\mathrm A$ は鋭角である. 同様に, $\angle\mathrm B,$ $\angle\mathrm C$ も鋭角であるから, $\triangle\mathrm{ABC}$ は鋭角三角形である.
- (2)
- $\triangle\mathrm{ABC}$ が鈍角三角形のとき, (1) の対偶により $a^2+b^2+c^2 \leqq 8$ が成り立つ. そこで, $\triangle\mathrm{ABC}$ を鋭角三角形とする. $[1]$ と倍角の公式, 和積の公式により, \[\begin{aligned} a^2+b^2+c^2 &= 4\sin ^2A+4\sin ^2B+4\sin ^2C \\ &= 4\sin ^2A+2(1-\cos 2B)+2(1-\cos 2C) \\ &= 4+4\sin ^2A-4\cos (B+C)\cos (B-C) \\ &= 4+4\sin ^2A+4\cos A\cos (B-C) \quad \cdots [2] \end{aligned}\] が成り立つ. $0 < B < \dfrac{\pi}{2},$ $0 < C < \dfrac{\pi}{2}$ から $-\dfrac{\pi}{2} < B-C < \dfrac{\pi}{2}$ であるので, $A$ を固定したとき $[2]$ の右辺は $B = C$ のとき最大値をとり, \[ a^2+b^2+c^2 \leqq 4+4\sin ^2A+4\cos A\] が成り立つ. 右辺を変形すると \[\begin{aligned} a^2+b^2+c^2 &\leqq 8-4\cos ^2A+4\cos A \\ &\leqq -4\left(\cos A-\frac{1}{2}\right) ^2+9 \\ &\leqq 9 \end{aligned}\] が得られ, 等号成立は $A = B = C = \dfrac{\pi}{3}$ つまり $\triangle\mathrm{ABC}$ が正三角形であるときに限る.
別解
原点を $\mathrm O$ とおき, $\vec a = \overrightarrow{\mathrm{OA}},$ $\vec b = \overrightarrow{\mathrm{OB}},$ $\vec c = \overrightarrow{\mathrm{OC}}$ とおく.
このとき,
\[\begin{aligned}
\mathrm{BC}^2+\mathrm{CA}^2+\mathrm{AB}^2 &= |\vec c-\vec b|^2+|\vec a-\vec c|^2+|\vec b-\vec a|^2 \\
&= 2(|\vec a|^2+|\vec b|^2+|\vec c|^2)-2(\vec b\cdot\vec c+\vec c\cdot\vec a+\vec a\cdot\vec b) \\
&= 6-2(\vec b\cdot\vec c+\vec c\cdot\vec a+\vec a\cdot\vec b) \quad \cdots [1]
\end{aligned}\]
である.
- (1)
- $\mathrm{BC}^2+\mathrm{CA}^2+\mathrm{AB}^2 > 8$ とする. $[1]$ により \[\begin{aligned} 6-2(\vec b\cdot\vec c+\vec c\cdot\vec a+\vec a\cdot\vec b) &> 8 \\ \vec b\cdot\vec c+\vec c\cdot\vec a+\vec a\cdot\vec b &< -1 \end{aligned}\] が成り立つ. よって, \[\begin{aligned} \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}} &= (\vec b-\vec a)\cdot (\vec c-\vec a) = \vec b\cdot\vec c-(\vec c\cdot\vec a+\vec a\cdot\vec b)+|\vec a|^2 \\ &> \vec b\cdot\vec c-(-1-\vec b\cdot\vec c)+1 = 2(1+\vec b\cdot\vec c) \\ &= 2(1+\cos\angle\mathrm{BOC}) \geqq 0 \end{aligned}\] から \[\cos\angle\mathrm A = \frac{\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}}{|\overrightarrow{\mathrm{AB}}||\overrightarrow{\mathrm{AC}}|} > 0\] であるので, $\angle\mathrm A$ は鋭角である. 同様に, $\angle\mathrm B,$ $\angle\mathrm C$ も鋭角であるから, $\triangle\mathrm{ABC}$ は鋭角三角形である.
- (2)
- $[1]$ により, \[\begin{aligned} &9-\mathrm{BC}^2+\mathrm{CA}^2+\mathrm{AB}^2 \\ &= 3+2(\vec b\cdot\vec c+\vec c\cdot\vec a+\vec a\cdot\vec b) \\ &= |\vec a|^2+|\vec b|^2+|\vec c|^2+2(\vec b\cdot\vec c+\vec c\cdot\vec a+\vec a\cdot\vec b) \\ &= |\vec a+\vec b+\vec c|^2 \geqq 0 \end{aligned}\] よって \[\mathrm{BC}^2+\mathrm{CA}^2+\mathrm{AB}^2 \leqq 9\] が成り立つ. 等号成立は $\vec a+\vec b+\vec c = \vec 0$ つまり $\dfrac{\vec a+\vec b+\vec c}{3} = \vec 0$ であるときに限り, それは $\triangle\mathrm{ABC}$ の重心と外心が一致する, つまり $\triangle\mathrm{ABC}$ が正三角形であるときに限る (証明はこちらを参照).
参考
$\triangle\mathrm{ABC}$ の内角が $\angle\mathrm A = A,$ $\angle\mathrm B = B,$ $\angle\mathrm C = C,$ 外接円の半径が $R$ であるとき, 本問で示したことから
\[\mathrm{BC}^2+\mathrm{CA}^2+\mathrm{AB}^2 \leqq 9R^2\]
つまり
\[\sin ^2A+\sin ^2B+\sin ^2C \leqq \frac{9}{4}\]
が成り立ち, 相互関係 $\cos ^2\theta +\sin ^2\theta = 1$ により
\[\cos ^2A+\cos ^2B+\cos ^2C \geqq \frac{3}{4}\]
も成り立つ.
問題《フォイエルバッハの定理》
正三角形でない $\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C$ とおき,
外心を $\mathrm O,$ 外接円の半径を $R,$ 内心を $\mathrm I,$ 内接円の半径を $r,$ 垂心を $\mathrm H,$ 線分 $\mathrm{OH}$ の中点を $\mathrm N$ とおく.
- (1)
- $R = (\triangle\mathrm{ABH}$ の外接円の半径$)$
- (2)
- $\mathrm{AH} = 2R\cos A$
- (3)
- $a = r\cos\dfrac{A}{2}\div\sin\dfrac{B}{2}\sin\dfrac{C}{2}$
- (4)
- $r = 4R\sin\dfrac{A}{2}\sin\dfrac{B}{2}\sin\dfrac{C}{2}$
- (5)
- $\mathrm{AI} = 4R\sin\dfrac{B}{2}\sin\dfrac{C}{2}$
- (6)
- $\mathrm{OH}^2 = R^2-8R^2\cos A\cos B\cos C$
- (7)
- $\mathrm{HI}^2 = 2r^2-4R^2\cos A\cos B\cos C$
- (8)
- $\mathrm{IN} = \dfrac{R}{2}-r$
(参考: 安藤哲哉『三角形と円の幾何学―数学オリンピック幾何問題完全攻略』)
解答例
- (1)
- 頂点 $\mathrm A,$ $\mathrm B$ から対辺またはその延長に下ろした垂線の足をそれぞれ $\mathrm A',$ $\mathrm B'$ とおく. $\triangle\mathrm{ABH}$ の外接円の半径を $R'$ とおくと, 正弦定理により \[ R = \frac{\mathrm{AB}}{2\sin C}, \quad R' = \frac{\mathrm{AB}}{2\sin\angle\mathrm{AHB}}\] となる. 四角形 $\mathrm A'\mathrm {HB}'\mathrm C$ は円に内接するから, $C = \pi -\angle\mathrm A'\mathrm{HB}' = \pi -\angle\mathrm{AHB}$ よって $\sin C = \sin\angle\mathrm{AHB}$ であり, $R = R'$ が成り立つ.
- (2)
- (1) に注意して $\triangle\mathrm{ABH}$ に正弦定理を適用すると, \[\begin{aligned} \mathrm{AH} &= 2R\sin\angle\mathrm{ABH} = 2R\sin\angle\mathrm{ABB}' \\ &= 2R\sin\left(\frac{\pi}{2}-A\right) = 2R\cos A \quad \cdots [1] \end{aligned}\] が得られる.
- (3)
- 内心 $\mathrm I$ から辺 $\mathrm{BC}$ に下ろした垂線の足を $\mathrm A''$ とおく. $a = \mathrm{BA}''+\mathrm A''\mathrm C,$ 正接の定義により \[\begin{aligned} a &= \frac{r}{\tan\dfrac{B}{2}}\!+\!\frac{r}{\tan\dfrac{C}{2}} = \dfrac{r\left(\tan\dfrac{B}{2}\!+\!\tan\dfrac{C}{2}\right)}{\tan\dfrac{B}{2}\tan\dfrac{C}{2}} \\ &= \frac{r\left(\sin\dfrac{B}{2}\cos\dfrac{C}{2}+\cos\dfrac{B}{2}\sin\dfrac{C}{2}\right)}{\sin\dfrac{B}{2}\sin\dfrac{C}{2}} \\ &= \frac{r\sin\left(\dfrac{B}{2}+\dfrac{C}{2}\right)}{\sin\dfrac{B}{2}\sin\dfrac{C}{2}} = \dfrac{r\sin\left(\dfrac{\pi}{2}-\dfrac{A}{2}\right)}{\sin\dfrac{B}{2}\sin\dfrac{C}{2}} \\ &= \frac{r\cos\dfrac{A}{2}}{\sin\dfrac{B}{2}\sin\dfrac{C}{2}} \quad \cdots [2] \end{aligned}\] となる.
- (4)
- $[2]$ と同様に, \[ b = \frac{r\cos\dfrac{B}{2}}{\sin\dfrac{C}{2}\sin\dfrac{A}{2}} \quad \cdots [2]', \quad c = \frac{r\cos\dfrac{C}{2}}{\sin\dfrac{A}{2}\sin\dfrac{B}{2}} \quad \cdots [2]''\] が成り立つ. また, 正弦定理, 倍角の公式により \[ a = 2R\sin A = 4R\sin\frac{A}{2}\cos\frac{A}{2} \quad \cdots [3]\] であり, 同様に \[ b \!=\! 4R\sin\frac{B}{2}\cos\frac{B}{2} \!\quad\! \cdots [3]', \quad c \!=\! 4R\sin\frac{C}{2}\cos\frac{C}{2} \!\quad\! \cdots [3]''\] が成り立つ. $[2],$ $[2]',$ $[2]'',$ $[3],$ $[3]',$ $[3]''$ の辺々を掛け合わせると \[\begin{aligned} abc &= \frac{r^3\cos\dfrac{A}{2}\cos\dfrac{B}{2}\cos\dfrac{C}{2}}{\sin ^2\dfrac{A}{2}\sin ^2\dfrac{B}{2}\sin ^2\dfrac{C}{2}} \\ &= 64R^3\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2} \end{aligned}\] から \[ r^3 = 64R^3\sin ^3\frac{A}{2}\sin ^3\frac{B}{2}\sin ^3\frac{C}{2}\] となるので, $R,$ $r,$ $\sin\dfrac{A}{2},$ $\sin\dfrac{B}{2},$ $\sin\dfrac{C}{2}$ が正であることに注意すると \[ r = 4R\sin\dfrac{A}{2}\sin\dfrac{B}{2}\sin\dfrac{C}{2} \quad \cdots [4]\] が得られる.
- (5)
- $\mathrm{AI} = r\div\sin\dfrac{A}{2}$ に $[4]$ を代入すると, \[\mathrm{AI} = \frac{4R\sin\dfrac{A}{2}\sin\dfrac{B}{2}\sin\dfrac{C}{2}}{\sin\dfrac{A}{2}} = 4R\sin\dfrac{B}{2}\sin\dfrac{C}{2} \quad \cdots [5]\] が得られる.
- (6)
- $\mathrm{AO}$ の延長と外接円の周の交点を $\mathrm B'''$ とおくと, $\angle\mathrm{ACB}''' = \dfrac{\pi}{2},$ 円周角の定理により $\angle\mathrm{AB}'''\mathrm C = B$ となるから, $\angle\mathrm{OAC} = \angle\mathrm B'''\mathrm{AC} = \dfrac{\pi}{2}-B$ となる. よって, \[\begin{aligned} &\angle\mathrm{OAH} = |\angle\mathrm{OAC}-\angle\mathrm{HAC}| \\ &= \left|\left(\frac{\pi}{2}-B\right) -\left(\frac{\pi}{2}-C\right)\right| = |C-B| \end{aligned}\] であるから, $\triangle\mathrm{AOH}$ に余弦定理を適用すると, $[1],$ 和積の公式により \[\begin{aligned} \mathrm{OH}^2 &= \mathrm{AO}^2+\mathrm{AH}^2-2\mathrm{AO}\cdot\mathrm{AH}\cos\angle\mathrm{OAH} \\ &= R^2+(2R\cos A)^2-2R\cdot 2R\cos A\cos |C-B| \\ &= R^2+4R^2\cos A\cos (\pi -B-C) \\ &\qquad -4R^2\cos A\cos (B-C) \\ &= R^2-4R^2\cos A\{ \cos (B+C)+\cos (B-C)\} \\ &= R^2-8R^2\cos A\cos B\cos C \quad \cdots [6] \end{aligned}\] が得られる.
- (7)
- \[\begin{aligned} \angle\mathrm{HAI} &= |\angle\mathrm{CAI}-\angle\mathrm{CAH}| = \left|\frac{A}{2}-\left(\frac{\pi}{2}-C\right)\right| \\ &= \left|\frac{A}{2}-\left(\frac{A+B+C}{2}-C\right)\right| = \left|\frac{C-B}{2}\right| \end{aligned}\] と, 余弦定理 ($\triangle\mathrm{AHI}$ に適用), $[1],$ $[5],$ 加法定理, 倍角の公式, 半角の公式, $[4]$ により \[\begin{aligned} &\mathrm{HI}^2 = \mathrm{AH}^2+\mathrm{AI}^2-2\mathrm{AH}\cdot\mathrm{AI}\cos\angle\mathrm{HAI} \\ &= (2R\cos A)^2+\left( 4R\sin\frac{B}{2}\sin\frac{C}{2}\right) ^2 \\ &\qquad -2\cdot 2R\cos A\cdot 4R\sin\frac{B}{2}\sin\frac{C}{2}\cdot\cos\left|\frac{C-B}{2}\right| \\ &= 4R^2\cos A\cos (\pi -B-C)+16R^2\sin ^2\frac{B}{2}\sin ^2\frac{C}{2} \\ &\qquad -16R^2\cos A\sin\frac{B}{2}\sin\frac{C}{2}\cos\left(\frac{B}{2}-\frac{C}{2}\right) \\ &= -4R^2\cos A\cos (B+C)+16R^2\sin ^2\frac{B}{2}\sin ^2\frac{C}{2} \\ &\qquad -16R^2\cos A\sin\frac{B}{2}\sin\frac{C}{2}\cos\frac{B}{2}\cos\frac{C}{2} \\ &\qquad -16R^2\cos A\sin ^2\frac{B}{2}\sin ^2\frac{C}{2} \\ &= -4R^2\cos A\cos (B+C)+16R^2\sin ^2\frac{B}{2}\sin ^2\frac{C}{2} \\ &\qquad -4R^2\cos A\sin B\sin C-16R^2\cos A\sin ^2\!\frac{B}{2}\sin ^2\!\frac{C}{2} \\ &= 16R^2(1-\cos A)\sin ^2\frac{B}{2}\sin ^2\frac{C}{2}-4R^2\cos A\cos B\cos C \\ &= 32R^2\sin ^2\frac{A}{2}\sin ^2\frac{B}{2}\sin ^2\frac{C}{2}-4R^2\cos A\cos B\cos C \\ &= 2r^2-4R^2\cos A\cos B\cos C \quad \cdots [7] \end{aligned}\] が得られる.
- (8)
- $\triangle\mathrm{IOH}$ とその中線 $\mathrm{IN}$ に「中線定理」を適用すると \[\mathrm{OI}^2+\mathrm{HI}^2 = 2\mathrm{IN}^2+\frac{1}{2}\mathrm{OH}^2\] となるから,「チャップル=オイラーの定理」, $[7],$ $[6]$ により \[\begin{aligned} &\mathrm{IN}^2 = \frac{1}{2}\mathrm{OI}^2+\frac{1}{2}\mathrm{HI}^2-\frac{1}{4}\mathrm{OH}^2 \\ &= \frac{1}{2}(R^2-2Rr)+\frac{1}{2}(2r^2-4R^2\cos A\cos B\cos C) \\ &\qquad -\frac{1}{4}(R^2-8R^2\cos A\cos B\cos C) \\ &= \frac{1}{4}R^2-Rr+r^2 = \left(\frac{R}{2}-r\right) ^2 \end{aligned}\] が得られる. $R \geqq 2r$ に注意すると, \[\mathrm{IN} = \frac{R}{2}-r\] であることがわかる.
参考
- (8) の結果は, 三角形の「九点円」(半径は外接円の半径の半分, こちらを参照) と内接円が接していることを示している. 「九点円」は $3$ つの傍接円に接していることもほぼ同様に証明できる. これらの事実は「フォイエルバッハの定理」(Feuerbach's theorem) として知られている.
- (4) の結果と \[\cos A+\cos B+\cos C = 1+4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}\] (こちらを参照) を合わせると, \[\cos A+\cos B+\cos C = 1+\frac{r}{R}\] が得られる. さらに, (2) の結果とこの等式を合わせると, \[\begin{aligned} \mathrm{AH}+\mathrm{BH}+\mathrm{CH} &= 2R(\cos A+\cos B+\cos C) \\ &= 2R\left( 1+\frac{r}{R}\right) = 2(R+r) \end{aligned}\] が得られる.
- (6), (7) の結果と \[\sin ^2A+\sin ^2B+\sin ^2C = 2+2\cos A\cos B\cos C\] (こちらを参照) を合わせると, 正弦定理により \[\begin{aligned} \mathrm{OH}^2 &= R^2-4R^2\cdot 2\cos A\cos B\cos C \\ &= R^2-4R^2(\sin ^2A+\sin ^2B+\sin ^2C-2) \\ &= 9R^2-\{ (2R\sin A)^2+(2R\sin B)^2+(2R\sin C)^2\} \\ &= 9R^2-(a^2+b^2+c^2), \\ \mathrm{IH}^2 &= 2r^2-2R^2\cdot 2\cos A\cos B\cos C \\ &= 2r^2-2R^2(\sin ^2A+\sin ^2B+\sin ^2C-2) \\ &= 4R^2+2r^2 \\ &\qquad -\frac{1}{2}\{ (2R\sin A)^2+(2R\sin B)^2+(2R\sin C)^2\} \\ &= 4R^2+2r^2-\frac{1}{2}(a^2+b^2+c^2) \end{aligned}\] が得られる. これから \[\begin{aligned} a^2+b^2+c^2 &\leqq 9R^2, \\ a^2+b^2+c^2 &\leqq 8R^2+4r^2 \end{aligned}\] であることもわかる.
