ベクトルの内積
ベクトルの内積
定理《ベクトルの内積の成分表示》
$n = 2$ または $n = 3$ とする.
ベクトル $\vec a = (a_1,\cdots,a_n),$ $\vec b = (b_1,\cdots,b_n)$ に対して,
\[\vec a\cdot\vec b = a_1b_1+\cdots +a_nb_n\]
が成り立つ.
証明
$\vec a,$ $\vec b \neq \vec 0,$ のとき, $\vec a,$ $\vec b$ のなす角を $\theta$ とおくと, 余弦定理により
\[\begin{aligned}
\vec a\cdot\vec b &= |\vec a||\vec b|\cos\theta \\
&= |\vec a||\vec b|\cdot\frac{|\vec a|^2+|\vec b|^2-|\vec b-\vec a|^2}{2|\vec a||\vec b|} \\
&= \frac{\displaystyle\sum_{k = 1}^na_k{}^2+\sum_{k = 1}^nb_k{}^2-\sum_{k = 1}^n(b_k-a_k)^2}{2} \\
&= \frac{\displaystyle\sum_{k = 1}^na_k{}^2+\sum_{k = 1}^nb_k{}^2-\sum_{k = 1}^n(b_k{}^2-2a_kb_k+a_k{}^2)}{2} \\
&= \sum_{k = 1}^na_kb_k
\end{aligned}\]
が成り立つ.
参考
一般の「有限次元空間」のベクトルに内積の概念を拡張するとき, この定理の等式をベクトルの内積の定義として採用する (この等式のほうが, 内積の性質を調べるのに適している).
こちらを定義として採用した場合, 内積の性質から
\[ |\vec b-\vec a|^2 = |\vec b|^2-2\vec a\cdot\vec b+|\vec a|^2\]
であることがわかる.
$\vec a \neq \vec 0,$ $\vec b \neq \vec 0$ で $\vec a,$ $\vec b$ のなす角が $\theta$ であるとき, 余弦定理により
\[ |\vec b-\vec a|^2 = |\vec a|^2+|\vec b|^2-2|\vec a||\vec b|\cos\theta\]
が成り立つから,
\[\vec a\cdot\vec b = |\vec a||\vec b|\cos\theta\]
が得られる.
問題《ベクトルによるスチュワートの定理の証明》
$m,$ $n > 0$ とし, $\triangle\mathrm{ABC}$ の辺 $\mathrm{BC}$ を $m:n$ に内分する点を $\mathrm P$ とおく.
\[ n\mathrm{AB}^2+m\mathrm{AC}^2 = (m+n)\mathrm{AP}^2+n\mathrm{BP}^2+m\mathrm{CP}^2 \quad \cdots [*]\]
が成り立つことを, ベクトルを使って示せ.
(参考: $2021$ 兵庫医科大)
解答例
$m+n = 1$ であるとしても一般性を失わないから, その場合を考える.
$\vec b = \overrightarrow{\mathrm{AB}},$ $\vec c = \overrightarrow{\mathrm{AC}}$ とおく.
このとき, $\overrightarrow{\mathrm{AP}} = n\vec b+m\vec c,$ $\overrightarrow{\mathrm{BP}} = \overrightarrow{\mathrm{AP}}-\overrightarrow{\mathrm{AB}}= m(\vec c-\vec b),$ $\overrightarrow{\mathrm{CP}} = \overrightarrow{\mathrm{AP}}-\overrightarrow{\mathrm{AC}}= n(\vec b-\vec c)$ であるから,
\[\begin{aligned}
&(m+n)|\overrightarrow{\mathrm{AP}}|^2+n|\overrightarrow{\mathrm{BP}}|^2+m|\overrightarrow{\mathrm{CP}}|^2 \\
&= |n\vec b+m\vec c|^2+nm^2|\vec c-\vec b|^2+mn^2|\vec b-\vec c|^2 \\
&= |n\vec b+m\vec c|^2+mn(m+n)|\vec b-\vec c|^2 \\
&= (n^2|\vec b|^2+2mn\vec b\cdot\vec c+m^2|\vec c|^2)+mn(|\vec b|^2-2\vec b\cdot\vec c+|\vec c|^2) \\
&= n(n+m)|\vec b|^2+m(m+n)|\vec c|^2 = n|\overrightarrow{\mathrm{AB}}|^2+m|\overrightarrow{\mathrm{AC}}|^2
\end{aligned}\]
つまり $[*]$ が成り立つ.
第 $1,$ 第 $3,$ 第 $5$ の等号では, $m+n = 1$ であることを使った.
参考
- 等式 $[*],$ および $[*]$ において $m = \mathrm{BP},$ $n = \mathrm{CP}$ として得られる等式 $\mathrm{CP}\cdot\mathrm{BP}^2+\mathrm{BP}\cdot\mathrm{CP}^2 = \mathrm{BC}\cdot (\mathrm{AP}^2+\mathrm{BP}\cdot\mathrm{CP})$ は「スチュワートの定理」(Stewart's theorem) として知られており, 特に $m = n$ の場合は「中線定理」(parallelogram law) としてよく知られている.
- 「スチュワートの定理」の別証明については, 余弦定理による証明 (こちら) と, 距離の公式による証明 (こちら), 複素数による証明 (こちら) も参照されたい.
問題《角の二等分線の傾き》
$a,$ $b$ を $b \neq \pm a$ なる実数とする.
$2$ 直線 $y = ax,$ $y = bx$ のなす角の二等分線の傾き $c$ を $a,$ $b$ で表す公式を, ベクトルの内積の公式から導け.
解答例
$3$ 直線 $y = ax,$ $y = bx,$ $y = cx$ の方向ベクトル $\vec a = (1,a),$ $\vec b = (1,b),$ $\vec c = (1,c)$ について, $\vec a,$ $\vec c$ のなす角の余弦と $\vec b,$ $\vec c$ のなす角の余弦は絶対値が等しいから, ベクトルの内積の公式により
\[\begin{aligned}
\frac{|\vec a\cdot\vec c|}{|\vec a||\vec c|} &= \frac{|\vec b\cdot\vec c|}{|\vec b||\vec c|} \\
\frac{|1+ac|}{\sqrt{1+a^2}\sqrt{1+c^2}} &= \frac{|1+bc|}{\sqrt{1+b^2}\sqrt{1+c^2}} \\
|1+ac|\sqrt{1+b^2} &= |1+bc|\sqrt{1+a^2}
\end{aligned}\]
が成り立つ.
両辺を $2$ 乗すると
\[ (1+ac)^2(1+b^2) = (1+bc)^2(1+a^2) \quad \cdots [\ast ]''\]
よって
\[\begin{aligned}
(1+ac)^2(1+b^2)-(1+bc)^2(1+a^2) &= 0 \\
(a^2-b^2)c^2+2(a-b+ab^2-a^2b)c-a^2+b^2 &= 0 \\
(a+b)(a-b)c^2-2(a-b)(ab-1)c-(a+b)(a-b) &= 0 \\
(a+b)c^2-2(ab-1)c-(a+b) &= 0
\end{aligned}\]
となるから, $2$ 次方程式の解の公式により
\[\begin{aligned}
c &= \frac{ab-1\pm\sqrt{(ab-1)^2+(a+b)^2}}{a+b} \\
&= \frac{ab-1\pm\sqrt{(a^2+1)(b^2+1)}}{a+b}
\end{aligned}\]
が得られる.
参考
問題《正多角形の辺と対角線の長さの平方和》
$n$ を $3$ 以上の整数とする.
点 $\mathrm O$ を中心とする半径 $1$ の円に内接する正 $n$ 角形 $\mathrm P_1\mathrm P_2\cdots\mathrm P_n$ において, 次のことを示せ.
- (1)
- 等式 \[\sum_{k = 1}^n\overrightarrow{\mathrm{OP}_k} = \vec 0\] が成り立つ.
- (2)
- 頂点 $\mathrm P_n$ と他の頂点を結ぶ辺, 対角線の長さの平方和は, \[\sum_{k = 1}^{n-1}\mathrm P_k\mathrm P_n{}^2 = 2n\] である.
- (3A)
- すべての辺, 対角線の長さの平方和は, \[\sum_{i = 1}^{n-1}\sum_{j = i+1}^n\mathrm P_i\mathrm P_j{}^2 = n^2\] である.
- (3B)
- 相異なる長さをもつ辺, 対角線の長さの平方和は, $n$ が奇数のとき \[\sum_{k = 1}^{\frac{n-1}{2}}\mathrm P_k\mathrm P_n{}^2 = n,\] $n$ が偶数のとき \[\sum_{k = 1}^{\frac{n}{2}}\mathrm P_k\mathrm P_n{}^2 = n+2\] である.
解答例
- (1)
- $\angle\mathrm P_k\mathrm O\mathrm P_{k+1} = \dfrac{2\pi}{n}$ は正 $n$ 角形の外角の大きさに等しいから, $k = 1,$ $\cdots,$ $n-1$ の順に $\overrightarrow{\mathrm{OP}_k}$ の終点に $\overrightarrow{\mathrm{OP}_{k+1}}$ の始点を合わせてなぞると正 $n$ 角形が描かれる. つまり, \[\sum_{k = 1}^n\overrightarrow{\mathrm{OP}_k} = \overrightarrow{\mathrm{OO}} = \vec 0 \quad \cdots [1]\] が成り立つ.
- (2)
- $[1]$ により, \[\begin{aligned} \sum_{k = 1}^{n-1}\mathrm P_k\mathrm P_n{}^2 &= \sum_{k = 1}^n\mathrm P_k\mathrm P_n{}^2 \quad (\because\mathrm P_n\mathrm P_n{}^2 = 0) \\ &= \sum_{k = 1}^n|\overrightarrow{\mathrm P_k\mathrm P_n}|^2 = \sum_{k = 1}^n|\overrightarrow{\mathrm{OP}_n}-\overrightarrow{\mathrm{OP}_k}|^2 \\ &= \sum_{k = 1}^n(|\overrightarrow{\mathrm{OP}_n}|^2+|\overrightarrow{\mathrm{OP}_k}|^2-2\overrightarrow{\mathrm{OP}_n}\cdot\overrightarrow{\mathrm{OP}_k}) \\ &= \sum_{k = 1}^n(1+1)-2\overrightarrow{\mathrm{OP}_n}\cdot\sum_{k = 1}^n\overrightarrow{\mathrm{OP}_k} \\ &= 2n-2\overrightarrow{\mathrm{OP}_n}\cdot\vec 0 \quad (\because [1]) \\ &= 2n \quad \cdots [2] \end{aligned}\] である.
- (3A)
- $[2]$ の値は頂点のとり方によらない. これを頂点の個数だけ加えるとすべての辺, 対角線の長さの平方和の $2$ 倍になるから, 求める値は \[\sum_{k = 1}^{n-1}\mathrm P_k\mathrm P_n{}^2 = \frac{n}{2}\sum_{k = 1}^{n-1}\mathrm P_k\mathrm P_n{}^2 = \frac{n}{2}\cdot 2n = n^2\] である.
- (3B)
- $n = 2m+1$ ($m$: 正の整数) のとき. 正 $n$ 角形は頂点 $\mathrm P_n$ と線分 $\mathrm P_m\mathrm P_{m+1}$ の中点を結ぶ直線に関して対称であるから, $[2]$ により, \[\begin{aligned} \sum_{k = 1}^m\mathrm P_k\mathrm P_n{}^2 &= \frac{1}{2}\sum_{k = 1}^{n-1}\mathrm P_k\mathrm P_n{}^2 \\ &= \frac{1}{2}\cdot 2n = n \end{aligned}\] が成り立つ.
- $n = 2m$ ($m$: $2$ 以上の整数) のとき. 正 $n$ 角形は直線 $\mathrm P_n\mathrm P_m$ に関して対称であるから, $[2]$ により, \[\begin{aligned} \sum_{k = 1}^m\mathrm P_k\mathrm P_n{}^2 &= \frac{1}{2}\left(\sum_{k = 1}^{n-1}\mathrm P_k\mathrm P_n{}^2+\mathrm P_n\mathrm P_m{}^2\right) \\ &= \frac{1}{2}\cdot (2n+2^2) = n+2 \end{aligned}\] が成り立つ.
参考
半径 $1$ の球に内接する正 $n$ 面体に対しても, (3A) と同様の等式が成り立つ.
問題《三角形の頂点からの距離の平方和が最小の点》
平面において, $\triangle\mathrm{ABC}$ の $3$ 頂点からの距離の $2$ 乗の和が最小である点は $\triangle\mathrm{ABC}$ の重心であることを示せ.
(参考: $2018$ 九州大)
解答例
$\mathrm A(\vec a),$ $\mathrm B(\vec b),$ $\mathrm C(\vec c)$ とおき, 点 $\mathrm P(\vec p)$ をとる.
このとき,
\[\begin{aligned}
&\mathrm{AP}^2+\mathrm{BP}^2+\mathrm{CP}^2 \\
&= |\overrightarrow{\mathrm{AP}}|^2+|\overrightarrow{\mathrm{BP}}|^2+|\overrightarrow{\mathrm{CP}}|^2 \\
&= |\vec p-\vec a|^2+|\vec p-\vec b|^2+|\vec p-\vec c|^2 \\
&= |\vec p|^2-2\vec p\cdot\vec a+|\vec a|^2+|\vec p|^2-2\vec p\cdot\vec b+|\vec b|^2+|\vec p|^2-2\vec p\cdot\vec c+|\vec c|^2 \\
&= 3|\vec p|^2-2\vec p\cdot (\vec a+\vec b+\vec c)+|\vec a|^2+|\vec b|^2+|\vec c|^2 \\
&= 3\left|\vec p-\frac{\vec a+\vec b+\vec c}{3}\right| ^2-\frac{|\vec a+\vec b+\vec c|^2}{3}+|\vec a|^2+|\vec b|^2+|\vec c|^2 \\
&= 3\left|\vec p-\frac{\vec a+\vec b+\vec c}{3}\right| ^2+\frac{2}{3}(|\vec a|^2\!+\!|\vec b|^2\!+\!|\vec c|^2\!-\!2\vec a\cdot\vec b\!-\!2\vec b\cdot\vec c\!-\!2\vec c\cdot\vec a) \\
&= 3\left|\vec p-\frac{\vec a+\vec b+\vec c}{3}\right| ^2+\frac{|\vec c-\vec b|^2+|\vec a-\vec c|^2+|\vec b-\vec a|^2}{3}
\end{aligned}\]
が成り立つから, この和が最小であるとき点 $\mathrm P$ は $\triangle\mathrm{ABC}$ の重心である (最小値は $\dfrac{\mathrm{BC}^2+\mathrm{CA}^2+\mathrm{AB}^2}{3}$ である).
別解 1
$\mathrm A(a,b),$ $\mathrm B(-c,0),$ $\mathrm C(c,0),$ $\mathrm P(x,y)$ とおく.
このとき,
\[\begin{aligned}
&\mathrm{AP}^2+\mathrm{BP}^2+\mathrm{CP}^2 \\
&= (x-a)^2+(y-b)^2+(x+c)^2+y^2+(x-c)^2+y^2 \\
&= 3x^2-2ax+3y^2-2by+a^2+b^2+2c^2 \\
&= 3\left( x-\frac{a}{3}\right)^2+3\left( y-\frac{b}{3}\right)^2+\frac{2}{3}a^2+\frac{2}{3}b^2+2c^2
\end{aligned}\]
が成り立つから, この和が最小であるとき点 $\mathrm P$ は $\triangle\mathrm{ABC}$ の重心 $\left(\dfrac{a}{3},\dfrac{b}{3}\right)$ である.
別解 2:「スチュワートの定理」を利用
辺 $\mathrm{BC}$ の中点を $\mathrm D,$ $\triangle\mathrm{ABC}$ の重心を $\mathrm G$ とおく.
「スチュワートの定理」(とその特別な場合である「中線定理」) により
\[\begin{aligned}
\mathrm{AP}^2+2\mathrm{DP}^2 &= 3(\mathrm{GP}^2+\mathrm{AG}\cdot\mathrm{GD}), \\
\mathrm{BP}^2+\mathrm{CP}^2 &= 2(\mathrm{BD}^2+\mathrm{DP}^2)
\end{aligned}\]
が成り立つ.
辺々を加えると
\[\mathrm{AP}^2+\mathrm{BP}^2+\mathrm{CP}^2 = 3\mathrm{GP}^2+3\mathrm{AG}\cdot\mathrm{GD}+2\mathrm{BD}^2\]
となるから, この和が最小であるとき点 $\mathrm P$ は $\triangle\mathrm{ABC}$ の重心 $\mathrm G$ である.
参考
一般に, $\triangle\mathrm{ABC}$ において, $l\mathrm{AP}^2+m\mathrm{BP}^2+n\mathrm{CP}^2$ $(l,\ m,\ n > 0)$ は, 点 $\mathrm P$ が $3$ 本の線分 $\mathrm{AD},$ $\mathrm{BE},$ $\mathrm{CF}$ の交点であるとき, 最小値 $\dfrac{mn\mathrm{BC}^2+nl\mathrm{CA}^2+lm\mathrm{AB}^2}{l+m+n}$ をとる.
ただし, 点 $\mathrm D$ は辺 $\mathrm{BC}$ を $n:m$ に内分する点, 点 $\mathrm E$ は辺 $\mathrm{CA}$ を $l:n$ に内分する点, 点 $\mathrm F$ は辺 $\mathrm{AB}$ を $m:l$ に内分する点である (証明は解答例と同様).
問題《四面体の頂点からの距離の平方和が最小の点》
空間において, 四面体 $\mathrm{ABCD}$ の $4$ 頂点からの距離の $2$ 乗の和が最小である点は四面体 $\mathrm{ABCD}$ の重心であることを示せ.
(参考: $2018$ 東北大)
解答例
$\mathrm A(\vec a),$ $\mathrm B(\vec b),$ $\mathrm C(\vec c),$ $\mathrm D(\vec d)$ とおき, 点 $\mathrm P(\vec p)$ をとる.
このとき,
\[\begin{aligned}
&\mathrm{AP}^2+\mathrm{BP}^2+\mathrm{CP}^2+\mathrm{DP}^2 \\
&= |\overrightarrow{\mathrm{AP}}|^2+|\overrightarrow{\mathrm{BP}}|^2+|\overrightarrow{\mathrm{CP}}|^2+|\overrightarrow{\mathrm{DP}}|^2 \\
&= |\vec p-\vec a|^2+|\vec p-\vec b|^2+|\vec p-\vec c|^2+|\vec p-\vec d|^2 \\
&= |\vec p|^2-2\vec p\cdot\vec a+|\vec a|^2+|\vec p|^2-2\vec p\cdot\vec b+|\vec b|^2 \\
&\qquad +|\vec p|^2-2\vec p\cdot\vec c+|\vec c|^2+|\vec p|^2-2\vec p\cdot\vec d+|\vec d|^2 \\
&= 4|\vec p|^2-2\vec p\cdot (\vec a+\vec b+\vec c+\vec d)+|\vec a|^2+|\vec b|^2+|\vec c|^2+|\vec d|^2 \\
&= 4\left|\vec p-\frac{\vec a+\vec b+\vec c+\vec d}{4}\right| ^2 \\
&\qquad -\frac{|\vec a+\vec b+\vec c+\vec d|^2}{4}+|\vec a|^2+|\vec b|^2+|\vec c|^2+|\vec d|^2
\end{aligned}\]
が成り立つから, この値が最小であるとき点 $\mathrm P$ は四面体 $\mathrm{ABCD}$ の重心である.
コーシー=シュワルツの不等式
定理《コーシー=シュワルツの不等式》
平面上, または空間のすべてのベクトル $\vec a,$ $\vec b$ に対して,
\[|\vec a\cdot\vec b| \leqq |\vec a||\vec b|\]
が成り立つ.
等号成立は, $\vec a,$ $\vec b$ の一方が他方の定数倍である場合に限る.
証明
- (i)
- $\vec a$ または $\vec b$ が $\vec 0$ のときは明らか.
- (ii)
- $\vec a,$ $\vec b$ が $\vec 0$ でないとき, $\vec a,$ $\vec b$ のなす角を $\theta$ とおくと, \[\vec a\cdot\vec b = |\vec a||\vec b|\cos\theta\] であるから, \[ -1 \leqq \cos\theta \leqq 1\] の両辺に $|\vec a||\vec b|$ を掛けると, $-|\vec a||\vec b| \leqq \vec a\cdot\vec b \leqq |\vec a||\vec b|,$ つまり $|\vec a\cdot\vec b| \leqq |\vec a||\vec b|$ が得られる.
問題《コーシー=シュワルツの不等式》
$a,$ $b,$ $c,$ $x,$ $y$ を正の数とする.
次のことを示せ.
- (1)
- $(ax+by)^2 \leqq (a^2+b^2)(x^2+y^2)$ が成り立つ.
- (2)
- $a^2+b^2 = c^2$ のとき, $a\sqrt x+b\sqrt y \leqq c\sqrt{x+y}$ が成り立つ.
(参考: $1995$ 東京大)
解答例
- (1)
- ベクトル $\vec p = (a,b),$ $\vec q = (x,y)$ のなす角を $\theta$ とおく. 内積の定義により, \[\vec p\cdot\vec q = |\vec p||\vec q|\cos\theta \leqq |\vec p||\vec q|\] よって \[ ax+by \leqq \sqrt{a^2+b^2}\sqrt{x^2+y^2} \quad \cdots [1]\] が成り立つから, 両辺を $2$ 乗すると \[ (ax+by)^2 \leqq (a^2+b^2)(x^2+y^2)\] が得られる.
- (2)
- $a^2+b^2 = c^2$ つまり $\sqrt{a^2+b^2} = c$ のとき, $[1]$ において $x,$ $y$ をそれぞれ $\sqrt x,$ $\sqrt y$ に置き換えると, \[\begin{aligned} a\sqrt x+b\sqrt y &\leqq \sqrt{a^2+b^2}\sqrt{(\sqrt x)^2+(\sqrt y)^2} \\ &= c\sqrt{x+y} \end{aligned}\] が得られる.
参考
微分法を利用した別証明については, こちらを参照されたい.
問題《ベクトルの三角不等式》
- (1)
- 平面ベクトル (または空間ベクトル) $\vec a,$ $\vec b$ に対して \[ |\vec a|+|\vec b| \geqq |\vec a+\vec b|\] が成り立つことを示せ. また, その等号成立条件を求めよ.
- (2)
- 平面上 (または空間内) の $3$ 点 $\mathrm P,$ $\mathrm P',$ $\mathrm P''$ に対して \[\mathrm P\mathrm P'+\mathrm P'\mathrm P'' \geqq \mathrm P\mathrm P''\] が成り立つことを示せ. また, その等号成立条件を求めよ.
解答例
- (1)
- 左辺と右辺の $2$ 乗はそれぞれ \[\begin{aligned} (|\vec a|+|\vec b|)^2 &= |\vec a|^2+2|\vec a||\vec b|+|\vec b|^2, \\ |\vec a+\vec b|^2 &= (\vec a+\vec b)\cdot (\vec a+\vec b) \\ &= |\vec a|^2+2\vec a\cdot\vec b+|\vec b|^2 \end{aligned}\] であるから, 辺々を引くと \[ (|\vec a|+|\vec b|)^2-|\vec a+\vec b|^2 = 2(|\vec a||\vec b|-\vec a\cdot\vec b) \geqq 0\] が得られる. 最後の不等号は, コーシー=シュワルツの不等式 \[\vec a\cdot\vec b \leqq |\vec a\cdot\vec b| \leqq |\vec a||\vec b|\] から従う. よって, $(|\vec a|+|\vec b|)^2 \geqq |\vec a+\vec b|^2,$ $|\vec a|+|\vec b| \geqq 0,$ $|\vec a+\vec b| \geqq 0$ であるから, \[ |\vec a|+|\vec b| \geqq |\vec a+\vec b|\] が成り立つ. 等号成立は, $\vec a\cdot\vec b = |\vec a||\vec b|$ である場合に限る. これは, $\vec a = \vec 0$ または $\vec b = \vec 0$ または $\vec a,$ $\vec b$ のなす角が $0^\circ$ であることに他ならない.
- (2)
- (1)で示したことから \[ |\overrightarrow{\mathrm P\mathrm P'}|+|\overrightarrow{\mathrm P'\mathrm P''}| \geqq |\overrightarrow{\mathrm P\mathrm P'}+\overrightarrow{\mathrm P'\mathrm P''}| = |\overrightarrow{\mathrm P\mathrm P''}|\] が成り立つので, $\mathrm P\mathrm P'+\mathrm P'\mathrm P'' \geqq \mathrm P\mathrm P''$ が得られる. 等号成立は, $\overrightarrow{\mathrm P\mathrm P'} = \vec 0$ または $\overrightarrow{\mathrm P'\mathrm P''} = \vec 0$ または $\overrightarrow{\mathrm P\mathrm P'},$ $\overrightarrow{\mathrm P'\mathrm P''}$ のなす角が $0^\circ$である場合, つまり $\mathrm P,$ $\mathrm P',$ $\mathrm P''$ がこの順に同一直線上に並ぶ場合に限る.
参考
本問で示した不等式は「三角不等式」(triangle inequality) として知られている.
問題《内積の不等式と三角形のフェルマー点》
- (1)
- 平面上の単位ベクトル $\overrightarrow{e_1},$ $\overrightarrow{e_2},$ $\overrightarrow{e_3}$ が $\overrightarrow{e_1}+\overrightarrow{e_2}+\overrightarrow{e_3} = \vec 0$ を満たすとする. $\overrightarrow{e_1},$ $\overrightarrow{e_2},$ $\overrightarrow{e_3}$ のなす角をそれぞれ求めよ.
- (2)
- すべての平面ベクトル $\vec a\,(\neq \vec 0),$ $\vec p$ に対して \[ |\vec a-\vec p| \geqq |\vec a|-\frac{\vec a}{|\vec a|}\cdot\vec p\] が成り立つことを示せ.
- (3)
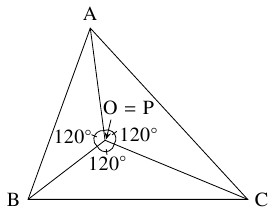
- すべての内角が $120^\circ$ 未満である $\triangle\mathrm{ABC}$ において, 内部の点 $\mathrm P$ から各頂点までの距離の和 $L = |\overrightarrow{\mathrm{PA}}|+|\overrightarrow{\mathrm{PB}}|+|\overrightarrow{\mathrm{PC}}|$ が最小になるとき, 点 $\mathrm P$ はどのような位置にあるか.
(参考: $2000$ 東北大)
解答例
- (1)
- $|\overrightarrow{e_1}+\overrightarrow{e_2}| = |-\overrightarrow{e_3}| = |\overrightarrow{e_3}| = 1$ の両辺を $2$ 乗すると, $|\overrightarrow{e_1}| = |\overrightarrow{e_2}| = 1$ から \[ 1 = |\overrightarrow{e_1}|^2+2\overrightarrow{e_1}\cdot\overrightarrow{e_2}+|\overrightarrow{e_2}|^2 = 2\overrightarrow{e_1}\cdot\overrightarrow{e_2}+2\] つまり $\overrightarrow{e_1}\cdot\overrightarrow{e_2} = -\dfrac{1}{2}$ となるので, $\overrightarrow{e_1}$ と $\overrightarrow{e_2}$ のなす角は $120^\circ$ である. 同様に, $\overrightarrow{e_2}$ と $\overrightarrow{e_3},$ $\overrightarrow{e_3}$ と $\overrightarrow{e_1}$ のなす角は $120^\circ$ である.
- (2)
- コーシー=シュワルツの不等式により, \[\begin{aligned} |\vec a-\vec p| &= \left|\frac{\vec a}{|\vec a|}\right||\vec a-\vec p| \\ &\geqq \left|\frac{\vec a}{|\vec a|}\cdot (\vec a-\vec p)\right| = \left||\vec a|-\dfrac{\vec a}{|\vec a|}\cdot\vec p\right| \quad (\because\vec a\cdot\vec a = |\vec a|^2) \\ &\geqq |\vec a|-\dfrac{\vec a}{|\vec a|}\cdot\vec p \end{aligned}\] が成り立つ. 等号成立は, $\vec a-\vec p$ が $\dfrac{\vec a}{|\vec a|}$ の実数倍,つまり $\vec p$ が $\vec a$ の実数倍であって $|\vec a| \geqq \dfrac{\vec a}{|\vec a|}\cdot\vec p$ である場合に限るので, 実数 $l$ に対して \[\frac{\vec a}{|\vec a|}\cdot l\vec a = l\frac{\vec a\cdot\vec a}{|\vec a|} = l|\vec a|\] が成り立つことから, $\vec p$ が $\vec a$ の $1$ 以下の実数倍である場合に限る.
- (3)
- $\mathrm A,$ $\mathrm B,$ $\mathrm C$ と異なる点 $\mathrm O$ を基点とする位置ベクトルによって
$\mathrm A(\vec a),$ $\mathrm B(\vec b),$ $\mathrm C(\vec c),$ $\mathrm P(\vec p)$ とおく.
(2) で示した不等式から,
\[\begin{aligned}
|\overrightarrow{\mathrm{PA}}| &= |\vec a-\vec p| \geqq |\vec a|-\frac{\vec a}{|\vec a|}\cdot\vec p \quad \cdots [1], \\
|\overrightarrow{\mathrm{PB}}| &= |\vec b-\vec p| \geqq |\vec b|-\frac{\vec b}{|\vec b|}\cdot\vec p \quad \cdots [2], \\
|\overrightarrow{\mathrm{PC}}| &= |\vec c-\vec p| \geqq |\vec c|-\frac{\vec c}{|\vec c|}\cdot\vec p \quad \cdots [3]
\end{aligned}\]
が成り立つ.
辺々を加えると,
\[ L \geqq |\vec a|+|\vec b|+|\vec c|-\left(\frac{\vec a}{|\vec a|}+\frac{\vec b}{|\vec b|}+\frac{\vec c}{|\vec c|}\right)\cdot\vec p\]
が得られる.
$\dfrac{\vec a}{|\vec a|}+\dfrac{\vec b}{|\vec b|}+\dfrac{\vec c}{|\vec c|} = \vec 0$ が成り立つように点 $\mathrm O$ をとり直す.
(1) で示したことから, このような点は $\angle\mathrm{BOC} = \angle\mathrm{COA} = \angle\mathrm{AOB}$ を満たす点として定まる.
しかも, $\triangle\mathrm{ABC}$ の内角に関する条件から, この $\mathrm O$ は $\triangle\mathrm{ABC}$ の内部にとれることに注意する.
このとき,
\[ L \geqq |\vec a|+|\vec b|+|\vec c|\]
が成り立つ.
等号成立は, $[1]$~$[3]$ で等号が成り立つ場合に限る.
これは, $\vec p$ が $\vec a,$ $\vec b,$ $\vec c$ の $1$ 以下の定数倍である場合に限る.
$\vec a,$ $\vec b,$ $\vec c$ は $\vec 0$ でなく互いに平行でないから, これは $\vec p = \vec 0$ の場合である.
ゆえに, $L$ が最小になるような点 $\mathrm P$ は, 上記の点 $\mathrm O$ の位置, つまり $\angle\mathrm{BPC} = \angle\mathrm{CPA} = \angle\mathrm{APB}$ を満たすような位置にある.
参考
- 分岐点を新たに設けてもよいという条件の下で, 与えられたいくつかの点をもれなく結ぶ最短経路を求める問題は, 「最小シュタイナー木問題」(the shortest path problem) と呼ばれ, インフラの建設計画, 電気回路の設計などに現れる素朴で重要な問題である.
- 同一直線上にある $3$ 点を結ぶ最短経路は, 明らかに最も離れた $2$ 点を結ぶ線分である. よって, $3$ 点の「最小シュタイナー木問題」については, $3$ 点が三角形をなす場合が問題になる. 「三角不等式」$\mathrm P\mathrm P'+\mathrm P'\mathrm P'' \geqq \mathrm P\mathrm P''$ を使うと, これは三角形の各頂点までの距離の和が最小になる点を求める問題に帰着できる (詳細は省略).
- $L$ の最小値を与える点 $\mathrm P$ は $\triangle\mathrm{ABC}$ の「フェルマー点」または「トリチェリ点」(Fermat point, Torricelli point) などと呼ばれる (こちらも参照).
- $L$ の最小値 $L_0$ は, $3$ 辺の長さ $a,$ $b,$ $c$ を用いて \[\begin{aligned} L_0 &= \sqrt{\frac{a^2+b^2+c^2+4\sqrt 3S}{2}}, \\ 4S &= \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \end{aligned}\] と表されることが知られている (証明は少し難しい).
ベクトルの垂直条件
定理《ベクトルの垂直条件》
平面または空間において, $\vec 0$ でないベクトル $\vec a,$ $\vec b$ に対し,
\[\vec a\perp\vec b \iff \vec a\cdot\vec b = 0\]
が成り立つ.
問題《ベクトルの大きさの最小値》
ベクトル $\vec a,$ $\vec d$ $(\vec d \neq \vec 0)$ について, $|\vec a+t\vec d|$ が最小になるような実数 $t$ の値を $t_0$ とおく.
- (1)
- $\vec a\cdot\vec d,$ $|\vec d|$ を用いて $t_0$ を表せ.
- (2)
- $\vec d,$ $\vec a+t_0\vec d$ のなす角の大きさを求めよ.
解答例
- (1)
- \[\begin{aligned} |\vec a+t\vec d|^2 &= (\vec a+t\vec d)\cdot (\vec a+t\vec d) \\ &= |\vec a|^2+2t(\vec a\cdot\vec d)+t^2|\vec d|^2 \\ &= |\vec d|^2\left( t+\frac{\vec a\cdot\vec d}{|\vec d|^2}\right) ^2-\frac{(\vec a\cdot\vec d)^2}{|\vec d|^2}+|\vec a|^2 \\ \end{aligned}\] であるから, $|\vec a+t\vec d|^2$ が最小になるような $t$ の値は $t = -\dfrac{\vec a\cdot\vec d}{|\vec d|^2}$ である. $|\vec a+t\vec d| \geqq 0$ であるから, $|\vec a+t\vec d|$ が最小になるような $t$ の値はこれに等しい. つまり, $t_0 = -\dfrac{\vec a\cdot\vec d}{|\vec d|^2}$ である.
- (2)
- \[\begin{aligned} \vec d\cdot (\vec a+t_0\vec d) &= \vec d\cdot\left(\vec a-\dfrac{\vec a\cdot\vec d}{|\vec d|^2}\vec d\right) \\ &= \vec a\cdot\vec d-\vec a\cdot\vec d = 0 \end{aligned}\] であるから, $\vec d,$ $\vec a+t_0\vec d$ のなす角の大きさは $90^\circ$ である.
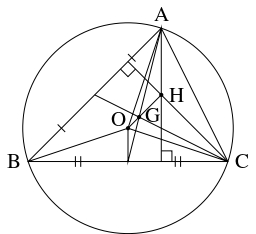
問題《三角形のオイラー線と九点円》
$\triangle\mathrm{ABC}$ の重心を $\mathrm G,$ 外心を $\mathrm O,$ 外接円の半径を $R$ とおく.
次のことを示せ.
ただし, (2) において, $\triangle\mathrm{ABC}$ は正三角形でないとする.
- (1)
- $\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}} = \overrightarrow{\mathrm{OH}}$ を満たす点 $\mathrm H$ は $\triangle\mathrm{ABC}$ の垂心である.
- (2)
- $3$ 点 $\mathrm O,$ $\mathrm G,$ $\mathrm H$ はこの順に同一直線上にあり, $\mathrm{OG}:\mathrm{GH} = 1:2$ である.
- (3)
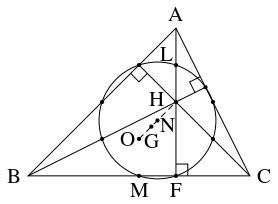
- 直線 $\mathrm{AH},$ $\mathrm{BC}$ の交点 $\mathrm F$ は, 線分 $\mathrm{AH}$ の中点 $\mathrm L,$ 辺 $\mathrm{BC}$ の中点 $\mathrm M$ を直径の両端とし, 線分 $\mathrm{OH}$ の中点 $\mathrm N$ を中心とする半径 $\dfrac{R}{2}$ の円周上にある.
解答例
- (1)
- (i)
- $\triangle\mathrm{ABC}$ が直角三角形であるとき. $\angle\mathrm A = 90^\circ$ であるとしても一般性を失わないから, その場合を考える. このとき, $\triangle\mathrm{ABC}$ の外心 $\mathrm O$ は斜辺 $\mathrm{BC}$ の中点である. よって, $\overrightarrow{\mathrm{OB}} = -\overrightarrow{\mathrm{OC}}$ であるので, 与式から $\overrightarrow{\mathrm{OA}} = \overrightarrow{\mathrm{OH}}$ が成り立つ. したがって, $\mathrm A = \mathrm H$ であるから, 点 $\mathrm H$ は $\triangle\mathrm{ABC}$ の垂心である.
- (ii)
- $\triangle\mathrm{ABC}$ が直角三角形でないとき. $\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}} = \overrightarrow{\mathrm{OH}}$ から, \[\overrightarrow{\mathrm{AH}} = \overrightarrow{\mathrm{OH}}-\overrightarrow{\mathrm{OA}} = \overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}\] である. これと外心の条件 $|\overrightarrow{\mathrm{OA}}| = |\overrightarrow{\mathrm{OB}}| = |\overrightarrow{\mathrm{OC}}|$ から \[\begin{aligned} \overrightarrow{\mathrm{AH}}\cdot\overrightarrow{\mathrm{BC}} &= (\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}})\cdot (\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}) \\ &= |\overrightarrow{\mathrm{OC}}|^2-|\overrightarrow{\mathrm{OB}}|^2 = 0 \end{aligned}\] が成り立つ. 同様に, $\overrightarrow{\mathrm{BH}}\cdot\overrightarrow{\mathrm{CA}} = 0,$ $\overrightarrow{\mathrm{CH}}\cdot\overrightarrow{\mathrm{AB}} = 0$ が成り立つ. これは $\mathrm{AH} \perp \mathrm{BC},$ $\mathrm{BH} \perp \mathrm{CA},$ $\mathrm{CH} \perp \mathrm{AB}$ であることを意味する. したがって, 点 $\mathrm H$ は $\triangle\mathrm{ABC}$ の垂心である.
- (2)
- $\triangle\mathrm{ABC}$ が正三角形でないとき, $\mathrm O \neq \mathrm G$ であることに注意する (こちらを参照). $\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}} = \overrightarrow{\mathrm{OH}}$ から, \[\overrightarrow{\mathrm{OH}} = 3\cdot\dfrac{\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}}{3} = 3\overrightarrow{\mathrm{OG}}\] が成り立つ. よって, $3$ 点 $\mathrm O,$ $\mathrm G,$ $\mathrm H$ はこの順に同一直線上にあり, $\mathrm{OG}:\mathrm{GH} = 1:2$ である.
- (3)
- $\overrightarrow{\mathrm{ON}} = \dfrac{1}{2}\overrightarrow{\mathrm{OH}},$ $\overrightarrow{\mathrm{OL}} = \dfrac{\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OH}}}{2},$ $\overrightarrow{\mathrm{OM}} = \dfrac{\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}}{2}$ から
\[\begin{aligned}
\overrightarrow{\mathrm{NL}} &= \overrightarrow{\mathrm{OL}}-\overrightarrow{\mathrm{ON}} \\
&= \frac{\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OH}}}{2}-\frac{1}{2}\overrightarrow{\mathrm{OH}} = \frac{1}{2}\overrightarrow{\mathrm{OA}}, \\
\overrightarrow{\mathrm{NM}} &= \overrightarrow{\mathrm{OM}}-\overrightarrow{\mathrm{ON}} \\
&= \frac{\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}}{2}-\frac{\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}}{2} = -\frac{1}{2}\overrightarrow{\mathrm{OA}}
\end{aligned}\]
であるので, 点 $\mathrm L,$ $\mathrm M$ は $\mathrm N$ を中心とする半径 $\dfrac{1}{2}|\overrightarrow{\mathrm{OA}}| = \dfrac{R}{2}$ の円周の直径の両端に位置する.
さらに, $\mathrm{LF} \perp \mathrm{FM}$ であるから, 点 $\mathrm F$ もこの円周上にある.
参考
- 三角形において, 外心, 重心, 垂心を通る直線を「オイラー線」(Euler line) と呼ぶ (こちらも参照). ただし, 正三角形に対しては, 外心, 重心, 垂心が一致するため,「オイラー線」は定義されない.
- (3) の結果は頂点 $\mathrm A$ のとり方によらないから, $\triangle\mathrm{ABC}$ の $3$ 辺の中点, 各頂点から対辺またはその延長に下ろした垂線の足, 各頂点と垂心を結ぶ線分の中点, 以上 $9$ 個の点は同一円周上にあり, その中心は外心と垂心を結ぶ線分の中点, 半径は外接円の半径の半分であることがわかる. この円を「九点円」(nine-point circle) と呼ぶ.
問題《三角形に関する直線の直極点》
平面において, 次のことを示せ.
- (1)
- 相異なる $3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ から $\triangle\mathrm{ABC}$ の辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ に下ろした垂線が $1$ 点で交わるためには, \[\mathrm{PB}^2+\mathrm{QC}^2+\mathrm{RA}^2 = \mathrm{PC}^2+\mathrm{QA}^2+\mathrm{RB}^2 \quad \cdots [\ast ]\] の成り立つことが必要十分である.
- (2)
- $\triangle\mathrm{ABC}$ の頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ から直線 $l$ に下ろした垂線の足をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおく. このとき, 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ から辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ に下ろした垂線は $1$ 点で交わる.
解答例
- (1)
- 点 $\mathrm P$ から辺 $\mathrm{BC}$ に下ろした垂線, 点 $\mathrm Q$ から辺 $\mathrm{CA}$ に下ろした垂線の交点を $\mathrm O$ とおく. 点 $\mathrm R$ から辺 $\mathrm{AB}$ に下ろした垂線が点 $\mathrm O$ を通ること, つまり $\mathrm{OR} \perp \mathrm{AB}$ であることと, $[\ast ]$ が同値であることを示せばよい. $\vec a = \overrightarrow{\mathrm{OA}},$ $\vec b = \overrightarrow{\mathrm{OB}},$ $\vec c = \overrightarrow{\mathrm{OC}},$ $\vec p = \overrightarrow{\mathrm{OP}},$ $\vec q = \overrightarrow{\mathrm{OQ}},$ $\vec r = \overrightarrow{\mathrm{OR}}$ とおく. $\mathrm{OP} \perp \mathrm{BC}$ つまり $\overrightarrow{\mathrm{OP}} \perp \overrightarrow{\mathrm{BC}}$ から \[ (\vec c-\vec b)\vec p = 0 \quad \cdots [1]\] が成り立つ. 同様に, $\mathrm{OQ} \perp \mathrm{CA}$ から \[ (\vec a-\vec c)\cdot\vec q = 0 \quad \cdots [2]\] が成り立つ. \[\begin{aligned} &(\mathrm{PB}^2+\mathrm{QC}^2+\mathrm{RA}^2)-(\mathrm{PC}^2+\mathrm{QA}^2+\mathrm{RB}^2) \\ &= |\vec b-\vec p|^2\!+\!|\vec c-\vec q|^2\!+\!|\vec a-\vec r|^2\!-\!|\vec c-\vec p|^2\!-\!|\vec a-\vec q|^2\!-\!|\vec b-\vec r|^2 \\ &= -2\vec b\cdot\vec p-2\vec c\cdot\vec q-2\vec a\cdot\vec r+2\vec c\cdot\vec p+2\vec a\cdot\vec q+2\vec b\cdot\vec r \\ &= 2(\vec c-\vec b)\cdot\vec p+2(\vec a-\vec c)\cdot\vec q+2(\vec b-\vec a)\cdot\vec r \\ &= 2(\vec b-\vec a)\cdot\vec r \quad (\because [1],\ [2]) \end{aligned}\] であるから, \[\mathrm{OR} \perp \mathrm{AB} \iff (\vec b-\vec a)\cdot\vec r = 0 \iff [\ast ]\] が成り立つ.
- (2)
- 三平方の定理により \[\begin{aligned} &= \mathrm{PB}^2+\mathrm{QC}^2+\mathrm{RA}^2-\mathrm{PC}^2+\mathrm{QA}^2+\mathrm{RB}^2 \\ &= (\mathrm{PQ}^2+\mathrm{BQ}^2)+(\mathrm{QR}^2+\mathrm{CR}^2)+(\mathrm{RP}^2+\mathrm{AP}^2) \\ &\qquad -(\mathrm{RP}^2+\mathrm{CR}^2)+(\mathrm{PQ}^2+\mathrm{AP}^2)+(\mathrm{QR}^2+\mathrm{BQ}^2) \\ &= 0 \end{aligned}\] が成り立つから, (1) により点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ から辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ に下ろした垂線は $1$ 点で交わる.
参考
- (2) の $3$ 本の垂線の交点を直線 $l$ の「直極点」(orthopole) または「ノイベルク点」(Neuberg point) と呼ぶ.
- 外心が $\mathrm O,$ 内心が $\mathrm I,$ $\angle\mathrm A_k$ 内の傍心が $\mathrm I_k$ $(k = 1,\ 2,\ 3)$ である $\triangle\mathrm A_1\mathrm A_2\mathrm A_3$ において,「九点円」(こちらを参照) は, 内接円 $\mathrm I,$ 傍接円 $\mathrm I_k$ とそれぞれ直線 $\mathrm{OI},$ $\mathrm{OI}_k$ の「直極点」で接することが知られている.
問題《グラム=シュミットの正規直交化法》
$\overrightarrow{a_1},$ $\overrightarrow{a_2},$ $\overrightarrow{a_3}$ を $\vec 0$ でなく互いに平行でない空間ベクトルとし,
\[\begin{aligned}
\overrightarrow{u_1} &= \frac{\overrightarrow{a_1}}{|\overrightarrow{a_1}|}, \\
\overrightarrow{v_2} &= \overrightarrow{a_2}-(\overrightarrow{a_2}\cdot\overrightarrow{u_1})\,\overrightarrow{u_1}, \quad \overrightarrow{u_2} = \frac{\overrightarrow{v_2}}{|\overrightarrow{v_2}|}, \\
\overrightarrow{v_2} &= \overrightarrow{a_3}-(\overrightarrow{a_3}\cdot\overrightarrow{u_1})\,\overrightarrow{u_1}-(\overrightarrow{a_3}\cdot\overrightarrow{u_2})\,\overrightarrow{u_2}, \quad \overrightarrow{u_3} = \frac{\overrightarrow{v_3}}{|\overrightarrow{v_3}|}
\end{aligned}\]
とする.
次のことを示せ.
- (1)
- $\overrightarrow{u_1},$ $\overrightarrow{u_2},$ $\overrightarrow{u_3}$ は $\vec 0$ でない.
- (2)
- $\overrightarrow{u_1},$ $\overrightarrow{u_2},$ $\overrightarrow{u_3}$ は互いに直交する.
解答例
- (1)
- $\overrightarrow{a_1} = \overrightarrow{\mathrm{OA}_1},$ $\overrightarrow{a_2} = \overrightarrow{\mathrm{OA}_2},$ $\overrightarrow{a_3} = \overrightarrow{\mathrm{OA}_3},$ $\overrightarrow{u_1} = \overrightarrow{\mathrm{OU}_1},$ $\overrightarrow{u_2} = \overrightarrow{\mathrm{OU}_2}$ とする.
- $\overrightarrow{a_1} \neq \vec 0$ から, $\overrightarrow{u_1} \neq \vec 0$ である.
- $\mathrm A_2$ は直線 $\mathrm{OA}_1$ 上になく, 直線 $\mathrm{OA}_1$ と直線 $\mathrm{OU}_1$ は一致するから, $\overrightarrow{v_2} \neq \vec 0$ したがって $\overrightarrow{u_2} \neq \vec 0$ である.
- $\mathrm A_3$ は平面 $\mathrm{OA}_1\mathrm A_2$ 上になく, 平面 $\mathrm{OA}_1\mathrm A_2$ と平面 $\mathrm{OU}_1\mathrm U_2$ は一致するから, $\overrightarrow{v_3} \neq \vec 0$ したがって $\overrightarrow{u_3} \neq \vec 0$ である.
- (2)
- $\overrightarrow{u_1},$ $\overrightarrow{u_2},$ $\overrightarrow{u_3}$ の内積は \[\begin{aligned} \overrightarrow{u_1}\cdot\overrightarrow{u_2} &= \frac{\overrightarrow{u_1}\cdot\overrightarrow{v_2}}{|\overrightarrow{v_2}|} \\ &= \frac{\overrightarrow{u_1}\cdot\overrightarrow{a_2}-(\overrightarrow{a_2}\cdot\overrightarrow{u_1})|\overrightarrow{u_1}|^2}{|\overrightarrow{v_2}|} \\ &= \frac{\overrightarrow{u_1}\cdot\overrightarrow{a_2}-\overrightarrow{a_2}\cdot\overrightarrow{u_1}}{|\overrightarrow{v_2}|} \quad (\because |\overrightarrow{u_1}| = 1) \\ &= 0, \\ \overrightarrow{u_1}\cdot\overrightarrow{u_3} &= \frac{\overrightarrow{u_1}\cdot\overrightarrow{v_3}}{|\overrightarrow{v_3}|} \\ &= \frac{\overrightarrow{u_1}\cdot\overrightarrow{a_3}-(\overrightarrow{a_3}\cdot\overrightarrow{u_1})|\overrightarrow{u_1}|^2-(\overrightarrow{a_3}\cdot\overrightarrow{u_2})\,(\overrightarrow{u_1}\cdot\overrightarrow{u_2})}{|\overrightarrow{v_3}|} \\ &= \frac{\overrightarrow{u_1}\cdot\overrightarrow{a_3}-\overrightarrow{a_3}\cdot\overrightarrow{u_1}}{|\overrightarrow{v_3}|} \quad (\because |\overrightarrow{u_1}| = 1,\ \overrightarrow{u_1}\cdot\overrightarrow{u_2} = 0) \\ &= 0, \\ \overrightarrow{u_2}\cdot\overrightarrow{u_3} &= \frac{\overrightarrow{u_2}\cdot\overrightarrow{v_3}}{|\overrightarrow{v_3}|} \\ &= \frac{\overrightarrow{u_2}\cdot\overrightarrow{a_3}-(\overrightarrow{a_3}\cdot\overrightarrow{u_1})\,(\overrightarrow{u_2}\cdot\overrightarrow{u_1})-(\overrightarrow{a_3}\cdot\overrightarrow{u_2})|\overrightarrow{u_2}|^2}{|\overrightarrow{v_3}|} \\ &= \frac{\overrightarrow{u_2}\cdot\overrightarrow{a_3}-\overrightarrow{a_3}\cdot\overrightarrow{u_2}}{|\overrightarrow{v_3}|} \quad (\because\overrightarrow{u_1}\cdot\overrightarrow{u_2} = 0,\ |\overrightarrow{u_2}| = 1) \\ &= 0 \end{aligned}\] であるから, $\overrightarrow{u_1},$ $\overrightarrow{u_2},$ $\overrightarrow{u_3}$ は互いに直交する.
参考
互いに直交する単位ベクトルの集合を「正規直交系」と呼ぶ.
本問のように「正規直交系」を作るアルゴリズムを「グラム=シュミットの正規直交化法」(Gram–Schmidt orthonormalization) と呼ぶ.
問題《四面体のモンジュ点》
四面体 $\mathrm{ABCD}$ の外接球の中心を $\mathrm O$ とおく.
$\vec a = \overrightarrow{\mathrm{OA}},$ $\vec b = \overrightarrow{\mathrm{OB}},$ $\vec c = \overrightarrow{\mathrm{OC}},$ $\vec d = \overrightarrow{\mathrm{OD}}$ とおき,
$\overrightarrow{\mathrm{OM}} = \dfrac{\vec a+\vec b+\vec c+\vec d}{2}$ で定まる点 $\mathrm M$ をとる.
辺 $\mathrm{AB}$ の中点 $\mathrm L$ について, $\mathrm{LM} \perp \mathrm{CD}$ であることを示せ.
解答例
\[\begin{aligned}
&\overrightarrow{\mathrm{LM}} = \overrightarrow{\mathrm{OM}}-\overrightarrow{\mathrm{OL}} = \frac{\vec a+\vec b+\vec c+\vec d}{2}-\frac{\vec a+\vec b}{2} = \frac{\vec c+\vec d}{2}
\end{aligned}\]
であるから,
\[\overrightarrow{\mathrm{LM}}\cdot\overrightarrow{\mathrm{CD}} = \frac{\vec c+\vec d}{2}\cdot (\vec d-\vec c) = \frac{|\vec d|^2-|\vec c|^2}{2} = 0\]
が成り立つ.
よって, $\mathrm{LM} \perp \mathrm{CD}$ である.
参考
本問において, 点 $\mathrm M$ は, 辺 $\mathrm{AB}$ の中点を通って辺 $\mathrm{CD}$ に垂直な平面上にある.
この辺 $\mathrm{AB}$ と対辺 $\mathrm{CD}$ の選び方は任意だから,
四面体 $\mathrm{ABCD}$ の各辺の中点を通って対辺に垂直な $6$ 枚の平面は $1$ 点 $\mathrm M$ で交わる.
この点 $\mathrm M$ を四面体 $\mathrm{ABCD}$ の「モンジュ点」(Monge point) と呼ぶ.
外心 $\mathrm O,$ 重心 $\mathrm G$ について
\[\overrightarrow{\mathrm{OM}} = 2\overrightarrow{\mathrm{OG}}\]
であるから, $\mathrm O,$ $\mathrm G,$ $\mathrm M$ は一直線上にあり, $\mathrm{OG}:\mathrm{GM} = 1:1$ である.
$\mathrm O \neq \mathrm G$ のとき, $\mathrm O,$ $\mathrm G,$ $\mathrm M$ を通る直線を四面体 $\mathrm{ABCD}$ の「オイラー線」(Euler line) と呼ぶ.
問題《四面体の垂心の存在条件》
四面体 $\mathrm{ABCD}$ において,
- (i)
- 各頂点から対面に下ろした垂線が $1$ 点 $\mathrm H$ で交わる
- (ii)
- 向かい合うどの $2$ 辺も互いに垂直である
解答例
(i) $\Longrightarrow$ (ii): 略.
(ii) $\Longrightarrow$ (i): (ii) を仮定する. \[\begin{aligned} &2\overrightarrow{\mathrm{AH}}\cdot\overrightarrow{\mathrm{BC}} \\ &= 2(\overrightarrow{\mathrm{OH}}-\overrightarrow{\mathrm{OA}})\cdot (\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}) \\ &= (-\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OD}})\cdot (\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}) \\ &= (\overrightarrow{\mathrm{OD}}-\overrightarrow{\mathrm{OA}})\cdot (\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}})+(\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OB}})\cdot (\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}) \\ &= \overrightarrow{\mathrm{AD}}\cdot\overrightarrow{\mathrm{BC}}+|\overrightarrow{\mathrm{OC}}|^2-|\overrightarrow{\mathrm{OB}}|^2 \\ &= 0 \quad (\because\mathrm{AD}\perp\mathrm{BC},\ \mathrm{OB} = \mathrm{OC}) \end{aligned}\] であるから, $\mathrm{AH} \perp \mathrm{BC}$ が成り立つ. 同様に $\mathrm{AH} \perp \mathrm{BD}$ も成り立つから, $\mathrm{AH}$ と平面 $\mathrm{BCD}$ は直交している. 同様に $\mathrm{BH}$ と平面 $\mathrm{ACD},$ $\mathrm{CH}$ と平面 $\mathrm{ABD},$ $\mathrm{DH}$ と平面 $\mathrm{ABC}$ は直交しているから, 点 $\mathrm H$ は各頂点から対面に下ろした垂線の交点である.
(ii) $\Longrightarrow$ (i): (ii) を仮定する. \[\begin{aligned} &2\overrightarrow{\mathrm{AH}}\cdot\overrightarrow{\mathrm{BC}} \\ &= 2(\overrightarrow{\mathrm{OH}}-\overrightarrow{\mathrm{OA}})\cdot (\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}) \\ &= (-\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OD}})\cdot (\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}) \\ &= (\overrightarrow{\mathrm{OD}}-\overrightarrow{\mathrm{OA}})\cdot (\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}})+(\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OB}})\cdot (\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}) \\ &= \overrightarrow{\mathrm{AD}}\cdot\overrightarrow{\mathrm{BC}}+|\overrightarrow{\mathrm{OC}}|^2-|\overrightarrow{\mathrm{OB}}|^2 \\ &= 0 \quad (\because\mathrm{AD}\perp\mathrm{BC},\ \mathrm{OB} = \mathrm{OC}) \end{aligned}\] であるから, $\mathrm{AH} \perp \mathrm{BC}$ が成り立つ. 同様に $\mathrm{AH} \perp \mathrm{BD}$ も成り立つから, $\mathrm{AH}$ と平面 $\mathrm{BCD}$ は直交している. 同様に $\mathrm{BH}$ と平面 $\mathrm{ACD},$ $\mathrm{CH}$ と平面 $\mathrm{ABD},$ $\mathrm{DH}$ と平面 $\mathrm{ABC}$ は直交しているから, 点 $\mathrm H$ は各頂点から対面に下ろした垂線の交点である.
参考
- 四面体 $\mathrm{OABC}$ において, 向かい合うどの $2$ 辺も互いに垂直であることと, $4$ 頂点から対面に下ろした垂線の足が $1$ 点で交わることは, 同値である. このような四面体は「直稜四面体」「直辺四面体」または「垂心四面体」(orthogonal tetrahedron, perpendicular tetrahedron, orthocentric tetrahedron) と呼ばれる.
- 四面体 $\mathrm{ABCD}$ が「直稜四面体」であるための必要十分条件は \[\mathrm{AB}^2+\mathrm{CD}^2 = \mathrm{AC}^2+\mathrm{BD}^2 = \mathrm{AD}^2+\mathrm{BC}^2\] であることが知られている.
- 「直稜四面体」において, 各頂点から対面に下ろした垂線 $4$ 本の交点を, 四面体の「垂心」と呼ぶ. この「垂心」は「モンジュ点」(こちらを参照) に一致することが知られている.
三角形の面積
定理《ベクトルと三角形の面積》
$\triangle\mathrm{OPQ}$ において, $\overrightarrow{\mathrm{OP}} = (a,b),$ $\overrightarrow{\mathrm{OQ}} = (c,d)$ であるとき,
\[\begin{aligned}
\triangle\mathrm{OPQ} &= \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OP}}|^2|\overrightarrow{\mathrm{OQ}}|^2-({\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}})^2} \\
&= \frac{1}{2}|ad-bc|
\end{aligned}\]
が成り立つ.
問題《三角形の面積の公式》
上記の公式を示せ.
解答例
- (1)
- 三角形の面積の公式をベクトルの内積を使って変形すると, \[\begin{aligned} \triangle\mathrm{OPQ} &= \frac{1}{2}\mathrm{OP}\cdot\mathrm{OQ}\sin\angle\mathrm{POQ} \\ &= \frac{1}{2}|\overrightarrow{\mathrm{OP}}||\overrightarrow{\mathrm{OQ}}|\sqrt{1-\cos ^2\angle\mathrm{POQ}} \\ &= \frac{1}{2}|\overrightarrow{\mathrm{OP}}||\overrightarrow{\mathrm{OQ}}|\sqrt{1-\left(\frac{\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}}{|\overrightarrow{\mathrm{OP}}||\overrightarrow{\mathrm{OQ}}|}\right) ^2} \\ &= \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OP}}|^2|\overrightarrow{\mathrm{OQ}}|^2-({\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}})^2} \quad \cdots [1] \end{aligned}\] となる.
- (2)
- $\overrightarrow{\mathrm{OP}} = (a,b),$ $\overrightarrow{\mathrm{OQ}} = (c,d)$ のとき, $[1]$ により, \[\begin{aligned} \triangle\mathrm{OPQ} &= \frac{1}{2}\sqrt{(a^2+b^2)(c^2+d^2)-(ac+bd)^2} \\ &= \frac{1}{2}\sqrt{(ad-bc)^2} = \frac{1}{2}|ad-bc| \end{aligned}\] が成り立つ.
参考
別証明については, こちらを参照されたい.
問題《三角形の面積のベクトルの内積による表示》
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $\vec a = \overrightarrow{\mathrm{BC}},$ $\vec b = \overrightarrow{\mathrm{CA}},$ $\vec c = \overrightarrow{\mathrm{AB}},$ $p = -\vec b\cdot\vec c,$ $q = -\vec c\cdot\vec a,$ $r = -\vec a\cdot\vec b$ とおく.
- (1)
- $q+r,$ $r+p,$ $p+q \geqq 0$ であることを示し, $p,$ $q,$ $r$ を用いて $a,$ $b,$ $c$ を表せ.
- (2)
- $p,$ $q,$ $r$ を用いて $\triangle\mathrm{ABC}$ の面積を表せ.
解答例
- (1)
- $\vec a+\vec b+\vec c = \vec 0$ が成り立つから, \[\begin{aligned} |\vec a|^2 &= |\vec b+\vec c|^2 = |\vec b|^2+|\vec c|^2+2\vec b\cdot\vec c \\ a^2 &= b^2+c^2-2p \end{aligned}\] である. 同様に \[ b^2 = c^2+a^2-2q, \quad c^2 = a^2+b^2-2r\] であり, 辺々を加えると \[ 0 = 2a^2-2(q+r), \quad a^2 = q+r\] となるから, $q+r \geqq 0$ であり, \[ a = \sqrt{q+r}\] が成り立つ. 同様に, $r+p,$ $p+q \geqq 0$ であり, \[ b = \sqrt{r+p}, \quad c = \sqrt{p+q}\] が成り立つ.
- (2)
- 前問の結果により, \[\begin{aligned} \triangle\mathrm{ABC} &= \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{AB}}|^2|\overrightarrow{\mathrm{AC}}|^2-(\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}})^2} \\ &= \frac{1}{2}\sqrt{|\vec c|^2|-\vec b|^2-\{\vec c\cdot (-\vec b)\}^2} \\ &= \frac{1}{2}\sqrt{b^2c^2-p^2} \\ &= \frac{1}{2}\sqrt{(r+p)(p+q)-p^2} \\ &= \frac{1}{2}\sqrt{qr+rp+pq} \end{aligned}\] が成り立つ.
問題《等面四面体としての正四面体の特徴付け》
四面体 $\mathrm{OABC}$ が正四面体であるためには,
- (i)
- $4$ つの面の面積がすべて等しい
- (ii)
- $\mathrm{OA} \perp \mathrm{BC},$ $\mathrm{OB} \perp \mathrm{CA},$ $\mathrm{OC} \perp \mathrm{AB}$
(参考: $2003$ 京都大)
解答例
正四面体 $\mathrm{OABC}$ において, $4$ つの面は合同な正三角形であるから面積が等しく, 辺 $\mathrm{BC}$ の中点を $\mathrm M$ とおくと $\mathrm{OM} \perp \mathrm{BC},$ $\mathrm{AM} \perp \mathrm{BC},$ よって (面 $\mathrm{OAM}$) $\perp \mathrm{BC}$ となるから, $\mathrm{OA} \perp \mathrm{BC}$ であり, 同様に $\mathrm{OB} \perp \mathrm{CA},$ $\mathrm{OC} \perp \mathrm{AB}$ である.
逆に, (i), (ii) を満たす四面体 $\mathrm{OABC}$ において, $\vec a = \overrightarrow{\mathrm{OA}},$ $\vec b = \overrightarrow{\mathrm{OB}},$ $\vec c = \overrightarrow{\mathrm{OC}}$ とおく. (ii), つまり $\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{BC}} = 0,$ $\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{CA}} = 0,$ $\overrightarrow{\mathrm{OC}}\cdot\overrightarrow{\mathrm{AB}} = 0$ から, \[\vec a\cdot (\vec c-\vec b) = 0, \quad \vec b\cdot (\vec a-\vec c) = 0, \quad \vec c\cdot (\vec b-\vec a) = 0\] であるので, \[\vec b\cdot\vec c = \vec c\cdot\vec a = \vec a\cdot\vec b\] が成り立つ. さらに, (i), 特に $\triangle\mathrm{OBC} = \triangle\mathrm{OCA} = \triangle\mathrm{OAB}$ であることから, \[\frac{1}{2}\!\sqrt{|\vec b|^2|\vec c|^2\!-\!(\vec b\cdot\vec c)^2} = \frac{1}{2}\!\sqrt{|\vec c|^2|\vec a|^2\!-\!(\vec c\cdot\vec a)^2} = \frac{1}{2}\!\sqrt{|\vec a|^2|\vec b|^2\!-\!(\vec a\cdot\vec b)^2},\] \[ |\vec b|^2|\vec c|^2 = |\vec c|^2|\vec a|^2 = |\vec a|^2|\vec b|^2,\] \[ |\vec a| = |\vec b| = |\vec c|,\] つまり \[\mathrm{OA} = \mathrm{OB} = \mathrm{OC}\] である. 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ を始点とするベクトルで考えると \[\mathrm{AO} = \mathrm{AB} = \mathrm{AC}, \quad \mathrm{BO} = \mathrm{BC} = \mathrm{BA}, \quad \mathrm{CO} = \mathrm{CA} = \mathrm{CB}\] も得られるから, 四面体 $\mathrm{OABC}$ は正四面体である.
逆に, (i), (ii) を満たす四面体 $\mathrm{OABC}$ において, $\vec a = \overrightarrow{\mathrm{OA}},$ $\vec b = \overrightarrow{\mathrm{OB}},$ $\vec c = \overrightarrow{\mathrm{OC}}$ とおく. (ii), つまり $\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{BC}} = 0,$ $\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{CA}} = 0,$ $\overrightarrow{\mathrm{OC}}\cdot\overrightarrow{\mathrm{AB}} = 0$ から, \[\vec a\cdot (\vec c-\vec b) = 0, \quad \vec b\cdot (\vec a-\vec c) = 0, \quad \vec c\cdot (\vec b-\vec a) = 0\] であるので, \[\vec b\cdot\vec c = \vec c\cdot\vec a = \vec a\cdot\vec b\] が成り立つ. さらに, (i), 特に $\triangle\mathrm{OBC} = \triangle\mathrm{OCA} = \triangle\mathrm{OAB}$ であることから, \[\frac{1}{2}\!\sqrt{|\vec b|^2|\vec c|^2\!-\!(\vec b\cdot\vec c)^2} = \frac{1}{2}\!\sqrt{|\vec c|^2|\vec a|^2\!-\!(\vec c\cdot\vec a)^2} = \frac{1}{2}\!\sqrt{|\vec a|^2|\vec b|^2\!-\!(\vec a\cdot\vec b)^2},\] \[ |\vec b|^2|\vec c|^2 = |\vec c|^2|\vec a|^2 = |\vec a|^2|\vec b|^2,\] \[ |\vec a| = |\vec b| = |\vec c|,\] つまり \[\mathrm{OA} = \mathrm{OB} = \mathrm{OC}\] である. 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ を始点とするベクトルで考えると \[\mathrm{AO} = \mathrm{AB} = \mathrm{AC}, \quad \mathrm{BO} = \mathrm{BC} = \mathrm{BA}, \quad \mathrm{CO} = \mathrm{CA} = \mathrm{CB}\] も得られるから, 四面体 $\mathrm{OABC}$ は正四面体である.
参考
- 四面体において, $4$ つの面が合同であること, $4$ つの面の面積が等しいこと, 重心, 外心, 内心が一致することは, 同値であることが知られている. このような四面体は「等面四面体」(equifacial tetrahedron) と呼ばれる.
- 任意の鋭角三角形 $\mathrm{ABC}$ に対して, 各面が $\triangle\mathrm{ABC}$ と合同な「等面四面体」が存在する (こちらを参照).
- 「等面四面体」の内接球と各面との接点は, その面の外心であることが知られている.
- 四面体 $\mathrm{OABC}$ において, 向かい合うどの $2$ 辺も互いに垂直であることと, $4$ 頂点から対面に下ろした垂線の足が $1$ 点で交わることは, 同値である. このような四面体は「直稜四面体」「直辺四面体」または「垂心四面体」(orthogonal tetrahedron, perpendicular tetrahedron, orthocentric tetrahedron) と呼ばれる (こちらを参照).
問題《ベクトルの外積とスカラー三重積》
空間ベクトル $\vec a = (a_1,a_2,a_3),$ $\vec b = (b_1,b_2,b_3)$ に対して, ベクトル $\vec a\times\vec b$ を
\[\vec a\times\vec b = (a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1)\]
で定める.
$\vec a,$ $\vec b,$ $\vec c$ が $\vec 0$ でなく互いに平行でないとき, 次のことを示せ.
- (1)
- 平行四辺形 $\mathrm{OAFB}$ の面積 $S$ は \[ S = |\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}|\] である. また, $\vec a,$ $\vec b$ のなす角が $\theta$ であるとき, \[ |\vec a\times\vec b| = |\vec a||\vec b|\sin\theta\] が成り立つ.
- (2)
- $\vec a\times\vec b$ と $\vec a,$ $\vec b$ は垂直である.
- (3)
- 平行六面体 $\mathrm{OAFB}$-$\mathrm{CEGD}$ の体積 $V$ は \[ V = |(\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}})\cdot\overrightarrow{\mathrm{OC}}|\] である.
- (4)
- \[ |(\vec a\times\vec b)\cdot\vec c| = |(\vec b\times\vec c)\cdot\vec a| = |(\vec c\times\vec a)\cdot\vec b|\] が成り立つ.
(参考: $2023$ 広島工業大)
解答例
- (1)
- 平行四辺形 $\mathrm{OADB}$ において, $\overrightarrow{\mathrm{OA}} = (a_1,a_2,a_3),$ $\overrightarrow{\mathrm{OB}} = (b_1,b_2,b_3)$ とする. このとき, 面積 $S$ について \[\begin{aligned} S^2 &= (2\triangle\mathrm{OAB})^2 \\ &= |\overrightarrow{\mathrm{OA}}|^2|\overrightarrow{\mathrm{OB}}|^2-(\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}})^2 \\ &= (a_1{}^2\!+\!a_2{}^2\!+\!a_3{}^2)(b_1{}^2\!+\!b_2{}^2\!+\!b_3{}^2)\!-\!(a_1b_1\!+\!a_2b_2\!+\!a_3b_3)^2 \\ &= a_2{}^2b_3{}^2+a_3{}^2b_2{}^2+a_3{}^2b_1{}^2+a_1{}^2b_3{}^2+a_1{}^2b_2{}^2+a_2{}^2b_1{}^2 \\ &\qquad -2a_2a_3b_2b_3-2a_3a_1b_3b_1-2a_1a_2b_1b_2 \\ &= (a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2 \\ &= |\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}|^2 \end{aligned}\] であるから, \[ S = |\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}|\] が成り立つ. よって, $\vec a = \overrightarrow{\mathrm{OA}},$ $\vec b = \overrightarrow{\mathrm{OB}}$ として $\vec a,$ $\vec b$ のなす角を $\theta$ とすると, \[ |\vec a\times\vec b| = |\vec a||\vec b|\sin\theta\] が得られる.
- (2)
- (1) から $\vec a\times\vec b \neq \vec 0$ であり,
\[\begin{aligned}
(\vec a\times\vec b)\cdot \vec a &= a_1a_2b_3-a_1b_2a_3\\
&\quad +b_1a_2a_3-a_1a_2b_3\\
&\quad +a_1b_2a_3-b_1a_2a_3 \\
&= 0, \\
(\vec a\times\vec b)\cdot \vec b &= b_1a_2b_3-b_1b_2a_3\\
&\quad +b_1b_2a_3-a_1b_2b_3 \\
&\quad +a_1b_2b_3-b_1a_2b_3 \\
&= 0
\end{aligned}\]
であるから, $\vec a\times\vec b$ と $\vec a,$ $\vec b$ は垂直である.
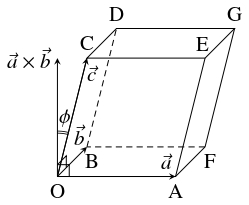
- (3)
- $\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}$ と $\overrightarrow{\mathrm{OC}}$ のなす角を $\phi$ とおく. このとき, 平行六面体 $\mathrm{OAFB}$-$\mathrm{CEGD}$ において, 面 $\mathrm{OAFB}$ を底面と見たときの底面積は $|\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}|,$ 高さは $|\overrightarrow{\mathrm{OC}}\cos\phi|$ であるから, 体積 $V$ は \[\begin{aligned} V &= |\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}||\overrightarrow{\mathrm{OC}}\cos\phi| \\ &= |\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}||\overrightarrow{\mathrm{OC}}||\cos\phi| \\ &= ||\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}||\overrightarrow{\mathrm{OC}}|\cos\phi| \\ &= |(\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}})\cdot\overrightarrow{\mathrm{OC}}| \end{aligned}\] である.
- (4)
- 平行六面体 $\mathrm{OAFB}$-$\mathrm{CEGD}$ において, $\vec a = \overrightarrow{\mathrm{OA}},$ $\vec b = \overrightarrow{\mathrm{OB}},$ $\vec c = \overrightarrow{\mathrm{OC}}$ とおく. 面 $\mathrm{OAFB},$ $\mathrm{OBDC},$ $\mathrm{OCEA}$ のどの面を底面と見ても体積は変わらないから, (3) により \[ |(\vec a\times\vec b)\cdot\vec c| = |(\vec b\times\vec c)\cdot\vec a| = |(\vec c\times\vec a)\cdot\vec b|\] が成り立つ.
参考
- 空間ベクトル $\vec a = (a_1,a_2,a_3),$ $\vec b = (b_1,b_2,b_3)$ に対して, ベクトル \[\vec a\times\vec b = (a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1)\] を $\vec a,$ $\vec b$ の「外積」(cross product) と呼ぶ. 右手の人差し指の指す方を $\vec a$ の向き, 中指の指す方を $\vec b$ の向きに合わせると, 親指の指す方が $\vec a\times\vec b$ の向きである (右手系).
- 空間ベクトル $\vec a,$ $\vec b,$ $\vec c$ に対して, $(\vec a\times\vec b)\cdot\vec c$ を $\vec a,$ $\vec b,$ $\vec c$ の「スカラー三重積」(scalar triple product) と呼ぶ. (4) について, 絶対値を取り除いた等式 \[ (\vec a\times\vec b)\cdot\vec c = (\vec b\times\vec c)\cdot\vec a = (\vec c\times\vec a)\cdot\vec b\] が成り立つ.
- 空間における $\triangle\mathrm{OAB}$ の面積は \[\frac{1}{2}|\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}|\] であり, 四面体 $\mathrm{OABC}$ の体積は \[\frac{1}{6}|(\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}})\cdot\overrightarrow{\mathrm{OC}}|\] である.
