有名問題・定理から学ぶ数学
Well-Known Problems and Theorems in Mathematics
数式を枠からはみ出さずに表示するためには, 画面を横に傾けてください.
角の二等分線に関する不定方程式とペル方程式の解
§1 はじめに
追記: $2$ 直線とそれらのなす角の二等分線の傾きが満たす方程式の有理数解の構造, 一般ペル方程式の解の構造が明らかになり, 本稿の内容と合わせて書かれた論文 “General Pell's equations and angle bisectors between planar lines with rational slopes” (査読あり) がアメリカの数学ジャーナル Integers に掲載されました (2024/12/09).
無料でご覧いただけます.
この記事は「日曜数学 Advent Calendar $2022$」の $20$ 日目の記事として書かれたものです.
※ 一部の記号を $2$ 次体の整数論の専門書寄りに変更しました (2024/12/10).
こんにちは. 廣津孝です. 皆さんとともに数学を通してクリスマスのお祝いができることを大変うれしく思います.
筆者は最近, 高校数学の教材研究を重ねる中で, 平面上の $2$ 直線の傾き $a,$ $b$ とそれらのなす角の二等分線の傾き $c$ がすべて整数になるような $a,$ $b,$ $c$ の値の組合せを決定しました [1]. 内容は中学生にも理解でき, 証明は意欲ある高校生にも理解できる古典的な定理なので (オイラーが発見していたとしてもおかしくないような定理です), この記事でその解説をしたいと思います. 何と, その解にはすべてのネガティブなペル方程式$x^2-dy^2 = -1$ (定義 1) の解が現れます.
今回の研究の発端になったのが, 次の問題です.
$2$ 直線 $y = x,$ $y = 7x$ のなす鋭角の二等分線の傾きを求めよ.
高校数学の問題集でよく出されるものですが, 皆さんは解けるでしょうか…… 答えは $2$ です (解法は命題 1 の証明を参照).
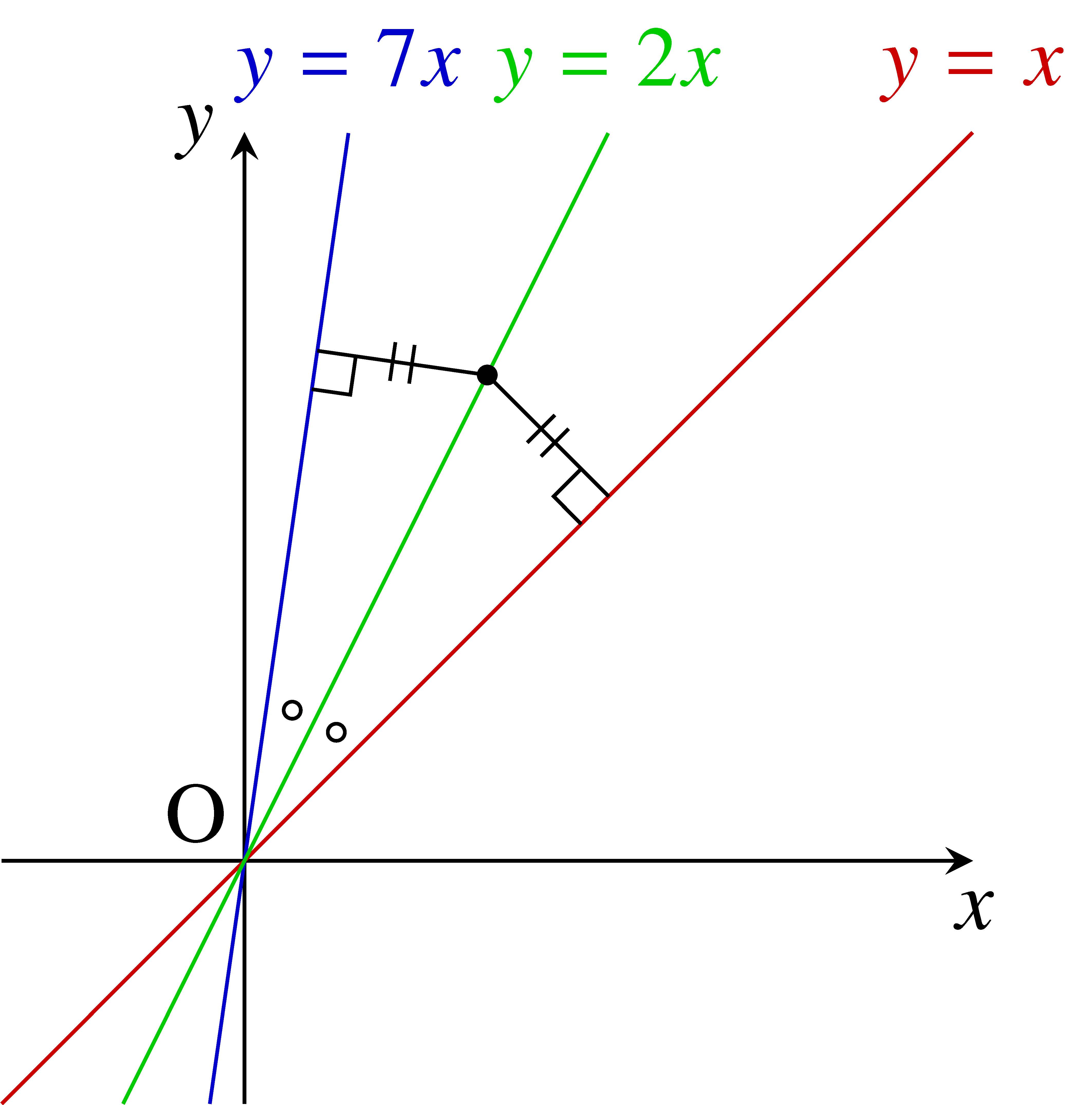
何と $3$ 本の直線の傾きが整数になりました. 数論に興味のある方なら, 次のような疑問が湧いてくることでしょう.
問題 1
どのような整数 $a,$ $b$ $(b \neq \pm a)$ に対して, 傾きが $a,$ $b$ である $2$ 直線のなす角 (鋭角または鈍角) の二等分線の傾き $c$ は整数になるか.
ここで, $2$ 直線のなす角 $\theta$ は $0^\circ \leqq \theta \leqq 180^\circ$ の範囲で考えているのですが, $b = \pm a$ の場合 ($\theta = 0^\circ,$ $90^\circ,$ $180^\circ$ の場合を含む) は, 角の二等分線の傾き $c$ が整数になるのは $(a,b,c) = (a,a,c),$ $(a,-a,0)$ のときに限るので, 既知ということで除外しています.
方眼ノートや描画ソフトを使うとき, 格子点 ($xy$ 平面上の $x$ 座標も $y$ 座標も整数である点) を結んで直線を引くことがよくあると思います. そのようなとき自然に現れるのが, この問題です. つまり, 傾きが有理数の場合まで考えると, 与えられた格子点 $\mathrm O,$ $\mathrm A,$ $\mathrm B$ に対して, $\angle\mathrm{AOB}$ の二等分線が頂点 $\mathrm O$ と他の格子点 $\mathrm C$ を結ぶことで描けるのはいつかという描画の技術上重要な問題になります. ここでは傾きが整数の場合を考えます.
問題 1 を解くために, まず $a,$ $b,$ $c$ がどのような式を満たすかを調べます. $2$ 直線のなす $2$ つの角について, 二等分線は互いに垂直であることに注意しておきます ($2$ 直線のなす $2$ つの角の大きさの和は $180^\circ$ なので, それらの二等分線のなす鋭角の大きさは $180^\circ\div 2 = 90^\circ$).
命題 1
$a,$ $b,$ $c$ $(b \neq \pm a)$ を実数とする.
傾きが $a,$ $b$ の $2$ 直線のなす角の二等分線の傾きが $c,$ $-c^{-1}$ であるとき, $a,$ $b,$ $c$ は
つまり
\[ c = \frac{ab-1\pm\sqrt{(a^2+1)(b^2+1)}}{a+b} \quad \cdots [\star\star ]\]
を満たす.
| $(a-c)^2(b^2+1) = (b-c)^2(a^2+1) \quad \cdots [\star ]$ |
証明
平行移動しても直線の傾きは変わらないので, 直線 $y = cx$ が $2$ 直線 $y = ax,$ $y = bx$ のなす角を二等分する場合に示せば十分です.
このとき, 二等分線 $y = cx$ 上の点 $(t,ct)$ $(t \neq 0)$ と $2$ 直線 $ax-y = 0,$ $bx-y = 0$ の距離は等しいので, 点と直線の距離の公式により
\[\frac{|at-ct|}{\sqrt{a^2+(-1)^2}} = \frac{|bt-ct|}{\sqrt{b^2+(-1)^2}}\]
つまり
\[ |a-c|\sqrt{b^2+1} = |b-c|\sqrt{a^2+1}\]
が成り立ちます.
両辺を $2$ 乗すると,
\[ (a-c)^2(b^2+1) = (b-c)^2(a^2+1) \quad \cdots [\star ]\]
が得られます.
さらに, 両辺を展開して整理すると
\[ (a+b)c^2-2(ab-1)c-(a+b) = 0\]
となるので, $2$ 次方程式の解の公式により
\[\begin{aligned}
c &= \frac{ab-1\pm\sqrt{(ab-1)^2+(a+b)^2}}{a+b} \\
&= \frac{ab-1\pm\sqrt{(a^2+1)(b^2+1)}}{a+b} \quad \cdots [\star\star ]
\end{aligned}\]
が得られます.
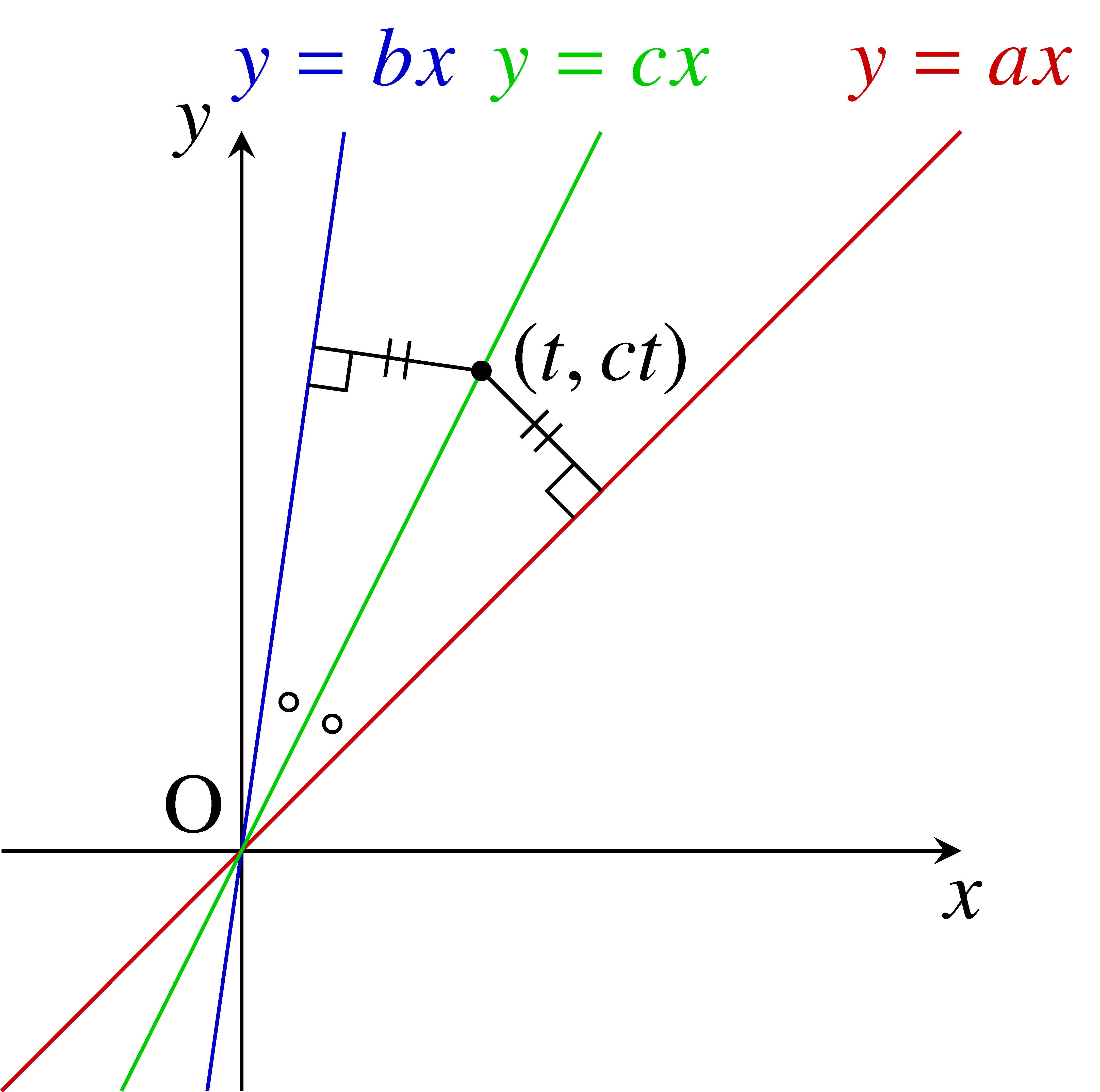
なお, 正接の加法定理を利用する証明, ベクトルの内積を利用する証明もあります.
$[\star ]$ において, $(a,a,c),$ $(a,-a,0)$ の形の解を自明な解と呼ぶことにします. 問題 1 はこの命題により, 次のように言い換えられます.
問題 1'
方程式
\[ (a-c)^2(b^2+1) = (b-c)^2(a^2+1) \quad \cdots [\star ]\]
の非自明な整数解をすべて求めよ.
$[\star ]$ の $a$ に具体的な値を代入して WolframAlpha で計算してみると，次のような整数解が見つかります.
| $a$ | $1$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $7$ | $7$ | $8$ | $\cdots$ | $41$ | $\cdots$ |
| $b$ | $7$ | $-7$ | $38$ | $117$ | $268$ | $515$ | $882$ | $41$ | $1393$ | $-41$ | $2072$ | $\cdots$ | $239$ | $\cdots$ |
| $c$ | $2$ | $3$ | $4$ | $6$ | $8$ | $10$ | $12$ | $12$ | $14$ | $17$ | $16$ | $\cdots$ | $70$ | $\cdots$ |
$c = 2a$ を満たす解が目立ちますが, その他にも解があります. マーカーを引いた数の絶対値 $1,$ $7,$ $41,$ $239,$ $1393$ は, 『オンライン整数列大辞典』で調べてみると, $x^2-2y^2 = -1$ の整数解の $x$ 成分であることが分かります (OEIS: A002315).
省略した $\cdots$ の部分には, $(a,b,c) = (38,682,72)$ という解もあります. この $a,$ $b$ の値も実は別の方程式 $x^2-5y^2 = -1$ の整数解の $x$ 成分です.
$x^2-2y^2 = \pm 1,$ $x^2-5y^2 = \pm 1$ のような方程式が, この記事の主役, ペル方程式です.
定義 1
$d$ を平方数でない正の整数とする.
- (1)
- $x^2-dy^2 = \pm 1$ の形の方程式をペル方程式と呼び, 右辺が $1$ のものをポジティブなペル方程式, 右辺が $-1$ のものをネガティブなペル方程式と呼ぶ.
- (2)
- $|x^2-dy^2| = 1$ の正の整数解 $(x,y) = (x_1,y_1),$ $(x_2,y_2)$ について $x_1 < x_2$ であるとき, $(x_1,y_1)$ は $(x_2,y_2)$ より小さいという.
注意 1
- (1)
- $x^2-dy^2 = 1$ は必ず整数解をもつことが知られています.
- (2)
- $x^2-dy^2 = -1$ が整数解をもつような, $1$ 以外の平方数で割り切れない正の整数 $d$ を小さい順に列挙すると, \[\begin{aligned} &2,\ 5,\ 10,\ 13,\ 17,\ 26,\ 29,\ 37,\ 41,\ 53, \\ &58,\ 61,\ 65,\ 73,\ 74,\ 82,\ 85,\ 89,\ 97, \cdots \end{aligned}\] となります. このような $d$ は $4$ を法として $3$ と合同な素因数をもちません. しかし, この条件は十分ではなく, 例えば $x^2-34y^2 = -1$ は整数解をもちません.
- (3)
- $|x^2-dy^2| = 1$ の正の整数解 $(x,y) = (x_1,y_1),$ $(x_2,y_2)$ について, $x_1 < x_2 \iff y_1 < y_2$ が成り立ちます (証明は割愛).
§2 主定理
問題 1 の解は, ペル方程式の解を用いて, 次のように表されます.
定理 1: 主定理 (廣津 [1, Theorem 1])
ネガティブなペル方程式 $x^2-dy^2 = -1$ が解をもつような, $1$ 以外の平方数で割り切れない正の整数 $d$ に対して, $|x^2-dy^2| = 1$ の $n$ 番目に小さい正の整数解を $(x,y) = (f_n^{(d)},g_n^{(d)})$ とおく.
このとき, $2$ 直線の傾き $a,$ $b$ $(b \neq \pm a)$ とそれらのなす角 (鋭角または鈍角) の二等分線の傾き $c$ がすべて整数になるような $a,$ $b,$ $c$ の値の組, つまり $[\star ]$ の非自明な整数解は, $a,$ $b$ の入れ替えを許せば, 適当な正の整数 $d,$ $m,$ $n$ について
または
の形に表される.
証明は, §3, §4 で準備を行った後, §5 で述べます.
ここでは, 問題 1 にはどのような解があるかを具体例で確認しておきます.
| $(a,b,c) = \pm\left( f_{(2m-1)(2n-1)}^{(d)},f_{(2m-1)(2n+1)}^{(d)},\dfrac{g_{2(2m-1)n}^{(d)}}{g_{2m-1}^{(d)}}\right)$ |
| $(a,b,c) = \pm (f_{2n-1}^{(2)},-f_{2n+1}^{(2)},f_{2n}^{(2)}) $ |
例 1
- (1)
- 各正の整数 $k$ に対して, \[ (a,b) = (k,k(4k^2+3))\] は問題 1 の解で, $y = ax,$ $y = bx$ のなす鋭角の二等分線の傾きは $c = 2k$ です. この $k,$ $k(4k^2+3),$ $2k$ は, それぞれ \[ |x^2−(k^2+1)y^2| = 1\] の正の整数解のうち小さい方から $1$ 番目の解 $(x,y) = (k,1)$ の $x$ 成分, $3$ 番目の解 $(x,y)$ = $(k(4k^2+3),4k^2+1)$ の $x$ 成分, $2$ 番目の解 $(x,y) = (2k^2+1,2k)$ の $y$ 成分 (分母は $1$) です.
- (2)
- $|x^2-2y^2| = 1$ からは, \[\begin{aligned} &(f_1^{(2)},f_3^{(2)}) & &\!\!\!\!\!\!\!\!\!\!\!\!(f_3^{(2)},f_5^{(2)}) & &\!\!\!\!(f_5^{(2)},f_7^{(2)}) \\ &= (1,7), & &\!\!\!\!\!\!\!\!\!\!\!\!= (7,41), & &\!\!\!\!= (41,239),\ \cdots \\ &(f_3^{(2)},f_9^{(2)}) & &\!\!\!\!\!\!\!\!\!\!\!\!(f_9^{(2)},f_{15}^{(2)}) & &\!\!\!\!(f_{15}^{(2)},f_{21}^{(2)}) \\ &= (7,1393), & &\!\!\!\!\!\!\!\!\!\!\!\!= (1393,275807), & &\!\!\!\!= (275807,54608393),\ \cdots \\ &(f_5^{(2)},f_{15}^{(2)}) & & & & \\ &= (41,275807), & &\!\!\!\!\cdots & & \\ &\qquad\vdots \end{aligned}\] や \[\begin{aligned} &(f_1^{(2)},-f_3^{(2)}) & &(f_3^{(2)},-f_5^{(2)}) & &(f_5^{(2)},-f_7^{(2)}) \\ &= (1,-7), & &= (7,-41), & &= (41,-239), \quad \cdots \\ \end{aligned}\] を $(a,b)$ の値とする問題 1 の解が得られます.
- (3)
- $|x^2-5y^2| = 1$ からは, \[\begin{aligned} &(f_1^{(5)},f_3^{(5)}) & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!(f_3^{(5)},f_5^{(5)}) & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!(f_5^{(5)},f_7^{(5)}) \\ &= (2,38), & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= (38,682), & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= (682,12238),\ \cdots \\ &(f_3^{(5)},f_9^{(5)}) & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!(f_9^{(5)},f_{15}^{(5)}) & & \\ &= (38,219602), & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= (219602,1268860318), & &\cdots \\ &(f_5^{(5)},f_{15}^{(5)}) & & & & \\ &= (682,1268860318), & &\!\!\!\!\cdots & & \\ &\qquad\vdots \end{aligned}\] を $(a,b)$ の値とする問題 1 の解が得られます.
$[\star ]$ の非自明な整数解 $(a,b,c)$ には, $a,$ $b$ が同符号とき各 $d$ に対して二重数列のような構造の中に $|x^2-dy^2| = 1$ の解が現れ, $a,$ $b$ が異符号のとき $|x^2-2y^2| = 1$ の解のみが現れるという点が非常に興味深いと思います.
§3 ペル方程式の解が現れる理由
ここでは, 方程式 \[ (a-c)^2(b^2+1) = (b-c)^2(a^2+1) \quad \cdots [\star ]\] の整数解の基本的な性質, 特にペル方程式の解が現れる理由について述べます.
命題 2
- (1)
- $(a,b,c)$ が $[\star ]$ の実数解であるとき, $(a,b,-c^{-1})$ $(c \neq 0),$ $(-a,-b,-c),$ $(b,a,c)$ も $[\star ]$ の実数解である.
- (2)
- $a = 0$ または $b = 0$ のとき, $[\star ]$ は非自明な整数解をもたない.
- (3)
- $[\star ]$ の任意の非自明な整数解 $(a,b,c)$ に対して, $a,$ $b$ が共通のネガティブなペル方程式 $x^2-dy^2 = -1$ の整数解の $x$ 成分になるような, 無平方な ($1$ 以外の平方数で割り切れない) 正の整数 $d$ が存在する.
証明
- (1)
- $(a,b,-c^{-1})$ については, 角の二等分線 $2$ 本が互いに垂直であり, 互いに垂直な $2$ 直線の傾きの積が $-1$ であることから分かります. $(-a,-b,-c),$ $(b,a,c)$ については, 明らかです.
- (2)
- $0$ 以外の整数 $k$ に対して $\sqrt{k^2+1}$ は整数にならない ので, $[\star\star]$ により, $a = 0$ または $b = 0$ のとき $[\star ]$ は非自明な整数解をもちません.
- (3)
- $[\star ]$ の両辺の素因数分解に着目します.
$(a-c)^2,$ $(b-c)^2$ が平方数であることから, 残りの各因数$a^2+1,$ $b^2+1$ の素因数分解における指数が奇数であるような素因数 $p$ ($a^2+1,$ $b^2+1$ が平方数でないことから必ず存在) の組合せは等しいと分かります.
それらの素因数の積を $d$ とおくと,
と表されるので, $a,$ $b$ は $x^2-dy^2 = -1$ の整数解の $x$ 成分になります.$a^2+1 = da_2{}^2, \quad b^2+1 = db_2{}^2$ ($a_2,$ $b_2$: 整数)
§4 ペル方程式の解の性質
本節では, 定理 1 の証明で用いる, ペル方程式の解の性質について述べます. 以下, 正の整数 $d$ が無平方であり ($1$ 以外の平方数で割り切れず), $x^2-dy^2 = -1$ が整数解をもつとして, $|x^2-dy^2| = 1$ の $n$ 番目に小さい正の整数解を $(x,y) = (f_n,g_n)$ とし (定理 1 の $f_n^{(d)},$ $g_n^{(d)}$ の右肩の添え字を省略), $\varepsilon = f_1+g_1\sqrt d$ とおきます ($d \equiv 2\ (\bmod\ 4)$ のとき $\varepsilon$ は $2$ 次体 $\mathbb Q(\sqrt d)$ の基本単数と呼ばれる数です). また, 便宜的に $f_0 = 1,$ $g_0 = 0$ と定めます.
$d = 2$ の場合の $f_n,$ $g_n$ はそれぞれ半ペル=リュカ数, ペル数と呼ばれ, その性質としてよく知られている事実も多いので, 要点のみ解説します.
以下の議論では, 次のような複素共役の類似が重要な役割を果たします.
定義 2
$\alpha = a_1+a_2\sqrt d$ ($a_1,$ $a_2$: 有理数) のとき, $a_1-a_2\sqrt d$ を $\alpha$ と共役な数と呼び, ここでは $\alpha '$ で表す.
命題 3
$\alpha = a_1+a_2\sqrt d,$ $\beta = b_1+b_2\sqrt d$ ($a_1,$ $a_2,$ $b_1,$ $b_2$: 有理数) のとき,
\[ (\alpha\beta )' = \alpha '\beta '\]
が成り立つ.
証明
こちらを参照.
次の $3$ つの命題は, ペル方程式の解の基本的な性質としてよく知られています. 仮定から $\varepsilon\varepsilon ' = -1,$ よって $\varepsilon ^{-1} = -\varepsilon '$ であることに注意します.
命題 4
数列 $\{ f_n\},$ $\{ g_n\}$ は狭義単調増加であり,
\[\varepsilon ^n = f_n+g_n\sqrt d\]
を満たし, 一般項は
と表される.
さらに,
($n$: 正の整数) である.
| $f_n = \dfrac{\varepsilon ^n+\varepsilon '{}^n}{2}, \quad g_n = \dfrac{\varepsilon ^n-\varepsilon '{}^n}{2\sqrt d}$ |
証明
単調増加性は定義と注意 1 (3) から従います.
$(x,y)$ を $|x^2-dy^2| = 1$ の正の整数解とし, 各正の整数 $n$ に対して $\varepsilon ^n = x_n+y_n\sqrt d$ ($x_n,$ $y_n$: 整数) とおきます. $x+y\sqrt d \geqq \varepsilon > 1$ であるので, \[\varepsilon ^n \leqq x+y\sqrt d < \varepsilon ^{n+1}\] を満たす正の整数 $n$ が存在します. 両辺を $\varepsilon ^n$ で割ると, \[ 1 \leqq (x+y\sqrt d)\varepsilon ^{-n} < \varepsilon\] となります. 命題 3 により \[\begin{aligned} \varepsilon ^{-n} &= (\varepsilon ^{-1})^n = (-\varepsilon ')^n = (-1)^n\varepsilon '{}^n = (-1)^n(\varepsilon ^n)' \\ &= (-1)^n(x_n-y_n\sqrt d) \end{aligned}\] であるので, \[\begin{aligned} (x+y\sqrt d)\varepsilon ^{-n} &= (-1)^n(x+y\sqrt d)(x_n-y_n\sqrt d) \\ &= (-1)^n(xx_n-dyy_n)+(-1)^n(-xy_n+yx_n)\sqrt d \end{aligned}\] が成り立ちます. そこで, \[ x_0 = (-1)^n(xx_n-dyy_n), \quad y_0 = (-1)^n(-xy_n+yx_n)\] とおきます. このとき, \[ x_0+y_0\sqrt d = (x+y\sqrt d)\varepsilon ^{-n}, \quad x_0-y_0\sqrt d = (x-y\sqrt d)(-\varepsilon )^n\] となるので, 辺々を掛け合わせると \[ x_0{}^2-dy_0{}^2 = x^2-dy^2 = \pm 1\] となります. これと $\varepsilon$ の最小性により $x_0+y_0\sqrt d = 1$ が成り立つので, $x+y\sqrt d = \varepsilon ^n$ が得られます. よって, $\{ f_n\},$ $\{ g_n\}$ の単調増加性により, \[\varepsilon ^n = f_n+g_n\sqrt d \quad \cdots [1]\] が成り立ちます.
また, $[1]$ の両辺の共役な数をとると $(\varepsilon ^n)' = \varepsilon '{}^n$ により \[\varepsilon '{}^n = f_n-g_n\sqrt d \quad \cdots [1]'\] となるので, $([1]+[1]')\div 2,$ $([1]-[1]')\div 2\sqrt d$ (いわゆる和差算) から \[ f_n = \frac{\varepsilon ^n+\varepsilon '{}^n}{2}, \quad g_n = \frac{\varepsilon ^n-\varepsilon '{}^n}{2\sqrt d}\] が得られます.
最後の主張は, $[1]\times [1]'$ により \[ f_n{}^2-g_n{}^2 = (\varepsilon\varepsilon ')^n = (-1)^n\] であることから従います.
$(x,y)$ を $|x^2-dy^2| = 1$ の正の整数解とし, 各正の整数 $n$ に対して $\varepsilon ^n = x_n+y_n\sqrt d$ ($x_n,$ $y_n$: 整数) とおきます. $x+y\sqrt d \geqq \varepsilon > 1$ であるので, \[\varepsilon ^n \leqq x+y\sqrt d < \varepsilon ^{n+1}\] を満たす正の整数 $n$ が存在します. 両辺を $\varepsilon ^n$ で割ると, \[ 1 \leqq (x+y\sqrt d)\varepsilon ^{-n} < \varepsilon\] となります. 命題 3 により \[\begin{aligned} \varepsilon ^{-n} &= (\varepsilon ^{-1})^n = (-\varepsilon ')^n = (-1)^n\varepsilon '{}^n = (-1)^n(\varepsilon ^n)' \\ &= (-1)^n(x_n-y_n\sqrt d) \end{aligned}\] であるので, \[\begin{aligned} (x+y\sqrt d)\varepsilon ^{-n} &= (-1)^n(x+y\sqrt d)(x_n-y_n\sqrt d) \\ &= (-1)^n(xx_n-dyy_n)+(-1)^n(-xy_n+yx_n)\sqrt d \end{aligned}\] が成り立ちます. そこで, \[ x_0 = (-1)^n(xx_n-dyy_n), \quad y_0 = (-1)^n(-xy_n+yx_n)\] とおきます. このとき, \[ x_0+y_0\sqrt d = (x+y\sqrt d)\varepsilon ^{-n}, \quad x_0-y_0\sqrt d = (x-y\sqrt d)(-\varepsilon )^n\] となるので, 辺々を掛け合わせると \[ x_0{}^2-dy_0{}^2 = x^2-dy^2 = \pm 1\] となります. これと $\varepsilon$ の最小性により $x_0+y_0\sqrt d = 1$ が成り立つので, $x+y\sqrt d = \varepsilon ^n$ が得られます. よって, $\{ f_n\},$ $\{ g_n\}$ の単調増加性により, \[\varepsilon ^n = f_n+g_n\sqrt d \quad \cdots [1]\] が成り立ちます.
また, $[1]$ の両辺の共役な数をとると $(\varepsilon ^n)' = \varepsilon '{}^n$ により \[\varepsilon '{}^n = f_n-g_n\sqrt d \quad \cdots [1]'\] となるので, $([1]+[1]')\div 2,$ $([1]-[1]')\div 2\sqrt d$ (いわゆる和差算) から \[ f_n = \frac{\varepsilon ^n+\varepsilon '{}^n}{2}, \quad g_n = \frac{\varepsilon ^n-\varepsilon '{}^n}{2\sqrt d}\] が得られます.
最後の主張は, $[1]\times [1]'$ により \[ f_n{}^2-g_n{}^2 = (\varepsilon\varepsilon ')^n = (-1)^n\] であることから従います.
命題 5
数列 $\{ f_n\},$ $\{ g_n\}$ は $f_n \geqq g_n,$ $f_1 \geqq \sqrt{d-1}$ を満たす.
証明
$f_n > g_n$ は
\[ f_{2n-1}{}^2-dg_{2n-1}{}^2 = -1, \quad f_{2n}{}^2-dg_{2n}{}^2 = 1\]
よって
\[ f_{2n-1}{}^2 = dg_{2n-1}{}^2-1 \geqq g_{2n-1}{}^2, \quad f_{2n}{}^2 = dg_{2n}{}^2+1 > g_{2n}{}^2\]
であることから従います ($(d-1)g_{2n-1}{}^2 \geqq 1$ に注意).
また,
\[ f_1 = \sqrt{dg_1{}^2-1} \geqq \sqrt{d-1}\]
が成り立ちます.
命題 6
$m,$ $n$ を $m \geqq n$ なる非負整数とする.
- (1)
- 加法公式:
が成り立つ.$f_{m+n} = f_mf_n+dg_mg_n,$ $g_{m+n} = f_mg_n+g_mf_n,$ $f_{m-n} = (-1)^n(f_mf_n-dg_mg_n),$ $g_{m-n} = (-1)^{n+1}(f_mg_n-g_mf_n)$ - (2)
- $2$ 倍公式:
が成り立つ.$f_{2n} = f_n^2+dg_n^2,$ $g_{2n} = 2f_ng_n$
証明
- (1)
- $\varepsilon ^{m+n} = \varepsilon ^m\varepsilon ^n,$ $\varepsilon ^{m-n} = (-1)^n\varepsilon ^m(\varepsilon ^n)'$ の両辺の各因数を数列 $\{ f_n\},$ $\{ g_n\}$ の項を用いて表すと \[\begin{aligned} f_{m+n}+g_{m+n}\sqrt d &= (f_m+g_m\sqrt d)(f_n+g_n\sqrt d) \\ &= (f_mf_n+dg_mg_n)+(f_mg_n+g_mf_n)\sqrt d, \\ f_{m-n}+g_{m-n}\sqrt d &= (f_m+g_m\sqrt d)(f_n-g_n\sqrt d) \\ &= (f_mf_n-dg_mg_n)-(f_mg_n-g_mf_n)\sqrt d \end{aligned}\] となるので, 両辺の係数を比較すると求める等式が得られます ($\sqrt d$ が無理数であることから係数の比較ができます).
- (2)
- (1) の第 $1$ 式, 第 $3$ 式において $m = n$ とすれば得られます.
注意 2
(1) の第 $1$ 式, 第 $2$ 式において $m = 1$ とすると, $\{ f_n\},$ $\{ g_n\}$ の連立漸化式
\[ f_{n+1} = f_nf_1+dg_ng_1, \quad g_{n+1} = f_ng_1+g_nf_1\]
が得られます.
数列 $\{ g_n\}$ における整除関係 ($2$ 数の間の割る, 割り切れるの関係) は添え字の整除関係のみによって決まり, このことはペル数の性質としてよく知られています [2, Theorem 8.4]. 数列 $\{ f_n\}$ における整除関係についても, 同様の性質が成り立ちます.
定理 2 ([2, Theorem 8.4], 廣津 [1, Theorem 3])
$m,$ $n$ を $m \leqq n$ なる正の整数とする.
- (1)
- $(d,f_n) = (f_n,g_n) = 1$ である.
- (2)
- $n$ が $m$ の偶数倍であるならば, $(f_m,f_n) = 1$ である.
- (3)
- 次は同値である.
(P1) $f_n$ は $f_m$ で割り切れる.
(P2) “ $d = 2$ かつ $m = 1$ ” または $n$ は $m$ の奇数倍である. - (4)
- 次は同値である.
(Q1) $g_n$ は $g_m$ で割り切れる.
(Q2) $n$ は $m$ の倍数である.
証明
(1), (3) の (P2) $\Rightarrow$ (P1), (2), (3) の (P1) $\Rightarrow$ (P2), および (1), (4) の順に証明できるのですが, 長いので, 一番難しい (P1) $\Rightarrow$ (P2) の部分だけ証明を紹介します.
$f_n$ が $f_m$ で割り切れるとして, $d \neq 2$ または $m \neq 1$ であるとします. $\{ f_n\}$ の単調増加性と命題 5 により, $f_m > 1$ であることに注意します. $n$ を $m$ で割った商を $q,$ 余りを $r$ とおきます.
ここで, $q$ が偶数であるとして, $q = 2^ek$ ($k$: 奇数) とおきます. 加法公式により, \[ f_n = f_{mq+r} = f_{mq}f_r+dg_{mq}g_r\] です. $2$ 倍公式により $g_{mq} = 2f_{mq/2}g_{mq/2}$ であり, これを合計 $e$ 回繰り返すと $g_{mq}$ は $f_{mk}$ で割り切れることが分かります. さらに (P2) $\Rightarrow$ (P1) により $f_{mk}$ は $f_m$ で割り切れるので, $g_{mq}$ は $f_m$ で割り切れます. (2) により $f_{mq}$ は $f_m$ と互いに素であり, $0 < f_r < f_m$ により $f_r$ は $f_m$ で割り切れないので, $f_n$ は $f_m$ で割り切れません. これは矛盾です.
よって, $q$ は奇数です. 加法公式により, \[ f_n = f_{mq+r} = f_{mq}f_r+dg_{mq}g_r\] です. (P2) $\Rightarrow$ (P1) により $f_{mq}$ は $f_m$ で割り切れるので, $dg_{mq}g_r$ は $f_m$ で割り切れます. $f_m,$ $g_{mq}$ の最大公約数 $g$ は, $f_{mq},$ $g_{mq}$ の公約数なので, $g = 1$ です. よって, $d,$ $g_{mq}$ は $f_m$ と互いに素なので, $g_r$ は $f_m$ で割り切れます. さらに $0 \leqq g_r < g_m < f_m$ であるので $r = 0,$ $n = mq$ であり, $n$ は $m$ で割り切れます.
$f_n$ が $f_m$ で割り切れるとして, $d \neq 2$ または $m \neq 1$ であるとします. $\{ f_n\}$ の単調増加性と命題 5 により, $f_m > 1$ であることに注意します. $n$ を $m$ で割った商を $q,$ 余りを $r$ とおきます.
ここで, $q$ が偶数であるとして, $q = 2^ek$ ($k$: 奇数) とおきます. 加法公式により, \[ f_n = f_{mq+r} = f_{mq}f_r+dg_{mq}g_r\] です. $2$ 倍公式により $g_{mq} = 2f_{mq/2}g_{mq/2}$ であり, これを合計 $e$ 回繰り返すと $g_{mq}$ は $f_{mk}$ で割り切れることが分かります. さらに (P2) $\Rightarrow$ (P1) により $f_{mk}$ は $f_m$ で割り切れるので, $g_{mq}$ は $f_m$ で割り切れます. (2) により $f_{mq}$ は $f_m$ と互いに素であり, $0 < f_r < f_m$ により $f_r$ は $f_m$ で割り切れないので, $f_n$ は $f_m$ で割り切れません. これは矛盾です.
よって, $q$ は奇数です. 加法公式により, \[ f_n = f_{mq+r} = f_{mq}f_r+dg_{mq}g_r\] です. (P2) $\Rightarrow$ (P1) により $f_{mq}$ は $f_m$ で割り切れるので, $dg_{mq}g_r$ は $f_m$ で割り切れます. $f_m,$ $g_{mq}$ の最大公約数 $g$ は, $f_{mq},$ $g_{mq}$ の公約数なので, $g = 1$ です. よって, $d,$ $g_{mq}$ は $f_m$ と互いに素なので, $g_r$ は $f_m$ で割り切れます. さらに $0 \leqq g_r < g_m < f_m$ であるので $r = 0,$ $n = mq$ であり, $n$ は $m$ で割り切れます.
注意 3
定理 1 の証明では, 次の和, 差を積に変換する公式が活躍します.
命題 7
和積の公式: $m > n$ なる正の整数 $m,$ $n$ に対して
が成り立つ.
| $f_{m+n}+f_{m-n} = \begin{cases} 2dg_mg_n & (n \equiv 1 \pmod 2), \\ 2f_mf_n & (n \equiv 0 \pmod 2), \end{cases}$ |
| $f_{m+n}-f_{m-n} = \begin{cases} 2f_mf_n & (n \equiv 1 \pmod 2), \\ 2dg_mg_n & (n \equiv 0 \pmod 2), \end{cases}$ |
| $g_{m+n}+g_{m-n} = \begin{cases} 2f_mg_n & (n \equiv 1 \pmod 2), \\ 2g_mf_n & (n \equiv 0 \pmod 2), \end{cases}$ |
| $g_{m+n}-g_{m-n} = \begin{cases} 2g_mf_n & (n \equiv 1 \pmod 2), \\ 2f_mg_n & (n \equiv 0 \pmod 2) \end{cases}$ |
証明
三角関数の和積の公式の導出と同様です.
注意 4
今は考えていない $x^2-dy^2 = -1$ が解をもたない場合にも, $x^2-dy^2 = 1$ の解について, 本節と類似の定理が成り立ちます (符号などの修正が必要).
§5 証明
定理 1 の証明
方程式
\[ (a-c)^2(b^2+1) = (b-c)^2(a^2+1) \quad \cdots [\star ]\]
の非自明な整数解 $(a,b,c) = (a_1,b_1,c_1)$ について, $a_1,$ $b_1$ は共通のネガティブなペル方程式 $x^2-dy^2 = -1$ ($d$: 無平方な正の整数) の整数解の $x$ 成分であるという性質を思い出します (命題 2 (3)).
$x^2-dy^2 = -1$ が整数解 $(x,y) = (a_1,a_2),$ $(b_1,b_2)$ をもつとき, $[\star ]$ に $a_1{}^2+1 = da_2{}^2,$ $b_1{}^2+1 = db_2{}^2$ を代入して得られる \[ (a_1-c_1)^2db_2{}^2 = (b_1-c_1)^2da_2{}^2\] つまり \[ (a_1-c_1)b_2 = \pm (b_1-c_1)a_2\] を $c_1$ について解くと \[ c_1 = \frac{a_1b_2+b_1a_2}{b_2+a_2},\ \frac{a_1b_2-b_1a_2}{b_2-a_2}\] となるので, $[\star ]$ は有理数解 \[\begin{aligned} \pm\left( a_1,b_1,\frac{a_1b_2+b_1a_2}{b_2+a_2}\right),\ \pm\left( a_1,b_1,\frac{a_1b_2-b_1a_2}{b_2-a_2}\right) \end{aligned}\] をもちます. $a_2,$ $b_2 > 0$ としても一般性を失わないことに注意します. 以下, $0 < a_1 < |b_1|$ であるとして, この有理数解について,
とおき, これらが整数になる条件を考えます.
$\{ f_n\},$ $\{ g_n\}$ を §4 の通りとします.
$a_1,$ $a_2$ と $b_1,$ $b_2$ の絶対値は $\{ f_n\},$ $\{ g_n\}$ の奇数番目の項なので, 次の場合に分けて考えます.
$x^2-dy^2 = -1$ が整数解 $(x,y) = (a_1,a_2),$ $(b_1,b_2)$ をもつとき, $[\star ]$ に $a_1{}^2+1 = da_2{}^2,$ $b_1{}^2+1 = db_2{}^2$ を代入して得られる \[ (a_1-c_1)^2db_2{}^2 = (b_1-c_1)^2da_2{}^2\] つまり \[ (a_1-c_1)b_2 = \pm (b_1-c_1)a_2\] を $c_1$ について解くと \[ c_1 = \frac{a_1b_2+b_1a_2}{b_2+a_2},\ \frac{a_1b_2-b_1a_2}{b_2-a_2}\] となるので, $[\star ]$ は有理数解 \[\begin{aligned} \pm\left( a_1,b_1,\frac{a_1b_2+b_1a_2}{b_2+a_2}\right),\ \pm\left( a_1,b_1,\frac{a_1b_2-b_1a_2}{b_2-a_2}\right) \end{aligned}\] をもちます. $a_2,$ $b_2 > 0$ としても一般性を失わないことに注意します. 以下, $0 < a_1 < |b_1|$ であるとして, この有理数解について,
| $c_+ = \dfrac{a_1b_2+b_1a_2}{b_2+a_2}, \quad c_- = \dfrac{a_1b_2-b_1a_2}{b_2-a_2}$ |
- (i)
$(a_1,a_2) = (f_{2i-1},g_{2i-1}),$ $(b_1,b_2) = (f_{(2i-1)+(4j-2)},g_{(2i-1)+(4j-2)})$ のとき.- 加法公式, 和積の公式, $2$ 倍公式により
であるので, 定理 2 (4) により$c_+ = \dfrac{g_{4(i+j-1)}}{2f_{2(i+j-1)}g_{2j-1}} = \dfrac{g_{2(i+j-1)}}{g_{2j-1}}$
が成り立ちます. このとき, $j = m,$ $2i-1 = (2m-1)(2n-1)$ とおくと, \[ (a_1,b_1,c_+) = \left( f_{(2m-1)(2n-1)},f_{(2m-1)(2n+1)},\frac{g_{2(2m-1)n}}{g_{2m-1}}\right)\] となります.$c_+$ が整数 $\iff$ $g_{2j-1}$ が $g_{2(i+j-1)}$ を割り切る $\iff$ $2j-1$ が $2(i+j-1)$ を割り切る $\iff$ $2j-1$ が $2i-1$ を割り切る - 加法公式, 和積の公式, $2$ 倍公式により \[ c_- = -\frac{g_{4j-2}}{2g_{2(i+j-1)}f_{2j-1}} = -\frac{g_{2j-1}}{g_{2(i+j-1)}}\] であり, 分子より分母の方が大きいので, $c_-$ は整数でありません.
- 加法公式, 和積の公式, $2$ 倍公式により
- (ii)
$(a_1,a_2) = (f_{2i-1},g_{2i-1}),$ $(b_1,b_2) = (-f_{(2i-1)+(4j-2)},g_{(2i-1)+(4j-2)})$ のとき.- 加法公式, 和積の公式, $2$ 倍公式により \[ c_+ = -\frac{g_{4j-2}}{2f_{2(i+j-1)}g_{2j-1}} = -\frac{f_{2j-1}}{f_{2(i+j-1)}}\] であり, 分子より分母の方が大きいので, $c_+$ は整数でありません.
- 加法公式, 和積の公式, $2$ 倍公式により
であるので, 定理 2 (3) により$c_- = \dfrac{g_{4(i+j-1)}}{2g_{2(i+j-1)}f_{2j-1}} = \dfrac{f_{2(i+j-1)}}{f_{2j-1}}$
が成り立ちます (偶数 $2(i+j-1)$ は奇数 $2j-1$ の奇数倍になりません). このとき, $i = n$ とおくと, \[ (a_1,b_1,c_-) = (f_{2n-1}^{(2)},-f_{2n+1}^{(2)},f_{2n}^{(2)})\] となります.$c_-$ が整数 $\iff$ $f_{2j-1}$ が $f_{2(i+j-1)}$ を割り切る $\iff$ $d = 2$ かつ $j = 1$
- (iii)
$(a_1,a_2) = (f_{2i-1},g_{2i-1}),$ $(b_1,b_2) = (f_{(2i-1)+4j},g_{(2i-1)+4j})$ のとき.- 加法公式, 和積の公式, $2$ 倍公式により \[ c_+ = \frac{g_{4(i+j)-2}}{2g_{2(i+j)-1}f_{2j}} = \frac{f_{2(i+j)-1}}{f_{2j}}\] であり, 奇数 $2(i+j)-1$ は偶数 $2j$ の奇数倍にはならないので, 定理 2 (3) により $f_{2(i+j)-1}$ は $f_{2j}$ で割り切れず, $c_+$ は整数でありません.
- 加法公式, 和積の公式, $2$ 倍公式により \[ c_- = -\frac{g_{4j}}{2f_{2(i+j)-1}g_{2j}} = -\frac{f_{2j}}{f_{2(i+j)-1}}\] であり, 分母より分子の方が大きいので, $c_-$ は整数でありません.
- (iv)
$(a_1,a_2) = (f_{2i-1},g_{2i-1}),$ $(b_1,b_2) = (-f_{(2i-1)+4j},g_{(2i-1)+4j})$ のとき.- 加法公式, 和積の公式, $2$ 倍公式により \[ c_+ = -\frac{g_{4j}}{2g_{2(i+j)-1}f_{2j}} = -\frac{g_{2j}}{g_{2(i+j)-1}}\] であり, 分子より分母の方が大きいので, $c_+$ は整数でありません.
- 加法公式, 和積の公式, $2$ 倍公式により \[ c_- = \frac{g_{4(i+j)-2}}{2f_{2(i+j)-1}g_{2j}} = \frac{g_{2(i+j)-1}}{g_{2j}}\] であり, 奇数 $2(i+j)-1$ は偶数 $2j$ の整数倍にならないので, 定理 2 (4) により $g_{2(i+j)-1}$ は $g_{2j}$ で割り切れず, $c_-$ は整数でありません.
§6 おわりに
“角の二等分線の傾き”という素朴な題材にここまで深い数論の定理が眠っていたとは, 非常に驚きでした. $10$ 年ほど前にこの問題に出会ったのですが, そのときはほとんど成果が得られませんでした. 今年この問題に再会し, 命題 2 (3) の性質の発見から次々に研究が進展し, 今回の結果を得ることができました. 傾きが有理数の場合についても興味深い解の構造があるのですが, それはまたの機会に紹介したいと思います. この問題に限らず, また新旧を問わず, 今後も鋭意研究を進めていきたいと思います.
長文にもかかわらず最後まで読んでいただき, ありがとうございました.
参考文献
- [0]
- Takashi Hirotsu, General Pell's equations and angle bisectors between planar lines with rational slopes, Integers, 24 (2024), #A111, 26 pp.
- [1]
- Diophantine equation related to angle bisectors and solutions of Pell's equations, https://arxiv.org/abs/2209.10434
- [2]
- T. Koshy, Pell and Pell-Lucas Numbers with Applications, Springer, New York, 2014.
- [3]
- 『オンライン整数列大辞典』, A002315.
更新履歴
- 2022/12/20
- 公開
- 論文のリンクを修正
- 2022/12/21
- 問題 1 直後の補足説明を修正
- 2022/12/27
- 基本単数に関する説明を修正
- 2023/01/30
- 主定理に非自明解の条件を追加
- 2023/02/02
- 定理 1 の証明で符号に関する説明を追加
- 2024/12/10
- 論文の情報を追加, 記号の改訂
お気づきの点などがありましたら, 以下の連絡先までお願いします.
- 氏 名
- 廣津 孝 (ひろつ たかし)
- (理学博士)
- メール
