本格数学クイズ
手を動かして解くタイプの本格的な数学クイズを収集, 制作しています (対象は高校生以上, 算数クイズや記数法に依存する謎解きは掲載なし).
$1$ 人でじっくり考えて解くのも良し, クイズ大会の早解きで使うのも良しの, 解きごたえのあるクイズを厳選しています.
問題は, 随時追加中です (2023/06/02 掲載開始).
本格数学クイズ (144 問)
代数学
整数論
《素数の無限性》素数が無限に存在することを複数の方法で示せ. →答え
《完全数》$p,$ $q$ を素数とする.
$p\times q$ マスの余白のない方眼紙を罫線に沿って $1$ 個以上の合同な小長方形に分ける.
このような分け方すべてにわたる小長方形の個数の総和がマス目の個数の $2$ 倍に等しいとき, $pq$ の値はいくらか. →答え
《カルキン=ウィルフ木》$\dfrac{1}{1}$ から始めて, 既存の各分数に対して,
①分子はそのままで, もとの分母ともとの分子の和を分母として, 新たな分数を作る,
②分母はそのままで, もとの分母ともとの分子の和を分子として, 新たな分数を作る,
という $2$ つの操作を延々と繰り返す.
このとき, 作られる分数の中に現れない正の有理数は存在するか.
存在する場合にはその例を挙げ, 存在しない場合にはそのことを証明せよ. →答え
《有理数の単位分数の和への分解》$0$ より大きく $1$ より小さいすべての有理数は, 有限個の相異なる正の整数の逆数の和として表すことができるか.
可能な場合には証明を述べ, 不可能な場合には反例を挙げよ.
(ヒント: 分母を分子で割った商が $q$ であるとき, $q+1$ の逆数を $1$ つの項として考えてみよ.) →答え
《フロベニウスの硬貨交換問題》$a,$ $b$ を互いに素な $1$ より大きい整数とする.
$a$ 円硬貨, $b$ 円硬貨のみを使ってちょうど支払えない金額は最大で何円か.
ただし, 各硬貨は何枚使ってもよいが, おつりはもらえないものとする. →答え
《底面積と側面積が等しい整数三角柱》高さが $1$ であり, 残りの辺の長さも整数であって, 底面積と側面積が等しい三角柱は何個あるか. →答え
《底面積と側面積が等しい整数直方体》高さが整数 $z$ であり, 残りの辺の長さも整数であって, 底面積と側面積が等しい直方体は何個あるか. →答え
《ピタゴラスの $3$ つ組に現れる整数》同じ長さのマッチ棒をつなげて直角三角形の枠を作るとき, $1$ 辺に使われるマッチ棒の本数として考えられない整数の最大値はいくらか. →答え
《辺長が整数である格子三角形の面積》方眼紙の罫線 (間隔は $1$) の交点を頂点とする三角形において, 各辺の長さが整数であるならば面積も整数である, という主張は正しいか.
正しければ証明し, 正しくなければ反例を挙げよ. →答え
《平方三角数》正方形 (中実方陣) の形に並べられた複数個の石を, $1$ 段目に $1$ 個, $\cdots,$ $k$ 段目に $k$ 個, $\cdots$ と並べ直していくと, 正三角形の形に余すことなく並べられた.
このとき, 考えられる石の個数として最も少ない個数は何個か. →答え
《出席番号の和》複数人の生徒からなるクラスの全員が出席番号順に $1$ 列に並んでいる.
列の先頭と最後尾からそれぞれ生徒の出席番号の和をとっていったとき, 出席番号が奇数である生徒で $2$ つの和が等しくなった.
この生徒の出席番号として考えられる値は最小でいくらか. →答え
《辺長が等差数列をなすヘロンの三角形》$1$ 辺の長さが $1$ のマッチ棒をつなげて, 鋭角三角形の枠を作る.
各辺で使う本数が等差数列になり, 面積が整数になるようにするとき, 考えられるマッチ棒の本数として最も少ない本数は何本か. →答え
《有理点の距離》$xy$ 平面において $x$ 座標も $y$ 座標も有理数である点を有理点と呼ぶ.
$2$ つの有理点の間の距離が $1,$ $\sqrt 2$ となることはある.
それでは, $2$ つの有理点の間の距離が $\sqrt 3$ となることはあるか. →答え
《平方四角錐数》正方形 (中実方陣) の形に並べられた複数個の球を, $1$ 段目に $1$ 個, $\cdots,$ $k$ 段目に $k$ 個, $\cdots$ となるように積み上げていくと, 正四角錐の形に余すことなく並べられた.
このとき, 考えられる球の個数として最も少ない個数は何個か. →答え
《ハーディー=ラマヌジャンのタクシー数》ラマヌジャンは療養中, ハーディー教授が見舞いに訪れた際に,
“乗ってきたタクシーの番号は $1729$ だった. さして特徴のない数字だったよ”という教授に対して, すぐさま
“そんなことはありません, とても興味深い数字です. それは $2$ つの立方数の和として $2$ 通りに表せる最小の数です”
と答えたという.
$1729$ は立方数の和としてどのように表されるか.
$2$ 通りの表し方を答えよ. →答え
《累乗の差》バレーボール, キンボール ($3$ チームが $1$ つのコートに入って戦う球技) のトーナメント大会がそれぞれ開かれた.
$2$ つの大会の出場チーム数の差は $1$ であり, 各大会でどのチームも $1$ 回戦を戦ったという.
このとき, 各大会の出場チーム数はいくらか. →答え
《累乗の和》三角柱, 四角柱, 五角柱の鉛筆があり, それらの側面には互いに異なる文字が $1$ 個ずつ彫られている.
A さんは三角柱, 四角柱の鉛筆のどちらかをランダムに選び, 三角柱の鉛筆であればそれを $x$ 回, 四角柱の鉛筆であればそれを $y$ 回転がす.
B さんは五角柱の鉛筆を $z$ 回転がす.
A さん, B さんの文字の出方の総数が一致するとき, $x,$ $y,$ $z$ の値はいくらか. →答え
《条件付きフェルマー方程式》$n$ を正の整数とする.
$z \leqq n$ のとき, $x^n+y^n = z^n$ は正の整数解をもつか. →答え
《$3$ 種類のケーキ》同じ大きさの $3$ 種類のホール型のケーキを, $1$ 切れの大きさが種類によって異なるように, それぞれ何等分かに切り分ける.
種類ごとに $1$ 切れずつ集めたときの合計の大きさが, $1$ ホール分未満で, できるだけ大きくなるようにするには, 各ケーキを何等分に切り分ければよいか. →答え
《$1$ 階と $2$ 階の部屋割り》$1$ 階の $m$ 個の部屋には $n$ 人を泊め, $2$ 階の $n$ 個の部屋には $m$ 人を泊めた.
各階で考えられる部屋割りの総数は互いに等しく, 各階の宿泊者数は互いに異なるという.
このとき, 何人の宿泊者がいたか. →答え
数列
《$3$ 辺の長さが等差数列をなす直角三角形》$3$ 辺の長さが等差数列をなすような直角三角形の $3$ 辺の長さの比はいくらか. →答え
《フォンタナの三角形》番号札を A, B に配る.
番号の小さい方から A に $2$ 枚, B に $1$ 枚, $\cdots,$ A に $n+1$ 枚, B に $n$ 枚, $\cdots$ と配っていくとき, $n$ 回目に A に配られる札の番号の和 $S_n$ と B に配られる札の番号の和 $T_n$ の間にはどのような関係があるか. →答え
《カードの番号の積の総和の最大値》A, B がそれぞれ $1$ 番から $n$ 番までの番号札を持っている.
A, B が手札から $1$ 枚ずつ同時に番号札を切っていくとき, 各回の番号の積の総和は最大でいくらになるか. →答え
《ハノイの塔》地面に $3$ 本の棒 A, B, C が立てられており, 棒 A に穴の開いた半径の異なる $n$ 枚の円盤が半径の大きい順に通されている.
- (1)
- すべての円盤を棒 B に移す手数の最小値はいくらか.
- (2)
- 円盤に半径の大きい方から $2$ 枚ごとに白色, 黒色の順に色が塗られているとする.
白色の円盤を棒 B, 黒色の円盤を棒 C に移す手数の最小値はいくらか.
- (2)'
- (2) の最後の状態から棒 B と棒 C の円盤を入れ替える手数の最小値はいくらか.
- (3)
- 円盤に半径の大きい方から $3$ 枚ごとに白色, 灰色, 黒色の順に色が塗られているとする.
白色の円盤を棒 A, 灰色の円盤を棒 B, 黒色の円盤を棒 C に移す手数の最小値はいくらか.
ただし, $1$ 本の棒の最も上にある $1$ 枚を別の棒の最も上に移す操作を $1$ 手と数え, いずれの段階においても小さい円盤の上に大きい円盤は置かないものとする. →答え
《うなぎの寝床での畳の敷き方》ちょうど $n$ 枚の畳が敷けるような長方形のうなぎの寝床に畳を敷く方法は何通りあるか.
ただし, 寝床の縦の長さは畳の長い方の辺の長さに等しく, 横の長さは畳の短い方の辺の長さの $n$ 倍に等しいとする. →答え
《$1$ 段飛ばしを許した階段の登り方》$1$ 歩目は $1$ 段だけ上るとし, $2$ 歩目以降は $1$ 歩で $1$ 段上ることも $2$ 段上ることもできるとするとき, $n$ 段以下の階段を上る方法は全部で何通りあるか. →答え
《フィボナッチ数列の周期性》$F_1 = F_2 = 1,$ $F_{n+2} = F_n+F_{n+1}$ で定まる数列 $\{ F_n\}$ は「フィボナッチ数列」として広く知られている.
どのような $n$ に対して $F_n$ は偶数になるか. →答え
《円卓における席替え》それぞれが動かないか隣に移るように円卓の周りに座った $n$ 人 $(n \geqq 3)$ を並べ替える方法は何通りあるか. →答え
《正四面体の辺上のランダム・ウォーク》正四面体 $\mathrm{ABCD}$ の頂点 $\mathrm A$ にいるアリが $1$ 秒ごとに異なる頂点に等確率で移動していくとき, $n$ 秒後に頂点 $\mathrm A$ にいる確率はいくらか. →答え
《$1$ 人飛ばしの継子立て》出席番号が $1$ 番から $n$ 番までの $n$ 人の生徒が順に $1$ つの輪を作るように並んでいる.
出席番号が $2$ 番の生徒から $1$ 人飛ばしで $1$ 人ずつ輪から抜けていくとき, 最後に残った生徒の出席番号はいくらか.
ただし, $1$ 人飛ばしというルールは, 各時点で残っている生徒に対して考えるものとする. →答え
方程式論
《黄金長方形と超黄金長方形》短辺の長さがともに $1$ である「黄金長方形」,「超黄金長方形」のキャンバスが $1$ 枚ずつある.
$1$ 本につき面積 $1$ の領域が塗れる絵の具でこれらのキャンバスを塗るとき, 何本の絵の具が必要か, 整数で答えよ.
ただし,「黄金長方形」とは, 端から最大の正方形を取り除いて得られる長方形が, もとの長方形と相似になる長方形のことである.
また,「超黄金長方形」とは, $1$ 本の対角線が消えるように, 端から最大の正方形, 最小の長方形を順に取り除いて得られる長方形が, もとの長方形と相似になる長方形のことである. →答え
《カラビの三角形》$\angle\mathrm A$ が鈍角である二等辺三角形 $\mathrm{ABC}$ と, 互いに合同な $2$ つの正方形 $\mathrm{PQRS},$ $\mathrm{ATUV}$ があり, 頂点 $\mathrm P,$ $\mathrm T$ は辺 $\mathrm{AB}$ 上に, 辺 $\mathrm{QR}$ と頂点 $\mathrm U$ は辺 $\mathrm{BC}$ 上に, 頂点 $\mathrm S$ は辺 $\mathrm{AC}$ 上にあるとする.
$\triangle\mathrm{ABC}$ の等辺に対する底辺の長さの比はある $3$ 次方程式を満たす.
その $3$ 次方程式を求めよ. →答え
《奇数次方程式の実数解の存在》実数係数の奇数次の方程式 $f(x) = 0$ は少なくとも $1$ つの実数解をもつ, という主張は正しいか.
正しければ証明し, 正しくなければ反例を挙げよ. →答え
《合比の理》昨年, A 部と B 部の人数比は C 部と D 部の人数比と同じであった.
今年は, A 部に昨年の B 部と同じ人数が増え, B 部の人数は変わらず, C 部に昨年の D 部と同じ人数が増え, D 部の人数は変わらなかった.
このとき, 今年の A 部と B 部の人数比, C 部と D 部の人数比についてどのようなことが言えるか. →答え
《$3$ 数の比》A, B, C の $3$ 人が $1$ 回ずつ輪投げをして, 全員無得点ではなく, A の得点は B の $p$ 倍, B の得点は C の $q$ 倍, C の得点は A の $r$ 倍になった.
このとき, A, B, C の得点の比は何対何対何になるか. →答え
解析学
極限
《方眼の中の正方形》$n\times n$ マスの方眼の罫線に沿って描かれた正方形がマス目全体に占める面積の割合として見込まれる値は, $n$ が大きくなるにつれてどのような値に近づいていくか. →答え
《方眼の中の長方形》$n\times n$ マスの方眼の罫線に沿って描かれた長方形がマス目全体に占める面積の割合として見込まれる値は, $n$ が大きくなるにつれてどのような値に近づいていくか. →答え
《長方形の辺長の比の極限値》正方形の $1$ 辺に, それと $1$ 辺の長さが等しい正方形の辺を貼り合わせて長方形を作る.
その長い方の辺に, それと $1$ 辺の長さが等しい正方形の辺を貼り合わせて新たな長方形を作る.
この操作を続けるとき, 長方形の隣り合う $2$ 辺の長さの比はどのような値に近づいていくか. →答え
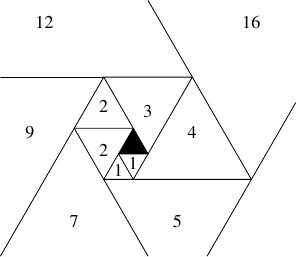
《らせん状に並べられた正三角形》図のように黒塗りの正三角形の周りに正三角形をらせん状に並べていくとき, 正三角形とその直前に並べられた正三角形の辺の長さの比はどのような値に近づいていくか.
極限値が存在することは証明なしに認めてよい. →答え
《くじで当たらない確率の極限値》$n$ 本中 $1$ 本だけ当たりが入ったくじを $n$ 回引くときに $1$ 回も当たらない確率は, $n$ が大きくなるにつれてどのような値に近づいていくか.
ただし, 引いたくじは毎回もとに戻すものとする. →答え
《硬貨を投げる回数の期待値》表が出る確率も裏が出る確率も $\dfrac{1}{2}$ である硬貨を表が出るまで投げ続けるとき, 何回目に投げ終わると見込まれるか. →答え
《労働者の報酬》
- (1)
- $1$ 日目に $1$ 人の労働者がおり, $n$ 日目 $(n \geqq 2)$ に $n$ 人の労働者が増える.
毎日 $a$ 円の報酬を労働者全員で均等割りするとして無限に働き続けるとき, $1$ 日目からいる労働者が得られる報酬は合わせて何円か.
- (2)
- $1$ 日目に $1$ 人の雇用人がおり, $n$ 日目 $(n \geqq 2)$ に $2n-1$ 人の労働者が増える.
毎日 $a$ 円の報酬を労働者全員で均等割りするとして無限に働き続けるとき, $2$ 日目からいる労働者が得られる報酬は合わせて何円か.
→答え
《元気な犬が走った道のり》主人が犬を連れて家に帰る途中, 家から $a$ m の地点に来たとき, 犬は先に家に向かって走り出し, 家に着くとすぐに引き返して主人の元へ戻ってきた.
すると, またすぐに家に向かって走り出し, 家に着くとすぐに引き返して主人の元へ戻る.
犬は, 主人が歩く速さの $r$ 倍の速さで, 主人が家に着くまで, このような往復運動を繰り返す.
犬が $n$ 回目に家に向かって走り出したときの家までの道のりは何 m か.
また, 主人が家に着くまでに犬は何 m 走るか. →答え
《ヴィエトの公式の幾何学的意味》斜辺の長さが $1$ の直角二等辺三角形を $1$ 個目の直角三角形として, 直角三角形の大きい方の鋭角の対辺と $1$ 辺を共有する直角三角形を作るという操作を, 小さい方の鋭角の大きさが毎回半減するように続けていく.
このとき, 新たに作られる直角三角形の斜辺の長さはどのような値に近づいていくか. →答え
《半円形の鏡による光の反射》円柱を縦に $2$ 等分した形の鏡張りの部屋の隅 $\mathrm A$ から曲面の壁に向かって水平に光を発射する.
その発射方向を部屋のもう一方の隅 $\mathrm B$ に近づけていくとき, 反射した光が平面の壁に当たる点 $\mathrm P$ と部屋の隅との距離の比 $\mathrm{AP}:\mathrm{BP}$ はどのような値に近づいていくか.
ただし, この部屋では, 曲面の壁と平面の壁が交差する部分を部屋の隅と呼ぶ. →答え
微分法
《ケプラーのワイン樽の問題》中に一定の長さの棒が入るように円柱形のワイン樽を作る.
容積を最大にするには, 底面の直径, 高さ, 棒の長さの比をどのような値にすればよいか.
ただし, 棒の太さは考えないものとする. →答え
《正方形の紙で作れる最大の箱》正方形の紙の四隅から正方形を取り除き, その残りを折り曲げて, ふたのない正四角柱の箱を作る.
容積を最大にするには, 底面の $1$ 辺の長さと高さの比をどのような値にすればよいか.
ただし, 紙の厚さは考えないものとする. →答え
《カプセルに入る最大の積み木》球形のカプセルの中にできるだけ体積が大きい三角柱の積み木を入れるとき, その体積はカプセルの容積の何倍になるか. →答え
《円錐形の容器の容積の最大化》円形の薄い紙を $2$ つの扇形に切り分け, 小さくない方の扇形の直線部分を貼り合わせて, ふたのない円錐形の容器を作る.
容器の容積が最大になるようにするには, 中心角の大きさをいくらにすればよいか. →答え
《円柱の表面積の最小化》与えられた体積をもつ円柱を作るとき, 表面積が最小になるようにするには, 底面の半径と高さの比をいくらにすればよいか. →答え
《廊下を通過できる棒の長さの最大値》幅 $x,$ $y$ の通路が直角につながった廊下を, 水平に保ったまま通過できる棒の長さの最大値はいくらか.
ただし, 通路は十分に長いとし, 棒の太さは無視して考えるものとする. →答え
《おうぎ形の等周問題》$1$ 本の細いひもがある.
このひもを使って面積が最大になるようにおうぎ形の領域を囲むとき, 半径と弧の長さの比は何対何になるか. →答え
《与えられた辺長をもつ最大の四角形》与えられた正の数 $a,$ $b,$ $c,$ $d$ を $4$ 辺の長さとする四角形のうち面積が最大であるのはどのような四角形か. →答え
《円に内接する周長最大の $n$ 角形》$n$ を $3$ 以上の整数とする.
与えられた円に内接する $n$ 角形のうち周の長さが最大であるのはどのような $n$ 角形か.
(ヒント: 次の $\sin x$ に関する「イェンセンの不等式」を利用する:
$n$ を $2$ 以上の整数とし, $t_1,$ $\cdots,$ $t_n > 0,$ $t_1+\cdots +t_n = 1$ とする.
$x_1,$ $\cdots,$ $x_n \in (0,\pi )$ のとき, $\displaystyle\sin\left(\sum_{k = 1}^nt_kx_k\right) \geqq \sum_{k = 1}^nt_k\sin x_k$ が成り立ち, 等号成立は $x_1 = \cdots = x_n$ の場合に限る.) →答え
《円に内接する面積最大の $n$ 角形》
- (A)
- 与えられた円に内接する三角形のうち面積が最大であるのはどのような三角形か.
- (B)
- 与えられた円に内接する $n$ 角形のうち面積が最大であるのはどのような $n$ 角形か.
→答え
《紙が重なった部分の面積の最小値》正方形の紙を $2$ 本の対角線の交点を通る直線で折り, 紙が重なった部分の面積が最小になるようにするとき, その面積が紙全体の面積に占める割合はいくらか. →答え
積分法
《棒の通過範囲の面積》鉛直な壁に垂直に立てかけられた細い棒が水平な床に, 上端が壁に接したまま下端が床をすべりながら倒れた.
このときの棒の通過範囲の面積は, 下端を中心に回転して倒れたときの何倍か. →答え
《円の周りを回転する円上の動点の軌跡》 円 $C$ は半径が同じ定円 $O$ の周りをすべることなく回転している.
$C$ 上の点 $\mathrm P$ が $O$ と接したときから再び $O$ と接するまで動くとき, $\mathrm P$ の軌跡が囲む領域の面積は $C$ の面積の何倍か. →答え
《ヤギの問題》平らな農場で, ヤギが円柱形の柱の一端に伸び縮みのしないひもでつながれている.
ひもの長さが柱の周の長さに等しいとき, ヤギが動き回れる範囲の面積は, 柱の断面積の何倍か.
ただし, ヤギの大きさ, ひもの太さとつなぎ目は考えないものとする. →答え
《パイプの共通部分の体積》前後, 左右, 上下方向に延びる内径の等しいパイプの軸が $1$ 点で直交するとき, $3$ 本のパイプの共通部分の体積は, パイプが円柱状である場合, 正四角柱である場合の何倍になるか. →答え
《タイヤの周上の点が動く長さ》タイヤの周上の $1$ 点はタイヤが $1$ 回転する間にタイヤの半径の何倍の長さを動くか. →答え
《棒の通過範囲の境界線の長さ》鉛直な壁に垂直に立てかけられた細い棒が水平な床に, 上端が壁に接したまま下端が床をすべりながら倒れた.
このときの棒の通過範囲の境界線の長さは, 棒の長さの何倍か. →答え
《円の伸開線の長さ》円に伸び縮みのしないひもをたるみなく巻きつけていくと, ちょうど $1$ 周したところで巻き終わった.
このとき, ひもの先端が描く曲線の長さはひもの長さの何倍か.
ただし, ひもの太さは無視して考えるものとする. →答え
《放物線の長さ》動点が放物線 $y = \dfrac{x^2}{4p}$ $(p \neq 0)$ 上の $0 \leqq x \leqq b$ の範囲を動くとき, どれだけの道のりを動くか. →答え
《バクテリアの増殖》あるバクテリアの増殖率はその時点の数に比例するという.
このバクテリアが $n$ 倍に増殖するまでにかかる時間と, $n$ 倍から $n^2$ 倍に増殖するまでにかかる時間はどちらが長いか. →答え
不等式
《$3$ 変数の相加・相乗平均の不等式》体積が $V$ である直方体の縦の長さ, 横の長さ, 高さの平均値と, 体積が $V$ である立方体の $1$ 辺の長さは, どちらの方が長いか. →答え
《積の和の最大値》$2$ 人 $1$ チームでゲームを行う.
全員が $1$ 番から $n$ 番までの合計 $n$ 枚の番号札を持ち, チームごとに $n$ 回に分けて $2$ 人同時に番号札を $1$ 枚ずつ場に出して, $2$ 枚の番号の積の合計をチームの得点とする.
このゲームの得点として考えられる値は最大でいくらか.
ただし, それぞれの番号札は $1$ 回しか使えないものとする. →答え
さまざまな解析学
《無理数の無理数乗》無理数の無理数乗として表される有理数は存在するか.
存在する場合にはその一例を挙げ, 存在しない場合にはその理由を説明せよ. →答え
《$2$ つの整数の整数乗が等しくなる条件》$a,$ $b$ を $1$ より大きい整数とする.
$a$ を整数乗した値と $b$ を整数乗した値が等しくなるのはどのような場合か. →答え
幾何学
初等幾何学
《トリチェリーの問題》$3$ つの工場 A, B, C からなる工業地域に $1$ つの変電所を建てる.
変電所からそれぞれの工場までの送電線の長さの和が最小になるようにするには, 変電所をどのような位置に建てればよいか.
ただし, $\triangle\mathrm{ABC}$ のすべての内角は $120^\circ$ 未満であるとする.
(ヒント: 平面ベクトル $\vec v\,(\neq \vec 0),$ $\vec w$ に対して $|\vec v-\vec w| \geqq |\vec v|-\dfrac{\vec v}{|\vec v|}\cdot\vec w$ が成り立つ.) →答え
《$3$ 点からの距離の平方和が最小の点》平面において, $\triangle\mathrm{ABC}$ の $3$ 頂点からの距離の $2$ 乗の和が最小である点はどのような点か. →答え
《ナポレオンの定理》平面おいて $\triangle\mathrm{ABC}$ の外側に正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかき, それらの重心をそれぞれ $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ とおく.
$\triangle\mathrm A''\mathrm B''\mathrm C''$ はどのような形の三角形か. →答え
《レギオモンタヌスの問題》フィールドの中央から $d$ だけ離れたセンターライン上の地点から, 選手が敵陣のゴールラインに向かって真っすぐ進んでいる.
ゴールの幅が $w$ であるとき, ゴールを見込む角が最大になるという意味でシュートを放つのに最も適しているのは, ゴールラインからどれだけ離れた地点か.
ただし, $d > \dfrac{w}{2}$ とする. →答え
《正多角形の辺と対角線の長さの総和》ペンキで正 $n$ 角形の周とそのすべての対角線を描くとき, 周のみを描くときの何倍のペンキを使うか. →答え
《正七角形調和》正七角形 $\mathrm{ABCDEFG}$ の形をした公園があり, 各頂点から他の頂点に向かって真っすぐな歩道が伸びている.
B さん, C さんがそれぞれ点 $\mathrm B,$ $\mathrm C$ から点 $\mathrm G$ に向かって真っすぐに歩いたところ, 所要時間は同じになった.
A さんが B さん, C さんの平均の速さで点 $\mathrm A$ から点 $\mathrm G$ に向かって真っすぐに歩くとき, 所要時間は B さんの何倍になるか. →答え
解析幾何学
《光の照射範囲》床の上の光源 $\mathrm O$ から, 天井から垂らされたスクリーン上の点 $\mathrm C$ に向かって光を照射したところ, 真横から見て, 光はスクリーンの下端 $\mathrm A$ から上端 $\mathrm B$ にまで達し, スクリーンの真下にある床の上の点を $\mathrm H$ として $\mathrm{OH} = \mathrm{HA} = \mathrm{AC}$ となった.
このとき, 点 $\mathrm B$ の床からの距離は点 $\mathrm A$ の床からの距離の何倍になるか. →答え
《等面四面体の体積》たかし君は, $3$ 辺の長さが $a,$ $b,$ $c$ である鋭角三角形の板 $4$ 枚を貼り合わせて正四面体のオブジェを作った.
このオブジェの体積はいくらか. →答え
《オイラーの不等式》円柱に $3$ 枚の薄い長方形の板を貼り付けて三角柱を作り, これを回転させることで新しい円柱を作る.
新しい円柱の半径が最小になるようにするとき, その半径はもとの円柱の半径の何倍になるか. →答え
《三角形の外接円と内接円の半径の比》$3$ 辺の長さと面積が整数である三角形は「ヘロンの三角形」と呼ばれ, その外接円, 内接円の半径が有理数であることはよく知られている.
それでは, $3$ 辺の長さが整数である三角形において外接円の半径に対する内接円の半径の比は有理数であるという主張は正しいか.
正しければ証明を与え, 誤りであれば反例を挙げよ. →答え
《球に入る最大の正多面体》球状のカプセルにできるだけ体積の大きい正多面体の模型を入れたい.
どの正多面体の模型を入れればよいか. →答え
《三角柱の側面の勾配》三角柱のブロックを横にして平らな床で転がすと, 側面が床につく度に斜面の勾配が整数になった.
このとき, 各勾配の値はいくらか. →答え
《傾きの関係式》ある街に $3$ つの坂があり, 最も緩い坂の斜度は他の $2$ つの坂の斜度の差に等しいという.
鉛直方向に $1$ m 上るために水平方向に進まなければならない距離が最もきつい坂で $x$ m, $2$ 番目にきつい坂で $(x+1)$ m であるとき, この距離は最も緩い坂で何 m になるか. →答え
《正接の和の最小値》大きな鋭角三角形のオブジェを作る.
三角形の各頂点から反時計周りに辺に沿って $1$ だけ進んだ点から進行方向に対して垂直な方向に辺にぶつかるまで支柱を伸ばす.
$3$ 本の支柱の長さの和を最小にするには, オブジェをどうような形にすればよいか. →答え
《楕円に内接する三角形》楕円に内接する三角形について, 楕円に占める三角形の面積の割合は最大でいくらになるか. →答え
《ヘロンの公式》$3$ 辺の長さが $a,$ $b,$ $c$ である三角形の面積 $S$ はどのように表されるか. →答え
《ブラーマグプタの公式とパラメシュヴァーラの公式》
- (1)
- 円に内接し, $4$ 辺の長さが $a,$ $b,$ $c,$ $d$ である四角形の $S$ は $a,$ $b,$ $c,$ $d$ を用いてどのように表されるか.
- (2)
- $4$ 辺の長さが $a,$ $b,$ $c,$ $d$ である四角形が円に内接するとき, その半径 $R$ は $a,$ $b,$ $c,$ $d$ を用いてどのように表されるか.
(ヒント: 円に内接する四角形 $\mathrm{ABCD}$ において $\mathrm{AC}\cdot\mathrm{BD} = \mathrm{AB}\cdot\mathrm{CD}+\mathrm{BC}\cdot\mathrm{DA}$ が成り立つという「トレミーの定理」を用いる.)
→答え
《三角形の等周問題》周の長さが一定の三角形のうち面積が最大のものはどのような形の三角形か. →答え
《座標法》頂点の座標が $(x_1,y_1),$ $\cdots,$ $(x_n,y_n)$ である $n$ 角形の面積 $S$ はどのように表されるか. →答え
《棒の継ぎ目の軌跡》長さが $a,$ $b$ $(a \neq b)$ の棒を $1$ 本につなぎ, 新たな棒を作る.
これを両端が L 字型の壁を伝うように動かすとき, 棒の継ぎ目はどのような軌跡を描くか. →答え
《引きずられた荷物の軌跡》伸び縮みのしない長さ $1$ のひもの先端に荷物がくくり付けられている.
荷主が $xy$ 平面上の原点 $\mathrm O$ から $x$ 軸正方向へ荷物を引きずりながら移動するとき, 点 $(0,1)$ にあった荷物が描く軌跡はどのような式で表されるか.
$x \geqq 0$ の範囲で, 荷物が点 $\mathrm P$ にあるとき荷主が点 $\mathrm M$ にいるとして, $x$ 軸正方向と $\mathrm{MP}$ のなす角 $\theta$ を用いて表せ.
(ヒント: 点 $\mathrm P(x,y)$ における曲線の接線の傾き $\dfrac{dy}{dx}$ は直線 $\mathrm{MP}$ の傾きに等しいこと, $x$ は $y = 1$ において連続であることを利用する.) →答え
離散幾何学
《正平面充填形》平面に $1$ 種類の正多角形を隙間も重なりもなく敷き詰める方法は, 全部で何通りあるか.
ただし, 使用する正多角形はすべて同じ大きさであり, $3$ 枚以上の正多角形は頂点のみを共有する方法のみを考えるものとする. →答え
《一筆書きが可能な正多面体》正多面体のうち, すべての辺が一筆書きでなぞれるものはどれか. →答え
《正方形の頂点を結ぶ最短経路》分岐点を新たに設けてもよいとするとき, 正方形の $4$ 個の頂点を結ぶ最短経路の長さは正方形の周の長さの何倍か. →答え
《円を用いたヴェン図の限界》ある全体集合に属する集合を円で表し (集合の要素を円の内部または周上の点, 補集合の要素を円の外部の点に対応させる), 集合の共通部分を円の重なり (面積は正) で表す.
このとき, どのような集合も $1$ つの平面上に表せるのは, 集合が何個以下のときか. →答え
《楕円の周による平面の分割》$n$ 個の楕円の周により平面が分割されてできる領域の個数の最大値はいくらか. →答え
《平面における格子点を頂点とする正三角形》方眼紙において, 横方向の罫線と縦方向の罫線の交点を格子点と呼ぶ.
$3$ 個の格子点を頂点とするような正三角形は存在するか.
存在するならばその一例を挙げ, 存在しないならばその理由を述べよ. →答え
《空間における格子点を頂点とする正六角形》平面や空間において, 座標の各成分が整数である点を格子点と呼ぶ.
平面において $6$ 個の格子点を頂点とするような正六角形は存在しないことが知られている.
それでは, 空間において $6$ 個の格子点を頂点とするような正六角形は存在するか.
存在するならばそのような正六角形の $1$ 辺の長さの最小値を求め, 存在しないならばその理由を述べよ. →答え
《シュタインハウスの問題》方眼紙において, 横方向の罫線と縦方向の罫線の交点を格子点と呼ぶ.
与えられた正の整数 $n$ に対して, ちょうど $n$ 個の格子点を含むような円は存在するか.
ヒント: 点 $\left(\sqrt 2,\dfrac{1}{3}\right)$ からそれぞれの格子点までの距離を考えてみよ. →答え
《頂点と内心が格子点である鋭角三角形》$xy$ 平面において $x$ 座標も $y$ 座標も整数である点を格子点と呼ぶ.
格子点を頂点とする鋭角三角形のうち, 内心も格子点である三角形の例を挙げよ. →答え
《三角格子上の正六角形の個数》正六角形 $H$ の各辺を $n$ 等分する点をとり, そのうち $H$ の辺と平行な直線上にある $2$ 点をそれぞれ線分で結ぶ (いわゆる「三角格子」を作る).
このとき, これらの線分, または $H$ の辺, 最長対角線 (まとめて「格子線」と呼ぶ) で囲まれた正六角形は何個あるか. →答え
さまざまな幾何学
《コッホ雪片の一般化》$p$ を $3$ 以上の整数とする.
$K_0$ を正 $p$ 角形として, 多角形 $K_n$ $(n \geqq 0)$ の各辺の $3$ 等分点を隣り合う $2$ つの頂点とするような正 $p$ 角形を $K_n$ の外側に重なりを許して貼り合わせることで多角形 $K_{n+1}$ を定める.
このとき, $K_n$ ののべ面積 (重なりも加算) が有限な値に近づいていく $p$ の最大値はいくらか. →答え
組合せ論・確率論
組合せ論
《試合数》総当たりのリーグ戦の試合数, トーナメント戦で優勝チームを決めるのに必要な試合数を比較するとき, 前者が後者を上回るのは, 参加チームが何チーム以上のときか. →答え
《パスワードの作り方》$2n$ 個の文字を各文字の候補として $n$ 文字のパスワードを作る.
重複する文字がある確率が重複する文字がない確率より高くなるのは, パスワードが何文字のときか. →答え
《正多面体の塗り分け》$p = 4,$ $6,$ $8,$ $12,$ $20$ とする.
$p$ 色を使って正 $p$ 面体の各面に互いに異なる色を塗る方法はそれぞれ何通りあるか. →答え
《$6$ 本の棒を辺とする四面体の総数》長さの異なる $6$ 本の棒があり, どの $3$ 本を選んでもそれらを辺とする三角形が作れるとする.
このとき, これらの棒を辺とする四面体は何通り作れるか.
ただし, $2$ つの四面体は, 平行移動や回転移動によって重なるとき同じ四面体とみなすが, 互いに鏡像の関係にあるとき異なる四面体とみなすものとする. →答え
《公平にものを分配する方法》異なる $nr$ 個のものを $n$ 人に $r$ 個ずつ配る方法は何通りあるか. →答え
《偶数個のものを選ぶ方法》異なる $n$ 個のものから偶数個 ($2$ 個以上) のものを選ぶ方法は全部で何通りあるか. →答え
《リーグ戦で全チームの勝敗の数が異なる確率》$n$ チームが参加する総当たりのリーグ戦において, 全チームの勝敗の数が異なる確率はいくらか.
ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする. →答え
《リーグ戦で全チームが引き分ける確率》$2n+1$ チーム $(n \geqq 1)$ が参加する総当たりのリーグ戦において, 全チームが $n$ 勝 $n$ 敗で引き分ける確率はいくらか.
ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする. →答え
《正多角形の頂点を結ぶ鋭角三角形》正 $n$ 角形 $(n \geqq 3)$ の頂点を結ぶ三角形のうち, 鋭角三角形が占める割合はいくらか. →答え
《完全順列の割合》$n$ 人 $(n \geqq 2)$ の席替えで全員の席が替わる確率 $p_n$ の最大値, 最小値はいくらか (高校生向け).
また, $n$ が大きくなるにつれて $p_n$ はどのような値に近づいていくか (大学生向け). →答え
《番勝負が最終戦までもつれ込む確率》A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行うとき, 対戦が最終戦までもつれ込む確率はいくらか.
ただし, A, B の実力は互角であり, 引き分けはないとする. →答え
《番勝負でリードを許さずに優勝する場合の数と確率》A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行う.
- (A)
- A が B に $1$ 度もリードを許さずに優勝する場合の数が素数になるのは何番勝負を行ったときか.
- (B)
- A が B に $1$ 度もリードを許さずに優勝する確率はいくらか.
ただし, A, B の実力は互角であり, 引き分けはないとする. →答え
《ベルトランの投票問題》選挙で A は $a$ 票を得て, B はそれより少ない $b$ 票を得た.
投票中にずっと A の得票数が B の得票数を上回っていた確率はいくらか.
ただし, どの順序で投票されることも同様に確からしいとする. →答え
《弦の交点の個数》円に互いに平行でない $n$ 本の弦を引くとき, 交点の個数は最大でいくらになるか. →答え
《ケーキ数》A, B の $2$ 人がそれぞれ $1$ ホールのケーキを切り分ける.
A は毎回ピースを一列に並べ直してから切り, B はケーキを固定したまま切る.
できるだけ多くのピースに切り分けるとき, ピースの個数で A が B を上回るのは, 何回ナイフを入れたときか.
ただし, ナイフは空間内のどの方向にでも真っすぐに入れられるものとし, $1$ 回の入刀で切断面が通るピースをすべて切り分けるものとする. →答え
確率論
《ド・メレの $2$ つのさいころ》$1$ つのさいころを $4$ 回ふって $6$ の目が出れば勝ちというゲーム A と, $2$ つのさいころを $24$ 回ふって $6$ のぞろ目が出れば勝ちというゲーム B は, どちらの方が勝つ確率が高いか. →答え
《賞金の分配問題》$2$ 人で公平な勝負を繰り返し, 先に $3$ 回勝った方が賞金をすべてもらうというゲームを A が $2$ 勝, B が $1$ 勝の段階で中止するとき, 賞金はどのような割合で A, B に分配するべきか. →答え
《コイン投げの確率の最大値》表, 裏が等確率で出る $1$ 枚のコインがある.
これをちょうど $r$ 回表が出る確率が最大となるような回数だけ投げるとき, 何回投げればよいか. →答え
《モンティ・ホール問題》$3$ つのドア A, B, C のうち, いずれかのドアの向こうに賞品が無作為に隠されている.
挑戦者はドアを $1$ つだけ開けて, 賞品があれば, それをもらうことができる.
挑戦者がドアを選んでからドアを開けるまでの間に, 司会者は残った $2$ つのドアのうち, はずれのドアを $1$ つ無作為に開ける.
このとき, 挑戦者は開けるドアを変更することができる.
ドアを変更するとき, しないときのどちらが賞品を得る確率が高いか. →答え
《ホイヘンスの第 $2$ 問題》袋の中に赤玉が $a$ 個, 白玉が $b$ 個入っている.
あるクラスの生徒 $n$ 人が玉を $1$ 個取り出して戻すという操作を誰かが赤玉を取り出すまで出席番号順に何巡でも繰り返すとき, $k$ 番の生徒が赤玉を取り出す確率はいくらか. →答え
《$n$ 回以下のじゃんけんで順位が決まる確率》$3$ 人がじゃんけんをして, $n$ 回以下で $1$ 位から $3$ 位までの順位が決まる確率はいくらか.
ただし, $3$ 人の手の出し方は, どれも同様に確からしいとする. →答え
《誕生日が一致する確率》公転周期が $n$ 日の惑星で集会を開く.
同じ誕生日の人がいる確率が $2$ 分の $1$ 以上になるのは, この惑星の住人が何人以上集まったときか.
$x$ が十分に小さいとき近似式 $1-x \fallingdotseq e^{-x}$ ($e$: ネイピア数), $a^{x(x-1)} \fallingdotseq a^{x^2}$ $(0 < a < 1)$ が成り立つことを利用して解け. →答え
《ポリアの壺》最初, 壺の中に色 $1$ の玉が $a_1$ 個, $\cdots,$ 色 $r$ の玉が $a_r$ 個だけ入っている.
壺の中から無作為に玉を $1$ 個取り出して, その玉と同じ色の玉を $c$ 個だけ壺の中に入れ, 取り出した玉も戻すという試行を繰り返す.
$n$ 回目に色 $i$ $(1 \leqq i \leqq r)$ の玉を取り出す確率はいくらか. →答え
《破産の確率》A は $m$ 個, B は $n$ 個のあめを持っている.
$2$ 人はゲームを行い, 勝者が敗者から $1$ 個のあめをもらうという試行を, 一方のあめがなくなるまで繰り返す.
各回のゲームで A の勝率が $a,$ B の勝率が $b$ $(0 < a \leqq b < 1)$ であり, 引き分けはないとするとき, B のあめがなくなる確率はいくらか. →答え
《くじ引きのサドンデス》つぼの中に赤玉, 白玉を入れ, $2$ 人が交互に玉を $1$ 個ずつ取り出して, 先に赤玉を取り出した者を勝者とするゲームを行う.
どのように赤玉, 白玉を入れれば先手, 後手の勝率が等しくなるか.
ただし, 取り出した玉は, もとに戻さないものとする. →答え
《巴戦で優勝する確率》A, B, C の $3$ 選手が巴戦で優勝決定戦を行う.
A, B の対戦から始めて, $2$ 試合目以降は直前の試合の勝者と控えの選手が対戦し, 先に $2$ 連勝した選手を優勝とする.
$3$ 選手の実力が互角であり, 各試合で引き分けはないとするとき, A, B, C が優勝する確率の比は何対何対何か. →答え
《三角形の周上のランダム・ウォーク》正三角形 $\mathrm{ABC}$ の頂点 $\mathrm A$ にいるアリが $1$ 秒ごとに異なる頂点に等確率で移動していくとき, $n$ 秒後に頂点 $\mathrm A$ にいる確率はいくらか. →答え
《紅白まんじゅうの交換》A, B がそれぞれ紅白のまんじゅうが $1$ 個ずつ入った袋を持っている.
A, B が各自の袋からまんじゅうを $1$ 個取り出して交換して袋にしまうという操作を $n$ 回繰り返したとき, A, B がともに紅白のまんじゅうを $1$ 個ずつ持っている確率はいくらか. →答え
《テニスの勝率》A, B がテニスの試合している.
A のサービス・ゲームにおいて, A のポイント獲得率が B のポイント獲得率の $2$ 倍であるとき, デュースになった時点から A がこのゲームをとる確率はいくらか. →答え
《ポリアの壺における期待値》最初に色 $1$ の玉が $a_1$ 個, $\cdots,$ 色 $r$ の玉が $a_r$ 個だけ入っていた壺の中から無作為に玉を $1$ 個取り出して, その玉と同じ色の玉を $c$ 個だけ壺の中に入れ, 取り出した玉も戻すという試行を繰り返すとき, $n$ 回目の試行後に壺に入っている色 $i$ の玉の個数の期待値はいくらか. →答え
《じゃんけんの勝者の人数》$1$ 回だけじゃんけんをするとき, 勝者の人数が最も多くなると見込まれるのは, 何人でじゃんけんをするときか. →答え
《赤玉が出るまでに取り出す玉の個数》$r$ 個の赤玉を含む $n$ 個の玉を袋に入れる.
- (1)
- 赤玉が出るまで $1$ 個ずつ玉を取り出すとき, 何個目に赤玉を取り出すと見込まれるか.
- (2)
- すべての赤玉が出るまで $1$ 個ずつ玉を取り出すとき, 何個目に最後の赤玉を取り出すと見込まれるか.
ただし, 取り出した玉は元に戻さないものとする. →答え
《仕切り板の間にある本の冊数》$n$ 冊の本と $r$ 枚の仕切り板がある.
これらを無作為に $1$ 列に並べて空の本棚に収納するとき, 隣り合う $2$ 枚の仕切り板の間にある本は平均的に何冊になると見込まれるか. →答え
《夫婦円卓問題》$n$ 組 $(n \geqq 2)$ の夫婦 $2n$ 人が, 男女交互に, それ以外は無作為に円卓の周りに座るとき, 隣どうしに座ると見込まれる夫婦は何組か. →答え
《さいころですべての目を出すまでにかかる回数》$n$ 面のさいころがある.
すべての目を出すには, 平均的に何回さいころをふればよいと見込まれるか (ヒント: 正の整数全体を値域とする確率変数 $W$ の期待値は $E(W) = \displaystyle\sum_{m = 1}^\infty m\,P(W = m)$ で定義される). →答え
《完全数》$p,$ $q$ を素数とする. $p\times q$ マスの余白のない方眼紙を罫線に沿って $1$ 個以上の合同な小長方形に分ける. このような分け方すべてにわたる小長方形の個数の総和がマス目の個数の $2$ 倍に等しいとき, $pq$ の値はいくらか. →答え
《カルキン=ウィルフ木》$\dfrac{1}{1}$ から始めて, 既存の各分数に対して, ①分子はそのままで, もとの分母ともとの分子の和を分母として, 新たな分数を作る, ②分母はそのままで, もとの分母ともとの分子の和を分子として, 新たな分数を作る, という $2$ つの操作を延々と繰り返す. このとき, 作られる分数の中に現れない正の有理数は存在するか. 存在する場合にはその例を挙げ, 存在しない場合にはそのことを証明せよ. →答え
《有理数の単位分数の和への分解》$0$ より大きく $1$ より小さいすべての有理数は, 有限個の相異なる正の整数の逆数の和として表すことができるか. 可能な場合には証明を述べ, 不可能な場合には反例を挙げよ. (ヒント: 分母を分子で割った商が $q$ であるとき, $q+1$ の逆数を $1$ つの項として考えてみよ.) →答え
《フロベニウスの硬貨交換問題》$a,$ $b$ を互いに素な $1$ より大きい整数とする. $a$ 円硬貨, $b$ 円硬貨のみを使ってちょうど支払えない金額は最大で何円か. ただし, 各硬貨は何枚使ってもよいが, おつりはもらえないものとする. →答え
《底面積と側面積が等しい整数三角柱》高さが $1$ であり, 残りの辺の長さも整数であって, 底面積と側面積が等しい三角柱は何個あるか. →答え
《底面積と側面積が等しい整数直方体》高さが整数 $z$ であり, 残りの辺の長さも整数であって, 底面積と側面積が等しい直方体は何個あるか. →答え
《ピタゴラスの $3$ つ組に現れる整数》同じ長さのマッチ棒をつなげて直角三角形の枠を作るとき, $1$ 辺に使われるマッチ棒の本数として考えられない整数の最大値はいくらか. →答え
《辺長が整数である格子三角形の面積》方眼紙の罫線 (間隔は $1$) の交点を頂点とする三角形において, 各辺の長さが整数であるならば面積も整数である, という主張は正しいか. 正しければ証明し, 正しくなければ反例を挙げよ. →答え
《平方三角数》正方形 (中実方陣) の形に並べられた複数個の石を, $1$ 段目に $1$ 個, $\cdots,$ $k$ 段目に $k$ 個, $\cdots$ と並べ直していくと, 正三角形の形に余すことなく並べられた. このとき, 考えられる石の個数として最も少ない個数は何個か. →答え
《出席番号の和》複数人の生徒からなるクラスの全員が出席番号順に $1$ 列に並んでいる. 列の先頭と最後尾からそれぞれ生徒の出席番号の和をとっていったとき, 出席番号が奇数である生徒で $2$ つの和が等しくなった. この生徒の出席番号として考えられる値は最小でいくらか. →答え
《辺長が等差数列をなすヘロンの三角形》$1$ 辺の長さが $1$ のマッチ棒をつなげて, 鋭角三角形の枠を作る. 各辺で使う本数が等差数列になり, 面積が整数になるようにするとき, 考えられるマッチ棒の本数として最も少ない本数は何本か. →答え
《有理点の距離》$xy$ 平面において $x$ 座標も $y$ 座標も有理数である点を有理点と呼ぶ. $2$ つの有理点の間の距離が $1,$ $\sqrt 2$ となることはある. それでは, $2$ つの有理点の間の距離が $\sqrt 3$ となることはあるか. →答え
《平方四角錐数》正方形 (中実方陣) の形に並べられた複数個の球を, $1$ 段目に $1$ 個, $\cdots,$ $k$ 段目に $k$ 個, $\cdots$ となるように積み上げていくと, 正四角錐の形に余すことなく並べられた. このとき, 考えられる球の個数として最も少ない個数は何個か. →答え
《ハーディー=ラマヌジャンのタクシー数》ラマヌジャンは療養中, ハーディー教授が見舞いに訪れた際に, “乗ってきたタクシーの番号は $1729$ だった. さして特徴のない数字だったよ”という教授に対して, すぐさま “そんなことはありません, とても興味深い数字です. それは $2$ つの立方数の和として $2$ 通りに表せる最小の数です” と答えたという. $1729$ は立方数の和としてどのように表されるか. $2$ 通りの表し方を答えよ. →答え
《累乗の差》バレーボール, キンボール ($3$ チームが $1$ つのコートに入って戦う球技) のトーナメント大会がそれぞれ開かれた. $2$ つの大会の出場チーム数の差は $1$ であり, 各大会でどのチームも $1$ 回戦を戦ったという. このとき, 各大会の出場チーム数はいくらか. →答え
《累乗の和》三角柱, 四角柱, 五角柱の鉛筆があり, それらの側面には互いに異なる文字が $1$ 個ずつ彫られている. A さんは三角柱, 四角柱の鉛筆のどちらかをランダムに選び, 三角柱の鉛筆であればそれを $x$ 回, 四角柱の鉛筆であればそれを $y$ 回転がす. B さんは五角柱の鉛筆を $z$ 回転がす. A さん, B さんの文字の出方の総数が一致するとき, $x,$ $y,$ $z$ の値はいくらか. →答え
《条件付きフェルマー方程式》$n$ を正の整数とする. $z \leqq n$ のとき, $x^n+y^n = z^n$ は正の整数解をもつか. →答え
《$3$ 種類のケーキ》同じ大きさの $3$ 種類のホール型のケーキを, $1$ 切れの大きさが種類によって異なるように, それぞれ何等分かに切り分ける. 種類ごとに $1$ 切れずつ集めたときの合計の大きさが, $1$ ホール分未満で, できるだけ大きくなるようにするには, 各ケーキを何等分に切り分ければよいか. →答え
《$1$ 階と $2$ 階の部屋割り》$1$ 階の $m$ 個の部屋には $n$ 人を泊め, $2$ 階の $n$ 個の部屋には $m$ 人を泊めた. 各階で考えられる部屋割りの総数は互いに等しく, 各階の宿泊者数は互いに異なるという. このとき, 何人の宿泊者がいたか. →答え
《フォンタナの三角形》番号札を A, B に配る. 番号の小さい方から A に $2$ 枚, B に $1$ 枚, $\cdots,$ A に $n+1$ 枚, B に $n$ 枚, $\cdots$ と配っていくとき, $n$ 回目に A に配られる札の番号の和 $S_n$ と B に配られる札の番号の和 $T_n$ の間にはどのような関係があるか. →答え
《カードの番号の積の総和の最大値》A, B がそれぞれ $1$ 番から $n$ 番までの番号札を持っている. A, B が手札から $1$ 枚ずつ同時に番号札を切っていくとき, 各回の番号の積の総和は最大でいくらになるか. →答え
《ハノイの塔》地面に $3$ 本の棒 A, B, C が立てられており, 棒 A に穴の開いた半径の異なる $n$ 枚の円盤が半径の大きい順に通されている.
- (1)
- すべての円盤を棒 B に移す手数の最小値はいくらか.
- (2)
- 円盤に半径の大きい方から $2$ 枚ごとに白色, 黒色の順に色が塗られているとする. 白色の円盤を棒 B, 黒色の円盤を棒 C に移す手数の最小値はいくらか.
- (2)'
- (2) の最後の状態から棒 B と棒 C の円盤を入れ替える手数の最小値はいくらか.
- (3)
- 円盤に半径の大きい方から $3$ 枚ごとに白色, 灰色, 黒色の順に色が塗られているとする. 白色の円盤を棒 A, 灰色の円盤を棒 B, 黒色の円盤を棒 C に移す手数の最小値はいくらか.
《うなぎの寝床での畳の敷き方》ちょうど $n$ 枚の畳が敷けるような長方形のうなぎの寝床に畳を敷く方法は何通りあるか. ただし, 寝床の縦の長さは畳の長い方の辺の長さに等しく, 横の長さは畳の短い方の辺の長さの $n$ 倍に等しいとする. →答え
《$1$ 段飛ばしを許した階段の登り方》$1$ 歩目は $1$ 段だけ上るとし, $2$ 歩目以降は $1$ 歩で $1$ 段上ることも $2$ 段上ることもできるとするとき, $n$ 段以下の階段を上る方法は全部で何通りあるか. →答え
《フィボナッチ数列の周期性》$F_1 = F_2 = 1,$ $F_{n+2} = F_n+F_{n+1}$ で定まる数列 $\{ F_n\}$ は「フィボナッチ数列」として広く知られている. どのような $n$ に対して $F_n$ は偶数になるか. →答え
《円卓における席替え》それぞれが動かないか隣に移るように円卓の周りに座った $n$ 人 $(n \geqq 3)$ を並べ替える方法は何通りあるか. →答え
《正四面体の辺上のランダム・ウォーク》正四面体 $\mathrm{ABCD}$ の頂点 $\mathrm A$ にいるアリが $1$ 秒ごとに異なる頂点に等確率で移動していくとき, $n$ 秒後に頂点 $\mathrm A$ にいる確率はいくらか. →答え
《$1$ 人飛ばしの継子立て》出席番号が $1$ 番から $n$ 番までの $n$ 人の生徒が順に $1$ つの輪を作るように並んでいる. 出席番号が $2$ 番の生徒から $1$ 人飛ばしで $1$ 人ずつ輪から抜けていくとき, 最後に残った生徒の出席番号はいくらか. ただし, $1$ 人飛ばしというルールは, 各時点で残っている生徒に対して考えるものとする. →答え
《カラビの三角形》$\angle\mathrm A$ が鈍角である二等辺三角形 $\mathrm{ABC}$ と, 互いに合同な $2$ つの正方形 $\mathrm{PQRS},$ $\mathrm{ATUV}$ があり, 頂点 $\mathrm P,$ $\mathrm T$ は辺 $\mathrm{AB}$ 上に, 辺 $\mathrm{QR}$ と頂点 $\mathrm U$ は辺 $\mathrm{BC}$ 上に, 頂点 $\mathrm S$ は辺 $\mathrm{AC}$ 上にあるとする. $\triangle\mathrm{ABC}$ の等辺に対する底辺の長さの比はある $3$ 次方程式を満たす. その $3$ 次方程式を求めよ. →答え
《奇数次方程式の実数解の存在》実数係数の奇数次の方程式 $f(x) = 0$ は少なくとも $1$ つの実数解をもつ, という主張は正しいか. 正しければ証明し, 正しくなければ反例を挙げよ. →答え
《合比の理》昨年, A 部と B 部の人数比は C 部と D 部の人数比と同じであった. 今年は, A 部に昨年の B 部と同じ人数が増え, B 部の人数は変わらず, C 部に昨年の D 部と同じ人数が増え, D 部の人数は変わらなかった. このとき, 今年の A 部と B 部の人数比, C 部と D 部の人数比についてどのようなことが言えるか. →答え
《$3$ 数の比》A, B, C の $3$ 人が $1$ 回ずつ輪投げをして, 全員無得点ではなく, A の得点は B の $p$ 倍, B の得点は C の $q$ 倍, C の得点は A の $r$ 倍になった. このとき, A, B, C の得点の比は何対何対何になるか. →答え
極限
《方眼の中の正方形》$n\times n$ マスの方眼の罫線に沿って描かれた正方形がマス目全体に占める面積の割合として見込まれる値は, $n$ が大きくなるにつれてどのような値に近づいていくか. →答え
《方眼の中の長方形》$n\times n$ マスの方眼の罫線に沿って描かれた長方形がマス目全体に占める面積の割合として見込まれる値は, $n$ が大きくなるにつれてどのような値に近づいていくか. →答え
《長方形の辺長の比の極限値》正方形の $1$ 辺に, それと $1$ 辺の長さが等しい正方形の辺を貼り合わせて長方形を作る. その長い方の辺に, それと $1$ 辺の長さが等しい正方形の辺を貼り合わせて新たな長方形を作る. この操作を続けるとき, 長方形の隣り合う $2$ 辺の長さの比はどのような値に近づいていくか. →答え
《らせん状に並べられた正三角形》図のように黒塗りの正三角形の周りに正三角形をらせん状に並べていくとき, 正三角形とその直前に並べられた正三角形の辺の長さの比はどのような値に近づいていくか. 極限値が存在することは証明なしに認めてよい. →答え
《くじで当たらない確率の極限値》$n$ 本中 $1$ 本だけ当たりが入ったくじを $n$ 回引くときに $1$ 回も当たらない確率は, $n$ が大きくなるにつれてどのような値に近づいていくか. ただし, 引いたくじは毎回もとに戻すものとする. →答え
《硬貨を投げる回数の期待値》表が出る確率も裏が出る確率も $\dfrac{1}{2}$ である硬貨を表が出るまで投げ続けるとき, 何回目に投げ終わると見込まれるか. →答え
《労働者の報酬》
《元気な犬が走った道のり》主人が犬を連れて家に帰る途中, 家から $a$ m の地点に来たとき, 犬は先に家に向かって走り出し, 家に着くとすぐに引き返して主人の元へ戻ってきた. すると, またすぐに家に向かって走り出し, 家に着くとすぐに引き返して主人の元へ戻る. 犬は, 主人が歩く速さの $r$ 倍の速さで, 主人が家に着くまで, このような往復運動を繰り返す. 犬が $n$ 回目に家に向かって走り出したときの家までの道のりは何 m か. また, 主人が家に着くまでに犬は何 m 走るか. →答え
《ヴィエトの公式の幾何学的意味》斜辺の長さが $1$ の直角二等辺三角形を $1$ 個目の直角三角形として, 直角三角形の大きい方の鋭角の対辺と $1$ 辺を共有する直角三角形を作るという操作を, 小さい方の鋭角の大きさが毎回半減するように続けていく. このとき, 新たに作られる直角三角形の斜辺の長さはどのような値に近づいていくか. →答え
《半円形の鏡による光の反射》円柱を縦に $2$ 等分した形の鏡張りの部屋の隅 $\mathrm A$ から曲面の壁に向かって水平に光を発射する. その発射方向を部屋のもう一方の隅 $\mathrm B$ に近づけていくとき, 反射した光が平面の壁に当たる点 $\mathrm P$ と部屋の隅との距離の比 $\mathrm{AP}:\mathrm{BP}$ はどのような値に近づいていくか. ただし, この部屋では, 曲面の壁と平面の壁が交差する部分を部屋の隅と呼ぶ. →答え
《方眼の中の長方形》$n\times n$ マスの方眼の罫線に沿って描かれた長方形がマス目全体に占める面積の割合として見込まれる値は, $n$ が大きくなるにつれてどのような値に近づいていくか. →答え
《長方形の辺長の比の極限値》正方形の $1$ 辺に, それと $1$ 辺の長さが等しい正方形の辺を貼り合わせて長方形を作る. その長い方の辺に, それと $1$ 辺の長さが等しい正方形の辺を貼り合わせて新たな長方形を作る. この操作を続けるとき, 長方形の隣り合う $2$ 辺の長さの比はどのような値に近づいていくか. →答え
《らせん状に並べられた正三角形》図のように黒塗りの正三角形の周りに正三角形をらせん状に並べていくとき, 正三角形とその直前に並べられた正三角形の辺の長さの比はどのような値に近づいていくか. 極限値が存在することは証明なしに認めてよい. →答え

《くじで当たらない確率の極限値》$n$ 本中 $1$ 本だけ当たりが入ったくじを $n$ 回引くときに $1$ 回も当たらない確率は, $n$ が大きくなるにつれてどのような値に近づいていくか. ただし, 引いたくじは毎回もとに戻すものとする. →答え
《硬貨を投げる回数の期待値》表が出る確率も裏が出る確率も $\dfrac{1}{2}$ である硬貨を表が出るまで投げ続けるとき, 何回目に投げ終わると見込まれるか. →答え
《労働者の報酬》
- (1)
- $1$ 日目に $1$ 人の労働者がおり, $n$ 日目 $(n \geqq 2)$ に $n$ 人の労働者が増える. 毎日 $a$ 円の報酬を労働者全員で均等割りするとして無限に働き続けるとき, $1$ 日目からいる労働者が得られる報酬は合わせて何円か.
- (2)
- $1$ 日目に $1$ 人の雇用人がおり, $n$ 日目 $(n \geqq 2)$ に $2n-1$ 人の労働者が増える. 毎日 $a$ 円の報酬を労働者全員で均等割りするとして無限に働き続けるとき, $2$ 日目からいる労働者が得られる報酬は合わせて何円か.
《元気な犬が走った道のり》主人が犬を連れて家に帰る途中, 家から $a$ m の地点に来たとき, 犬は先に家に向かって走り出し, 家に着くとすぐに引き返して主人の元へ戻ってきた. すると, またすぐに家に向かって走り出し, 家に着くとすぐに引き返して主人の元へ戻る. 犬は, 主人が歩く速さの $r$ 倍の速さで, 主人が家に着くまで, このような往復運動を繰り返す. 犬が $n$ 回目に家に向かって走り出したときの家までの道のりは何 m か. また, 主人が家に着くまでに犬は何 m 走るか. →答え
《ヴィエトの公式の幾何学的意味》斜辺の長さが $1$ の直角二等辺三角形を $1$ 個目の直角三角形として, 直角三角形の大きい方の鋭角の対辺と $1$ 辺を共有する直角三角形を作るという操作を, 小さい方の鋭角の大きさが毎回半減するように続けていく. このとき, 新たに作られる直角三角形の斜辺の長さはどのような値に近づいていくか. →答え
《半円形の鏡による光の反射》円柱を縦に $2$ 等分した形の鏡張りの部屋の隅 $\mathrm A$ から曲面の壁に向かって水平に光を発射する. その発射方向を部屋のもう一方の隅 $\mathrm B$ に近づけていくとき, 反射した光が平面の壁に当たる点 $\mathrm P$ と部屋の隅との距離の比 $\mathrm{AP}:\mathrm{BP}$ はどのような値に近づいていくか. ただし, この部屋では, 曲面の壁と平面の壁が交差する部分を部屋の隅と呼ぶ. →答え
微分法
《ケプラーのワイン樽の問題》中に一定の長さの棒が入るように円柱形のワイン樽を作る.
容積を最大にするには, 底面の直径, 高さ, 棒の長さの比をどのような値にすればよいか.
ただし, 棒の太さは考えないものとする. →答え
《正方形の紙で作れる最大の箱》正方形の紙の四隅から正方形を取り除き, その残りを折り曲げて, ふたのない正四角柱の箱を作る. 容積を最大にするには, 底面の $1$ 辺の長さと高さの比をどのような値にすればよいか. ただし, 紙の厚さは考えないものとする. →答え
《カプセルに入る最大の積み木》球形のカプセルの中にできるだけ体積が大きい三角柱の積み木を入れるとき, その体積はカプセルの容積の何倍になるか. →答え
《円錐形の容器の容積の最大化》円形の薄い紙を $2$ つの扇形に切り分け, 小さくない方の扇形の直線部分を貼り合わせて, ふたのない円錐形の容器を作る. 容器の容積が最大になるようにするには, 中心角の大きさをいくらにすればよいか. →答え
《円柱の表面積の最小化》与えられた体積をもつ円柱を作るとき, 表面積が最小になるようにするには, 底面の半径と高さの比をいくらにすればよいか. →答え
《廊下を通過できる棒の長さの最大値》幅 $x,$ $y$ の通路が直角につながった廊下を, 水平に保ったまま通過できる棒の長さの最大値はいくらか. ただし, 通路は十分に長いとし, 棒の太さは無視して考えるものとする. →答え
《おうぎ形の等周問題》$1$ 本の細いひもがある. このひもを使って面積が最大になるようにおうぎ形の領域を囲むとき, 半径と弧の長さの比は何対何になるか. →答え
《与えられた辺長をもつ最大の四角形》与えられた正の数 $a,$ $b,$ $c,$ $d$ を $4$ 辺の長さとする四角形のうち面積が最大であるのはどのような四角形か. →答え
《円に内接する周長最大の $n$ 角形》$n$ を $3$ 以上の整数とする. 与えられた円に内接する $n$ 角形のうち周の長さが最大であるのはどのような $n$ 角形か. (ヒント: 次の $\sin x$ に関する「イェンセンの不等式」を利用する: $n$ を $2$ 以上の整数とし, $t_1,$ $\cdots,$ $t_n > 0,$ $t_1+\cdots +t_n = 1$ とする. $x_1,$ $\cdots,$ $x_n \in (0,\pi )$ のとき, $\displaystyle\sin\left(\sum_{k = 1}^nt_kx_k\right) \geqq \sum_{k = 1}^nt_k\sin x_k$ が成り立ち, 等号成立は $x_1 = \cdots = x_n$ の場合に限る.) →答え
《円に内接する面積最大の $n$ 角形》
《紙が重なった部分の面積の最小値》正方形の紙を $2$ 本の対角線の交点を通る直線で折り, 紙が重なった部分の面積が最小になるようにするとき, その面積が紙全体の面積に占める割合はいくらか. →答え
《正方形の紙で作れる最大の箱》正方形の紙の四隅から正方形を取り除き, その残りを折り曲げて, ふたのない正四角柱の箱を作る. 容積を最大にするには, 底面の $1$ 辺の長さと高さの比をどのような値にすればよいか. ただし, 紙の厚さは考えないものとする. →答え
《カプセルに入る最大の積み木》球形のカプセルの中にできるだけ体積が大きい三角柱の積み木を入れるとき, その体積はカプセルの容積の何倍になるか. →答え
《円錐形の容器の容積の最大化》円形の薄い紙を $2$ つの扇形に切り分け, 小さくない方の扇形の直線部分を貼り合わせて, ふたのない円錐形の容器を作る. 容器の容積が最大になるようにするには, 中心角の大きさをいくらにすればよいか. →答え
《円柱の表面積の最小化》与えられた体積をもつ円柱を作るとき, 表面積が最小になるようにするには, 底面の半径と高さの比をいくらにすればよいか. →答え
《廊下を通過できる棒の長さの最大値》幅 $x,$ $y$ の通路が直角につながった廊下を, 水平に保ったまま通過できる棒の長さの最大値はいくらか. ただし, 通路は十分に長いとし, 棒の太さは無視して考えるものとする. →答え
《おうぎ形の等周問題》$1$ 本の細いひもがある. このひもを使って面積が最大になるようにおうぎ形の領域を囲むとき, 半径と弧の長さの比は何対何になるか. →答え
《与えられた辺長をもつ最大の四角形》与えられた正の数 $a,$ $b,$ $c,$ $d$ を $4$ 辺の長さとする四角形のうち面積が最大であるのはどのような四角形か. →答え
《円に内接する周長最大の $n$ 角形》$n$ を $3$ 以上の整数とする. 与えられた円に内接する $n$ 角形のうち周の長さが最大であるのはどのような $n$ 角形か. (ヒント: 次の $\sin x$ に関する「イェンセンの不等式」を利用する: $n$ を $2$ 以上の整数とし, $t_1,$ $\cdots,$ $t_n > 0,$ $t_1+\cdots +t_n = 1$ とする. $x_1,$ $\cdots,$ $x_n \in (0,\pi )$ のとき, $\displaystyle\sin\left(\sum_{k = 1}^nt_kx_k\right) \geqq \sum_{k = 1}^nt_k\sin x_k$ が成り立ち, 等号成立は $x_1 = \cdots = x_n$ の場合に限る.) →答え
《円に内接する面積最大の $n$ 角形》
- (A)
- 与えられた円に内接する三角形のうち面積が最大であるのはどのような三角形か.
- (B)
- 与えられた円に内接する $n$ 角形のうち面積が最大であるのはどのような $n$ 角形か.
《紙が重なった部分の面積の最小値》正方形の紙を $2$ 本の対角線の交点を通る直線で折り, 紙が重なった部分の面積が最小になるようにするとき, その面積が紙全体の面積に占める割合はいくらか. →答え
積分法
《棒の通過範囲の面積》鉛直な壁に垂直に立てかけられた細い棒が水平な床に, 上端が壁に接したまま下端が床をすべりながら倒れた.
このときの棒の通過範囲の面積は, 下端を中心に回転して倒れたときの何倍か. →答え
《円の周りを回転する円上の動点の軌跡》 円 $C$ は半径が同じ定円 $O$ の周りをすべることなく回転している. $C$ 上の点 $\mathrm P$ が $O$ と接したときから再び $O$ と接するまで動くとき, $\mathrm P$ の軌跡が囲む領域の面積は $C$ の面積の何倍か. →答え
《ヤギの問題》平らな農場で, ヤギが円柱形の柱の一端に伸び縮みのしないひもでつながれている. ひもの長さが柱の周の長さに等しいとき, ヤギが動き回れる範囲の面積は, 柱の断面積の何倍か. ただし, ヤギの大きさ, ひもの太さとつなぎ目は考えないものとする. →答え
《パイプの共通部分の体積》前後, 左右, 上下方向に延びる内径の等しいパイプの軸が $1$ 点で直交するとき, $3$ 本のパイプの共通部分の体積は, パイプが円柱状である場合, 正四角柱である場合の何倍になるか. →答え
《タイヤの周上の点が動く長さ》タイヤの周上の $1$ 点はタイヤが $1$ 回転する間にタイヤの半径の何倍の長さを動くか. →答え
《棒の通過範囲の境界線の長さ》鉛直な壁に垂直に立てかけられた細い棒が水平な床に, 上端が壁に接したまま下端が床をすべりながら倒れた. このときの棒の通過範囲の境界線の長さは, 棒の長さの何倍か. →答え
《円の伸開線の長さ》円に伸び縮みのしないひもをたるみなく巻きつけていくと, ちょうど $1$ 周したところで巻き終わった. このとき, ひもの先端が描く曲線の長さはひもの長さの何倍か. ただし, ひもの太さは無視して考えるものとする. →答え
《放物線の長さ》動点が放物線 $y = \dfrac{x^2}{4p}$ $(p \neq 0)$ 上の $0 \leqq x \leqq b$ の範囲を動くとき, どれだけの道のりを動くか. →答え
《バクテリアの増殖》あるバクテリアの増殖率はその時点の数に比例するという. このバクテリアが $n$ 倍に増殖するまでにかかる時間と, $n$ 倍から $n^2$ 倍に増殖するまでにかかる時間はどちらが長いか. →答え
《円の周りを回転する円上の動点の軌跡》 円 $C$ は半径が同じ定円 $O$ の周りをすべることなく回転している. $C$ 上の点 $\mathrm P$ が $O$ と接したときから再び $O$ と接するまで動くとき, $\mathrm P$ の軌跡が囲む領域の面積は $C$ の面積の何倍か. →答え
《ヤギの問題》平らな農場で, ヤギが円柱形の柱の一端に伸び縮みのしないひもでつながれている. ひもの長さが柱の周の長さに等しいとき, ヤギが動き回れる範囲の面積は, 柱の断面積の何倍か. ただし, ヤギの大きさ, ひもの太さとつなぎ目は考えないものとする. →答え
《パイプの共通部分の体積》前後, 左右, 上下方向に延びる内径の等しいパイプの軸が $1$ 点で直交するとき, $3$ 本のパイプの共通部分の体積は, パイプが円柱状である場合, 正四角柱である場合の何倍になるか. →答え
《タイヤの周上の点が動く長さ》タイヤの周上の $1$ 点はタイヤが $1$ 回転する間にタイヤの半径の何倍の長さを動くか. →答え
《棒の通過範囲の境界線の長さ》鉛直な壁に垂直に立てかけられた細い棒が水平な床に, 上端が壁に接したまま下端が床をすべりながら倒れた. このときの棒の通過範囲の境界線の長さは, 棒の長さの何倍か. →答え
《円の伸開線の長さ》円に伸び縮みのしないひもをたるみなく巻きつけていくと, ちょうど $1$ 周したところで巻き終わった. このとき, ひもの先端が描く曲線の長さはひもの長さの何倍か. ただし, ひもの太さは無視して考えるものとする. →答え
《放物線の長さ》動点が放物線 $y = \dfrac{x^2}{4p}$ $(p \neq 0)$ 上の $0 \leqq x \leqq b$ の範囲を動くとき, どれだけの道のりを動くか. →答え
《バクテリアの増殖》あるバクテリアの増殖率はその時点の数に比例するという. このバクテリアが $n$ 倍に増殖するまでにかかる時間と, $n$ 倍から $n^2$ 倍に増殖するまでにかかる時間はどちらが長いか. →答え
不等式
《$3$ 変数の相加・相乗平均の不等式》体積が $V$ である直方体の縦の長さ, 横の長さ, 高さの平均値と, 体積が $V$ である立方体の $1$ 辺の長さは, どちらの方が長いか. →答え
《積の和の最大値》$2$ 人 $1$ チームでゲームを行う. 全員が $1$ 番から $n$ 番までの合計 $n$ 枚の番号札を持ち, チームごとに $n$ 回に分けて $2$ 人同時に番号札を $1$ 枚ずつ場に出して, $2$ 枚の番号の積の合計をチームの得点とする. このゲームの得点として考えられる値は最大でいくらか. ただし, それぞれの番号札は $1$ 回しか使えないものとする. →答え
《積の和の最大値》$2$ 人 $1$ チームでゲームを行う. 全員が $1$ 番から $n$ 番までの合計 $n$ 枚の番号札を持ち, チームごとに $n$ 回に分けて $2$ 人同時に番号札を $1$ 枚ずつ場に出して, $2$ 枚の番号の積の合計をチームの得点とする. このゲームの得点として考えられる値は最大でいくらか. ただし, それぞれの番号札は $1$ 回しか使えないものとする. →答え
さまざまな解析学
《無理数の無理数乗》無理数の無理数乗として表される有理数は存在するか.
存在する場合にはその一例を挙げ, 存在しない場合にはその理由を説明せよ. →答え
《$2$ つの整数の整数乗が等しくなる条件》$a,$ $b$ を $1$ より大きい整数とする. $a$ を整数乗した値と $b$ を整数乗した値が等しくなるのはどのような場合か. →答え
《$2$ つの整数の整数乗が等しくなる条件》$a,$ $b$ を $1$ より大きい整数とする. $a$ を整数乗した値と $b$ を整数乗した値が等しくなるのはどのような場合か. →答え
幾何学
初等幾何学
《トリチェリーの問題》$3$ つの工場 A, B, C からなる工業地域に $1$ つの変電所を建てる.
変電所からそれぞれの工場までの送電線の長さの和が最小になるようにするには, 変電所をどのような位置に建てればよいか.
ただし, $\triangle\mathrm{ABC}$ のすべての内角は $120^\circ$ 未満であるとする.
(ヒント: 平面ベクトル $\vec v\,(\neq \vec 0),$ $\vec w$ に対して $|\vec v-\vec w| \geqq |\vec v|-\dfrac{\vec v}{|\vec v|}\cdot\vec w$ が成り立つ.) →答え
《$3$ 点からの距離の平方和が最小の点》平面において, $\triangle\mathrm{ABC}$ の $3$ 頂点からの距離の $2$ 乗の和が最小である点はどのような点か. →答え
《ナポレオンの定理》平面おいて $\triangle\mathrm{ABC}$ の外側に正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかき, それらの重心をそれぞれ $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ とおく.
$\triangle\mathrm A''\mathrm B''\mathrm C''$ はどのような形の三角形か. →答え
《レギオモンタヌスの問題》フィールドの中央から $d$ だけ離れたセンターライン上の地点から, 選手が敵陣のゴールラインに向かって真っすぐ進んでいる.
ゴールの幅が $w$ であるとき, ゴールを見込む角が最大になるという意味でシュートを放つのに最も適しているのは, ゴールラインからどれだけ離れた地点か.
ただし, $d > \dfrac{w}{2}$ とする. →答え
《正多角形の辺と対角線の長さの総和》ペンキで正 $n$ 角形の周とそのすべての対角線を描くとき, 周のみを描くときの何倍のペンキを使うか. →答え
《正七角形調和》正七角形 $\mathrm{ABCDEFG}$ の形をした公園があり, 各頂点から他の頂点に向かって真っすぐな歩道が伸びている.
B さん, C さんがそれぞれ点 $\mathrm B,$ $\mathrm C$ から点 $\mathrm G$ に向かって真っすぐに歩いたところ, 所要時間は同じになった.
A さんが B さん, C さんの平均の速さで点 $\mathrm A$ から点 $\mathrm G$ に向かって真っすぐに歩くとき, 所要時間は B さんの何倍になるか. →答え
解析幾何学
《光の照射範囲》床の上の光源 $\mathrm O$ から, 天井から垂らされたスクリーン上の点 $\mathrm C$ に向かって光を照射したところ, 真横から見て, 光はスクリーンの下端 $\mathrm A$ から上端 $\mathrm B$ にまで達し, スクリーンの真下にある床の上の点を $\mathrm H$ として $\mathrm{OH} = \mathrm{HA} = \mathrm{AC}$ となった.
このとき, 点 $\mathrm B$ の床からの距離は点 $\mathrm A$ の床からの距離の何倍になるか. →答え
《等面四面体の体積》たかし君は, $3$ 辺の長さが $a,$ $b,$ $c$ である鋭角三角形の板 $4$ 枚を貼り合わせて正四面体のオブジェを作った.
このオブジェの体積はいくらか. →答え
《オイラーの不等式》円柱に $3$ 枚の薄い長方形の板を貼り付けて三角柱を作り, これを回転させることで新しい円柱を作る.
新しい円柱の半径が最小になるようにするとき, その半径はもとの円柱の半径の何倍になるか. →答え
《三角形の外接円と内接円の半径の比》$3$ 辺の長さと面積が整数である三角形は「ヘロンの三角形」と呼ばれ, その外接円, 内接円の半径が有理数であることはよく知られている.
それでは, $3$ 辺の長さが整数である三角形において外接円の半径に対する内接円の半径の比は有理数であるという主張は正しいか.
正しければ証明を与え, 誤りであれば反例を挙げよ. →答え
《球に入る最大の正多面体》球状のカプセルにできるだけ体積の大きい正多面体の模型を入れたい.
どの正多面体の模型を入れればよいか. →答え
《三角柱の側面の勾配》三角柱のブロックを横にして平らな床で転がすと, 側面が床につく度に斜面の勾配が整数になった.
このとき, 各勾配の値はいくらか. →答え
《傾きの関係式》ある街に $3$ つの坂があり, 最も緩い坂の斜度は他の $2$ つの坂の斜度の差に等しいという.
鉛直方向に $1$ m 上るために水平方向に進まなければならない距離が最もきつい坂で $x$ m, $2$ 番目にきつい坂で $(x+1)$ m であるとき, この距離は最も緩い坂で何 m になるか. →答え
《正接の和の最小値》大きな鋭角三角形のオブジェを作る.
三角形の各頂点から反時計周りに辺に沿って $1$ だけ進んだ点から進行方向に対して垂直な方向に辺にぶつかるまで支柱を伸ばす.
$3$ 本の支柱の長さの和を最小にするには, オブジェをどうような形にすればよいか. →答え
《楕円に内接する三角形》楕円に内接する三角形について, 楕円に占める三角形の面積の割合は最大でいくらになるか. →答え
《ヘロンの公式》$3$ 辺の長さが $a,$ $b,$ $c$ である三角形の面積 $S$ はどのように表されるか. →答え
《ブラーマグプタの公式とパラメシュヴァーラの公式》
- (1)
- 円に内接し, $4$ 辺の長さが $a,$ $b,$ $c,$ $d$ である四角形の $S$ は $a,$ $b,$ $c,$ $d$ を用いてどのように表されるか.
- (2)
- $4$ 辺の長さが $a,$ $b,$ $c,$ $d$ である四角形が円に内接するとき, その半径 $R$ は $a,$ $b,$ $c,$ $d$ を用いてどのように表されるか.
(ヒント: 円に内接する四角形 $\mathrm{ABCD}$ において $\mathrm{AC}\cdot\mathrm{BD} = \mathrm{AB}\cdot\mathrm{CD}+\mathrm{BC}\cdot\mathrm{DA}$ が成り立つという「トレミーの定理」を用いる.)
→答え
《三角形の等周問題》周の長さが一定の三角形のうち面積が最大のものはどのような形の三角形か. →答え
《座標法》頂点の座標が $(x_1,y_1),$ $\cdots,$ $(x_n,y_n)$ である $n$ 角形の面積 $S$ はどのように表されるか. →答え
《棒の継ぎ目の軌跡》長さが $a,$ $b$ $(a \neq b)$ の棒を $1$ 本につなぎ, 新たな棒を作る.
これを両端が L 字型の壁を伝うように動かすとき, 棒の継ぎ目はどのような軌跡を描くか. →答え
《引きずられた荷物の軌跡》伸び縮みのしない長さ $1$ のひもの先端に荷物がくくり付けられている.
荷主が $xy$ 平面上の原点 $\mathrm O$ から $x$ 軸正方向へ荷物を引きずりながら移動するとき, 点 $(0,1)$ にあった荷物が描く軌跡はどのような式で表されるか.
$x \geqq 0$ の範囲で, 荷物が点 $\mathrm P$ にあるとき荷主が点 $\mathrm M$ にいるとして, $x$ 軸正方向と $\mathrm{MP}$ のなす角 $\theta$ を用いて表せ.
(ヒント: 点 $\mathrm P(x,y)$ における曲線の接線の傾き $\dfrac{dy}{dx}$ は直線 $\mathrm{MP}$ の傾きに等しいこと, $x$ は $y = 1$ において連続であることを利用する.) →答え
離散幾何学
《正平面充填形》平面に $1$ 種類の正多角形を隙間も重なりもなく敷き詰める方法は, 全部で何通りあるか.
ただし, 使用する正多角形はすべて同じ大きさであり, $3$ 枚以上の正多角形は頂点のみを共有する方法のみを考えるものとする. →答え
《一筆書きが可能な正多面体》正多面体のうち, すべての辺が一筆書きでなぞれるものはどれか. →答え
《正方形の頂点を結ぶ最短経路》分岐点を新たに設けてもよいとするとき, 正方形の $4$ 個の頂点を結ぶ最短経路の長さは正方形の周の長さの何倍か. →答え
《円を用いたヴェン図の限界》ある全体集合に属する集合を円で表し (集合の要素を円の内部または周上の点, 補集合の要素を円の外部の点に対応させる), 集合の共通部分を円の重なり (面積は正) で表す.
このとき, どのような集合も $1$ つの平面上に表せるのは, 集合が何個以下のときか. →答え
《楕円の周による平面の分割》$n$ 個の楕円の周により平面が分割されてできる領域の個数の最大値はいくらか. →答え
《平面における格子点を頂点とする正三角形》方眼紙において, 横方向の罫線と縦方向の罫線の交点を格子点と呼ぶ.
$3$ 個の格子点を頂点とするような正三角形は存在するか.
存在するならばその一例を挙げ, 存在しないならばその理由を述べよ. →答え
《空間における格子点を頂点とする正六角形》平面や空間において, 座標の各成分が整数である点を格子点と呼ぶ.
平面において $6$ 個の格子点を頂点とするような正六角形は存在しないことが知られている.
それでは, 空間において $6$ 個の格子点を頂点とするような正六角形は存在するか.
存在するならばそのような正六角形の $1$ 辺の長さの最小値を求め, 存在しないならばその理由を述べよ. →答え
《シュタインハウスの問題》方眼紙において, 横方向の罫線と縦方向の罫線の交点を格子点と呼ぶ.
与えられた正の整数 $n$ に対して, ちょうど $n$ 個の格子点を含むような円は存在するか.
ヒント: 点 $\left(\sqrt 2,\dfrac{1}{3}\right)$ からそれぞれの格子点までの距離を考えてみよ. →答え
《頂点と内心が格子点である鋭角三角形》$xy$ 平面において $x$ 座標も $y$ 座標も整数である点を格子点と呼ぶ.
格子点を頂点とする鋭角三角形のうち, 内心も格子点である三角形の例を挙げよ. →答え
《三角格子上の正六角形の個数》正六角形 $H$ の各辺を $n$ 等分する点をとり, そのうち $H$ の辺と平行な直線上にある $2$ 点をそれぞれ線分で結ぶ (いわゆる「三角格子」を作る).
このとき, これらの線分, または $H$ の辺, 最長対角線 (まとめて「格子線」と呼ぶ) で囲まれた正六角形は何個あるか. →答え
さまざまな幾何学
《コッホ雪片の一般化》$p$ を $3$ 以上の整数とする.
$K_0$ を正 $p$ 角形として, 多角形 $K_n$ $(n \geqq 0)$ の各辺の $3$ 等分点を隣り合う $2$ つの頂点とするような正 $p$ 角形を $K_n$ の外側に重なりを許して貼り合わせることで多角形 $K_{n+1}$ を定める.
このとき, $K_n$ ののべ面積 (重なりも加算) が有限な値に近づいていく $p$ の最大値はいくらか. →答え
組合せ論・確率論
組合せ論
《試合数》総当たりのリーグ戦の試合数, トーナメント戦で優勝チームを決めるのに必要な試合数を比較するとき, 前者が後者を上回るのは, 参加チームが何チーム以上のときか. →答え
《パスワードの作り方》$2n$ 個の文字を各文字の候補として $n$ 文字のパスワードを作る.
重複する文字がある確率が重複する文字がない確率より高くなるのは, パスワードが何文字のときか. →答え
《正多面体の塗り分け》$p = 4,$ $6,$ $8,$ $12,$ $20$ とする.
$p$ 色を使って正 $p$ 面体の各面に互いに異なる色を塗る方法はそれぞれ何通りあるか. →答え
《$6$ 本の棒を辺とする四面体の総数》長さの異なる $6$ 本の棒があり, どの $3$ 本を選んでもそれらを辺とする三角形が作れるとする.
このとき, これらの棒を辺とする四面体は何通り作れるか.
ただし, $2$ つの四面体は, 平行移動や回転移動によって重なるとき同じ四面体とみなすが, 互いに鏡像の関係にあるとき異なる四面体とみなすものとする. →答え
《公平にものを分配する方法》異なる $nr$ 個のものを $n$ 人に $r$ 個ずつ配る方法は何通りあるか. →答え
《偶数個のものを選ぶ方法》異なる $n$ 個のものから偶数個 ($2$ 個以上) のものを選ぶ方法は全部で何通りあるか. →答え
《リーグ戦で全チームの勝敗の数が異なる確率》$n$ チームが参加する総当たりのリーグ戦において, 全チームの勝敗の数が異なる確率はいくらか.
ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする. →答え
《リーグ戦で全チームが引き分ける確率》$2n+1$ チーム $(n \geqq 1)$ が参加する総当たりのリーグ戦において, 全チームが $n$ 勝 $n$ 敗で引き分ける確率はいくらか.
ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする. →答え
《正多角形の頂点を結ぶ鋭角三角形》正 $n$ 角形 $(n \geqq 3)$ の頂点を結ぶ三角形のうち, 鋭角三角形が占める割合はいくらか. →答え
《完全順列の割合》$n$ 人 $(n \geqq 2)$ の席替えで全員の席が替わる確率 $p_n$ の最大値, 最小値はいくらか (高校生向け).
また, $n$ が大きくなるにつれて $p_n$ はどのような値に近づいていくか (大学生向け). →答え
《番勝負が最終戦までもつれ込む確率》A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行うとき, 対戦が最終戦までもつれ込む確率はいくらか.
ただし, A, B の実力は互角であり, 引き分けはないとする. →答え
《番勝負でリードを許さずに優勝する場合の数と確率》A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行う.
- (A)
- A が B に $1$ 度もリードを許さずに優勝する場合の数が素数になるのは何番勝負を行ったときか.
- (B)
- A が B に $1$ 度もリードを許さずに優勝する確率はいくらか.
ただし, A, B の実力は互角であり, 引き分けはないとする. →答え
《ベルトランの投票問題》選挙で A は $a$ 票を得て, B はそれより少ない $b$ 票を得た.
投票中にずっと A の得票数が B の得票数を上回っていた確率はいくらか.
ただし, どの順序で投票されることも同様に確からしいとする. →答え
《弦の交点の個数》円に互いに平行でない $n$ 本の弦を引くとき, 交点の個数は最大でいくらになるか. →答え
《ケーキ数》A, B の $2$ 人がそれぞれ $1$ ホールのケーキを切り分ける.
A は毎回ピースを一列に並べ直してから切り, B はケーキを固定したまま切る.
できるだけ多くのピースに切り分けるとき, ピースの個数で A が B を上回るのは, 何回ナイフを入れたときか.
ただし, ナイフは空間内のどの方向にでも真っすぐに入れられるものとし, $1$ 回の入刀で切断面が通るピースをすべて切り分けるものとする. →答え
確率論
《ド・メレの $2$ つのさいころ》$1$ つのさいころを $4$ 回ふって $6$ の目が出れば勝ちというゲーム A と, $2$ つのさいころを $24$ 回ふって $6$ のぞろ目が出れば勝ちというゲーム B は, どちらの方が勝つ確率が高いか. →答え
《賞金の分配問題》$2$ 人で公平な勝負を繰り返し, 先に $3$ 回勝った方が賞金をすべてもらうというゲームを A が $2$ 勝, B が $1$ 勝の段階で中止するとき, 賞金はどのような割合で A, B に分配するべきか. →答え
《コイン投げの確率の最大値》表, 裏が等確率で出る $1$ 枚のコインがある.
これをちょうど $r$ 回表が出る確率が最大となるような回数だけ投げるとき, 何回投げればよいか. →答え
《モンティ・ホール問題》$3$ つのドア A, B, C のうち, いずれかのドアの向こうに賞品が無作為に隠されている.
挑戦者はドアを $1$ つだけ開けて, 賞品があれば, それをもらうことができる.
挑戦者がドアを選んでからドアを開けるまでの間に, 司会者は残った $2$ つのドアのうち, はずれのドアを $1$ つ無作為に開ける.
このとき, 挑戦者は開けるドアを変更することができる.
ドアを変更するとき, しないときのどちらが賞品を得る確率が高いか. →答え
《ホイヘンスの第 $2$ 問題》袋の中に赤玉が $a$ 個, 白玉が $b$ 個入っている.
あるクラスの生徒 $n$ 人が玉を $1$ 個取り出して戻すという操作を誰かが赤玉を取り出すまで出席番号順に何巡でも繰り返すとき, $k$ 番の生徒が赤玉を取り出す確率はいくらか. →答え
《$n$ 回以下のじゃんけんで順位が決まる確率》$3$ 人がじゃんけんをして, $n$ 回以下で $1$ 位から $3$ 位までの順位が決まる確率はいくらか.
ただし, $3$ 人の手の出し方は, どれも同様に確からしいとする. →答え
《誕生日が一致する確率》公転周期が $n$ 日の惑星で集会を開く.
同じ誕生日の人がいる確率が $2$ 分の $1$ 以上になるのは, この惑星の住人が何人以上集まったときか.
$x$ が十分に小さいとき近似式 $1-x \fallingdotseq e^{-x}$ ($e$: ネイピア数), $a^{x(x-1)} \fallingdotseq a^{x^2}$ $(0 < a < 1)$ が成り立つことを利用して解け. →答え
《ポリアの壺》最初, 壺の中に色 $1$ の玉が $a_1$ 個, $\cdots,$ 色 $r$ の玉が $a_r$ 個だけ入っている.
壺の中から無作為に玉を $1$ 個取り出して, その玉と同じ色の玉を $c$ 個だけ壺の中に入れ, 取り出した玉も戻すという試行を繰り返す.
$n$ 回目に色 $i$ $(1 \leqq i \leqq r)$ の玉を取り出す確率はいくらか. →答え
《破産の確率》A は $m$ 個, B は $n$ 個のあめを持っている.
$2$ 人はゲームを行い, 勝者が敗者から $1$ 個のあめをもらうという試行を, 一方のあめがなくなるまで繰り返す.
各回のゲームで A の勝率が $a,$ B の勝率が $b$ $(0 < a \leqq b < 1)$ であり, 引き分けはないとするとき, B のあめがなくなる確率はいくらか. →答え
《くじ引きのサドンデス》つぼの中に赤玉, 白玉を入れ, $2$ 人が交互に玉を $1$ 個ずつ取り出して, 先に赤玉を取り出した者を勝者とするゲームを行う.
どのように赤玉, 白玉を入れれば先手, 後手の勝率が等しくなるか.
ただし, 取り出した玉は, もとに戻さないものとする. →答え
《巴戦で優勝する確率》A, B, C の $3$ 選手が巴戦で優勝決定戦を行う.
A, B の対戦から始めて, $2$ 試合目以降は直前の試合の勝者と控えの選手が対戦し, 先に $2$ 連勝した選手を優勝とする.
$3$ 選手の実力が互角であり, 各試合で引き分けはないとするとき, A, B, C が優勝する確率の比は何対何対何か. →答え
《三角形の周上のランダム・ウォーク》正三角形 $\mathrm{ABC}$ の頂点 $\mathrm A$ にいるアリが $1$ 秒ごとに異なる頂点に等確率で移動していくとき, $n$ 秒後に頂点 $\mathrm A$ にいる確率はいくらか. →答え
《紅白まんじゅうの交換》A, B がそれぞれ紅白のまんじゅうが $1$ 個ずつ入った袋を持っている.
A, B が各自の袋からまんじゅうを $1$ 個取り出して交換して袋にしまうという操作を $n$ 回繰り返したとき, A, B がともに紅白のまんじゅうを $1$ 個ずつ持っている確率はいくらか. →答え
《テニスの勝率》A, B がテニスの試合している.
A のサービス・ゲームにおいて, A のポイント獲得率が B のポイント獲得率の $2$ 倍であるとき, デュースになった時点から A がこのゲームをとる確率はいくらか. →答え
《ポリアの壺における期待値》最初に色 $1$ の玉が $a_1$ 個, $\cdots,$ 色 $r$ の玉が $a_r$ 個だけ入っていた壺の中から無作為に玉を $1$ 個取り出して, その玉と同じ色の玉を $c$ 個だけ壺の中に入れ, 取り出した玉も戻すという試行を繰り返すとき, $n$ 回目の試行後に壺に入っている色 $i$ の玉の個数の期待値はいくらか. →答え
《じゃんけんの勝者の人数》$1$ 回だけじゃんけんをするとき, 勝者の人数が最も多くなると見込まれるのは, 何人でじゃんけんをするときか. →答え
《赤玉が出るまでに取り出す玉の個数》$r$ 個の赤玉を含む $n$ 個の玉を袋に入れる.
- (1)
- 赤玉が出るまで $1$ 個ずつ玉を取り出すとき, 何個目に赤玉を取り出すと見込まれるか.
- (2)
- すべての赤玉が出るまで $1$ 個ずつ玉を取り出すとき, 何個目に最後の赤玉を取り出すと見込まれるか.
ただし, 取り出した玉は元に戻さないものとする. →答え
《仕切り板の間にある本の冊数》$n$ 冊の本と $r$ 枚の仕切り板がある.
これらを無作為に $1$ 列に並べて空の本棚に収納するとき, 隣り合う $2$ 枚の仕切り板の間にある本は平均的に何冊になると見込まれるか. →答え
《夫婦円卓問題》$n$ 組 $(n \geqq 2)$ の夫婦 $2n$ 人が, 男女交互に, それ以外は無作為に円卓の周りに座るとき, 隣どうしに座ると見込まれる夫婦は何組か. →答え
《さいころですべての目を出すまでにかかる回数》$n$ 面のさいころがある.
すべての目を出すには, 平均的に何回さいころをふればよいと見込まれるか (ヒント: 正の整数全体を値域とする確率変数 $W$ の期待値は $E(W) = \displaystyle\sum_{m = 1}^\infty m\,P(W = m)$ で定義される). →答え
《$3$ 点からの距離の平方和が最小の点》平面において, $\triangle\mathrm{ABC}$ の $3$ 頂点からの距離の $2$ 乗の和が最小である点はどのような点か. →答え
《ナポレオンの定理》平面おいて $\triangle\mathrm{ABC}$ の外側に正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかき, それらの重心をそれぞれ $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ とおく. $\triangle\mathrm A''\mathrm B''\mathrm C''$ はどのような形の三角形か. →答え
《レギオモンタヌスの問題》フィールドの中央から $d$ だけ離れたセンターライン上の地点から, 選手が敵陣のゴールラインに向かって真っすぐ進んでいる. ゴールの幅が $w$ であるとき, ゴールを見込む角が最大になるという意味でシュートを放つのに最も適しているのは, ゴールラインからどれだけ離れた地点か. ただし, $d > \dfrac{w}{2}$ とする. →答え
《正多角形の辺と対角線の長さの総和》ペンキで正 $n$ 角形の周とそのすべての対角線を描くとき, 周のみを描くときの何倍のペンキを使うか. →答え
《正七角形調和》正七角形 $\mathrm{ABCDEFG}$ の形をした公園があり, 各頂点から他の頂点に向かって真っすぐな歩道が伸びている. B さん, C さんがそれぞれ点 $\mathrm B,$ $\mathrm C$ から点 $\mathrm G$ に向かって真っすぐに歩いたところ, 所要時間は同じになった. A さんが B さん, C さんの平均の速さで点 $\mathrm A$ から点 $\mathrm G$ に向かって真っすぐに歩くとき, 所要時間は B さんの何倍になるか. →答え
《等面四面体の体積》たかし君は, $3$ 辺の長さが $a,$ $b,$ $c$ である鋭角三角形の板 $4$ 枚を貼り合わせて正四面体のオブジェを作った. このオブジェの体積はいくらか. →答え
《オイラーの不等式》円柱に $3$ 枚の薄い長方形の板を貼り付けて三角柱を作り, これを回転させることで新しい円柱を作る. 新しい円柱の半径が最小になるようにするとき, その半径はもとの円柱の半径の何倍になるか. →答え
《三角形の外接円と内接円の半径の比》$3$ 辺の長さと面積が整数である三角形は「ヘロンの三角形」と呼ばれ, その外接円, 内接円の半径が有理数であることはよく知られている. それでは, $3$ 辺の長さが整数である三角形において外接円の半径に対する内接円の半径の比は有理数であるという主張は正しいか. 正しければ証明を与え, 誤りであれば反例を挙げよ. →答え
《球に入る最大の正多面体》球状のカプセルにできるだけ体積の大きい正多面体の模型を入れたい. どの正多面体の模型を入れればよいか. →答え
《三角柱の側面の勾配》三角柱のブロックを横にして平らな床で転がすと, 側面が床につく度に斜面の勾配が整数になった. このとき, 各勾配の値はいくらか. →答え
《傾きの関係式》ある街に $3$ つの坂があり, 最も緩い坂の斜度は他の $2$ つの坂の斜度の差に等しいという. 鉛直方向に $1$ m 上るために水平方向に進まなければならない距離が最もきつい坂で $x$ m, $2$ 番目にきつい坂で $(x+1)$ m であるとき, この距離は最も緩い坂で何 m になるか. →答え
《正接の和の最小値》大きな鋭角三角形のオブジェを作る. 三角形の各頂点から反時計周りに辺に沿って $1$ だけ進んだ点から進行方向に対して垂直な方向に辺にぶつかるまで支柱を伸ばす. $3$ 本の支柱の長さの和を最小にするには, オブジェをどうような形にすればよいか. →答え
《楕円に内接する三角形》楕円に内接する三角形について, 楕円に占める三角形の面積の割合は最大でいくらになるか. →答え
《ヘロンの公式》$3$ 辺の長さが $a,$ $b,$ $c$ である三角形の面積 $S$ はどのように表されるか. →答え
《ブラーマグプタの公式とパラメシュヴァーラの公式》
- (1)
- 円に内接し, $4$ 辺の長さが $a,$ $b,$ $c,$ $d$ である四角形の $S$ は $a,$ $b,$ $c,$ $d$ を用いてどのように表されるか.
- (2)
- $4$ 辺の長さが $a,$ $b,$ $c,$ $d$ である四角形が円に内接するとき, その半径 $R$ は $a,$ $b,$ $c,$ $d$ を用いてどのように表されるか. (ヒント: 円に内接する四角形 $\mathrm{ABCD}$ において $\mathrm{AC}\cdot\mathrm{BD} = \mathrm{AB}\cdot\mathrm{CD}+\mathrm{BC}\cdot\mathrm{DA}$ が成り立つという「トレミーの定理」を用いる.)
《三角形の等周問題》周の長さが一定の三角形のうち面積が最大のものはどのような形の三角形か. →答え
《座標法》頂点の座標が $(x_1,y_1),$ $\cdots,$ $(x_n,y_n)$ である $n$ 角形の面積 $S$ はどのように表されるか. →答え
《棒の継ぎ目の軌跡》長さが $a,$ $b$ $(a \neq b)$ の棒を $1$ 本につなぎ, 新たな棒を作る. これを両端が L 字型の壁を伝うように動かすとき, 棒の継ぎ目はどのような軌跡を描くか. →答え
《引きずられた荷物の軌跡》伸び縮みのしない長さ $1$ のひもの先端に荷物がくくり付けられている. 荷主が $xy$ 平面上の原点 $\mathrm O$ から $x$ 軸正方向へ荷物を引きずりながら移動するとき, 点 $(0,1)$ にあった荷物が描く軌跡はどのような式で表されるか. $x \geqq 0$ の範囲で, 荷物が点 $\mathrm P$ にあるとき荷主が点 $\mathrm M$ にいるとして, $x$ 軸正方向と $\mathrm{MP}$ のなす角 $\theta$ を用いて表せ. (ヒント: 点 $\mathrm P(x,y)$ における曲線の接線の傾き $\dfrac{dy}{dx}$ は直線 $\mathrm{MP}$ の傾きに等しいこと, $x$ は $y = 1$ において連続であることを利用する.) →答え
《一筆書きが可能な正多面体》正多面体のうち, すべての辺が一筆書きでなぞれるものはどれか. →答え
《正方形の頂点を結ぶ最短経路》分岐点を新たに設けてもよいとするとき, 正方形の $4$ 個の頂点を結ぶ最短経路の長さは正方形の周の長さの何倍か. →答え
《円を用いたヴェン図の限界》ある全体集合に属する集合を円で表し (集合の要素を円の内部または周上の点, 補集合の要素を円の外部の点に対応させる), 集合の共通部分を円の重なり (面積は正) で表す. このとき, どのような集合も $1$ つの平面上に表せるのは, 集合が何個以下のときか. →答え
《楕円の周による平面の分割》$n$ 個の楕円の周により平面が分割されてできる領域の個数の最大値はいくらか. →答え
《平面における格子点を頂点とする正三角形》方眼紙において, 横方向の罫線と縦方向の罫線の交点を格子点と呼ぶ. $3$ 個の格子点を頂点とするような正三角形は存在するか. 存在するならばその一例を挙げ, 存在しないならばその理由を述べよ. →答え
《空間における格子点を頂点とする正六角形》平面や空間において, 座標の各成分が整数である点を格子点と呼ぶ. 平面において $6$ 個の格子点を頂点とするような正六角形は存在しないことが知られている. それでは, 空間において $6$ 個の格子点を頂点とするような正六角形は存在するか. 存在するならばそのような正六角形の $1$ 辺の長さの最小値を求め, 存在しないならばその理由を述べよ. →答え
《シュタインハウスの問題》方眼紙において, 横方向の罫線と縦方向の罫線の交点を格子点と呼ぶ. 与えられた正の整数 $n$ に対して, ちょうど $n$ 個の格子点を含むような円は存在するか. ヒント: 点 $\left(\sqrt 2,\dfrac{1}{3}\right)$ からそれぞれの格子点までの距離を考えてみよ. →答え
《頂点と内心が格子点である鋭角三角形》$xy$ 平面において $x$ 座標も $y$ 座標も整数である点を格子点と呼ぶ. 格子点を頂点とする鋭角三角形のうち, 内心も格子点である三角形の例を挙げよ. →答え
《三角格子上の正六角形の個数》正六角形 $H$ の各辺を $n$ 等分する点をとり, そのうち $H$ の辺と平行な直線上にある $2$ 点をそれぞれ線分で結ぶ (いわゆる「三角格子」を作る). このとき, これらの線分, または $H$ の辺, 最長対角線 (まとめて「格子線」と呼ぶ) で囲まれた正六角形は何個あるか. →答え
組合せ論
《試合数》総当たりのリーグ戦の試合数, トーナメント戦で優勝チームを決めるのに必要な試合数を比較するとき, 前者が後者を上回るのは, 参加チームが何チーム以上のときか. →答え
《パスワードの作り方》$2n$ 個の文字を各文字の候補として $n$ 文字のパスワードを作る. 重複する文字がある確率が重複する文字がない確率より高くなるのは, パスワードが何文字のときか. →答え
《正多面体の塗り分け》$p = 4,$ $6,$ $8,$ $12,$ $20$ とする. $p$ 色を使って正 $p$ 面体の各面に互いに異なる色を塗る方法はそれぞれ何通りあるか. →答え
《$6$ 本の棒を辺とする四面体の総数》長さの異なる $6$ 本の棒があり, どの $3$ 本を選んでもそれらを辺とする三角形が作れるとする. このとき, これらの棒を辺とする四面体は何通り作れるか. ただし, $2$ つの四面体は, 平行移動や回転移動によって重なるとき同じ四面体とみなすが, 互いに鏡像の関係にあるとき異なる四面体とみなすものとする. →答え
《公平にものを分配する方法》異なる $nr$ 個のものを $n$ 人に $r$ 個ずつ配る方法は何通りあるか. →答え
《偶数個のものを選ぶ方法》異なる $n$ 個のものから偶数個 ($2$ 個以上) のものを選ぶ方法は全部で何通りあるか. →答え
《リーグ戦で全チームの勝敗の数が異なる確率》$n$ チームが参加する総当たりのリーグ戦において, 全チームの勝敗の数が異なる確率はいくらか. ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする. →答え
《リーグ戦で全チームが引き分ける確率》$2n+1$ チーム $(n \geqq 1)$ が参加する総当たりのリーグ戦において, 全チームが $n$ 勝 $n$ 敗で引き分ける確率はいくらか. ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする. →答え
《正多角形の頂点を結ぶ鋭角三角形》正 $n$ 角形 $(n \geqq 3)$ の頂点を結ぶ三角形のうち, 鋭角三角形が占める割合はいくらか. →答え
《完全順列の割合》$n$ 人 $(n \geqq 2)$ の席替えで全員の席が替わる確率 $p_n$ の最大値, 最小値はいくらか (高校生向け). また, $n$ が大きくなるにつれて $p_n$ はどのような値に近づいていくか (大学生向け). →答え
《番勝負が最終戦までもつれ込む確率》A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行うとき, 対戦が最終戦までもつれ込む確率はいくらか. ただし, A, B の実力は互角であり, 引き分けはないとする. →答え
《番勝負でリードを許さずに優勝する場合の数と確率》A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行う.
《ベルトランの投票問題》選挙で A は $a$ 票を得て, B はそれより少ない $b$ 票を得た. 投票中にずっと A の得票数が B の得票数を上回っていた確率はいくらか. ただし, どの順序で投票されることも同様に確からしいとする. →答え
《弦の交点の個数》円に互いに平行でない $n$ 本の弦を引くとき, 交点の個数は最大でいくらになるか. →答え
《ケーキ数》A, B の $2$ 人がそれぞれ $1$ ホールのケーキを切り分ける. A は毎回ピースを一列に並べ直してから切り, B はケーキを固定したまま切る. できるだけ多くのピースに切り分けるとき, ピースの個数で A が B を上回るのは, 何回ナイフを入れたときか. ただし, ナイフは空間内のどの方向にでも真っすぐに入れられるものとし, $1$ 回の入刀で切断面が通るピースをすべて切り分けるものとする. →答え
《パスワードの作り方》$2n$ 個の文字を各文字の候補として $n$ 文字のパスワードを作る. 重複する文字がある確率が重複する文字がない確率より高くなるのは, パスワードが何文字のときか. →答え
《正多面体の塗り分け》$p = 4,$ $6,$ $8,$ $12,$ $20$ とする. $p$ 色を使って正 $p$ 面体の各面に互いに異なる色を塗る方法はそれぞれ何通りあるか. →答え
《$6$ 本の棒を辺とする四面体の総数》長さの異なる $6$ 本の棒があり, どの $3$ 本を選んでもそれらを辺とする三角形が作れるとする. このとき, これらの棒を辺とする四面体は何通り作れるか. ただし, $2$ つの四面体は, 平行移動や回転移動によって重なるとき同じ四面体とみなすが, 互いに鏡像の関係にあるとき異なる四面体とみなすものとする. →答え
《公平にものを分配する方法》異なる $nr$ 個のものを $n$ 人に $r$ 個ずつ配る方法は何通りあるか. →答え
《偶数個のものを選ぶ方法》異なる $n$ 個のものから偶数個 ($2$ 個以上) のものを選ぶ方法は全部で何通りあるか. →答え
《リーグ戦で全チームの勝敗の数が異なる確率》$n$ チームが参加する総当たりのリーグ戦において, 全チームの勝敗の数が異なる確率はいくらか. ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする. →答え
《リーグ戦で全チームが引き分ける確率》$2n+1$ チーム $(n \geqq 1)$ が参加する総当たりのリーグ戦において, 全チームが $n$ 勝 $n$ 敗で引き分ける確率はいくらか. ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする. →答え
《正多角形の頂点を結ぶ鋭角三角形》正 $n$ 角形 $(n \geqq 3)$ の頂点を結ぶ三角形のうち, 鋭角三角形が占める割合はいくらか. →答え
《完全順列の割合》$n$ 人 $(n \geqq 2)$ の席替えで全員の席が替わる確率 $p_n$ の最大値, 最小値はいくらか (高校生向け). また, $n$ が大きくなるにつれて $p_n$ はどのような値に近づいていくか (大学生向け). →答え
《番勝負が最終戦までもつれ込む確率》A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行うとき, 対戦が最終戦までもつれ込む確率はいくらか. ただし, A, B の実力は互角であり, 引き分けはないとする. →答え
《番勝負でリードを許さずに優勝する場合の数と確率》A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行う.
- (A)
- A が B に $1$ 度もリードを許さずに優勝する場合の数が素数になるのは何番勝負を行ったときか.
- (B)
- A が B に $1$ 度もリードを許さずに優勝する確率はいくらか.
《ベルトランの投票問題》選挙で A は $a$ 票を得て, B はそれより少ない $b$ 票を得た. 投票中にずっと A の得票数が B の得票数を上回っていた確率はいくらか. ただし, どの順序で投票されることも同様に確からしいとする. →答え
《弦の交点の個数》円に互いに平行でない $n$ 本の弦を引くとき, 交点の個数は最大でいくらになるか. →答え
《ケーキ数》A, B の $2$ 人がそれぞれ $1$ ホールのケーキを切り分ける. A は毎回ピースを一列に並べ直してから切り, B はケーキを固定したまま切る. できるだけ多くのピースに切り分けるとき, ピースの個数で A が B を上回るのは, 何回ナイフを入れたときか. ただし, ナイフは空間内のどの方向にでも真っすぐに入れられるものとし, $1$ 回の入刀で切断面が通るピースをすべて切り分けるものとする. →答え
確率論
《ド・メレの $2$ つのさいころ》$1$ つのさいころを $4$ 回ふって $6$ の目が出れば勝ちというゲーム A と, $2$ つのさいころを $24$ 回ふって $6$ のぞろ目が出れば勝ちというゲーム B は, どちらの方が勝つ確率が高いか. →答え
《賞金の分配問題》$2$ 人で公平な勝負を繰り返し, 先に $3$ 回勝った方が賞金をすべてもらうというゲームを A が $2$ 勝, B が $1$ 勝の段階で中止するとき, 賞金はどのような割合で A, B に分配するべきか. →答え
《コイン投げの確率の最大値》表, 裏が等確率で出る $1$ 枚のコインがある. これをちょうど $r$ 回表が出る確率が最大となるような回数だけ投げるとき, 何回投げればよいか. →答え
《モンティ・ホール問題》$3$ つのドア A, B, C のうち, いずれかのドアの向こうに賞品が無作為に隠されている. 挑戦者はドアを $1$ つだけ開けて, 賞品があれば, それをもらうことができる. 挑戦者がドアを選んでからドアを開けるまでの間に, 司会者は残った $2$ つのドアのうち, はずれのドアを $1$ つ無作為に開ける. このとき, 挑戦者は開けるドアを変更することができる. ドアを変更するとき, しないときのどちらが賞品を得る確率が高いか. →答え
《ホイヘンスの第 $2$ 問題》袋の中に赤玉が $a$ 個, 白玉が $b$ 個入っている. あるクラスの生徒 $n$ 人が玉を $1$ 個取り出して戻すという操作を誰かが赤玉を取り出すまで出席番号順に何巡でも繰り返すとき, $k$ 番の生徒が赤玉を取り出す確率はいくらか. →答え
《$n$ 回以下のじゃんけんで順位が決まる確率》$3$ 人がじゃんけんをして, $n$ 回以下で $1$ 位から $3$ 位までの順位が決まる確率はいくらか. ただし, $3$ 人の手の出し方は, どれも同様に確からしいとする. →答え
《誕生日が一致する確率》公転周期が $n$ 日の惑星で集会を開く. 同じ誕生日の人がいる確率が $2$ 分の $1$ 以上になるのは, この惑星の住人が何人以上集まったときか. $x$ が十分に小さいとき近似式 $1-x \fallingdotseq e^{-x}$ ($e$: ネイピア数), $a^{x(x-1)} \fallingdotseq a^{x^2}$ $(0 < a < 1)$ が成り立つことを利用して解け. →答え
《ポリアの壺》最初, 壺の中に色 $1$ の玉が $a_1$ 個, $\cdots,$ 色 $r$ の玉が $a_r$ 個だけ入っている. 壺の中から無作為に玉を $1$ 個取り出して, その玉と同じ色の玉を $c$ 個だけ壺の中に入れ, 取り出した玉も戻すという試行を繰り返す. $n$ 回目に色 $i$ $(1 \leqq i \leqq r)$ の玉を取り出す確率はいくらか. →答え
《破産の確率》A は $m$ 個, B は $n$ 個のあめを持っている. $2$ 人はゲームを行い, 勝者が敗者から $1$ 個のあめをもらうという試行を, 一方のあめがなくなるまで繰り返す. 各回のゲームで A の勝率が $a,$ B の勝率が $b$ $(0 < a \leqq b < 1)$ であり, 引き分けはないとするとき, B のあめがなくなる確率はいくらか. →答え
《くじ引きのサドンデス》つぼの中に赤玉, 白玉を入れ, $2$ 人が交互に玉を $1$ 個ずつ取り出して, 先に赤玉を取り出した者を勝者とするゲームを行う. どのように赤玉, 白玉を入れれば先手, 後手の勝率が等しくなるか. ただし, 取り出した玉は, もとに戻さないものとする. →答え
《巴戦で優勝する確率》A, B, C の $3$ 選手が巴戦で優勝決定戦を行う. A, B の対戦から始めて, $2$ 試合目以降は直前の試合の勝者と控えの選手が対戦し, 先に $2$ 連勝した選手を優勝とする. $3$ 選手の実力が互角であり, 各試合で引き分けはないとするとき, A, B, C が優勝する確率の比は何対何対何か. →答え
《三角形の周上のランダム・ウォーク》正三角形 $\mathrm{ABC}$ の頂点 $\mathrm A$ にいるアリが $1$ 秒ごとに異なる頂点に等確率で移動していくとき, $n$ 秒後に頂点 $\mathrm A$ にいる確率はいくらか. →答え
《紅白まんじゅうの交換》A, B がそれぞれ紅白のまんじゅうが $1$ 個ずつ入った袋を持っている. A, B が各自の袋からまんじゅうを $1$ 個取り出して交換して袋にしまうという操作を $n$ 回繰り返したとき, A, B がともに紅白のまんじゅうを $1$ 個ずつ持っている確率はいくらか. →答え
《テニスの勝率》A, B がテニスの試合している. A のサービス・ゲームにおいて, A のポイント獲得率が B のポイント獲得率の $2$ 倍であるとき, デュースになった時点から A がこのゲームをとる確率はいくらか. →答え
《ポリアの壺における期待値》最初に色 $1$ の玉が $a_1$ 個, $\cdots,$ 色 $r$ の玉が $a_r$ 個だけ入っていた壺の中から無作為に玉を $1$ 個取り出して, その玉と同じ色の玉を $c$ 個だけ壺の中に入れ, 取り出した玉も戻すという試行を繰り返すとき, $n$ 回目の試行後に壺に入っている色 $i$ の玉の個数の期待値はいくらか. →答え
《じゃんけんの勝者の人数》$1$ 回だけじゃんけんをするとき, 勝者の人数が最も多くなると見込まれるのは, 何人でじゃんけんをするときか. →答え
《赤玉が出るまでに取り出す玉の個数》$r$ 個の赤玉を含む $n$ 個の玉を袋に入れる.
《仕切り板の間にある本の冊数》$n$ 冊の本と $r$ 枚の仕切り板がある. これらを無作為に $1$ 列に並べて空の本棚に収納するとき, 隣り合う $2$ 枚の仕切り板の間にある本は平均的に何冊になると見込まれるか. →答え
《夫婦円卓問題》$n$ 組 $(n \geqq 2)$ の夫婦 $2n$ 人が, 男女交互に, それ以外は無作為に円卓の周りに座るとき, 隣どうしに座ると見込まれる夫婦は何組か. →答え
《さいころですべての目を出すまでにかかる回数》$n$ 面のさいころがある. すべての目を出すには, 平均的に何回さいころをふればよいと見込まれるか (ヒント: 正の整数全体を値域とする確率変数 $W$ の期待値は $E(W) = \displaystyle\sum_{m = 1}^\infty m\,P(W = m)$ で定義される). →答え
《賞金の分配問題》$2$ 人で公平な勝負を繰り返し, 先に $3$ 回勝った方が賞金をすべてもらうというゲームを A が $2$ 勝, B が $1$ 勝の段階で中止するとき, 賞金はどのような割合で A, B に分配するべきか. →答え
《コイン投げの確率の最大値》表, 裏が等確率で出る $1$ 枚のコインがある. これをちょうど $r$ 回表が出る確率が最大となるような回数だけ投げるとき, 何回投げればよいか. →答え
《モンティ・ホール問題》$3$ つのドア A, B, C のうち, いずれかのドアの向こうに賞品が無作為に隠されている. 挑戦者はドアを $1$ つだけ開けて, 賞品があれば, それをもらうことができる. 挑戦者がドアを選んでからドアを開けるまでの間に, 司会者は残った $2$ つのドアのうち, はずれのドアを $1$ つ無作為に開ける. このとき, 挑戦者は開けるドアを変更することができる. ドアを変更するとき, しないときのどちらが賞品を得る確率が高いか. →答え
《ホイヘンスの第 $2$ 問題》袋の中に赤玉が $a$ 個, 白玉が $b$ 個入っている. あるクラスの生徒 $n$ 人が玉を $1$ 個取り出して戻すという操作を誰かが赤玉を取り出すまで出席番号順に何巡でも繰り返すとき, $k$ 番の生徒が赤玉を取り出す確率はいくらか. →答え
《$n$ 回以下のじゃんけんで順位が決まる確率》$3$ 人がじゃんけんをして, $n$ 回以下で $1$ 位から $3$ 位までの順位が決まる確率はいくらか. ただし, $3$ 人の手の出し方は, どれも同様に確からしいとする. →答え
《誕生日が一致する確率》公転周期が $n$ 日の惑星で集会を開く. 同じ誕生日の人がいる確率が $2$ 分の $1$ 以上になるのは, この惑星の住人が何人以上集まったときか. $x$ が十分に小さいとき近似式 $1-x \fallingdotseq e^{-x}$ ($e$: ネイピア数), $a^{x(x-1)} \fallingdotseq a^{x^2}$ $(0 < a < 1)$ が成り立つことを利用して解け. →答え
《ポリアの壺》最初, 壺の中に色 $1$ の玉が $a_1$ 個, $\cdots,$ 色 $r$ の玉が $a_r$ 個だけ入っている. 壺の中から無作為に玉を $1$ 個取り出して, その玉と同じ色の玉を $c$ 個だけ壺の中に入れ, 取り出した玉も戻すという試行を繰り返す. $n$ 回目に色 $i$ $(1 \leqq i \leqq r)$ の玉を取り出す確率はいくらか. →答え
《破産の確率》A は $m$ 個, B は $n$ 個のあめを持っている. $2$ 人はゲームを行い, 勝者が敗者から $1$ 個のあめをもらうという試行を, 一方のあめがなくなるまで繰り返す. 各回のゲームで A の勝率が $a,$ B の勝率が $b$ $(0 < a \leqq b < 1)$ であり, 引き分けはないとするとき, B のあめがなくなる確率はいくらか. →答え
《くじ引きのサドンデス》つぼの中に赤玉, 白玉を入れ, $2$ 人が交互に玉を $1$ 個ずつ取り出して, 先に赤玉を取り出した者を勝者とするゲームを行う. どのように赤玉, 白玉を入れれば先手, 後手の勝率が等しくなるか. ただし, 取り出した玉は, もとに戻さないものとする. →答え
《巴戦で優勝する確率》A, B, C の $3$ 選手が巴戦で優勝決定戦を行う. A, B の対戦から始めて, $2$ 試合目以降は直前の試合の勝者と控えの選手が対戦し, 先に $2$ 連勝した選手を優勝とする. $3$ 選手の実力が互角であり, 各試合で引き分けはないとするとき, A, B, C が優勝する確率の比は何対何対何か. →答え
《三角形の周上のランダム・ウォーク》正三角形 $\mathrm{ABC}$ の頂点 $\mathrm A$ にいるアリが $1$ 秒ごとに異なる頂点に等確率で移動していくとき, $n$ 秒後に頂点 $\mathrm A$ にいる確率はいくらか. →答え
《紅白まんじゅうの交換》A, B がそれぞれ紅白のまんじゅうが $1$ 個ずつ入った袋を持っている. A, B が各自の袋からまんじゅうを $1$ 個取り出して交換して袋にしまうという操作を $n$ 回繰り返したとき, A, B がともに紅白のまんじゅうを $1$ 個ずつ持っている確率はいくらか. →答え
《テニスの勝率》A, B がテニスの試合している. A のサービス・ゲームにおいて, A のポイント獲得率が B のポイント獲得率の $2$ 倍であるとき, デュースになった時点から A がこのゲームをとる確率はいくらか. →答え
《ポリアの壺における期待値》最初に色 $1$ の玉が $a_1$ 個, $\cdots,$ 色 $r$ の玉が $a_r$ 個だけ入っていた壺の中から無作為に玉を $1$ 個取り出して, その玉と同じ色の玉を $c$ 個だけ壺の中に入れ, 取り出した玉も戻すという試行を繰り返すとき, $n$ 回目の試行後に壺に入っている色 $i$ の玉の個数の期待値はいくらか. →答え
《じゃんけんの勝者の人数》$1$ 回だけじゃんけんをするとき, 勝者の人数が最も多くなると見込まれるのは, 何人でじゃんけんをするときか. →答え
《赤玉が出るまでに取り出す玉の個数》$r$ 個の赤玉を含む $n$ 個の玉を袋に入れる.
- (1)
- 赤玉が出るまで $1$ 個ずつ玉を取り出すとき, 何個目に赤玉を取り出すと見込まれるか.
- (2)
- すべての赤玉が出るまで $1$ 個ずつ玉を取り出すとき, 何個目に最後の赤玉を取り出すと見込まれるか.
《仕切り板の間にある本の冊数》$n$ 冊の本と $r$ 枚の仕切り板がある. これらを無作為に $1$ 列に並べて空の本棚に収納するとき, 隣り合う $2$ 枚の仕切り板の間にある本は平均的に何冊になると見込まれるか. →答え
《夫婦円卓問題》$n$ 組 $(n \geqq 2)$ の夫婦 $2n$ 人が, 男女交互に, それ以外は無作為に円卓の周りに座るとき, 隣どうしに座ると見込まれる夫婦は何組か. →答え
《さいころですべての目を出すまでにかかる回数》$n$ 面のさいころがある. すべての目を出すには, 平均的に何回さいころをふればよいと見込まれるか (ヒント: 正の整数全体を値域とする確率変数 $W$ の期待値は $E(W) = \displaystyle\sum_{m = 1}^\infty m\,P(W = m)$ で定義される). →答え
書籍
数学クイズの制作のご依頼は, 以下の連絡先までお願いいたします.
- 氏 名
- 廣津 孝 (ひろつ たかし)
- メール