コインを $n$ 回投げて $r$ 回表が出る確率を $p_n$ とおく. $$\begin{aligned} \frac{p_{n+1}}{p_n} &= \frac{{}_{n+1}\mathrm C_r\left(\dfrac{1}{2}\right) ^r\left(\dfrac{1}{2}\right) ^{n+1-r}}{{}_n\mathrm C_r\left(\dfrac{1}{2}\right) ^r\left(\dfrac{1}{2}\right) ^{n-r}} \\ &= \frac{1}{2}\cdot\frac{(n+1)!}{r!(n+1-r)!}\div\frac{n!}{r!(n-r)!} \\ &= \frac{n+1}{2(n+1-r)} \end{aligned}$$ であるから, $$\begin{aligned} p_{n+1} > p_n &\iff \frac{p_{n+1}}{p_n} > 1 \\ &\iff \frac{n+1}{2(n+1-r)} > 1 \\ &\iff n+1 > 2(n+1-r) \\ &\iff n < 2r-1, \\ p_{n+1} = p_n &\iff n = 2r-1, \\ p_{n+1} < p_n &\iff n > 2r-1 \end{aligned}$$ が成り立つ. よって, $$p_1 < \cdots < p_{2r-1} = p_{2r} > p_{2r+1} > \cdots$$ であるから, $p_n$ は $n = 2r-1,$ $2r$ のとき最大となる.

　ドア A, B, C の向こうに賞品があるという事象をそれぞれ $A,$ $B,$ $C$ とおく. さらに, 挑戦者が A を選んだとき, 司会者が C を開けるという事象を $E$ とおく. 司会者が C を開けたとき, A が当たりである条件付き確率 $P_E(A),$ B が当たりである条件付き確率 $P_E(B)$ の大小を比較すればよい.

(1)

まず, $P(E)$ を求める. 賞品は無作為に隠されているから, $$P(A) = P(B) = P(C) = \frac{1}{3}$$ である.

• A が当たりのとき司会者は C の他に B も開けることができるから, $P_A(E) = \dfrac{1}{2}$ であり, $$P(A\cap E) = P(A)P_A(E) = \frac{1}{3}\cdot\dfrac{1}{2} = \frac{1}{6} \quad \cdots [1]$$ である.
• B が当たりのとき司会者は C を開けるしかないから, $P_B(E) = 1$ であり, $$P(B\cap E) = P(B)P_B(E) = \frac{1}{3}\cdot 1 = \frac{1}{3} \quad \cdots [2]$$ である.
• C が当たりのとき司会者は C を開けることはないから, $P_C(E) = 0$ であり, $$P(C\cap E) = P(C)P_C(E) = \frac{1}{3}\cdot 0 = 0$$ である.

よって, $$\begin{aligned} P(E) &= P(A\cap E)+P(B\cap E)+P(C\cap E) \\ &= \frac{1}{6}+\frac{1}{3}+0 = \frac{1}{2} \end{aligned}$$ である.

(2)

次に, $P_E(A),$ $P_E(B)$ の各値を求めて比較する.

• $[1]$ から, $$P_E(A) = \frac{P(A\cap E)}{P(E)} = \frac{1}{6}\div\frac{1}{2} = \frac{1}{3}$$ である.
• $[2]$ から, $$P_E(B) = \frac{P(B\cap E)}{P(E)} = \frac{1}{3}\div\frac{1}{2} = \frac{2}{3}$$ である.

$P_E(A) < P_E(B)$ であるから, ドアを変更するときの方が賞品を得る確率が高い.

　$k$ 番の生徒が赤玉を取り出す確率を $p_k$ とおき, $$\alpha = \frac{a}{a+b}, \quad \beta = \frac{b}{a+b}$$ とおく.

(i)

最初に $1$ 番の生徒が赤玉を取り出すとき. その確率は $\alpha$ である.

(ii)

最初に $1$ 番の生徒が白玉を取り出すとき. $1$ 番の生徒は $2$ 番の生徒から始めたときの $n$ 番目と見なせるから, $1$ 番の生徒が赤玉を取り出す確率は $\beta p_n$ である.

よって, $$p_1 = \alpha +\beta p_n \quad \cdots [1]$$ が成り立つ. また, $k \geqq 2$ のとき, $k$ 番の生徒が赤玉を取り出すには $1$ 番の生徒が白玉を取り出すことが必要であり, $k$ 番の生徒は $2$ 番の生徒から始めたときの $k-1$ 番目と見なせるから, $$p_k = \beta p_{k-1} \quad \cdots [2]$$ である. よって, 数列 $\{ p_k\}$ は公比 $\beta$ の等比数列であるから, $$p_k = p_1\beta ^{k-1} \quad (1 \leqq k \leqq n) \quad \cdots [3]$$ が成り立つ. $p_n = p_1\beta ^{n-1}$ を $[1]$ に代入すると,

$p_1 = \alpha +p_1\beta ^n$　よって　$p_1 = \dfrac{\alpha}{1-\beta ^n}$

となる. これを $[3]$ に代入すると, $$\begin{aligned} p_k &= \frac{\alpha\beta ^{k-1}}{1-\beta ^n} \\ &= \frac{a}{a+b}\cdot\frac{b^{k-1}}{(a+b)^{k-1}}\div\left\{ 1-\frac{b^n}{(a+b)^n}\right\} \\ &= \frac{ab^{k-1}(a+b)^{n-k}}{(a+b)^n-b^n} \end{aligned}$$ が得られる.

　集会の参加者が $r$ 人であるとする. この中に同じ誕生日の人がいない確率は $$\begin{aligned} &\frac{n-1}{n}\cdot\frac{n-2}{n}\cdot\cdots\cdot\frac{n-(r-1)}{n} \\ &= \left( 1-\frac{1}{n}\right)\left( 1-\frac{2}{n}\right)\cdots\left( 1-\frac{r-1}{n}\right) \\ &\fallingdotseq e^{-\frac{1}{n}}e^{-\frac{2}{n}}\cdots e^{-\frac{r-1}{n}} \\ &= e^{-\frac{1+2+\cdots +(r-1)}{n}} = e^{-\frac{r(r-1)}{2n}} \\ &\fallingdotseq e^{-\frac{r^2}{2n}} \end{aligned}$$ であるから, 同じ誕生日の人がいる確率はおよそ $$1-e^{-\frac{r^2}{2n}}$$ である. この値が $\dfrac{1}{2}$ 以上になる条件は, $$\begin{aligned} 1-e^{-\frac{r^2}{2n}} &\geqq \frac{1}{2} \\ e^{-\frac{r^2}{2n}} &\leqq \frac{1}{2} \\ -\frac{r^2}{2n} &\leqq \log\frac{1}{2} = -\log 2 \\ r^2 &\geqq 2\log 2\cdot n \\ r &\geqq \sqrt{2\log 2}\sqrt n \end{aligned}$$ である.

　$n$ 回目に色 $i$ $(1 \leqq i \leqq r)$ の玉を取り出す確率を $p_n$ とおく. $$p_n = \frac{a_i}{a_1+\cdots +a_r} \quad \cdots [*]$$ であることを数学的帰納法で示す.

(i)

$n = 1$ のとき. 明らかに $[*]$ が成り立つ.

(ii)

$n = k$ ($k$: 正の整数) のとき $[*]$ が成り立つとする. また, $k$ 回目の試行を行う直前の壺の中にある色 $i$ の玉の個数を $x,$ その他の色の玉の個数を $y$ とおく. $k$ 回目に取り出す玉の色で場合に分けて考えると, $$\begin{aligned} p_{k+1} &= p_k\cdot\frac{x+c}{x+y+c}+(1-p_k)\cdot\frac{x}{x+y+c} \\ &= \frac{x}{x+y}\cdot\frac{x+c}{x+y+c}+\frac{y}{x+y}\cdot\frac{x}{x+y+c} \\ &= \frac{x(x+y+c)}{(x+y)(x+y+c)} = \frac{x}{x+y} \\ &= p_k = \frac{a_i}{a_1+\cdots +a_r} \end{aligned}$$ が得られる. よって, $n = k+1$ のとき $[*]$ が成り立つ.

(i), (ii) から, すべての正の整数 $n$ に対して $p_n = \dfrac{a_i}{a_1+\cdots +a_r}$ が成り立つ.

　B のあめが $k$ 個になったときに最終的に B のあめがなくなる確率を $p_k$ とおく. B のあめが $k$ 個 $(k \geqq 1)$ のとき, 確率 $a$ でゲームに負けてあめが $k-1$ 個になり, 確率 $b$ でゲームに勝ってあめが $k+1$ 個になるから, $$p_k = ap_{k-1}+bp_{k+1} \quad \cdots [*]$$ が成り立つ.

(i)

$a = b$ のとき. $[*]$ に $a = b = \dfrac{1}{2}$ を代入して整理すると $$p_{k+1}-2p_k+p_{k-1} = 0$$ となる. よって, $$p_{k+1}-p_k = p_k-p_{k-1} \quad (k \geqq 1)$$ が成り立つので, $\{ p_k\}$ は等差数列である. $p_0 = 1,$ $p_{m+n} = 0$ であるから, その公差は $c = -\dfrac{1}{m+n}$ である. ゆえに, 求める確率は $$p_n = p_0+cn = 1-\frac{n}{m+n} = \frac{m}{m+n}$$ である.

(ii)

$a < b$ のとき. $[*]$ を整理すると $$p_{k+1}-\frac{1}{b}p_k+\frac{a}{b}p_{k-1} = 0$$ となる. よって, $$p_{k+1}-p_k = \frac{a}{b}(p_k-p_{k-1}) \quad (k \geqq 1)$$ が成り立つので, $\{ p_{k+1}-p_k\}$ は第 $0$ 項 $c,$ 公比 $\dfrac{a}{b}$ の等比数列であり, その一般項は $$p_{k+1}-p_k = c\left(\frac{a}{b}\right) ^k$$ である. したがって, $$\begin{aligned} 0 &= p_{m+n} = p_0+\sum_{k = 0}^{m+n-1}c\left(\frac{a}{b}\right) ^k = 1+c\cdot\frac{1-\dfrac{a^{m+n}}{b^{m+n}}}{1-\dfrac{a}{b}} \\ c &= -\frac{1-\dfrac{a}{b}}{1-\dfrac{a^{m+n}}{b^{m+n}}} \end{aligned}$$ である. ゆえに, 求める確率は $$\begin{aligned} p_n &= p_0+\sum_{k = 0}^{n-1}c\left(\frac{a}{b}\right) ^k = 1-\frac{1-\dfrac{a}{b}}{1-\dfrac{a^{m+n}}{b^{m+n}}}\cdot\frac{1-\dfrac{a^n}{b^n}}{1-\dfrac{a}{b}} \\ &= 1-\frac{b^{m+n}-a^nb^m}{b^{m+n}-a^{m+n}} = \frac{a^n(b^m-a^m)}{b^{m+n}-a^{m+n}} \end{aligned}$$ である.

　赤玉の個数を $r,$ 白玉の個数を $s$ とおき, 先手が勝つ確率を $P(A),$ 後手が勝つ確率を $P(B)$ とおく. ちょうど $k$ 回目 (つまり $2$ 人の取り出した玉の合計がちょうど $k$ 個になったとき) に勝者が決まる確率を $p_k$ とおく.

(1)

$P(A),$ $P(B)$ を $p_k$ $(1 \leqq k \leqq s+1)$ で表す. $s$ 個より多く玉を取り出すと必ず赤玉が出るから, $s$ が偶数のとき $$\begin{aligned} P(A) &= p_1+p_3+\cdots +p_{s-1}+p_{s+1}, \\ P(B) &= p_2+p_4+\cdots +p_s \end{aligned}$$ が, $s$ が奇数のとき $$\begin{aligned} P(A) &= p_1+p_3+\cdots +p_s, \\ P(B) &= p_2+p_4+\cdots +p_{s+1} \end{aligned}$$ が成り立つ.

(2)

$p_k \geqq p_{k+1}$ が成り立つことを示す. $k$ 回目に勝者が決まらない確率を $q_k$ とおくと, $$\begin{aligned} p_{k+1} &= q_k\cdot\frac{r}{r+s-k} \quad \cdots [1], \\ q_{k+1} &= q_k\cdot\frac{s-k}{r+s-k} \end{aligned}$$ となり, $$\begin{aligned} p_{k+2} &= q_{k+1}\cdot\frac{r}{r+s-k-1} \\ &= q_k\cdot\frac{s-k}{r+s-k}\cdot\frac{r}{r+s-k-1} \quad \cdots [2] \end{aligned}$$ となる. $[1],$ $[2]$ の辺々を割ると $$\frac{p_{k+1}}{p_{k+2}} = \frac{r+s-k-1}{s-k}$$ が得られる. 一方, $r \geqq 1$ から $r+s-k-1 \geqq s-k$ であるので, $\dfrac{p_{k+1}}{p_{k+2}} \geqq 1$ つまり $p_{k+1} \geqq p_{k+2}$ が成り立つ. また, $$p_1 = \frac{r}{r+s}, \quad p_2 = \frac{s}{r+s}\cdot\frac{r}{r+s-1} = p_1\cdot\frac{s}{r+s-1}$$ から $p_1 \geqq p_2$ であるので, $p_k \geqq p_{k+1}$ が成り立つ.

(3)

$P(A) = P(B)$ となる条件を求める. (1) のいずれの場合にも, $p_1 \geqq p_2,$ $p_3 \geqq p_4,$ $\cdots$ から, $P(A) \geqq P(B)$ が成り立つ. よって, $P(A)+P(B) = 1$ から $$2P(A) \geqq P(A)+P(B) = 1$$ であるので, $P(A) \geqq \dfrac{1}{2}$ が成り立つ. $p_{s+1} \neq 0$ に注意すると, この等号が成り立つためには, $p_1 = p_2$ かつ $s$ が奇数であることが必要である. $p_1 = p_2$ のとき, $p_1 = p_1\cdot\dfrac{s}{r+s-1}$ から, $r = 1$ が成り立つ. 逆に, $r = 1$ かつ $s$ が奇数であるとき $P(A) = P(B)$ となるので, 求める条件は “$r = 1$ かつ $s$ は奇数” である.

　まんじゅうを交換する操作を $n$ 回 $(n \geqq 0)$ 行った後に, A が紅色 $1$ 個, 白色 $1$ 個を持っている確率を $m_n$ (m: mixed-color), 紅色 $2$ 個を持っている確率を $r_n$ (r: red), 白色 $2$ 個を持っている確率を $w_n$ (w: white) とおく. このとき, $$m_0 = 1, \quad r_0 = w_0 = 0$$ であり, A, B がともに紅色 $1$ 個, 白色 $1$ 個を持っている状態からは, $$\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{2} = \frac{1}{2}$$ の確率で同じ状態になり, $$\frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4}$$ の確率で A が紅色 $2$ 個, B が白色 $2$ 個の状態になり, これと同じ確率で A が白色 $2$ 個, B が紅色 $2$ 個の状態になる. また, A が紅色 $2$ 個, B が白色 $2$ 個の状態, および A が白色 $2$ 個, B が紅色 $2$ 個の状態からは, 必ず A, B がともに紅色 $1$ 個, 白色 $1$ 個を持っている状態になる (下図). 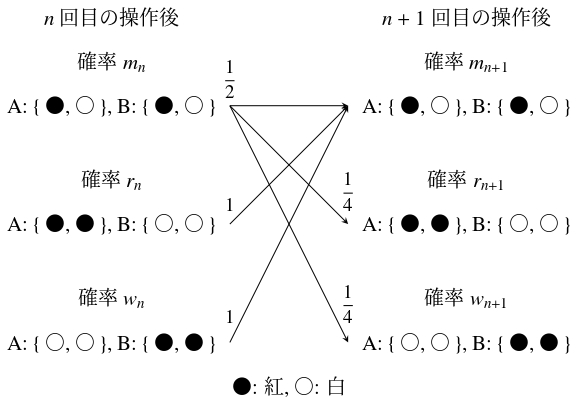よって, $$\begin{aligned} &m_{n+1} = \frac{1}{2}m_n+r_n+w_n \quad \cdots [1], \\ &r_{n+1} = w_{n+1} = \frac{1}{4}m_n \quad \cdots [2] \end{aligned}$$ が成り立つ. また, $$m_n+r_n+w_n = 1$$ であるので, $[1]$ から $r_n,$ $w_n$ を消去すると $$m_{n+1} = \frac{1}{2}m_n+(1-m_n)$$ つまり $$m_{n+1} = 1-\frac{1}{2}m_n \quad \cdots [3]$$ が得られる. $[3]$ の辺々から $$\alpha = 1-\frac{1}{2}\alpha$$ の解 $\alpha = \dfrac{2}{3}$ を引くと $$m_{n+1}-\frac{2}{3} = -\frac{1}{2}\left( m_n-\frac{2}{3}\right)$$ となるから, 数列 $\left\{ m_n-\dfrac{2}{3}\right\}$ は第 $0$ 項 $m_0-\dfrac{2}{3} = \dfrac{1}{3},$ 公比 $-\dfrac{1}{2}$ の等比数列である. ゆえに, $$m_n-\frac{2}{3} = \frac{1}{3}\left( -\frac{1}{2}\right) ^n$$ つまり $$m_n = \frac{2}{3}+\frac{1}{3}\left( -\frac{1}{2}\right) ^n \quad \cdots [4]$$ である. ちなみに, $[2]$ から $r_n = w_n = \dfrac{1}{4}m_{n-1}$ $(n \geqq 1)$ であるので, $[4]$ により $$r_n = w_n = \frac{1}{6}+\frac{1}{12}\left( -\frac{1}{2}\right) ^{n-1} = \frac{1}{6}-\frac{1}{6}\left( -\frac{1}{2}\right) ^n$$ である (これは $n = 0$ のときも成り立つ).

　$n$ を $2$ 以上の整数とする. $n$ 人で $1$ 回だけじゃんけんをするとき, 勝者の人数を $X_n$ とおく. 求めるべきは, $X_n$ の期待値 $E(X_n)$ を最大にする $n$ の値である.

(1)

まず, 勝者が $k$ 人 $(1 \leqq k \leqq n-1)$ である確率 $P(X_n = k)$ を求める. $n$ 人のじゃんけんで, 全員の手の出し方は $3^n$ 通りある. 勝者が $k$ 人 $(1 \leqq k \leqq n-1)$ であるとき, 勝者と敗者を分ける方法が ${}_n\mathrm C_k$ 通りあり, そのおのおのに対して勝者と敗者の手の組合せが ${}_3\mathrm C_2$ 通りあるから, $X_n = k$ となる確率は $$P(X_n = k) = \frac{{}_n\mathrm C_k\cdot {}_3\mathrm C_2}{3^n} = \frac{{}_n\mathrm C_k}{3^{n-1}} \quad \cdots [1]$$ である.

(2)

次に, $X_n$ の期待値 $E(X_n)$ を求める. $X_n$ は $0$ 以上 $n-1$ 以下の整数の値をとるから, $[1]$ により, $X_n$ の期待値は $$\begin{aligned} E(X_n) &= \sum_{k = 0}^{n-1}kP(X_n = k) \\ &= \sum_{k = 1}^{n-1}kP(X_n = k) \quad (\because 0\cdot P(X_n = 0) = 0) \\ &= \sum_{k = 1}^{n-1}k\cdot\frac{{}_n\mathrm C_k}{3^{n-1}} \quad (\because [1]) \\ &= \sum_{k = 1}^{n-1}n\cdot\frac{{}_{n-1}\mathrm C_{k-1}}{3^{n-1}} \quad (\because k\,{}_n\mathrm C_k = n\,{}_{n-1}\mathrm C_{k-1}) \\ &= \frac{n}{3^{n-1}}\sum_{k = 1}^{n-1}{}_{n-1}\mathrm C_{k-1} \\ &= \frac{n}{3^{n-1}}\{ (1+1)^{n-1}-{}_{n-1}\mathrm C_{n-1}\} \\ &= \frac{n(2^{n-1}-1)}{3^{n-1}} \end{aligned}$$ である. 最後から $2$ つめの等号では二項定理を使った.

(3)

最後に, $E(X_n)$ を最大にする $n$ の値を求める. $$\begin{aligned} \frac{E(X_{n+1})}{E(X_n)} &= \frac{(n+1)(2^n-1)}{3^n}\cdot\frac{3^{n-1}}{n(2^{n-1}-1)} \\ &= \frac{(2n+2)(2^n-1)}{3n(2^n-2)} \end{aligned}$$ であるから, $n \geqq 3$ のとき $$\begin{aligned} &E(X_n) > E(X_{n+1}) \iff \frac{E(X_{n+1})}{E(X_n)} < 1 \\ &\iff \frac{(2n+2)(2^n-1)}{3n(2^n-2)} < 1 \\ &\iff (2n+2)(2^n-1) < 3n(2^n-2) \\ &\iff 4n-2 < (n-2)2^n \\ &\iff \frac{4n-2}{n-2} < 2^n \iff 4+\frac{6}{n-2} < 2^n \\ &\iff n \geqq 4 \quad \left(\because 4+\frac{6}{n-2} \leqq 10\right) \end{aligned}$$ が成り立つ. また, $$E(X_2) = \frac{2}{3}, \quad E(X_3) = 1, \quad E(X_4) = \frac{28}{27}$$ である. よって, $$E(X_2) < E(X_3) < E(X_4) > E(X_5) > E(X_6) > \cdots$$ であるから, $E(X_n)$ は $n = 4$ のとき最大値 $\dfrac{28}{27}$ をとる.

　すべての玉を区別して考える.

(1)

最小で $1$ 個, 最大で $n-r+1$ 個玉を取り出せば, 赤玉が出る. $k$ 個目 $(1 \leqq k \leqq n-r+1)$ に赤玉を取り出すとき, $n-k$ 個中 $r-1$ 個の赤玉が残るから, 残った玉の組合せは ${}_{n-k}\mathrm C_{r-1}$ 通りある. これは $k$ 個目に赤玉を取り出す方法の総数に等しいから, その確率は $$\frac{{}_{n-k}\mathrm C_{r-1}}{{}_n\mathrm C_r}$$ である. ゆえに, 赤玉が出るまでに取り出す玉の個数の期待値は, $$\begin{aligned} &1\cdot\frac{{}_{n-1}\mathrm C_{r-1}}{{}_n\mathrm C_r}+\cdots +k\cdot\frac{{}_{n-k}\mathrm C_{r-1}}{{}_n\mathrm C_r}+\cdots +(n-r+1)\cdot\frac{{}_{r-1}\mathrm C_{r-1}}{{}_n\mathrm C_r} \\ &= \frac{1}{{}_n\mathrm C_r}\left(\begin{array}{ccccc} {}_{n-1}\mathrm C_{r-1}+ & \cdots & +{}_{n-k}\mathrm C_{r-1}+ & \cdots & +{}_{r-1}\mathrm C_{r-1} \\ {} & \ddots & \vdots & {} & \vdots \\ {} & {} & +{}_{n-k}\mathrm C_{r-1}+ & \cdots & +{}_{r-1}\mathrm C_{r-1} \\ {} & {} & {} & \ddots & \vdots \\ {} & {} & {} & {} & +{}_{r-1}\mathrm C_{r-1} \end{array}\right) \\ &= \frac{1}{{}_n\mathrm C_r}({}_n\mathrm C_r+\cdots +{}_{n-k+1}\mathrm C_r+\cdots +{}_r\mathrm C_r) \\ &= \frac{1}{{}_n\mathrm C_r}\cdot{}_{n+1}\mathrm C_{r+1} \\ &= \frac{(n+1)!}{(r+1)!(n-r)!}\div\frac{n!}{r!(n-r)!} \\ &= \frac{n+1}{r+1} \end{aligned}$$ である. ここで, 第 $2,$ 第 $3$ の等号では「ホッケー・スティック恒等式」 $${}_n\mathrm C_r+\cdots +{}_r\mathrm C_r = {}_{n+1}\mathrm C_{r+1} \quad (0 \leqq r < n)$$ (こちらを参照) を使った.

(2)

最小で $r$ 個, 最大で $n$ 個玉を取り出せば, すべての赤玉が出る. $k$ 個目 $(r \leqq k \leqq n)$ に最後の赤玉を取り出すとき, $k-1$ 個目までに $r-1$ 個の赤玉を取り出す. その方法は ${}_{k-1}\mathrm C_{r-1}$ 通りあるから, その確率は $$\frac{{}_{k-1}\mathrm C_{r-1}}{{}_n\mathrm C_r}$$ である. ゆえに, すべての赤玉が出るまでに取り出す玉の個数の期待値は, $$\begin{aligned} \sum_{k = r}^nk\cdot\frac{{}_{k-1}\mathrm C_{r-1}}{{}_n\mathrm C_r} &= \frac{1}{{}_n\mathrm C_r}\sum_{k = r}^nr\cdot{}_k\mathrm C_r \quad (\because k\cdot{}_{k-1}\mathrm C_{r-1} = r\cdot{}_k\mathrm C_r) \\ &= \frac{r\cdot{}_{n+1}\mathrm C_{r+1}}{{}_n\mathrm C_r} \\ &= \frac{r\cdot\dfrac{n+1}{r+1}{}_n\mathrm C_r}{{}_n\mathrm C_r} \quad (\because{}_{n+1}\mathrm C_{r+1} = \frac{n+1}{r+1}\cdot{}_n\mathrm C_r) \\ &= \frac{r(n+1)}{r+1} \end{aligned}$$ である. ここで, 第 $2$ の等号では「ホッケー・スティック恒等式」 $$\sum_{k = r}^n{}_k\mathrm C_r = {}_{n+1}\mathrm C_{r+1} \quad (0 \leqq r < n)$$ (こちらを参照) を使った.