組合せ
組合せ
定義《組合せ》
$n,$ $r$ を $n \geqq r > 0$ なる整数とする.
異なる $n$ 個のものから $r$ 個のものを選んで $1$ 組にしたものを, $n$ 個から $r$ 個を取る組合せ (combination) と呼び,
その方法の総数を ${}_n\mathrm C_r$ で表す.
$n = 0$ または $r = 0$ のときは, ${}_n\mathrm C_r = 1$ と定める.
${}_n\mathrm C_r$ の形に表された数を二項係数 (binomial coefficient) と呼ぶ.
定理《二項係数の公式》
$n \geqq r > 0$ なる整数 $n,$ $r$ に対して,
\[ {}_n\mathrm C_r = \frac{{}_n\mathrm P_r}{r!} = \frac{n!}{r!(n-r)!}\]
が成り立つ.
証明
$n$ 個から $r$ 個を取る組合せにおいて, 取り出した $r$ 個に順序をつける方法は $r!$ 通りあり,
それらを合算すると $n$ 個から $r$ 個を取る順列の総数 ${}_n\mathrm P_r$ になるから,
\[ {}_n\mathrm C_r\times r! = {}_n\mathrm P_r\]
が成り立つ.
よって, 両辺を $r!$ で割ると, 求める等式が得られる.
問題《パスカルの法則とホッケー・スティック恒等式》
$0 \leqq r < n$ なる整数 $n,$ $r$ に対して, 次のことを示せ.
- (1)
- ${}_{n+1}\mathrm C_{r+1} = {}_n\mathrm C_r+{}_n\mathrm C_{r+1}$ が成り立つ.
- (2)
- $\displaystyle\sum\limits_{k = r}^n{}_k\mathrm C_r = {}_{n+1}\mathrm C_{r+1}$ が成り立つ.
解答例
- (1)
- 二項係数の定義により, \[\begin{aligned} {}_n\mathrm C_r+{}_n\mathrm C_{r+1} &= \frac{n!}{r!(n-r)!}+\frac{n!}{(r+1)!\{ n-(r+1)\}!} \\ &= \frac{n!\{ (r+1)+(n-r)\}}{(r+1)!(n-r)!} \\ &= \frac{(n+1)!}{(r+1)!\{ (n+1)-(r+1)\}!} \\ &= {}_{n+1}\mathrm C_{r+1} \end{aligned}\] が成り立つ.
- (2)
- (1) により ${}_k\mathrm C_r = {}_{k+1}\mathrm C_{r+1}-{}_k\mathrm C_{r+1}$ $(r < k \leqq n)$ であるから, \[\begin{aligned} \sum_{k = r}^n{}_k\mathrm C_r &= {}_r\mathrm C_r+({}_{r+2}\mathrm C_{r+1}-{}_{r+1}\mathrm C_{r+1})\\ &\qquad +\cdots +({}_{n+1}\mathrm C_{r+1}-{}_n\mathrm C_{r+1}) \\ &= {}_r\mathrm C_r-{}_{r+1}\mathrm C_{r+1}+{}_{n+1}\mathrm C_{r+1} \\ &= 1-1+{}_{n+1}\mathrm C_{r+1} \\ &= {}_{n+1}\mathrm C_{r+1} \end{aligned}\] が成り立つ.
別解 1: 組合せを利用
- (1)
- 特定の人物 A を含む $n+1$ 人から $r+1$ 人を選ぶ方法を考える.
- (i)
- A を選ぶ場合. A 以外の $n$ 人から $r$ 人を選ぶ ${}_n\mathrm C_r$ 通りある.
- (ii)
- A を選ばない場合. A 以外の $n$ 人から $r+1$ 人を選ぶ ${}_n\mathrm C_{r+1}$ 通りある.
- (2)
- $n+1$ 人 A${}_1,$ $\cdots,$ A${}_n,$ A${}_{n+1}$ から $r+1$ 人を選ぶ方法の総数は, ${}_{n+1}\mathrm C_{r+1}$ である. このうち, A${}_1,$ $\cdots,$ A${}_{j-1}$ $(1 \leqq j \leqq n-r+1)$ を選ばず, A${}_j$ を選ぶ方法の総数は, A${}_{j+1},$ $\cdots,$ A${}_{n+1}$ から $r$ 人を選ぶ方法の総数に等しく, ${}_{n+1-j}\mathrm C_r$ である. これを $j$ の値を変えながら加えると, \[ {}_{n+1}\mathrm C_{r+1} = \sum_{j = 1}^{n-r+1}{}_{n+1-j}\mathrm C_r = \sum_{k = r}^n{}_k\mathrm C_r\] が得られる.
別解 2: 二項定理 (数学 II) を利用
- (1)
- \[ (1+x)^{n+1} = (1+x)^n+x(1+x)^n\] において, 左辺の展開式で $r+1$ 次の項は ${}_{n+1}\mathrm C_{r+1}x^{r+1}$ であり, 右辺の展開式で $r+1$ 次の項は \[ {}_n\mathrm C_{r+1}x^{r+1}+x\cdot {}_n\mathrm C_rx^r = ({}_n\mathrm C_r+{}_n\mathrm C_{r+1})x^{r+1}\] だから, 係数を比較すると ${}_{n+1}\mathrm C_{r+1} = {}_n\mathrm C_r+{}_n\mathrm C_{r+1}$ が得られる.
別解 3: 数学的帰納法
- (2)
- (i)
- ${}_1\mathrm C_1 = {}_2\mathrm C_2 = 1$ から, $n = 1$ のとき等式が成り立つ.
- (ii)
- $n = m$ ($m$: 正の整数) のとき等式が成り立つとすると, \[\begin{aligned} \sum_{k = r}^{m+1}{}_k\mathrm C_r &= \sum_{k = r}^m{}_k\mathrm C_r+{}_{m+1}\mathrm C_r \\ &= {}_{m+1}\mathrm C_{r+1}+{}_{m+1}\mathrm C_r \\ &= {}_{m+2}\mathrm C_{r+1} \quad (\because (1)) \end{aligned}\] となるから, $n = m+1$ のとき等式が成り立つ.
参考
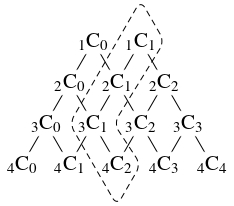
- (1) の等式 ${}_{n+1}\mathrm C_{r+1} = {}_n\mathrm C_r+{}_n\mathrm C_{r+1}$ は「パスカルの法則」(Pascal's rule) と呼ばれ, 二項係数を下図のように並べると (パスカルの三角形), 各位置の数は左上の数と右上の数の和になることを表している.
- (2) の等式については, 例えば $n = 3,$ $r = 1$ の場合の ${}_4\mathrm C_2 = {}_1\mathrm C_1+{}_2\mathrm C_1+{}_3\mathrm C_1$ の各項を破線で囲むと, 下図のようになる.
このことから, 等式 $\displaystyle\sum\limits_{k = r}^n{}_k\mathrm C_r = {}_{n+1}\mathrm C_{r+1}$ はしばしば「ホッケー・スティック恒等式」(hockey stick identity) と呼ばれる.
問題《中央二項係数の評価》
正の整数 $n$ に対して ${}_{2n}\mathrm C_n \leqq 2^{2n-1}$ が成り立つことを示せ.
また, 等号成立条件を求めよ.
解答例
$p_n = \dfrac{{}_{2n}\mathrm C_n}{2^{2n}}$ $(n \geqq 1)$ とおく.
$p_n$ が最大値 $\dfrac{1}{2}$ をとることを示せばよい.
\[\begin{aligned}
\frac{p_{n+1}}{p_n} &= \frac{{}_{2n+2}\mathrm C_{n+1}}{2^{2n+2}}\cdot\frac{2^{2n}}{{}_{2n}\mathrm C_n} = \frac{{}_{2n+2}\mathrm C_{n+1}}{{}_{2n}\mathrm C_n}\cdot\frac{2^{2n}}{2^{2n+2}} \\
&= \frac{(2n+2)!}{(n+1)!(n+1)!}\cdot\frac{n!n!}{(2n)!}\cdot\frac{1}{4} = \frac{(2n+2)(2n+1)}{(n+1)(n+1)}\cdot\frac{1}{4} \\
&= \frac{2n+1}{2n+2} < 1
\end{aligned}\]
であるから, $p_n > p_{n+1}$ が成り立つ.
よって, $p_n$ は $n = 1$ のとき最大値 $\dfrac{{}_{2}\mathrm C_1}{2^2} = \dfrac{1}{2}$ をとる.
ゆえに, ${}_{2n}\mathrm C_n \leqq 2^{2n-1}$ が成り立ち, 等号成立は $n = 1$ のときに限る.
参考
${}_{2n}\mathrm C_n$ の形の二項係数を「中央二項係数」(central binomial coefficient) と呼ぶ.
「中央二項係数」は, 数学のさまざまな問題で現れる.
問題《公平にものを分配する方法の総数》
異なる $nr$ 個のものを $n$ 人に $r$ 個ずつ配る方法の総数を求めよ.
解答例
求める場合の数は,
\[\begin{aligned}
&{}_{nr}\mathrm C_r\cdot {}_{nr-r}\mathrm C_r\cdot\cdots\cdot{}_{r}\mathrm C_r \\
&= \frac{(nr)!}{r!(nr-r)!}\cdot\frac{(nr-r)!}{r!(nr-2r)!}\cdot\cdots\cdot\frac{r!}{r!0!} \\
&= \frac{(nr)!}{(r!)^n}
\end{aligned}\]
である.
問題《多角形の対角線に関する場合の数》
$n$ を $3$ 以上の整数とする.
凸 $n$ 角形において, 次の数を求めよ.
ただし, どの $3$ 本の対角線も $1$ 点で交わらないとする.
- (1)
- 対角線の本数.
- (2)
- 対角線の交点 (頂点を除く) の個数.
- (3)
- 対角線がそれらの交点により切り取られてできる線分の本数.
解答例
- (1)
- $n$ 個の頂点から $2$ 個を選ぶと, 対角線または辺が決まる.
その場合の数は ${}_n\mathrm C_2$ であり, 辺は $n$ 本あるから, 対角線の本数は
である.${}_n\mathrm C_2\!-\!n = \dfrac{n(n\!-\!1)}{2}\!-\!n = \dfrac{n\{ (n\!-\!1)\!-\!2\}}{2} = \dfrac{n(n\!-\!3)}{2}$ (本) - (2)
- $n$ 個の頂点から $4$ 個を選ぶと, 四角形が決まり, 対角線の交点 (頂点を除く) が決まる.
よって, その個数は
である.${}_n\mathrm C_4 = \dfrac{n(n-1)(n-2)(n-3)}{4}$ (個) - (3)
- $1$ 本の対角線は, 他の対角線と
の点で交わり, それらの交点によって$\dfrac{n(n\!-\!1)(n\!-\!2)(n\!-\!3)}{4}\div\dfrac{n(n\!-\!3)}{2} = \dfrac{(n\!-\!1)(n\!-\!2)}{2}$ (個)
の線分に分けられる. よって, 求める本数は,$\dfrac{(n-1)(n-2)}{2}+1 = \dfrac{n^2-3n+4}{2}$ (本)
である.$\dfrac{n(n^2-3n+4)}{2}$ 本
参考
- 凸 $n$ 角形において, どの $3$ 本の対角線も $1$ 点で交わらないとき, 対角線により $n$ 角形が分割されてできる領域の個数は,「モーザの円の分割問題」(こちらを参照) の解から点の個数を引いた数 \[\begin{aligned} &\frac{1}{24}(n^4-6n^3+23n^2-18n+24)-n \\ &= \frac{1}{24}(n^4-6n^3+23n^2-42n+24) \end{aligned}\] である.
- 正の整数 $m$ に対して, 正の整数全体を定義域とする関数 $\delta _m(n)$ を \[\delta _m(n) = \begin{cases} 1 & (n \equiv 0 \pmod m), \\ 0 & (n \not\equiv 0 \pmod m) \end{cases}\] で定める. このとき, 正 $n$ 角形の対角線の交点の総数は \[\begin{aligned} &{}_n\mathrm C_4+\frac{-5n^3+45n^2-70n+24}{24}\cdot\delta _2(n) \\ &-\frac{3n}{2}\cdot\delta _4(n)+\frac{-45n^2+262n}{6}\cdot\delta _6(n)+42n\cdot\delta _{12}(n) \\ &+60n\cdot\delta _{18}(n)+35n\cdot\delta _{24}(n)-38n\cdot\delta _{30}(n) \\ &-82n\cdot\delta _{42}(n)-330n\cdot\delta _{60}(n)-144n\cdot\delta _{84}(n) \\ &-96n\cdot\delta _{90}(n)-144n\cdot\delta _{120}(n)-96n\cdot\delta _{210}(n) \end{aligned}\] であることが知られている (B. Poonen and M. Rubinstein, "The number of intersection points made by the diagonals of a regular polygon," SIAM J. Disc. Math., 11 (1998), no. 1, 135–156).
問題《正多角形の頂点を結ぶ三角形の個数》
$n$ を $3$ 以上の整数とする.
正 $n$ 角形 $\mathrm P_1\mathrm P_2\cdots\mathrm P_n$ の頂点を結ぶ次のような三角形の個数をそれぞれ求めよ.
- (1)
- 任意の三角形.
- (2)
- 二等辺三角形.
- (3)
- 鋭角三角形.
解答例
- (1)
- 正 $n$ 角形の $n$ 個の頂点のうち $3$ 点を選べば三角形ができるから, 求める個数は \[ {}_n\mathrm C_3 = \frac{n(n-1)(n-2)}{6}\] である.
- (2)
- (I)
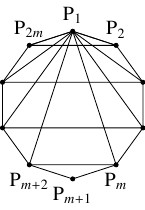
- $n = 2m$ ($m$: $2$ 以上の整数) のとき.
- (i)
- $n$ が偶数で $3$ の倍数でないとき.
正三角形は存在せず, $\mathrm P_1$ を頂点とする二等辺三角形は $m-1$ 個あるから,
二等辺三角形の個数は
\[ n(m-1) = \frac{n(n-2)}{2}\]
である.
- (ii)
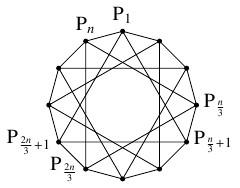
- $n$ が $6$ の倍数であるとき.
(i) の二等辺三角形の中に $3\cdot\dfrac{n}{3}$ 個の正三角形が含まれているから,
二等辺三角形の個数は, 余分に数えられている個数 $2\cdot\dfrac{n}{3}$ を引いた
\[ \frac{n(n-2)}{2}-2\cdot\frac{n}{3} = \frac{n(3n-10)}{6}\]
である.
- (II)
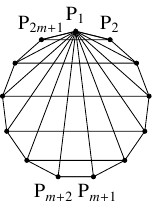
- $n = 2m+1$ ($m$: 正の整数) のとき.
- (i)
- $n$ が奇数で $3$ の倍数でないとき.
正三角形は存在せず, $\mathrm P_1$ を頂点とする二等辺三角形は $m$ 個あるから,
二等辺三角形の個数は
\[ nm = \frac{n(n-1)}{2}\]
である.
- (ii)
- $n$ が奇数で $3$ の倍数であるとき.
(i) の二等辺三角形の中に $3\cdot\dfrac{n}{3}$ 個の正三角形が含まれているから,
二等辺三角形の個数は, 余分に数えられている個数 $2\cdot\dfrac{n}{3}$ を引いた
\[ \frac{n(n-1)}{2}-2\cdot\frac{n}{3} = \frac{n(3n-7)}{6}\]
である.
- (3)
- $n$ の偶奇で場合分けして, 直角三角形, 鈍角三角形の個数を求め, それから鋭角三角形の個数を導き出す.
- (i)
- $n = 2m$ ($m$: $2$ 以上の整数) のとき.
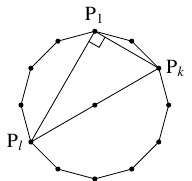
$\triangle\mathrm P_1\mathrm P_k\mathrm P_l$ $(2 \leqq k < l \leqq n)$ において $\angle\mathrm P_1 = 90^\circ$ であるためには
\[ l = k+m, \quad 2 \leqq k < l \leqq n\]
つまり
\[ 2 \leqq k \leqq m, \quad l = k+m \quad [1]\]
であることが必要十分である.
$[1]$ を満たす整数 $k,$ $l$ の個数は $m-1$ であるから, 直角三角形の個数は
\[ n(m-1) = \frac{n(n-2)}{2}\]
である.
また, $\triangle\mathrm P_1\mathrm P_k\mathrm P_l$ $(2 \leqq k < l \leqq n)$ において $\angle\mathrm P_1$ が鈍角であるためには, \[ l-k > \frac{n}{2}, \quad 2 \leqq k < l \leqq n \quad \cdots [2]\] の成り立つことが必要十分である. \[ [2] \iff 2 \leqq k < l-m \leqq m\] であり, これを満たす整数 $k,$ $l$ つまり $k,$ $l-m$ の個数は \[ {}_{m-1}\mathrm C_2 = \frac{(m-1)(m-2)}{2}\] であるから, 鈍角三角形の個数は \[\begin{aligned} n\cdot\frac{(m-1)(m-2)}{2} = \frac{n(n-2)(n-4)}{8} \end{aligned}\] である.
 ゆえに, 鋭角三角形の個数は \[\begin{aligned} &\frac{n(n\!-\!1)(n\!-\!2)}{6}\!-\!\frac{n(n\!-\!2)}{2}\!-\!\frac{n(n\!-\!2)(n\!-\!4)}{8} \\ &= \frac{n(n-2)(n-4)}{24} \end{aligned}\] である.
ゆえに, 鋭角三角形の個数は \[\begin{aligned} &\frac{n(n\!-\!1)(n\!-\!2)}{6}\!-\!\frac{n(n\!-\!2)}{2}\!-\!\frac{n(n\!-\!2)(n\!-\!4)}{8} \\ &= \frac{n(n-2)(n-4)}{24} \end{aligned}\] である.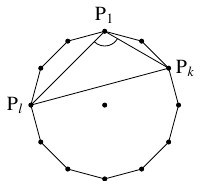
- (ii)
- $n = 2m+1$ ($m$: 正の整数) のとき. 直角三角形の個数は $0$ である. また, (i) と同様に, $\triangle\mathrm P_1\mathrm P_k\mathrm P_l$ $(2 \leqq k < l \leqq n)$ において $\angle\mathrm P_1$ が鈍角であるためには $[2]$ つまり \[ 2 \leqq k < l-m \leqq m+1\] の成り立つことが必要十分であり, これを満たす整数 $k,$ $l$ つまり $k,$ $l-m$ の個数は \[ {}_m\mathrm C_2 = \frac{m(m-1)}{2}\] であるから, 鈍角三角形の個数は \[\begin{aligned} n\cdot\frac{m(m-1)}{2} = \frac{n(n-1)(n-3)}{8} \end{aligned}\] である. ゆえに, 鋭角三角形の個数は \[\begin{aligned} &\frac{n(n-1)(n-2)}{6}-\frac{n(n-1)(n-3)}{8} \\ &= \frac{(n+1)n(n-1)}{24} \end{aligned}\] である.
カタラン数
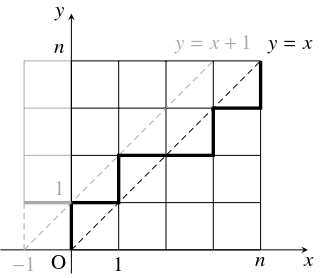
問題《カタラン数の公式》
- (1)
- $xy$ 平面の原点を出発して,
$x$ 軸方向に $1$ だけ進む, $y$ 軸方向に $1$ だけ進むのいずれかを繰り返して,
点 $(n,n)$ に至る経路において, $y \leqq x$ の部分のみを通るような場合の数 $C_n$ を求めたい.
ここで, $y > x$ の部分を通るような経路は,
初めて直線 $y = x+1$ と点を共有するまでの部分を直線 $y = x+1$ に関して折り返すことで,
点 $(-1,1)$ から点 $(n,n)$ に至る経路に対応づけることができる.
このことを使って, \[ C_n = \frac{{}_{2n}\mathrm C_n}{n+1}\] を示せ.
- (2)
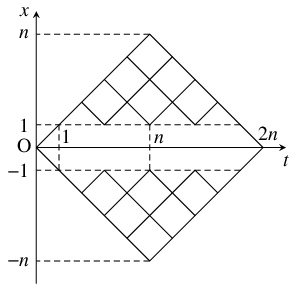
- 数直線上の動点 $\mathrm P$ は, 原点 $\mathrm O$ を出発して, コインを投げて表が出る度に正の方向に $1$ だけ移動し, 裏が出る度に負の方向に $1$ だけ移動する. 横軸をコインを投げた回数 $t$ とした $\mathrm P$ の座標 $x$ の折れ線グラフを考えることによって, $n \geqq 2$ のとき, $2n$ 回コインを投げた時点で $\mathrm P$ が $\mathrm O$ に初めて戻る場合の数は $\dfrac{2\cdot{}_{2n-2}\mathrm C_{n-1}}{n}$ であることを示せ.
(参考: $2008$ 九州大)
解答例
- (1)
- 点 $(n,n)$ への移動は, $x$ 軸方向に $1$ だけ進むことを表す矢印 $\to$ と $y$ 軸方向に $1$ だけ進むことを表す矢印 $\uparrow$ の順列で表される. よって, $y > x$ の部分を通っても通らなくてもよいとしたときの経路の総数は ${}_{2n}\mathrm C_n$ で, $y > x$ の部分を通るような経路の総数は ${}_{2n}\mathrm C_{n+1}$ であるから, \[\begin{aligned} C_n &= {}_{2n}\mathrm C_n-{}_{2n}\mathrm C_{n+1} \\ &= \frac{(2n)!}{n!n!}-\frac{(2n)!}{(n+1)!(n-1)!} \\ &= \frac{(2n)!}{n!n!(n+1)}(n+1-n) \\ &= \frac{{}_{2n}\mathrm C_n}{n+1} \end{aligned}\] である.
- (2)
- $1$ 回目に表が出て $t = 2n$ のときに初めて $x = 0$ となるとき,
動点 $\mathrm P$ の座標 $x$ の折れ線グラフは, $(0,0),$ $(1,1)$ を結ぶ線分, $(2n-1,1),$ $(2n,0)$ を結ぶ線分と,
$2n-2$ 本の直線 $x = t-2k$ $(0 \leqq k \leqq n-2),$ $x = -t+2l$ $(2 \leqq l \leqq n)$ が走る碁盤目の $x \geqq 1$ の部分からなる.
その総数は (1) の結果により \[ C_{n-1} = \frac{{}_{2n-2}\mathrm C_{n-1}}{n}\] であるから, 対称性により, 求める場合の数は \[ 2C_{n-1} = \frac{2\cdot{}_{2n-2}\mathrm C_{n-1}}{n}\] である.
参考
- (1) の場合の数は「カタラン数」(Catalan number) と呼ばれる.
- (2) の動点 $\mathrm P$ のように, 次に移動する位置が確率的に無作為に決まる運動を「ランダム・ウォーク」(random walk) と呼ぶ. コインを $2n$ 回投げ終えるまでに $\mathrm P$ が原点に戻る確率については, こちらを参照されたい.
問題《カタラン数のなす数列の漸化式》
$xy$ 平面の原点を出発して,
$x$ 軸方向に $1$ だけ進む, $y$ 軸方向に $1$ だけ進むのいずれかを繰り返して,
点 $(n,n)$ に至る経路において, $y > x$ の部分を通らないような場合の数を $C_n$ とおく (こちらを参照).
また, $C_0 = 1$ と定める.
ゴール前で最後に直線 $y = x$ を通過する点に着目することで,
\[ C_{n+1} = \sum_{k = 0}^nC_kC_{n-k}\]
が成り立つことを示せ.
解答例
$y > x$ の部分を通らないという条件のもとで,
原点から点 $(n+1,n+1)$ に至る経路において, ゴール前で最後に直線 $y = x$ を通過する点が $(k,k)$ $(0 \leqq k \leqq n)$ であるような経路は,
必ず $3$ 点 $(k,k),$ $(k+1,k),$ $(n+1,n)$ を経由する.
原点から点 $(k,k)$ に至る経路は $C_k$ 通り, 点 $(k,k)$ から点 $(k+1,k)$ に至る経路は $1$ 通り, 点 $(k+1,k)$ から点 $(n+1,n)$ に至る経路は $C_{n-k}$ 通り, 点 $(n+1,n)$ から点 $(n+1,n+1)$ に至る経路は $1$ 通りあるから, その場合の数は
\[ C_k\cdot 1\cdot C_{n-k}\cdot 1 = C_kC_{n-k}\]
である.
よって,
\[ C_{n+1} = \sum_{k = 0}^nC_kC_{n-k}\]
が成り立つ.
問題《素数であるカタラン数》
各正の整数 $n$ に対して
\[ C_n = \frac{{}_{2n}\mathrm C_n}{n+1}\]
で定まる整数 $C_n$ を「カタラン数」と呼ぶ (こちらを参照).
- (1)
- \[ C_{n+1} = \dfrac{2(2n+1)}{n+2}C_n \quad \cdots [1]\] が成り立つことを示せ.
- (2)
- $n \geqq 4$ のとき, \[ C_n > n+2 \quad \cdots [2]\] が成り立つことを示せ.
- (3)
- 素数である「カタラン数」をすべて求めよ.
(参考: $2021$ 東京工業大)
解答例
- (1)
- 二項係数の定義により, \[\begin{aligned} C_{n+1} &= \frac{{}_{2n+2}\mathrm C_{n+1}}{n+2} \\ &= \frac{(2n+2)!}{(n+2)\cdot (n+1)!(n+1)!} \\ &= \frac{(2n+2)(2n+1)}{(n+2)(n+1)}\cdot\frac{(2n)!}{(n+1)\cdot n!n!} \\ &= \frac{2(2n+1)}{n+2}C_n \quad \cdots [1] \end{aligned}\] が成り立つ.
- (2)
- (i)
- $n = 4$ のとき. \[ C_4 = \frac{{}_8\mathrm C_4}{5} = 14 > 6 = 4+2\] であるから, $[2]$ が成り立つ.
- (ii)
- $n = k$ $(k \geqq 4)$ のとき $[2]$ が成り立つとする. このとき, \[\begin{aligned} C_{k+1} &= \frac{2(2k+1)}{k+2}C_k \quad (\because [1]) \\ &> \frac{2(2k+1)}{k+2}(k+2) = 2(2k+1) \\ &> (k+1)+2 \quad (\because k \geqq 4 \Longrightarrow 3k > 1) \end{aligned}\] となり, $n = k+1$ のとき $[2]$ が成り立つ.
- (3)
- $C_1 = 1$ は素数でない.
- $C_2 = 2,$ $C_3 = 5$ は素数である.
- $n \geqq 4$ のとき. $[1]$ において $C_{n+1}$ は整数であるから, $2(2n+1)C_n$ は $n+2$ で割り切れる. $n \geqq 4$ により $2$ は $n+2$ で割り切れない. \[ 2n+1 = 2(n+2)-3\] であり, $n \geqq 4$ により $3$ は $n+2$ で割り切れないから, $2n+1$ は $n+2$ で割り切れない. よって, $C_n$ は $n+2$ で割り切れる. さらに, $[2]$ により, $C_n$ を $n+2$ で割った商は $1$ より大きい. したがって, $C_n$ は合成数である.
問題《奇数であるカタラン数》
整数 $C_0,$ $C_1,$ $\cdots,$ $C_n,$ $\cdots$ を順次
\[ C_0 = 1, \quad C_{n+1} = \sum_{k = 0}^nC_kC_{n-k}\]
で定める (こちらを参照).
以下, $n$ を正の整数とし, $C_n$ が奇数であるとする.
$n$ を $2$ で割った商を $q,$ 余りを $r$ とおく.
- (1)
- $r = 1$ であり, $C_q$ も奇数であることを示せ.
- (2)
- $n$ はある正の整数 $d$ を用いて $n = 2^d-1$ と表されることを示せ.
解答例
- (1)
- \[ C_n = \begin{cases} 2(C_0C_{2q-1}+\cdots +C_{q-1}C_q)& (r = 0), \\ 2(C_0C_{2q}+\cdots +C_{q-1}C_{q+1})+C_q{}^2 & (r = 1) \\ \end{cases}\] であるから, $C_n$ が奇数であるとき, $r = 1$ であり, $C_q{}^2$ は奇数, したがって $C_q$ は奇数である.
- (2)
- $n$ を二進法で \[ n = a_{d-1}\cdot 2^{d-1}+\cdots +a_1\cdot 2+a_0 \quad (a_k = 0,1) \] と表す. $C_n$ が奇数であるという仮定と (1) の結果により, $a_0 = 1$ が得られる. また, $n$ を $2$ で割った商 \[ q = a_{d-1}\cdot 2^{d-2}+\cdots +a_1\] についても, $C_q$ が奇数であることから, 同様に $a_1 = 1$ が得られる. この操作を続けると, \[ a_0 = a_1 = \cdots = a_{d-1} = 1\] となる (ちなみに, $C_0 = 1$ が奇数であることは自明である). ゆえに, $n$ は \[ n = 2^{d-1}+\cdots +2+1 = 2^d-1\] と表される.
参考
「カタラン数」$C_0,$ $C_1,$ $\cdots,$ $C_n,$ $\cdots$ は
\[ C_0 = 1, \quad C_{n+1} = \sum_{k = 0}^nC_kC_{n-k}\]
で定まる.
正の整数 $d$ を用いて $2^d-1$ の形に表される正の整数は「メルセンヌ数」(Mersenne number) と呼ばれる.
本問で示したのは, 奇数である「カタラン数」は「メルセンヌ数」番目の「カタラン数」に限るということである.
