順列・円順列
順列
問題《順列の漸化式》
$0 \leqq r < n$ なる整数 $n,$ $r$ に対して,
\[ {}_{n+1}\mathrm P_{r+1} = (r+1){}_n\mathrm P_r+{}_n\mathrm P_{r+1}\]
が成り立つことを示せ.
解答例
順列の定義により,
\[\begin{aligned}
&(r+1){}_n\mathrm P_r+{}_n\mathrm P_{r+1} = (r+1)\frac{n!}{(n-r)!}+\frac{n!}{(n-r-1)!} \\
&= (r+1+n-r)\frac{n!}{(n-r)!} = \frac{(n+1)!}{(n-r)!} \\
&= \frac{(n+1)!}{(n+1-r-1)!} = {}_{n+1}\mathrm P_{r+1}
\end{aligned}\]
が成り立つ.
別解
$n+1$ 人のうち $r+1$ 人を並べる順列を考える.
$n+1$ 人の中に含まれる特定の人物 A を選ぶか選ばないかで場合に分けて数える.
- (i)
- A を選ぶ場合. A が何番目に並ぶかを決めた後, 残りの $n$ 人のうち $r$ 人を他の場所に並べる $(r+1){}_n\mathrm P_r$ 通りの並べ方がある.
- (ii)
- A を選ばない場合. 残りの $n$ 人のうち $r+1$ 人を並べる ${}_n\mathrm P_{r+1}$ 通りの並べ方がある.
問題《モンモール数の関係式》
$1,$ $\cdots,$ $n$ の順列において, $1 \leqq i \leqq n$ なる各整数 $i$ に対して $i$ 番目に $i$ が並ばないような順列の総数を $a_n$ で表す.
また, $a_0 = 1$ と定める.
このとき,
\[ n! = \sum_{k = 0}^n{}_n\mathrm C_k\,a_{n-k}\]
が成り立つことを示せ.
解答例
$0 \leqq k \leqq n$ なる各整数 $k$ に対して, $1,$ $\cdots,$ $n$ から $k$ 個の数を選ぶ方法は ${}_n\mathrm C_k$ 通りあり, その各々に対してそれ以外の $n-k$ 個の数をもとと異なる位置に並べ替える方法は $a_{n-k}$ 通りあるので, ちょうど $k$ 個の数を固定する順列は ${}_n\mathrm C_k\,a_{n-k}$ 個ある.
よって,
\[ n! = \sum_{k = 0}^n{}_n\mathrm C_k\,a_{n-k}\]
が成り立つ.
参考
- それぞれをもとの位置と異なる位置に並べ替える順列は「完全順列」または「攪乱順列」(derangement) と呼ばれる. $n$ 個のものの「完全順列」の総数は「モンモール数」(Montmort number) と呼ばれる.
- 一般に, 数列 $\{ a_n\},$ $\{ b_n\}$ について, \[ b_n = \sum_{k = 0}^n{}_n\mathrm C_k\,a_{n-k} \Longrightarrow a_n = \sum_{k = 0}^n(-1)^k{}_n\mathrm C_k\,b_{n-k}\] が成り立つという「反転公式」が知られている (参考: 山本幸一,『順列・組合せと確率』, 岩波書店, p.91). よって, 本問の結果により, \[ a_n = \sum_{k = 0}^n(-1)^k{}_n\mathrm C_k\,(n-k)! = n!\sum_{k = 0}^n\frac{(-1)^k}{k!}\] が成り立つ. この公式については, こちらとこちらも参照.
- 「モンモール数」$a_n$ を求めるには, $2$ 項間漸化式 \[ a_{n+1} = (n+1)a_n+(-1)^{n+1}\] を利用するのが便利である (上記の公式から得られる).
- 初めの方の「モンモール数」$a_n$ を求めると, 次の表のようになる.
$n$ $1$ $2$ $3$ $4$ $5$ $6$ $7$ $8$ $9$ $10$ $a_n$ $0$ $1$ $2$ $9$ $44$ $265$ $1854$ $14833$ $133496$ $1334961$
問題《第 $1$ 種オイラー数》
$n,$ $r$ を $n \geqq r$ なる正の整数とする.
$1,$ $\cdots,$ $n$ の順列 $n!$ 個のうち, 前後の関係が昇順であるような $2$ 数 (位置的に隣り合う) がちょうど $r$ 組あるような順列の総数を $E(n,r)$ で表す.
このとき,
- (A)
- $E(n,r) = E(n,n-1-r)$
- (B)
- $E(n+1,r+1) = (n-r)E(n,r)+(r+2)E(n,r+1)$
解答例
- (A)
- $1,$ $\cdots,$ $n$ の順列 $n!$ 個のうち, 前後の関係が昇順であるような $2$ 数がちょうど $r$ 組あるような順列において, 前後の関係が降順であるような $2$ 数は $n-1-r$ 組ある. \[ a_k = n-k+1 \quad (1 \leqq k \leqq n)\] として, $a_1,$ $\cdots,$ $a_n$ の順列 $n!$ 個のうち, 前後の関係が昇順であるような $2$ 数がちょうど $n-r-1$ 組あるような順列の総数は添え字に着目すると $E(n,n-1-r)$ 個あることがわかるから, \[ E(n,r) = E(n,n-1-r)\] が成り立つ.
- (B)
- $1,$ $\cdots,$ $n$ の順列の先頭, 隙間, 末尾のいずれかに $n+1$ を入れて, 前後の関係が昇順であるような $2$ 数がちょうど $r+1$ 組あるような順列を作る.
- (i)
- $1,$ $\cdots,$ $n$ の順列において, 前後の関係が昇順であるような $2$ 数がちょうど $r$ 組あるとき.
前後の関係が昇順であるような $2$ 数の組を $1$ 組増やすには,
降順であるような $2$ 数の隙間 $n-1-r$ 箇所か,
末尾のどこかに $n+1$ を入れればよい.
この場合の数は,
$E(n,r)\{ (n-1-r)+1\} = (n-r)E(n,r)$ 通り. - (ii)
- $1,$ $\cdots,$ $n$ の順列において, 前後の関係が昇順であるような $2$ 数がちょうど $r+1$ 組あるとき.
前後の関係が昇順であるような $2$ 数の組を増やさないには,
昇順であるような $2$ 数の隙間 $r+1$ 箇所か,
先頭のどこかに $n+1$ を入れればよい.
この場合の数は,
$E(n,r+1)\{ (r+1)+1\} = (r+2)E(n,r+1)$ 通り.
参考
- $1,$ $\cdots,$ $n$ の順列 $n!$ 個のうち, 前後の関係が昇順であるような $2$ 数 (位置的に隣り合う) がちょうど $r$ 組あるような順列の総数を「第 $1$ 種オイラー数」(Eulerian number of the first kind) と呼ぶ. 世界的には $\left\langle\begin{matrix} n \\ r \end{matrix}\right\rangle$ という記号で表すことが多い. 初めの方の「第 $1$ 種オイラー数」を求めると, 次の表のようになる.
| $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | |
| $1$ | $1$ | |||||||||
| $2$ | $1$ | $1$ | ||||||||
| $3$ | $1$ | $4$ | $1$ | |||||||
| $4$ | $1$ | $11$ | $11$ | $1$ | ||||||
| $5$ | $1$ | $26$ | $66$ | $26$ | $1$ | |||||
| $6$ | $1$ | $57$ | $302$ | $302$ | $57$ | $1$ | ||||
| $7$ | $1$ | $120$ | $1191$ | $2416$ | $1191$ | $120$ | $1$ | |||
| $8$ | $1$ | $247$ | $4293$ | $15619$ | $15619$ | $4293$ | $247$ | $1$ | ||
| $9$ | $1$ | $502$ | $14608$ | $88234$ | $156190$ | $88234$ | $14608$ | $502$ | $1$ | |
| $10$ | $1$ | $1013$ | $47840$ | $455192$ | $1310354$ | $1310354$ | $455192$ | $47840$ | $1013$ | $1$ |
円順列
問題《正多面体の塗り分け》
$p$ 色を使って, 正 $p$ 面体の各面に互いに異なる色を塗る.
- (1)
- 次の各場合に, 色の塗り方は何通りあるか.
正 $p$ 面体の面の数 $p,$ $1$ つの頂点で交わる辺の本数 $q,$ 頂点の個数 $v$ を用いて表せ.
- (i)
- 全頂点を固定する場合.
- (ii)
- $1$ つの頂点を固定する場合.
- (iii)
- どの頂点も固定しない場合.
- (2)
- $p = 4,$ $6,$ $8,$ $12,$ $20$ の各場合に, 色の塗り方の総数を求めよ.
解答例
- (1)
-
- (i)
- 全頂点を固定する場合. 色の塗り方は $p$ 個から $p$ 個をとる順列の総数に等しく, $p!$ 通り.
- (ii)
- $1$ つの頂点 $\mathrm A$ を固定する場合.
$\mathrm A$ と正 $p$ 面体の中心を通る直線のまわりの回転移動で (i) の色の塗り方が $q$ 通りずつ同一視されるから, $\dfrac{p!}{q}$ 通り.
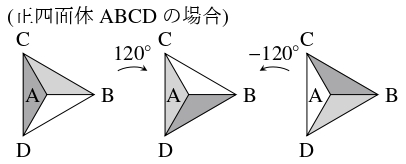
- (iii)
- どの頂点も固定しない場合. 任意の頂点を頂点 $\mathrm A$ の位置に移す移動で (ii) の色の塗り方が $v$ 通りずつ同一視されるから, $\dfrac{p!}{qv}$ 通り.
- (2)
- 正 $p$ 面体の $1$ つの頂点で交わる辺の本数 $q,$ 頂点の個数 $v$ は, 次の通りである.
よって, (1) の (iii) の結果から, 求める場合の数はそれぞれ \[\begin{aligned} \frac{4!}{3\cdot 4} &= 2, \\ \frac{6!}{3\cdot 8} &= 30, \\ \frac{8!}{4\cdot 6} &= 1\,680, \\ \frac{12!}{3\cdot 20} &= 7\,983\,360, \\ \frac{20!}{5\cdot 12} &= 40\,548\,366\,802\,944\,000 \end{aligned}\] である.
$p$ $q$ $v$ $4$ $3$ $4$ $6$ $3$ $8$ $8$ $4$ $6$ $12$ $3$ $20$ $20$ $5$ $12$
参考
平面, 球面上の地図は, 隣り合う領域に互いに異なる色を塗るとき, $4$ 色で塗り分けられることが,「四色定理」として知られている.
球面への投影を考えると, すべての凸多面体は $4$ 色で塗り分けられることがわかる.
塗り分けに必要な色の数の最小値は, 正四面体では $4,$ 正六面体では $3,$ 正八面体では $2,$ 正十二面体では $4,$ 正二十面体では $3$ である.
