本格数学クイズ (組合せ論)
確率に関する問題でも, 組合せ論的な意味合いが強い問題はこちらに掲載しています.
場合の数
クイズ《試合数》
総当たりのリーグ戦の試合数, トーナメント戦で優勝チームを決めるのに必要な試合数を比較するとき, 前者が後者を上回るのは, 参加チームが何チーム以上のときか.
(有名問題)
答え
$3$ チーム以上.
解説
$n$ を $2$ 以上の整数とする.
- (1)
- $n$ チームが総当たりのリーグ戦を行うときの試合数を求める. 各チームの試合数は $n-1$ である. のべ $n(n-1)$ チームが出場するが, 各試合で $2$ チームが出場するから, 試合数は全部で $\dfrac{n(n-1)}{2}$ である.
- (2)
- $n$ チームがトーナメント戦で優勝チームを決めるのに必要な試合数を求める. トーナメント戦では, $1$ 試合ごとにちょうど $1$ チームの敗者が決まり, 最後に $1$ 度も負けなかった $1$ チームが優勝するから, 必要な試合数は $n-1$ である.
- (3)
- (1), (2) の試合数を比較する. \[\frac{n(n-1)}{2}-(n-1) = \frac{(n-1)(n-2)}{2}\] から \[\frac{n(n-1)}{2} > n-1 \iff n < 1,\ 2 < n\] であり, $n$ は $2$ 以上の整数であるから, (1) の試合数が (2) の試合数を上回るのは \[ n \geqq 3\] のときである.
クイズ《パスワードの作り方》
$2n$ 個の文字を各文字の候補として $n$ 文字のパスワードを作る.
重複する文字がある確率が重複する文字がない確率より高くなるのは, パスワードが何文字のときか.
(オリジナル)
答え
$4$ 文字以上.
解説
$2n$ 個の文字を各文字の候補として $n$ 文字のパスワードを作るとき, 重複する文字がない確率は
\[\frac{{}_{2n}\mathrm P_n}{(2n)^n} = \frac{(2n)\cdots (n+1)}{(2n)^n}\]
である.
これが $\dfrac{1}{2}$ より小さいとき, 重複する文字がある確率が重複する文字がない確率より高くなる.
よって,
\[\frac{(2n)\cdots (n+1)}{(2n)^n} < \frac{1}{2}\]
つまり
\[ (2n)\cdots (n+1) < 2^{n-1}n^n \quad \cdots [1]\]
を満たす正の整数 $n$ を求めればよい.
\[\begin{aligned}
&2 > 2^0\cdot 1^1, \quad 4\cdot 3 > 2^1\cdot 2^2, \quad 6\cdot 5\cdot 4 > 2^2\cdot 3^3, \\
&8\cdot 7\cdot 6\cdot 5 < 2^3\cdot 4^4
\end{aligned}\]
であるから, この不等式を満たす最小の正の整数は $n = 4$ である.
さらに, 与えられた $4$ 以上の整数 $n$ に対して $[\ast ]$ が成り立つとすると,
\[ \frac{2n+1}{n+1} = 2-\frac{1}{n+1} < \left( 1+\frac{1}{n}\right)^n = \frac{(n+1)^n}{n^n} \quad \cdots [2]\]
(二項定理により $\left( 1+\dfrac{1}{n}\right)^n > 1+n\cdot\dfrac{1}{n} = 2$) から
\[\begin{aligned}
&(2n+2)(2n+1)(2n)\cdots (n+2)(n+1) \\
&< (2n+2)(2n+1)2^{n-1}n^n \quad (\because [1]\times (2n+2)(2n+1)) \\
&= (n+1)2^n(2n+1)n^n \\
&< (n+1)2^n(n+1)^{n+1} \quad (\because [2])
\end{aligned}\]
よって
\[ (2n+2)\cdots (n+2) < 2^n(n+1)^{n+1}\]
となる.
ゆえに, $n \geqq 4$ のとき $[\ast ]$ が成り立つ.
クイズ《正多面体の塗り分け》
$p = 4,$ $6,$ $8,$ $12,$ $20$ とする.
$p$ 色を使って正 $p$ 面体の各面に互いに異なる色を塗る方法はそれぞれ何通りあるか.
(有名問題)
答え
| $p = 4$ のとき | $2$ 通り, |
| $p = 6$ のとき | $30$ 通り, |
| $p = 8$ のとき | $1\,680$ 通り, |
| $p = 12$ のとき | $7\,983\,360$ 通り, |
| $p = 20$ のとき | $40\,548\,366\,802\,944\,000$ 通り. |
解説
正 $p$ 面体において, $1$ つの頂点で交わる辺の本数を $q,$ 頂点の個数を $v$ とおく.
次の各場合に, $p$ 色を使って正 $p$ 面体の各面に互いに異なる色を塗る方法の総数を, $p,$ $q,$ $v$ を用いて表す.
ゆえに, (iii) の結果から, 求める場合の数はそれぞれ
\[\begin{aligned}
\frac{4!}{3\cdot 4} &= 2, \\
\frac{6!}{3\cdot 8} &= 30, \\
\frac{8!}{4\cdot 6} &= 1\,680, \\
\frac{12!}{3\cdot 20} &= 7\,983\,360, \\
\frac{20!}{5\cdot 12} &= 40\,548\,366\,802\,944\,000
\end{aligned}\]
である.
- (i)
- 全頂点を固定する場合.
色の塗り方は $p$ 個から $p$ 個をとる順列の総数に等しく,
$p!$ 通り. - (ii)
- $1$ つの頂点 $\mathrm A$ を固定する場合.
$\mathrm A$ と正 $p$ 面体の中心を通る直線のまわりの回転移動で (i) の色の塗り方が $q$ 通りずつ同一視されるから,
$\dfrac{p!}{q}$ 通り. 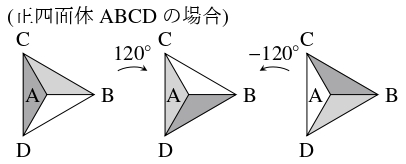
- (iii)
- どの頂点も固定しない場合.
任意の頂点を頂点 $\mathrm A$ の位置に移す移動で (ii) の色の塗り方が $v$ 通りずつ同一視されるから,
$\dfrac{p!}{qv}$ 通り.
| $p$ | $q$ | $v$ |
| $4$ | $3$ | $4$ |
| $6$ | $3$ | $8$ |
| $8$ | $4$ | $6$ |
| $12$ | $3$ | $20$ |
| $20$ | $5$ | $12$ |
参考
平面, 球面上の地図は, 隣り合う領域に互いに異なる色を塗るとき, $4$ 色で塗り分けられることが,「四色定理」として知られている.
球面への投影を考えると, すべての凸多面体は $4$ 色で塗り分けられることがわかる.
塗り分けに必要な色の数の最小値は, 正四面体では $4,$ 正六面体では $3,$ 正八面体では $2,$ 正十二面体では $4,$ 正二十面体では $3$ である.
クイズ《$6$ 本の棒を辺とする四面体の総数》
長さの異なる $6$ 本の棒があり, どの $3$ 本を選んでもそれらを辺とする三角形が作れるとする.
このとき, これらの棒を辺とする四面体は何通り作れるか.
ただし, $2$ つの四面体は, 平行移動や回転移動によって重なるとき同じ四面体とみなすが, 互いに鏡像の関係にあるとき異なる四面体とみなすものとする.
(参考: H・ステインハウス,『数学 100 の問題』,問題 37)
答え
$60$ 通り.
解説
位置が異なる四面体を異なる四面体とみなすとすると, 四面体の作り方は辺の選び方から $6!$ 通りある.
これらのうち平行移動や回転移動によって重なるものを同じ四面体とみなすとすると,
どの面を下に置くかで $4$ 通りの四面体が同じとみなされ,
底面が合同であればどの辺を手前に置くかで $3$ 通りの四面体が同じとみなされるから,
四面体の作り方は全部で
ある.
| $6!\div (4\cdot 3) = 60$ (通り) |
クイズ《公平にものを分配する方法》
異なる $nr$ 個のものを $n$ 人に $r$ 個ずつ配る方法は何通りあるか.
(有名問題)
答え
$\dfrac{(nr)!}{(r!)^n}$ 通り.
解説
求める場合の数は,
\[\begin{aligned}
&{}_{nr}\mathrm C_r\cdot {}_{nr-r}\mathrm C_r\cdot\cdots\cdot{}_{r}\mathrm C_r \\
&= \frac{(nr)!}{r!(nr-r)!}\cdot\frac{(nr-r)!}{r!(nr-2r)!}\cdot\cdots\cdot\frac{r!}{r!0!} \\
&= \frac{(nr)!}{(r!)^n}
\end{aligned}\]
である.
クイズ《偶数個のものを選ぶ方法》
異なる $n$ 個のものから偶数個 ($2$ 個以上) のものを選ぶ方法は全部で何通りあるか.
(有名問題)
答え
$2^{n-1}-1$ 通り.
解説
異なる $n$ 個のものから偶数個 ($2$ 個以上) のものを選ぶ方法は,
ある (末項は $n$ が偶数のとき ${}_n\mathrm C_n,$ $n$ が奇数のとき ${}_n\mathrm C_{n-1}$).
ここで, 二項定理により
\[ (1+x)^n = \sum_{k = 0}^n{}_n\mathrm C_kx^k\]
が成り立つから, $x = \pm 1$ を代入すると
\[\sum_{k = 0}^n{}_n\mathrm C_k = 2^n, \quad \sum_{k = 0}^n(-1)^k{}_n\mathrm C_k = 0\]
が得られる.
辺々を加えて $2$ で割ると
\[ 1+{}_n\mathrm C_2+{}_n\mathrm C_4+\cdots = 2^{n-1}\]
となるから, 求める場合の数は
| ${}_n\mathrm C_2+{}_n\mathrm C_4+\cdots$ 通り |
| $2^{n-1}-1$ 通り. |
クイズ《リーグ戦で全チームの勝敗の数が異なる確率》
$n$ チームが参加する総当たりのリーグ戦において, 全チームの勝敗の数が異なる確率はいくらか.
ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする.
(オリジナル)
答え
$\dfrac{n!}{2^{\frac{n(n-1)}{2}}}.$
解説
- (1)
- $n$ チームが参加する総当たりのリーグ戦において, 全チームの勝敗の数が異なる場合の数は, $n$ チームを $1$ 位 ($n-1$ 勝 $0$ 敗) から最下位 ($0$ 勝 $n-1$ 敗) まで順位順に並べる方法の総数に等しく,
$n!$ 通り. - (2)
- 試合数は $\dfrac{n(n-1)}{2}$ であるから, 星取表の書き方は
$2^{\frac{n(n-1)}{2}}$ 通り. - (3)
- ゆえに, 求める確率は, \[\frac{n!}{2^{\frac{n(n-1)}{2}}}\] である.
参考
実力が互角の $n$ チームが参加する総当たりのリーグ戦 (各試合で引き分けなし) で全チームの勝敗の数が異なる確率 $p_n$ は, $2 \leqq n \leqq 5$ のとき
\[\begin{aligned}
p_2 &= 1, \\
p_3 &= \frac{3}{4} = 0.75, \\
p_4 &= \frac{3}{8} = 0.375, \\
p_5 &= \frac{15}{128} = 0.1171875
\end{aligned}\]
である.
クイズ《リーグ戦で全チームが引き分ける確率》
$2n+1$ チーム $(n \geqq 1)$ が参加する総当たりのリーグ戦において, 全チームが $n$ 勝 $n$ 敗で引き分ける確率はいくらか.
ただし, 全チームの実力は互角であり, 各試合で引き分けはないものとする.
(オリジナル)
答え
$\dfrac{{}_{2n}\mathrm C_n\cdots{}_{n+k}\mathrm C_k\cdots{}_{n+1}\mathrm C_1}{2^{n(2n+1)}}.$
解説
- (1)
- 全チームが $n$ 勝 $n$ 敗で引き分ける星取表の書き方の総数を求める.
- まず, $1$ チーム ($\mathrm T_0$ と呼ぶ) の星取と, 残りのチームの $\mathrm T_0$ との試合の星取のみを書くとき, その場合の数は ${}_{2n}\mathrm C_n$ 通り.
- このとき, ちょうど $n-1$ チームが $1$ 勝 $0$ 敗になる. そのうちの $1$ チーム ($\mathrm T_1$ と呼ぶ) の星取と, 残りのチームの $\mathrm T_1$ との試合の星取のみを書き加えるとき, それは $\mathrm T_1$ の行の空欄 $2n-1$ 箇所のうち $n-1$ 箇所に白星を記すことで決まるから, その場合の数は ${}_{2n-1}\mathrm C_{n-1}$ 通り.
- これを続けていき, $r$ チーム $(1 \leqq r \leqq n)$ の空欄が埋まったとき, ちょうど $n-r+1$ チームが $r$ 勝 $0$ 敗になる (実際, 表を並べ替えると次のようになり, 右端の $(2n+1)-r-n = n-r+1$ 列には黒星のみが並ぶから, 表の対称性により下端の $n-r+1$ 行には白星のみが並ぶ).
そのうちの $1$ チーム ($\mathrm T_r$ と呼ぶ) の星取と, 残りのチームの $\mathrm T_r$ との試合の星取のみを書き加えるとき (表の配列は元に戻しておく), それは $\mathrm T_r$ の行の空欄 $2n-r$ 箇所のうち $n-r$ 箇所に白星を記すことで決まるから, その場合の数は ${}_{2n-r}\mathrm C_{n-r}$ 通り.
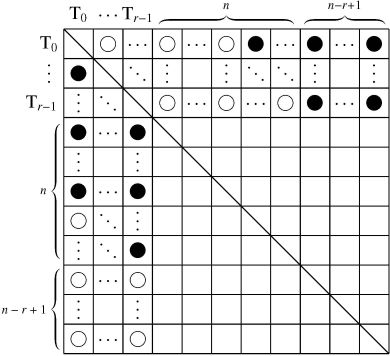
- (2)
- $2n+1$ チームが参加する総当たりのリーグ戦において, 試合数は $\dfrac{(2n+1)\cdot 2n}{2} = n(2n+1)$ であるから, 星取表の書き方は \[ 2^{n(2n+1)} \quad \cdots [2]\] 通りある.
- (3)
- $[1]\div [2]$ から, 求める確率は \[\frac{{}_{2n}\mathrm C_n\cdots{}_{n+k}\mathrm C_k\cdots{}_{n+1}\mathrm C_1}{2^{n(2n+1)}}\] である.
参考
実力が互角の $2n+1$ チームが参加する総当たりのリーグ戦 (各試合で引き分けなし) で全チームが $n$ 勝 $n$ 敗で引き分ける確率 $q_{2n+1}$ は, $1 \leqq n \leqq 5$ のとき
\[\begin{aligned}
q_3 &= \frac{1}{4} = 0.25, \\
q_5 &= \frac{9}{512} = 0.0175\cdots, \\
q_7 &= \frac{25}{65536} = 0.000381\cdots, \\
q_9 &= \frac{91875}{34359738368} = 0.00000267\cdots, \\
q_{11} &= \frac{1750329}{281474976710656} = 0.00000000621\cdots
\end{aligned}\]
である.
クイズ《完全順列の割合》
$n$ 人 $(n \geqq 2)$ の席替えで全員の席が替わる確率 $p_n$ の最大値, 最小値はいくらか (高校生向け).
また, $n$ が大きくなるにつれて $p_n$ はどのような値に近づいていくか (大学生向け).
(有名問題)
答え
最大値は $\dfrac{1}{2},$ 最小値は $\dfrac{1}{3},$ 近づいていく値は $\dfrac{1}{e}$ ($e$: ネイピア数).
解説
- (1)
- まず, $n$ 人の席替えで全員の席が替わる場合の数 $a_n$ について, 数列 $\{ a_n\}$ の漸化式を導く.
便宜的に $a_1 = 0$ と定め, $n \geqq 3$ とする.
特定の人物 A, 残った $n-1$ 人の順に行っても, 場合の数は変わらない.
A が移動する方法は $n-1$ 通り.
A の移動先にいる人物を B として, いったん A と B の席を入れ替える.
- (i)
- 最後に A と B が入れ替わらない場合. 全員の席が替わる方法は, A 以外の $n-1$ 人全員の席が替わる $a_{n-1}$ 通りある.
- (ii)
- 最後に A と B が入れ替わる場合. 全員の席が替わる方法は, 残りの $n-2$ 人全員の席が替わる $a_{n-2}$ 通りある.
- (2)
- 次に, 数列 $\{ p_n\}$ の一般項を求める. 便宜的に $p_1 = 0$ と定める. $n$ 人が席替えをする方法は $n!$ 通りあるから, \[ p_n = \dfrac{a_n}{n!}\] である. $n \geqq 3$ のとき, $[1]$ の両辺を $n!$ で割ると, \[\begin{aligned} p_n &= \frac{(n-1)(a_{n-1}+a_{n-2})}{n!} \\ &= \frac{n-1}{n}\cdot\frac{a_{n-1}}{(n-1)!}+\frac{1}{n}\cdot\frac{a_{n-2}}{(n-2)!} \\ &= \left( 1-\frac{1}{n}\right) p_{n-1}+\frac{1}{n}p_{n-2} \\ p_n-p_{n-1} &= -\frac{1}{n}(p_{n-1}-p_{n-2}) \quad \cdots [2] \end{aligned}\] が得られる. $p_2-p_1 = \dfrac{1}{2} \neq 0,$ $[2]$ と数学的帰納法により, \[ p_n-p_{n-1} \neq 0\] である. $[2]$ において $n$ を $3$ 以上 $n$ 以下の各整数に置き換えながら辺々を掛け合わせて $p_k-p_{k-1}$ $(3 \leqq k \leqq n-1)$ で割ると, \[ p_n-p_{n-1} = (-1)^{n-2}\frac{p_2-p_1}{n(n-1)\cdots 3} = \frac{(-1)^n}{n!}\] となる. $0! = 1$ であるから, $n \geqq 2$ のとき \[ p_n = \sum\limits_{k = 0}^n\frac{(-1)^k}{k!}\] が成り立つ.
- (3)
- 数列 $\{ p_n\}$ の最大値, 最小値を求める. \[\begin{aligned} (-1)^k\frac{1}{k!}+(-1)^{k+1}\frac{1}{(k+1)!} &= (-1)^k\frac{(k+1)-1}{(k+1)!} \\ &= (-1)^k\frac{k}{(k+1)!} \end{aligned}\] は $k$ が偶数のとき正, $k$ が奇数のとき負であるから, $\{ p_{2n}\}$ は単調増加, $\{ p_{2n-1}\}$ は単調減少である. よって, $n \geqq 2$ において $p_n$ は, $n = 2$ のとき最大値 $\dfrac{1}{2},$ $n = 3$ のとき最小値 $\dfrac{1}{2}-\dfrac{1}{3!} = \dfrac{1}{3}$ をとる.
- (4)
- 数列 $\{ p_n\}$ の極限値を求める. 指数関数のマクローリン展開 \[ e^x = \displaystyle\sum_{n = 0}^\infty\frac{x^n}{n!}\] (こちらを参照) から, \[\lim_{n \to \infty}p_n = \sum_{n = 0}^\infty\frac{(-1)^n}{n!} = e^{-1} = \frac{1}{e}\] である.
参考
- それぞれをもとの位置と異なる位置に並べ替える順列は「完全順列」または「攪乱順列」(derangement) と呼ばれる. $n$ 個のものの「完全順列」の総数は「モンモール数」(Montmort number) と呼ばれ, $!n$ で表すことが多い ($n \leqq 15$ のときの値はこちらを参照). その値 \[ !n = n!\sum\limits_{k = 0}^n\frac{(-1)^k}{k!}\] を求める問題は「モンモールの問題」として知られている.
- $n$ 個のものの順列全体に占める「完全順列」の割合は, $n$ が大きくなるにつれて \[\frac{1}{e} = 0.3678794411\cdots\] に近づいていく.
クイズ《番勝負が最終戦までもつれ込む確率》
A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行うとき, 対戦が最終戦までもつれ込む確率はいくらか.
ただし, A, B の実力は互角であり, 引き分けはないとする.
(オリジナル)
答え
$\dfrac{n}{2n-1}.$
解説
- (1)
- まず, 最終戦までもつれ込む場合の数を求める. 最終戦で A が優勝するには第 $2n-2$ 戦目までに A が $n-1$ 勝して最終戦で A が勝てばよいから, その場合の数は ${}_{2n-2}\mathrm C_{n-1}$ である. 最終戦で B が優勝する場合の数もこれに等しい. よって, 最終戦までもつれ込む場合の数は, \[ 2\cdot{}_{2n-2}\mathrm C_{n-1} \quad \cdots [1]\] である.
- (2)
- 次に, A, B の勝ち星の取り方の総数を求める. 第 $m$ 戦 $(n \leqq m \leqq 2n-1)$ で A が優勝するには第 $m-1$ 戦までに A が $n-1$ 勝して第 $m$ 戦で勝てばよいから, その場合の数は ${}_{m-1}\mathrm C_{n-1}$ である. 第 $m$ 戦で B が優勝する場合の数もこれに等しい. よって, A, B の勝ち星の取り方の総数は, \[ 2\sum_{m = n}^{2n-1}{}_{m-1}\mathrm C_{n-1} = 2\sum_{k = n-1}^{2n-2}{}_k\mathrm C_{n-1} = 2\cdot{}_{2n-1}\mathrm C_n \quad \cdots [2]\] である. ここで,「ホッケー・スティック恒等式」 \[\sum\limits_{k = r}^N{}_k\mathrm C_r = {}_{N+1}\mathrm C_{r+1}\] を使った (こちらを参照).
- (3)
- $[1]\div [2]$ から, 求める確率は \[\frac{{}_{2n-2}\mathrm C_{n-1}}{{}_{2n-1}\mathrm C_n} = \frac{(2n-2)!}{(n-1)!(n-1)!}\div\frac{(2n-1)!}{n!(n-1)!} = \frac{n}{2n-1}\] である.
参考
\[\lim\limits_{n \to \infty}\frac{n}{2n-1} = \lim\limits_{n \to \infty}\frac{1}{2-\dfrac{1}{n}} = \frac{1}{2}\]
であるから, $n$ が大きくなるにつれて $2n-1$ 番勝負が最終戦までもつれ込む確率は $\dfrac{1}{2}$ に近づいていく.
クイズ《番勝負でリードを許さずに優勝する確率》
A, B の $2$ 人が $2n−1$ 番勝負 ($n$: 正の整数) を行うとき, A が B に $1$ 度もリードを許さずに優勝する確率はいくらか.
ただし, A, B の実力は互角であり, 引き分けはないとする.
(オリジナル)
答え
$\dfrac{1}{2n}.$
解説
- (1)
- A が B に $1$ 度もリードを許さずに優勝する場合の数は, 優勝者が決まった後は両者が $n$ 勝 $n$ 敗になるまで優勝者が勝ちを譲るという取り決めのもとで $2n$ 回の勝負をするとき, A の負けが先行しない場合の数に他ならず, $n$ 番目の「カタラン数」 \[ C_n = \frac{{}_{2n}\mathrm C_n}{n+1} = \frac{(2n)!}{(n+1)!n!} \quad \cdots [1]\] (こちらを参照) に等しい.
- (2)
- A, B の勝ち星の取り方の総数は, $0$ 以上 $n-1$ 以下の各整数 $l$ に対して, A が $n$ 勝 $l$ 敗で優勝する場合の数も B が $n$ 勝 $l$ 敗で優勝する場合の数も ${}_{n+l}\mathrm C_n$ であることから, \[\begin{aligned} 2\sum\limits_{l = 0}^{n-1}{}_{n+l}\mathrm C_n &= 2\sum\limits_{k = n}^{2n-1}{}_k\mathrm C_n = 2\cdot{}_{2n}\mathrm C_{n+1} \\ &= \frac{2(2n)!}{(n+1)!(n-1)!} \quad \cdots [2] \end{aligned}\] である. ここで, 前問でも使った「ホッケー・スティック恒等式」 \[\sum\limits_{k = r}^N{}_k\mathrm C_r = {}_{N+1}\mathrm C_{r+1}\] を使った (こちらを参照).
- (3)
- $[1]\div [2]$ から, 求める確率は, \[\frac{(2n)!}{(n+1)!n!}\div\frac{2(2n)!}{(n+1)!(n-1)!} = \frac{1}{2n}\] である.
参考
互いに区別のできない $2n$ 個のものを A, B に $1$ 個ずつ配っていき, 両者が合計 $n$ 個ずつもつようにするとき,
どの時点でも A の個数が B の個数を下回らないような場合の数 $C_n$ は, $n$ 番目の「カタラン数」(Catalan number) と呼ばれ,
\[ C_n = \frac{{}_{2n}\mathrm C_n}{n+1}\]
であることが知られている.
クイズ《ベルトランの投票問題》
選挙で A は $a$ 票を得て, B はそれより少ない $b$ 票を得た.
投票中にずっと A の得票数が B の得票数を上回っていた確率はいくらか.
ただし, どの順序で投票されることも同様に確からしいとする.
(有名問題)
答え
$\dfrac{a-b}{a+b}.$
解説
座標平面上の点 $\mathrm P$ は, 原点から点 $(a,b)$ まで, A が $1$ 票を得るごとに $x$ 軸正方向に $1$ だけ進み, B が $1$ 票を得るごとに $y$ 軸正方向に $1$ だけ進むとする.
 投票中にずっと A の得票数が B の得票数を上回る場合の数は, 点 $\mathrm P$ が点 $(1,0)$ から点 $(a,b)$ まで直線 $y = x$ と共有点をもたないように進む経路の数に等しい.
点 $(1,0)$ から点 $(a,b)$ までの経路の数は ${}_{a+b-1}\mathrm C_{a-1}$ 通り.
そのうち直線 $y = x$ と共有点をもつ経路を直線 $y = x$ に関して折り返すと点 $(0,1)$ から点 $(a,b)$ まで進む経路になるから, そのような経路の数は ${}_{a+b-1}\mathrm C_{b-1}$ 通り.
また, 点 $\mathrm P$ の経路の総数は ${}_{a+b}\mathrm C_a$ 通り.
ゆえに, 求める確率は
\[\begin{aligned}
&\frac{{}_{a+b-1}\mathrm C_{a-1}-{}_{a+b-1}\mathrm C_{b-1}}{{}_{a+b}\mathrm C_a} \\
&= \left\{\frac{(a+b-1)!}{(a-1)!b!}-\frac{(a+b-1)!}{a!(b-1)!}\right\}\div\frac{(a+b)!}{a!b!} \\
&= \frac{a-b}{a+b}
\end{aligned}\]
である.
投票中にずっと A の得票数が B の得票数を上回る場合の数は, 点 $\mathrm P$ が点 $(1,0)$ から点 $(a,b)$ まで直線 $y = x$ と共有点をもたないように進む経路の数に等しい.
点 $(1,0)$ から点 $(a,b)$ までの経路の数は ${}_{a+b-1}\mathrm C_{a-1}$ 通り.
そのうち直線 $y = x$ と共有点をもつ経路を直線 $y = x$ に関して折り返すと点 $(0,1)$ から点 $(a,b)$ まで進む経路になるから, そのような経路の数は ${}_{a+b-1}\mathrm C_{b-1}$ 通り.
また, 点 $\mathrm P$ の経路の総数は ${}_{a+b}\mathrm C_a$ 通り.
ゆえに, 求める確率は
\[\begin{aligned}
&\frac{{}_{a+b-1}\mathrm C_{a-1}-{}_{a+b-1}\mathrm C_{b-1}}{{}_{a+b}\mathrm C_a} \\
&= \left\{\frac{(a+b-1)!}{(a-1)!b!}-\frac{(a+b-1)!}{a!(b-1)!}\right\}\div\frac{(a+b)!}{a!b!} \\
&= \frac{a-b}{a+b}
\end{aligned}\]
である.

参考
この問題は $1887$ 年に J・ベルトランによって定式化され, D・アンドレによって解決された (参考: G・ブロム, L・ホルスト, D・サンデル『確率論へようこそ』).
クイズ《弦の交点の個数》
円に互いに平行でない $n$ 本の弦を引くとき, 交点の個数は最大でいくらになるか.
(有名問題)
答え
$\dfrac{(n-1)n}{2}$ 個.
解説
円に互いに平行でない $n$ 本の弦を引く.
円は動かさずに, 弦を延長した直線のみを縮小, 平行移動することにより, 交点を円の中に収めることができる.
 よって, 求める個数は, 互いに平行でない $n$ 本の直線の交点の個数 $a_n$ に等しい.
互いに平行でない $2$ 本の直線は $1$ 点で交わるから, 新たにそれらに平行でない $1$ 本の直線をかくとき, 交点は $n$ 個増える.
よって, 求める個数は, 互いに平行でない $n$ 本の直線の交点の個数 $a_n$ に等しい.
互いに平行でない $2$ 本の直線は $1$ 点で交わるから, 新たにそれらに平行でない $1$ 本の直線をかくとき, 交点は $n$ 個増える.
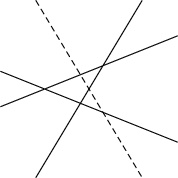 つまり,
\[ a_{n+1}-a_n = n\]
が成り立つ.
よって, $n \geqq 2$ のとき,
\[ a_n = \sum_{k = 1}^{n-1}k = \frac{(n-1)n}{2}\]
が成り立つ.
$a_1 = 0$ であるから, これは $n = 1$ のときも成り立つ.
つまり,
\[ a_{n+1}-a_n = n\]
が成り立つ.
よって, $n \geqq 2$ のとき,
\[ a_n = \sum_{k = 1}^{n-1}k = \frac{(n-1)n}{2}\]
が成り立つ.
$a_1 = 0$ であるから, これは $n = 1$ のときも成り立つ.
ゆえに, 求める個数は
である.


ゆえに, 求める個数は
| $\dfrac{(n-1)n}{2}$ 個 |
クイズ《ケーキ数》
A, B の $2$ 人がそれぞれ $1$ ホールのケーキを切り分ける.
A は毎回ピースを一列に並べ直してから切り, B はケーキを固定したまま切る.
できるだけ多くのピースに切り分けるとき, ピースの個数で A が B を上回るのは, 何回ナイフを入れたときか.
ただし, ナイフは空間内のどの方向にでも真っすぐに入れられるものとし, $1$ 回の入刀で切断面が通るピースをすべて切り分けるものとする.
(オリジナル)
答え
$4$ 回以上.
解説
A, B の切り分け方で, $n$ 回ナイフを入れたときにできるピースの個数をそれぞれ $a_n,$ $b_n$ とおく.
- (1)
- A の切り分け方では, ナイフを入れる度に各ピースが $2$ 個のピースに分かれるから, $a_n = 2^n$ である.
- (2)
- B の切り分け方では, $n$ 回ナイフを入れた状態から新たに $1$ 回ナイフを入れていくと, 新たな切断面が既存の切断面との交線 $n$ 本により分割されてできる平面領域の個数 $p_n$ だけピースが増える.
- (i)
- まず, $1$ つの面が $n$ 本の直線により分割されてできる領域の個数の最大値 $p_n$ を求める.
$n$ 本の直線をかいた状態から新たに $1$ 本の直線をかいていくと, 既存の直線と交わる度に領域が $1$ 個ずつ増え, 全部で $n+1$ 個の平面領域が増えるので,
\[ p_{n+1}-p_n = n+1\]
が成り立つ.
また, $p_1 = 2$ であるから, $n \geqq 2$ のとき \[\begin{aligned} p_n &= p_1+\sum_{k = 1}^{n-1}(p_{k+1}-p_k) \\ &= 2+\sum_{k = 1}^{n-1}(k+1) \\ &= 2+\frac{(n-1)n}{2}+(n-1) \\ &= \frac{1}{2}(n^2+n+2) \end{aligned}\] が成り立つ. これは $n = 1$ のときも成り立つ.

- (ii)
- 次に, $b_n$ を求める. 上記の考察により, \[ b_{n+1}-b_n = p_n = \frac{1}{2}(n^2+n+2)\] が成り立つ. また, $b_1 = 2$ であるから, $n \geqq 2$ のとき \[\begin{aligned} &b_n = b_1+\sum_{k = 1}^{n-1}(b_{k+1}-b_k) \\ &= 2+\sum_{k = 1}^{n-1}\frac{1}{2}(k^2+k+2) \\ &= 2+\frac{1}{2}\left(\sum_{k = 1}^{n-1}k^2+\sum_{k = 1}^{n-1}k+\sum_{k = 1}^{n-1}2\right) \\ &= 2+\frac{1}{2}\left\{\frac{1}{6}(n\!-\!1)n(2n\!-\!1)+\frac{1}{2}(n\!-\!1)n+2(n\!-\!1)\right\} \end{aligned}\] であり, 展開して整理すると, \[\begin{aligned} b_n &= \frac{1}{6}(n+1)(n^2-n+6) \end{aligned}\] が得られる. これは $n = 1$ のときも成り立つ.
- (3)
- 不等式 $a_n > b_n$ を解く. \[\begin{aligned} a_1 &= b_1 = 2, \quad a_2 = b_2 = 4, \quad a_3 = b_3 = 8, \\ a_4 &= 16 > 15 = b_4 \end{aligned}\] であるから, この不等式の最小の解は $n = 4$ である. さらに, 与えられた $4$ 以上の整数 $n$ に対して $a_n > b_n$ が成り立つとすると, \[ 2b_n-b_{n+1} = n(n-1)(n-2) > 0\] から得られる不等式 \[ 2 > \frac{b_{n+1}}{b_n}\] と辺々を掛け合わせることで \[ a_{n+1} = 2a_n > \frac{b_{n+1}}{b_n}\cdot b_n = b_{n+1}\] が得られる. よって, $a_n > b_n$ の解は $n \geqq 4$ である.
参考
- 数列 $\{ b_n\}$ の項は「ケーキ数」(cake number) と呼ばれる.
- ケーキを空間に置き換えても, $n$ 枚の平面により分割されてできる領域の個数の最大値 $b_n$ は上記の公式で与えられる. この公式を導く問題は「シュタイナーの分割問題」として知られている.