微分法による不等式の証明 (理系)
微分法による不等式の証明
不等式 $f(x) \geqq g(x)$ を示すには, 関数 $h(x) = f(x)-g(x)$ の最小値が $0$ 以上であることを示せばよい.
$h(x) \geqq 0$ を示すには, $h(x)$ の増減を調べる方法が有用である.
問題《ジョルダンの不等式》
$0 \leqq x \leqq \dfrac{\pi}{2}$ において
\[\frac{2}{\pi}x \leqq \sin x \leqq x\]
が成り立つことを示せ.
(参考: $2021$ 奈良教育大)
解答例
- 右側の不等式: $f(x) = x-\sin x$ とおく. $0 \leqq x \leqq \dfrac{\pi}{2}$ において, \[ f'(x) = 1-\cos x \geqq 0\] であるから, $f(x) \geqq f(0) = 0$ つまり $\sin x \leqq x$ が成り立つ.
- 左側の不等式: $g(x) = \sin x-\dfrac{2}{\pi}x$ とおく.
\[ g'(x) = \cos x-\frac{2}{\pi}\]
であるから, $0 \leqq x \leqq \dfrac{\pi}{2}$ において, $\cos x = \dfrac{2}{\pi}$ の解を $x = \alpha$ とおくと増減表は次のようになり, $g(x) \geqq g(0) = g\left(\dfrac{\pi}{2}\right) = 0$ が成り立つ.
$x$ $0$ $\cdots$ $\alpha$ $\cdots$ $\dfrac{\pi}{2}$ $g'(x)$ $+$ $0$ $-$ $g(x)$ $0$ $\nearrow$ 極大 $\searrow$ $0$
参考
- 不等式 $\dfrac{2}{\pi}x \leqq \sin x \leqq x$ $\left( 0 \leqq x \leqq \dfrac{\pi}{2}\right)$ は「ジョルダンの不等式」(Jordan's inequality) として知られている.
この不等式は, 次の図を使って証明することもできる.
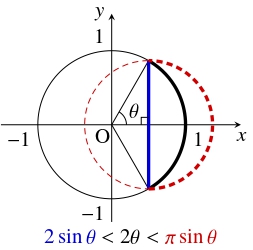
- 「ジョルダンの不等式」はさまざまな応用をもち, 例えば「バーゼル問題」(こちらを参照) を解くときに使われる.
- $\cos x = x$ を満たす実数 $x$ はただ $1$ つ存在し, その値 $x = 0.73908\cdots$ は「ドッティ数」(Dottie number) として知られている.
問題《対数関数と $1$ 次関数の比の極限》
次のことを示せ.
$2 < e < 4$ (こちらとこちらを参照) は, 証明なしに使ってよい.
- (1)
- $x < 2^x$ $(x \geqq 1)$ が成り立つ.
- (2)
- $\lim\limits_{x \to \infty}\dfrac{x}{e^x} = 0$ である.
- (3)
- $\lim\limits_{t \to \infty}\dfrac{\log t}{t} = 0$ である.
解答例
- (1)
- $f(x) = 2^x-x$ $(x \geqq 1)$ とおく. $x > 1$ において, $e < 4$ から \[\begin{aligned} f'(x) &= 2^x\log 2-1 \\ &> 2\log 2-1 = \log\frac{4}{e} > \log 1 = 0 \end{aligned}\] であるので, $f(x)$ は単調増加である. よって, $f(x)$ の連続性により, $x \geqq 1$ において \[ f(x) \geqq f(1) = 2-1 = 1 > 0\] が成り立つ. よって, $x < 2^x$ $(x \geqq 1)$ が成り立つ.
- (2)
- (1) により $x \geqq 1$ において \[ 0 < \frac{x}{e^x} < \frac{2^x}{e^x} = \left(\frac{2}{e}\right) ^x\] が成り立ち, $0 < \dfrac{2}{e} < 1$ から $x \to \infty$ のとき右辺は $0$ に収束するので, \[\lim\limits_{x \to \infty}\frac{x}{e^x} = 0\] である.
- (3)
- $t = e^x$ とおくと, $x = \log t$ であり, $x \to \infty$ のとき $t \to \infty$ となるから, \[\lim\limits_{t \to \infty}\dfrac{\log t}{t} = 0\] が成り立つ.
参考
一般に,「ロピタルの定理」(l'Hospital's rule) と呼ばれる, 次の定理が知られている:
$a$ が実数または $\infty,$ $-\infty$ のいずれかを表すとする.
関数 $f(x),$ $g(x)$ が $3$ つの条件
- $\lim\limits_{x \to a}f(x) = \lim\limits_{x \to a}g(x) = 0,$ $\pm\infty$
- $a$ の十分近くで $f(x),$ $g(x)$ は微分可能で, $\lim\limits_{x \to a}\dfrac{f'(x)}{g'(x)}$ が存在する
- $a$ の十分近くで, $x \neq a$ のとき, $g'(x) \neq 0$
問題《指数関数の近似とその応用》
$n$ を $2$ 以上の整数とする.
- (1)
- すべての実数 $x$ に対して $x \leqq e^{x-1}$ が成り立つことを示せ. また, 等号成立条件を求めよ.
- (2)
- 正の数 $x_1,$ $\cdots,$ $x_n$ が $x_1+\cdots +x_n = n$ を満たすとする. このとき, $x_1\cdots x_n \leqq 1$ が成り立つことを示せ. また, 等号成立条件を求めよ.
- (3)
- 正の数 $x_1,$ $\cdots,$ $x_n$ に対して, $a = \dfrac{x_1+\cdots +x_n}{n}$ とおく. このとき, \[ x_1\cdots x_n \leqq a^n\] が成り立つことを示せ. また, 等号成立条件を求めよ.
(参考: $2007$ 横浜市立大)
解答例
- (1)
- $f(x) = e^{x-1}-x$ とおく. このとき, $f'(x) = e^{x-1}-1$ から, \[ f'(x) \geqq 0 \iff x \geqq 1, \quad f'(x) \leqq 0 \iff x \leqq 1\] である. よって, $f(x)$ は $x = 1$ で極小かつ最小になるので, $f(x) \geqq f(1) = 0$ から $e^{x-1}-x \geqq 0$ つまり $x \leqq e^{x-1}$ であり, 等号成立は $x = 1$ の場合に限る.
- (2)
- (1) の結果から, \[ x_1\cdots x_n \leqq e^{x_1-1}\cdots e^{x_n-1} = e^{x_1+\cdots +x_n-n} = e^0 = 1\] であり, 等号成立は $x_1 = \cdots = x_n = 1$ の場合に限る.
- (3)
- $a = \dfrac{x_1+\cdots +x_n}{n}$ から $\dfrac{x_1}{a}+\cdots +\dfrac{x_n}{a} = n$ であるので, (2) の結果から
であり, 等号成立は $\dfrac{x_1}{a} = \cdots = \dfrac{x_n}{a} = 1$ つまり $x_1 = \cdots = x_n$ の場合に限る.
$\dfrac{x_1}{a}\cdots\dfrac{x_n}{a} \leqq 1$ つまり $x_1\cdots x_n \leqq a^n$
参考
- $x = a$ を含む開区間で, 何回でも微分可能な多くの重要な関数 $f(x)$ は, \[ f(x) = \sum_{n = 0}^\infty\frac{f^{(n)}(a)}{n!}(x-a)^n\] と表せる. ただし, $f^{(0)}(a) = f(a)$ と定める. この表示を $f(x)$ の $x = a$ の周りの「テイラー展開」(Taylor expansion) と呼ぶ. $a = 0$ のときは「マクローリン展開」(Maclaurin expansion) と呼ぶ. 例えば, 指数関数 $e^x$ は \[ e^x = \sum_{n = 0}^\infty\frac{x^n}{n!} \quad \cdots [*]\] と「マクローリン展開」されることが知られている. $[*]$ において, 右辺の $n = 1$ までの部分和を考えると, $e^x$ の $1$ 次関数による近似 $e^x \geqq 1+x$ が得られる. 本問では, $e^{x-1} \geqq 1+(x-1)$ を使って, $n$ 変数の相加・相乗平均の不等式を証明した.
- 相加・相乗平均の不等式の別証明については, こちらを参照されたい.
問題《関数の増減と相加・相乗平均の不等式》
$n$ を正の整数とする.
- (1)
- $s,$ $p$ を正の数とする. 関数 \[ f(x) = \frac{s+x}{n+1}-(px)^{\frac{1}{n+1}} \quad (x > 0)\] の最小値を求めよ.
- (2)
- 正の数 $a_1,$ $\cdots,$ $a_n$ に対して \[\frac{a_1+\cdots +a_n}{n} \geqq (a_1\cdots a_n)^{\frac{1}{n}} \quad \cdots [\ast ]\] が成り立つことを数学的帰納法で示せ.
解答例
- (1)
- 与式を $x$ で微分すると \[ f'(x) = \frac{1}{n+1}-p^{\frac{1}{n+1}}\cdot\frac{1}{n+1}x^{-\frac{n}{n+1}} = \frac{x^{\frac{n}{n+1}}-p^{\frac{1}{n+1}}}{(n+1)x^{\frac{n}{n+1}}}\] となるから, $f(x)$ は $x = p^{\frac{1}{n}}$ のとき極小かつ最小の値 \[\begin{aligned} f(p^{\frac{1}{n}}) &= \frac{s+p^{\frac{1}{n}}}{n+1}-(p^{1+\frac{1}{n}})^{\frac{1}{n+1}} \\ &= \frac{s+p^{\frac{1}{n}}}{n+1}-p^{\frac{1}{n}} = \frac{s-np^{\frac{1}{n}}}{n+1} \end{aligned}\] をとる.
- (2)
- (i)
- $n = 1$ のとき. $[\ast ]$ は明らかに成り立つ.
- (ii)
- $n = k$ ($k$: 正の整数) のとき $[\ast ]$ が成り立つとする. このとき, $s = a_1+\cdots +a_k,$ $p = a_1\cdots a_k$ に (1) の結果を適用すると, \[\begin{aligned} &\frac{s+x}{k+1}-(px)^{\frac{1}{k+1}} \geqq \frac{s-kp^{\frac{1}{k}}}{k+1} \\ &= \frac{k}{k+1}\left\{\frac{a_1+\cdots +a_k}{k}-(a_1\cdots a_k)^{\frac{1}{k}}\right\} \geqq 0 \end{aligned}\] となる. そこで, $x = a_{k+1}$ を代入すると, \[\begin{aligned} &\frac{s+a_{k+1}}{k+1}-(pa_{k+1})^{\frac{1}{k+1}} \geqq 0 \\ &\frac{a_1+\cdots +a_k+a_{k+1}}{k+1} \geqq (a_1\cdots a_ka_{k+1})^{\frac{1}{k+1}} \end{aligned}\] が得られる. よって, $n = k+1$ のとき $[*]$ が成り立つ.
参考
相加・相乗平均の不等式の別証明については, こちらを参照されたい.
問題《ヤングの不等式とその応用》
- (1)
- $0 < r < 1$ とする. $x > 0$ のとき, $r(x-1),$ $x^r-1$ の大小を比較せよ.
- (2)
- $p,$ $q > 1,$ $\dfrac{1}{p}+\dfrac{1}{q} = 1$ とする. $a,$ $b > 0$ のとき, $\dfrac{a}{p}+\dfrac{b}{q},$ $a^{\frac{1}{p}}b^{\frac{1}{q}}$ の大小を比較せよ.
- (3)
- $n$ を $2$ 以上の整数とする. $n$ 個の正の数 $x_1,$ $\cdots,$ $x_n$ に対して, $A_n = \dfrac{x_1+\cdots +x_n}{n},$ $G_n = (x_1\cdots x_n)^{\frac{1}{n}}$ とおくと, \[ A_{k+1} = \frac{kA_k+x_{k+1}}{k+1}, \quad G_{k+1} = G_k{}^{\frac{k}{k+1}}x_{k+1}{}^{\frac{1}{k+1}}\] が成り立つ. このことと (2) の結果を使って, \[ A_n \geqq G_n\] が成り立つことを示せ. また, 等号成立条件を求めよ.
(参考: $2019$ 九州歯科大, $2017$ 一橋大)
解答例
- (1)
- \[ f(x) = r(x-1)-(x^r-1) \quad (x > 0)\] とおく. これを $x$ で微分すると \[ f'(x) = r-rx^{r-1} = \frac{r(x^{1-r}-1)}{x^{1-r}}\] となるから, \[ f'(x) \geqq 0 \iff x \geqq 1, \quad f'(x) \leqq 0 \iff x \leqq 1\] である. よって, $f(x)$ は $x = 1$ において極小かつ最小の値をとるから, \[ f(x) \geqq f(1) = 0\] が成り立つ. ゆえに, \[ r(x-1) \geqq x^r-1 \quad \cdots [1]\] であり, 等号成立は $x = 1$ の場合に限る.
- (2)
- $r = \dfrac{1}{p}$ ($p > 1$ から $0 < x < 1$), $x = \dfrac{a}{b}$ ($a,$ $b > 0$ から $x > 0$) を $[1]$ に代入すると, \[\begin{aligned} \frac{1}{p}\left(\frac{a}{b}-1\right) &\geqq \left(\frac{a}{b}\right) ^{\frac{1}{p}}-1 \\ \frac{1}{p}(a-b) &\geqq a^{\frac{1}{p}}b^{-\frac{1}{p}}b-b \\ \frac{a}{p}+\left( 1-\frac{1}{p}\right) b &\geqq a^{\frac{1}{p}}b^{1-\frac{1}{p}} \\ \frac{a}{p}+\frac{b}{q} &\geqq a^{\frac{1}{p}}b^{\frac{1}{q}} \quad \cdots [2] \end{aligned}\] が得られる. 等号成立は, $\dfrac{a}{b} = 1$ つまり $a = b$ の場合に限る.
- (3)
- (i)
- $n = 2$ のとき. $a = x_1,$ $b = x_2,$ $p = q = 2$ に $[2]$ を適用すると, \[ A_2 = \frac{x_1}{2}+\frac{x_2}{2} \geqq x_1{}^{\frac{1}{2}}x_2{}^{\frac{1}{2}} = G_2\] が得られる. 等号成立は, $x_1 = x_2$ の場合に限る.
- (ii)
- $n = k$ ($k$: $2$ 以上の整数) のとき不等式が成り立ち, 等号成立が $x_1 = \cdots = x_k$ の場合に限るとする. このとき, $a = G_k,$ $b = x_{k+1},$ $p = \dfrac{k+1}{k},$ $q = k+1$ とおくと, $[2]$ から \[\begin{aligned} A_{k+1} &= \frac{kA_k+x_{k+1}}{k+1} \\ &\geqq \frac{kG_k+x_{k+1}}{k+1} = \frac{G_k}{\dfrac{k+1}{k}}+\frac{x_{k+1}}{k+1} = \frac{a}{p}+\frac{b}{q} \\ &\geqq a^{\frac{1}{p}}b^{\frac{1}{q}} = G_{k+1} \end{aligned}\] が得られる. 等号成立は, $A_k = G_k = x_{k+1}$ つまり $x_1 = \cdots = x_k = x_{k+1}$ の場合に限る.
参考
問題《ベルヌーイの不等式の一般化とその応用》
$n$ を $2$ 以上の整数とする.
- (1)
- $r < 0$ とする. \[ (1+x)^r \geqq 1+rx \quad (x > -1) \quad \cdots [1]\] が成り立つことを示せ. また, 等号成立条件を求めよ.
- (2)
- $a_1\cdots a_n = 1$ なる正の数 $a_1,$ $\cdots,$ $a_n$ に対して \[ a_1+\cdots +a_n \geqq n \quad \cdots [2]\] が成り立つことを示せ. また, 等号成立条件を求めよ.
- (3)
- 正の数 $x_1,$ $\cdots,$ $x_n$ に対して \[ x_1+\cdots +x_n \geqq n(x_1\cdots x_n)^{\frac{1}{n}} \quad \cdots [3]\] が成り立つことを示せ. また, 等号成立条件を求めよ.
解答例
- (1)
- $f(x) = (1+x)^r-(1+rx)$ とおく.
このとき,
\[ f'(x) = r(1+x)^{r-1}-r = r\{ (1+x)^{r-1}-1\}\]
である.
$r < 0$ であるから, $x > -1$ において
\[\begin{aligned}
f'(x) \geqq 0 &\iff (1+x)^{r-1}-1 \leqq 0 \iff (1+x)^{r-1} \leqq 1 \\
&\iff 1+x \geqq 1 \iff x \geqq 0, \\
f'(x) \leqq 0 &\iff -1 < x \leqq 0
\end{aligned}\]
が成り立つ.
よって, $f(x)$ の $x > -1$ における最小値は $f(0) = 0$ であるから, $f(x) \geqq 0$ $(x > -1)$ つまり $[1]$ が成り立つ. 等号成立は $x = 1$ の場合に限る.
$x$ $-1$ $\cdots$ $0$ $\cdots$ $f'(x)$ $-$ $0$ $+$ $f(x)$ $\searrow$ $0$ $\nearrow$ - (2)
- (i)
- $n = 2$ のとき. $a_1a_2 = 1$ から $a_2 = a_1{}^{-1}$ であるので, \[ (a_1+a_2)-2 = a_1+a_1{}^{-1}-2 = (\sqrt{a_1}-\sqrt{a_1}{}^{-1})^2 \geqq 0\] から $[2]$ が成り立つ. 等号成立は $a_1 = a_1{}^{-1} = a_2$ つまり $a_1 = a_2 = 1$ の場合に限る.
- (ii)
- $n = k$ ($k$: $2$ 以上の整数) のとき $[2]$ が成り立ち, 等号成立が $a_1 = \cdots = a_k$ の場合に限るとする. $n = k+1$ のとき, $a_1\cdots a_ka_{k+1} = 1$ から $a_1\cdots a_k = a_{k+1}{}^{-1}$ であるので, \[\begin{aligned} &a_1+\cdots +a_k+a_{k+1} \\ &\geqq k(a_1\cdots a_k)^{\frac{1}{k}}+a_{k+1} \\ &= ka_{k+1}{}^{-\frac{1}{k}}+a_{k+1} \\ &= k\left\{ 1+\left( a_{k+1}-1\right)\right\} ^{-\frac{1}{k}}+a_{k+1} \\ &\geqq k\left\{ 1+\left( -\frac{1}{k}\right) (a_{k+1}-1)\right\} +a_{k+1} \\ &= k+1 \end{aligned}\] が成り立つ. 第 $2$ の不等号は, $x = a_{k+1}-1\,(> -1),$ $r = -\dfrac{1}{k}\,(< 0)$ に $[1]$ を適用することで得られる. 等号成立は $a_1 = \cdots = a_k = a_{k+1} = 1$ の場合に限る.
- (3)
- $G_n = (x_1\cdots x_n)^{\frac{1}{n}},$ $a_k = \dfrac{x_k}{G_n}$ とおくと, $a_1\cdots a_n = 1$ となるから, $[2]$ により, \[\begin{aligned} \frac{x_1}{G_n}+\cdots +\frac{x_n}{G_n} &\geqq n \\ x_1+\cdots +x_n &\geqq nG_n \end{aligned}\] つまり $[3]$ が得られる. 等号成立は $x_1 = \cdots = x_n$ の場合に限る.
参考
- $[1]$ は,「ベルヌーイの不等式」(Bernoulli's inequality) と呼ばれ, よく知られている $r$ が正の整数の場合だけでなく, $r \leqq 0,$ $r \geqq 1$ の場合にも成り立つ.
- 相加・相乗平均の不等式の別証明については, こちらを参照されたい.
問題《円に内接する $n$ 角形の周長・面積の最大値》
- (1)
- $n$ を $2$ 以上の整数とし, $t_1,$ $\cdots,$ $t_n > 0,$ $t_1+\cdots +t_n = 1$ とする. $x_1,$ $\cdots,$ $x_n \in (0,\pi )$ のとき, \[\sin\left(\sum_{k = 1}^nt_kx_k\right) \geqq \sum_{k = 1}^nt_k\sin x_k\] が成り立つことを示せ. また, 等号成立は $x_1 = \cdots = x_n$ の場合に限ることを示せ.
- (2)
- $3$ 以上の整数 $n$ に対して, 単位円に内接する $n$ 角形のうち周の長さ $L$ が最大になるもの, 面積 $S$ が最大になるものは正 $n$ 角形であることを示せ.
(参考: $2022$ 大阪公立大)
解答例
- (1)
- (i)
- $n = 2$ のとき. $x_2$ を定数とみなして, $0 < x_1 < \pi$ の範囲で $x_1$ の関数 \[ f(x_1) = \sin (t_1x_1+t_2x_2)-t_1\sin x_1-t_2\sin x_2\] を考える. \[ f'(x_1) = t_1\{\cos (t_1x_1+t_2x_2)-\cos x_1\}\] であり, $\cos x$ $(0 < x < \pi )$ は単調減少であるから, $t_1x_1+t_2x_2 \leqq x_1$ つまり $x_1 \geqq x_2$ のとき $f'(x_1) \geqq 0$ であり, $t_1x_1+t_2x_2 \geqq x_1$ つまり $x_1 \leqq x_2$ のとき $f'(x_1) \leqq 0$ である. よって, $f(x_1) \geqq f(x_2) = 0$ であるから, \[\sin (t_1x_1+t_2x_2) \geqq t_1\sin x_1+t_2\sin x_2 \quad (0 < x_1 < \pi )\] が成り立ち, 等号成立は $x_1 = x_2$ の場合に限る.
- (ii)
- $n = m$ ($m$: $2$ 以上の整数) のとき不等式と等号成立条件が成り立つとする. $n = m+1$ の場合に, $s = t_1+\cdots +t_m$ とおく. \[ u_k = \frac{t_k}{s} \quad (1 \leqq k \leqq m)\] とおくと, \[\begin{aligned} &\sin\left(\sum_{k = 1}^{m+1}t_kx_k\right) \\ &= \sin\left(\sum_{k = 1}^mt_kx_k+t_{m+1}x_{m+1}\right) \\ &= \sin\left( s\sum_{k = 1}^mu_kx_k+t_{m+1}x_{m+1}\right) \\ &\geqq s\sin\left(\sum_{k = 1}^mu_kx_k\right) +t_{m+1}\sin x_{m+1} \quad (\because\text{(i)}) \\ &\geqq s\sum_{k = 1}^mu_k\sin x_k+t_{m+1}\sin x_{m+1} \\ &= \sum_{k = 1}^{m+1}t_k\sin x_k \end{aligned}\] が得られる. 等号成立は, “ $\displaystyle\sum\limits_{k = 1}^mu_kx_k = x_{m+1},$ $x_1 = \cdots = x_m$ ” つまり $x_1 = \cdots = x_m = x_{m+1}$ の場合に限る.
- (2)
- $n$ 角形 $\mathrm P_1\cdots\mathrm P_n$ が単位円 $\mathrm O$ に内接するとする. $\mathrm P_{n+1} = \mathrm P_1$ として, $\theta _k = \angle\mathrm P_k\mathrm{OP}_{k+1}$ とおく. \[\begin{aligned} L &= \sum_{k = 1}^n\mathrm P_k\mathrm P_{k+1} = \sum_{k = 1}^n2\sin\frac{\theta _k}{2} = 2n\sum_{k = 1}^n\frac{1}{n}\sin\frac{\theta _k}{2} \\ &\leqq 2n\sin\left(\sum_{k = 1}^n\frac{1}{n}\cdot\frac{\theta _k}{2}\right) = 2n\sin\frac{\pi}{n} \end{aligned}\] であり, 等号成立は $\dfrac{\theta _1}{2} = \cdots = \dfrac{\theta _n}{2}$ の場合に限るから, 単位円に内接する $n$ 角形のうち周の長さ $L$ が最大になるものは正 $n$ 角形である. \[\begin{aligned} S &= \sum_{k = 1}^n\triangle\mathrm{OP}_k\mathrm P_{k+1} = \sum_{k = 1}^n\frac{1}{2}\sin\theta _k = \frac{n}{2}\sum_{k = 1}^n\frac{\sin\theta _k}{n} \\ &\leqq \frac{n}{2}\sin\left(\sum_{k = 1}^n\frac{\theta _k}{n}\right) = \frac{n}{2}\sin\frac{2\pi}{n} \end{aligned}\] であり, 等号成立は $\theta _1 = \cdots = \theta _n$ の場合に限るから, 単位円に内接する $n$ 角形のうち面積 $S$ が最大になるものは正 $n$ 角形である.
参考
(1) の不等式は「イェンセンの不等式」(こちらを参照) である.
問題《$2^x = x^2$ の実数解》
次の問に答えよ.
$e < 4$ であること (こちらを参照) は証明なしに使ってよい.
- (1)
- $\dfrac{1}{2} < \log 2$ を示せ.
- (2)
- $x > 4$ において $f(x) = 2^x-x^2$ は単調増加であることを示せ.
- (3)
- $2^x = x^2$ の整数解をすべて求めよ.
- (4)
- $2^x = x^2$ は整数でない実数解を $1$ つもつ. その整数部分を求めよ.
解答例
- (1)
- $\log x$ の単調増加性, $e < 2^2$ から,
である.
$1 < 2\log 2$ つまり $\dfrac{1}{2} < \log 2$ - (2)
- $f(x) = 2^x-x^2$ から, \[\begin{aligned} f'(x) &= 2^x\log 2-2x, \\ f''(x) &= 2^x(\log 2)^2-2 \end{aligned}\] である. $2^x$ の単調増加性から, $x > 4$ のとき, \[\begin{aligned} f''(x) &> 2^4(\log 2)^2-2 \\ &> 2^4\left(\frac{1}{2}\right) ^2-2 = 2 \\ &> 0 \end{aligned}\] である. よって, $x > 4$ において $f'(x)$ は単調増加で, \[ f'(4) > 2^4\cdot\frac{1}{2}-2\cdot 4 = 0\] であるから, $x > 4$ において $f'(x) > 0$ が成り立つ. これは, $x > 4$ において $f(x)$ が単調増加であることを意味する.
- (3)
- (2) の結果と $f(4) = 2^4-4^2 = 0,$ $f(x)$ の連続性により, $x > 4$ において $f(x) > 0$ が成り立つ. また, $x \leqq -1$ において, $2^x,$ $-x^2$ は単調増加で, その和 $2^x-x^2$ も単調増加であるから, \[ f(x) \leqq f(-1) = 2^{-1}-(-1)^2 = -\frac{1}{2} < 0\] が成り立つ. さらに, \[ f(0) = 1, \quad f(1) = 1, \quad f(2) = 0, \quad f(3) = -1\] である. 以上から, $f(x) = 0$ つまり $2^x = x^2$ の整数解は $x = 2,$ $4$ に限る.
- (4)
- $f(x)$ は連続で $f(-1) < 0,$ $f(0) > 0$ であるから, 中間値の定理により $-1 < x < 0$ の範囲に $f(x) = 0$ つまり $2^x = x^2$ の実数解が存在する. ゆえに, 求める実数解の整数部分は $-1$ である.
参考
- $2^x = x^2$ の実数解は, $y = xe^x$ $(y \geqq -e^{-1})$ の「逆対応」として定まる「ランベルト $W$ 関数」(Lambert $W$ function) $W(x)$ $(x \geqq -e^{-1})$ を用いて \[ x = e^{-W(-\log\sqrt 2)},\ -e^{-W(\log\sqrt 2)}\] と表される. 実際, $x > 0$ のとき \[\begin{aligned} 2^x = x^2 &\iff x\log 2 = 2\log x \\ &\iff \frac{\log x}{x} = \frac{\log 2}{2} \\ &\iff -\log x\cdot e^{-\log x} = -\log\sqrt 2 \\ &\iff W(-\log x\cdot e^{-\log x}) = W( -\log\sqrt 2) \\ &\iff -\log x = W(-\log\sqrt 2) \\ &\iff x = e^{-W(-\log\sqrt 2)} \end{aligned}\] となり, $x < 0$ のとき \[\begin{aligned} 2^x = x^2 &\iff x\log 2 = 2\log (-x) \\ &\iff -\frac{\log (-x)}{-x} = \frac{\log 2}{2} \\ &\iff -\log (-x)\cdot e^{-\log (-x)} = \log\sqrt 2 \\ &\iff W(-\log (-x)\cdot e^{-\log (-x)}) = W(\log\sqrt 2) \\ &\iff -\log (-x) = W(\log\sqrt 2) \\ &\iff x = -e^{-W(\log\sqrt 2)} \end{aligned}\] となるからである. $-e^{-1} < x < 0$ のとき $x$ に対応する $W(x)$ の値は $2$ つあるため (こちらを参照), $x = e^{-W(-\log\sqrt 2)}$ は $2$ つの解 $x = 2,$ $4$ を表している. $y = W(x)$ のように, $1$ つの $x$ の値に $1$ つ以上の $y$ の値が対応しているとき, $y$ を $x$ の「多価関数」(multivalued function) と呼ぶ.
- $2^x = x^2$ の整数解を求める解法については, こちらも参照されたい.
問題《三角関数のマクローリン展開にまつわる不等式》
- (1)
- 各非負整数 $n$ に対して, 関数 $f_n(x)$ を \[ f_n(x) = \sum_{k = 0}^{2n}\frac{(-1)^k}{(2k+1)!}x^{2k+1}-\sin x\] で定める. $n \geqq 1$ のとき, $f_n{}'(x),$ $f_n{}''(x),$ $f_n{}'''(x),$ $f_n{}''''(x)$ を求めよ.
- (2)
- $n$ を正の整数とする. $x \geqq 0$ において \[\begin{aligned} \sum_{k = 0}^{2n-1}\frac{(-1)^k}{(2k)!}x^{2k} &\leqq \cos x \leqq \sum_{k = 0}^{2n}\frac{(-1)^k}{(2k)!}x^{2k}, \\ \sum_{k = 0}^{2n-1}\frac{(-1)^k}{(2k+1)!}x^{2k+1} &\leqq \sin x \leqq \sum_{k = 0}^{2n}\frac{(-1)^k}{(2k+1)!}x^{2k+1} \end{aligned}\] が成り立つことを示せ.
解答例
- (1)
- $f_n(x)$ を $4$ 回微分すると, \[\begin{aligned} f_n{}'(x) &= \sum_{k = 0}^{2n}\frac{(-1)^k}{(2k)!}x^{2k}-\cos x, \\ f_n{}''(x) &= \sum_{k = 1}^{2n}\frac{(-1)^k}{(2k-1)!}x^{2k-1}+\sin x \\ &= \sin x-\sum_{k = 0}^{2n-1}\frac{(-1)^k}{(2k+1)!}x^{2k+1}, \\ f_n{}'''(x) &= \cos x-\sum_{k = 0}^{2n-1}\frac{(-1)^k}{(2k)!}x^{2k}, \\ f_n{}''''(x) &= -\sin x-\sum_{k = 1}^{2n-1}\frac{(-1)^k}{(2k-1)!}x^{2k-1} \\ &= \sum_{k = 0}^{2n-2}\frac{(-1)^k}{(2k+1)!}x^{2k+1}-\sin x = f_{n-1}(x) \end{aligned}\] が得られる.
- (2)
- (i)
- $n = 1$ のとき.
(1) の結果により,
\[\begin{aligned}
f_1{}''''(x) &= f_0(x) = x-\sin x, \\
f_0{}'(x) &= 1-\cos x \geqq 0
\end{aligned}\]
が成り立つ.
よって, $x \geqq 0$ において,
- $f_1{}''''(x)$ は単調増加であるから \[ f_1{}''''(x) \geqq f_1{}''''(0) = 0,\]
- $f_1{}'''(x)$ は単調増加であるから \[ f_1{}'''(x) \geqq f_1{}'''(0) = 0,\]
- $f_1{}''(x)$ は単調増加であるから \[ f_1{}''(x) \geqq f_1{}''(0) = 0,\]
- $f_1{}'(x)$ は単調増加であるから \[ f_1{}'(x) \geqq f_1{}'(0) = 0,\]
- $f_1(x)$ は単調増加であるから \[ f_1(x) \geqq f_1(0) = 0\]
- (ii)
- $n > 1$ のとき. $x \geqq 0$ において $f_{n-1}(x) \geqq 0,$ $f_{n-1}{}'(x) \geqq 0,$ $f_{n-1}{}''(x) \geqq 0,$ $f_{n-1}{}'''(x) \geqq 0$ であるとすると, (1) と同様に, $x \geqq 0$ において $f_n(x) \geqq 0,$ $f_n{}'(x) \geqq 0,$ $f_n{}''(x) \geqq 0,$ $f_n{}'''(x) \geqq 0$ となる.
参考
$\cos x,$ $\sin x$ は
\[\cos x = \sum_{n = 0}^\infty\frac{(-1)^n}{(2n)!}x^{2n}, \quad \sin x = \sum_{n = 0}^\infty\frac{(-1)^n}{(2n+1)!}x^{2n+1}\]
と「マクローリン展開」される (こちらを参照).
問題《平方根の和と和の平方根に関する不等式》
$a,$ $b$ を正の数とする.
すべての正の数 $x,$ $y$ に対して
\[ a\sqrt x+b\sqrt y \leqq c\sqrt{x+y}\]
が成り立つような実数 $c$ の最小値を, $a,$ $b$ を用いて表せ.
(参考: $1995$ 東京大)
解答例
$x,$ $y > 0$ として, $t = \dfrac{y}{x}\,(> 0)$ とおく.
\[\begin{aligned}
a\sqrt x+b\sqrt y \leqq c\sqrt{x+y} &\iff a+b\sqrt t \leqq c\sqrt{1+t} \\
&\iff \frac{a+b\sqrt t}{\sqrt{1+t}} \leqq c
\end{aligned}\]
であるから, 求める $c$ の値は関数 $f(t) = \dfrac{a+b\sqrt t}{\sqrt{1+t}}$ の最大値に等しい.
\[\begin{aligned}
f'(t) &= \frac{\dfrac{b}{2\sqrt t}\cdot\sqrt{1+t}-(a+b\sqrt t)\cdot\dfrac{1}{2\sqrt{1+t}}}{1+t} \\
&= \frac{b(1+t)-(a+b\sqrt t)\sqrt t}{2\sqrt t(1+t)^{\frac{3}{2}}} = \frac{b-a\sqrt t}{2\sqrt t(1+t)^{\frac{3}{2}}}
\end{aligned}\]
であるから,
\[\begin{aligned}
f'(t) \geqq 0 &\iff 0 < t \leqq \frac{b^2}{a^2}, \\
f'(t) \leqq 0 &\iff t \geqq \frac{b^2}{a^2}
\end{aligned}\]
が成り立つ.
よって, $t = \dfrac{b^2}{a^2}$ のとき, $f(t)$ は極大かつ最大の値
\[\frac{a+b\sqrt{\dfrac{b^2}{a^2}}}{\sqrt{1+\dfrac{b^2}{a^2}}} = \frac{a^2+b^2}{\sqrt{a^2+b^2}} = \sqrt{a^2+b^2}\]
をとる.
ゆえに, 求める値は $c = \sqrt{a^2+b^2}$ である.
| $t$ | $0$ | $\cdots$ | $\dfrac{b^2}{a^2}$ | $\cdots$ |
| $f'(t)$ | $+$ | $0$ | $-$ | |
| $f(t)$ | $\nearrow$ | 極大 | $\searrow$ |
参考
「コーシー=シュワルツの不等式」を利用した別証明については, こちらを参照されたい.
問題《階乗数である最大の高度合成数》
正の整数 $a$ の正の約数の個数を $d(a)$ で表す.
正の整数 $N$ が $0 < a < N$ なるすべての整数 $a$ に対して $d(a) < d(N)$ を満たすとき, $N$ を「高度合成数」と呼ぶ.
正の整数 $n$ に対して, $1 \leqq n \leqq 7$ のとき $n!$ は「高度合成数」であることが知られている.
以下, $n!$ が
と素因数分解されるとする.
| $n! = 2^{e_1}3^{e_2}5^{e_3}7^{e_4}\cdots p_r{}^{e_r}$ |
| ($p_i$: $i$ 番目に小さい素数, $e_i$: 正の整数) |
- (1)
- $d(27720),$ $d(8!),$ $d(166320),$ $d(9!)$ の値を求め, $8!$ と $9!$ は「高度合成数」でないことを示せ.
- (2)
- $n \geqq 4$ のとき, $e_1,$ $\cdots,$ $e_r$ を用いて $d(n!),$ $d\left(\dfrac{7}{8}n!\right)$ を表せ.
- (3)
- $n \geqq 2$ のとき $e_1 > n-2-\log _2n,$ $n \geqq 7$ のとき $e_4 < \dfrac{n}{6}$ が成り立つことを示せ. 各番号 $i$ $(1 \leqq i \leqq r)$ に対して \[ e_i = \sum_{k = 1}^{\left[\log _{p_i}n\right]}\left[\frac{n}{p_i{}^k}\right] \quad \cdots [\ast ]\] であること (こちらを参照) は証明なしに用いてよい. ここで, 実数 $x$ を超えない最大の整数を $[x]$ で表す.
- (4)
- $n \geqq 24$ のとき $n-14-2\log _2n > 0$ が成り立つことを示せ.
- (5)
- $n \geqq 10$ のときの $d(n!),$ $d\left(\dfrac{7}{8}n!\right)$ の値を比較することにより, $n!$ $(n \geqq 1)$ の形の最大の「高度合成数」は $7!$ であることを示せ.
解答例
- (1)
- $\;\:27720 = 2^3\cdot 3^2\cdot 5\cdot 7\cdot 11,$ $8! = 2^7\cdot 3^2\cdot 5\cdot 7,$
$166320 = 2^4\cdot 3^3\cdot 5\cdot 7\cdot 11,$ $9! = 2^7\cdot 3^4\cdot 5\cdot 7$ から \[\begin{aligned} d(27720) &= (3+1)(2+1)(1+1)(1+1)(1+1) = 96, \\ d(8!) &= (7+1)(2+1)(1+1)(1+1) = 96, \\ d(166320) &= (4+1)(3+1)(1+1)(1+1)(1+1) = 160, \\ d(9!) &= (7+1)(4+1)(1+1)(1+1) = 150 \end{aligned}\] よって \[ d(25200) = d(8!), \quad d(166320) > d(9!)\] であるので, $8! = 40320,$ $9! = 362880$ は「高度合成数」でない. - (2)
- 約数の個数の公式により, \[ d(n!) = (e_1+1)(e_2+1)(e_3+1)(e_4+1)(e_5+1)\cdots (e_r+1)\] が成り立つ. 同様に, $n \geqq 4$ のとき, \[\frac{7}{8}n! = 2^{e_1-3}3^{e_2}5^{e_3}7^{e_4+1}11^{e_5}\cdots p_r{}^{e_r}\] から \[ d\!\left(\frac{7}{8}n!\right)\! = (e_1\!-2)(e_2\!+1)(e_3\!+1)(e_4\!+2)(e_5\!+1)\cdots (e_r\!+1)\] が成り立つ.
- (3)
- $n \geqq 2$ のとき, 公式 $[\ast ],$ 等比数列の和の公式により, \[\begin{aligned} e_1 &= \sum_{k = 1}^{[\log _2n]}\left[\frac{n}{2^k}\right] \\ &> \sum_{k = 1}^{[\log _2n]}\left(\frac{n}{2^k}-1\right) \quad (\because [x] > x-1) \\ &= \frac{n}{2}\left( 1-\frac{1}{2^{[\log _2n]}}\right)\div\left(1-\frac{1}{2}\right) -[\log _2n] \\ &= n-\frac{n}{2^{[\log _2n]}}-[\log _2n] \\ &> n-2-\log _2n \end{aligned}\] が成り立つ. ここで, 最後の不等号は, $[\log _2n] \leqq \log _2n$ と, $\log _2n < [\log _2n]+1$ から $n < 2^{[\log _2n]+1}$ よって $\dfrac{n}{2^{[\log _2n]}} < 2$ であることから従う.
- $n \geqq 7$ のとき, 公式 $[\ast ],$ 等比数列の和の公式により, \[\begin{aligned} e_4 &= \sum_{k = 1}^{[\log _7n]}\left[\frac{n}{7^k}\right] \\ &\leqq \sum_{k = 1}^{[\log _7n]}\frac{n}{7^k} \quad (\because [x] \leqq x) \\ &= \frac{n}{7}\left( 1-\frac{1}{7^{[\log _7n]}}\right)\div\left(1-\frac{1}{7}\right) \\ &< \frac{n}{6} \end{aligned}\] が成り立つ.
- (4)
- $f(x) = x-14-2\log _2x$ $(x > 0)$ とおく.
\[ f'(x) = 1-\frac{2}{x\log 2}\]
であるから,
\[ f'(x) \geqq 0 \iff 1 \geqq \frac{2}{x\log 2} \iff x \geqq \frac{2}{\log 2}\]
が成り立つ.
よって, $f(x)$ は $x \geqq \dfrac{2}{\log 2}$ において単調に増加する.
特に, $e < 4$ から
であるので, $f(x)$ は $x \geqq 4$ において単調に増加する. さらに, \[ f(24) = 10-2\log _2{24} = 2(\log _2{32}-\log _2{24}) > 0\] であるから, $x \geqq 24$ のとき $f(x) > 0$ が成り立つ. ゆえに, \[ n-14-2\log _2n > 0 \quad (n \geqq 24)\] が成り立つ.$\sqrt e < 2$ よって $4 = \dfrac{2}{\log\sqrt e} > \dfrac{2}{\log 2}$ - (5)
- (1) から, $n \geqq 10$ のとき
\[ d\left(\frac{7}{8}n!\right) \geqq d(n!) \quad \cdots [1]\]
が成り立つことを示せば十分である.
(2) の結果から ,
\[\begin{aligned}
[1] &\iff (e_1-2)(e_4+2) \geqq (e_1+1)(e_4+1) \\
&\iff e_1e_4+2e_1-2e_4-4 \geqq e_1e_4+e_1+e_4+1 \\
&\iff e_1 \geqq 3e_4+5\ \cdots [1]'
\end{aligned}\]
が成り立つ.
以下, $n$ について $e_1,$ $e_4$ は広義単調増加である ($n$ が大きくなって $e_1,$ $e_4$ が小さくなることはない) ことに注意する.
- (i)
- $10 \leqq n \leqq 13$ のとき. $10!$ の素因数分解における $2$ の指数は $8,$ $n!$ の素因数分解における $7$ の指数は $1$ であるから, \[ e_1 \geqq 8 = 3\cdot 1+5 = 3e_4+5\] が成り立つ.
- (ii)
- $14 \leqq n \leqq 20$ のとき. $14!$ の素因数分解における $2$ の指数は $11,$ $n!$ の素因数分解における $7$ の指数は $2$ であるから, \[ e_1 \geqq 11 = 3\cdot 2+5 = 3e_4+5\] が成り立つ.
- (iii)
- $21 \leqq n \leqq 23$ のとき. $21!$ の素因数分解における $2$ の指数は $18,$ $n!$ の素因数分解における $7$ の指数は $3$ であるから, \[ e_1 \geqq 18 > 14 = 3\cdot 3+5 = 3e_4+5\] が成り立つ.
- (iv)
- $n \geqq 24$ のとき. (4) の結果から \[\begin{aligned} e_1-(3e_4+5) &> (n-2-\log _2n)-\left( 3\cdot\frac{n}{6}+5\right) \\ &= \frac{1}{2}(n-14-2\log _2n) \\ &> 0 \end{aligned}\] が成り立つ.
別解
- (4)
- $f(n) = n-14-2\log _2n$ ($n$: 正の整数) とおく.
このとき,
\[\begin{aligned}
&f(n+1)-f(n) \\
&= \{ (n+1)-14-2\log _2(n+1)\} -(n-14-2\log _2n) \\
&= 1-2\log _2(n+1)+2\log _2n \\
&= \log _2\frac{2n^2}{(n+1)^2}
\end{aligned}\]
である.
$n > 1+\sqrt 2$ のとき
したがって$2n^2\!-(n+1)^2\! = (n-1)^2\!-2 > 0$ つまり $\dfrac{2n^2}{(n+1)^2} > 1$
が成り立つから, $n > 1+\sqrt 2$ において $f(n)$ は単調に増加する. \[ f(24) = 10-2\log _2{24} = 2(\log _2{32}-\log _2{24}) > 0\] であるから, $n \geqq 24$ のとき $f(n) > 0$ が成り立つ. ゆえに, \[ n-14-2\log _2n > 0 \quad (n \geqq 24)\] が成り立つ.$f(n+1)-f(n) > 0$ つまり $f(n+1) > f(n)$
参考
- 正の整数 $N$ が $N$ 未満のどの正の整数よりも多くの正の約数をもつとき, $N$ を「高度合成数」(highly composite number) と呼ぶ.
「高度合成数」を小さい順に列挙すると $1,$ $2,$ $4,$ $6,$ $12,$ $24,$ $36,$ $48,$ $60,$ $120,$ $180,$ $240,$ $360,$ $\cdots$ となる.
約数が多いと便利なため,
“ $1$ 日$= 24$ 時間 ” の $24,$“ $1$ 時間$= 60$ 分 ” の $60,$“ $1$ 周$= 360^\circ$ ” の $360$ など,「高度合成数」の多くが度量衡に利用されている. - 「高度合成数」の性質については, こちらを参照されたい.
- $[\ast ]$ は初等整数論における「ルジャンドルの公式」(Legendre's formula) として知られている.
