速度・加速度
速度
定義《直線・平面・空間における動点の速度》
$n$ 次元空間において, 動点 $\mathrm P(x_1,\cdots,x_n)$ の座標 $x_1,$ $\cdots,$ $x_n$ が時刻 $t$ の関数として微分可能であるとする.
このとき, 時刻 $t$ における点 $\mathrm P$ の速度 $\vec v$ を
\[\vec v = \left(\frac{dx_1}{dt},\cdots,\frac{dx_n}{dt}\right),\]
速さ $|\vec v|$ を
\[ |\vec v| = \sqrt{\left(\frac{dx_1}{dt}\right) ^2+\cdots +\left(\frac{dx_n}{dt}\right) ^2}\]
で定める.
問題《斜方投射における物体の速度》
広い平地において, 速さ $v_0$ で地面から角 $\theta$ をなす方向に投げられた物体の時刻 $t$ における位置 $(x,y)$ は, 空気抵抗がないとき, 定数 $g\,(> 0)$ を用いて
\[ x = v_0\cos\theta\cdot t, \quad y = v_0\sin\theta\cdot t-\frac{1}{2}gt^2\]
と表されるという.
この物体が地面に落下する直前の速さも $v_0$ であることを確かめよ.
解答例
物体が地面に落下する時刻は,
\[ v_0\sin\theta\cdot t-\frac{1}{2}gt^2 = 0, \quad t \neq 0\]
の解
\[ t = \frac{2v_0\sin\theta}{g}\]
である.
この物体の速度ベクトルは, 時刻 $t$ において
\[\left(\frac{dx}{dt},\frac{dy}{dt}\right) = (v_0\cos\theta,v_0\sin\theta -gt),\]
落下時において
\[ (v_0\cos\theta,-v_0\sin\theta )\]
である.
よって, 求める速さは
\[\sqrt{(v_0\cos\theta )^2+(-v_0\sin\theta )^2} = v_0\]
である.
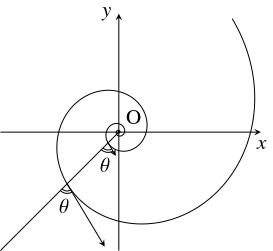
問題《等角らせんの性質》
$a$ を実数とする.
$xy$ 平面上を運動する点 $\mathrm P$ の時刻 $t$ における座標が
\[ x = e^{at}\cos t, \quad y = e^{at}\sin t \quad \cdots [*]\]
で表されるとする.
このとき, 原点を基点とする点 $\mathrm P$ の位置ベクトル $\vec p = (x,y)$ と点 $\mathrm P$ の速度ベクトル $\vec v = \left(\dfrac{dx}{dt},\dfrac{dy}{dt}\right)$ のなす角 $\theta$ は $t$ によらず一定であることを示せ.
(参考: $2000$ 神戸大)
解答例
$x = e^{at}\cos t,$ $y = e^{at}\sin t$ を $t$ で微分すると
\[\begin{aligned}
\frac{dx}{dt} &= ae^{at}\cos t-e^{at}\sin t = e^{at}(a\cos t-\sin t), \\
\frac{dy}{dt} &= ae^{at}\sin t+e^{at}\cos t = e^{at}(a\sin t+\cos t)
\end{aligned}\]
となるから,
\[\begin{aligned}
\vec p\cdot\vec v &= x\frac{dx}{dt}+y\frac{dy}{dt} \\
&= e^{2at}\{\cos t(a\cos t-\sin t)+\sin t(a\sin t+\cos t)\} \\
&= e^{2at}\cdot a(\cos ^2t+\sin ^2t) \\
&= ae^{2at}, \\
|\vec p| &= \sqrt{x^2+y^2} = e^{at}\sqrt{\cos ^2t+\sin ^2t} = e^{at}, \\
|\vec v| &= \sqrt{\left(\frac{dx}{dt}\right) ^2+\left(\frac{dy}{dt}\right) ^2} \\
&= e^{at}\sqrt{(a\cos t -\sin t)^2+(a\sin t +\cos t)^2} \\
&= e^{at}\sqrt{a^2(\cos ^2t+\sin ^2t)+(\sin ^2t+\cos ^2t)} \\
&= e^{at}\sqrt{a^2+1}
\end{aligned}\]
である.
よって, $\vec p,$ $\vec v$ のなす角 $\theta$ について
\[\cos\theta = \frac{\vec p\cdot\vec v}{|\vec p||\vec v|} = \frac{ae^{2at}}{e^{at}\cdot e^{at}\sqrt{a^2+1}} = \frac{a}{\sqrt{a^2+1}}\]
は $t$ によらないから, $\theta$ は一定である.

参考
- 曲線 $[*]$ は, 上記の性質から「等角らせん」(equiangular spiral) と呼ばれ, また「対数らせん」(logarithmic spiral), 「ベルヌーイらせん」(Bernoulli spiral) とも呼ばれる.
- 上記の「等角らせん」の性質を応用して, $2$ 枚の刃のなす角が一定になるようなはさみ「フィットカットカーブ」(プラス株式会社) が実用化されている.
加速度
定義《直線・平面・空間における動点の加速度》
$n$ 次元空間において, 動点 $\mathrm P(x_1,\cdots,x_n)$ の座標 $x_1,$ $\cdots,$ $x_n$ が時刻 $t$ の関数として $2$ 回微分可能であるとする.
このとき, 時刻 $t$ における点 $\mathrm P$ の加速度 $\vec\alpha$ を
\[\vec\alpha = \left(\frac{d^2x_1}{dt^2},\cdots,\frac{d^2x_n}{dt^2}\right),\]
加速度の大きさ $|\vec\alpha |$ を
\[ |\vec\alpha | = \sqrt{\left(\frac{d^2x_1}{dt^2}\right) ^2+\cdots +\left(\frac{d^2x_n}{dt^2}\right) ^2}\]
で定める.
問題《斜方投射における物体の加速度》
広い平地において, 速さ $v_0$ で地面から角 $\theta$ をなす方向に投げられた物体の時刻 $t$ における位置 $(x,y)$ は, 空気抵抗がないとき, 定数 $g\,(> 0)$ を用いて
\[ x = v_0\cos\theta\cdot t, \quad y = v_0\sin\theta\cdot t-\frac{1}{2}gt^2\]
と表されるという.
この物体の加速度の大きさを求めよ.
解答例
この物体の加速度ベクトルは, 時刻 $t$ において
\[\left(\frac{d^2x}{dt^2},\frac{d^2y}{dt^2}\right) = (0,-g)\]
である.
よって, 求める加速度の大きさは
\[\sqrt{0^2+(-g)^2} = g\]
である.
問題《等速円運動》
単位円周上を単位時間に角 $\omega$ の割合で回転する動点 $(\cos\omega t,\sin\omega t )$ の時刻 $t$ における速度 $\vec v$ と加速度 $\vec\alpha$ は互いに垂直であることを示せ.
解答例
\[\begin{aligned}
\vec v &= (-\omega\sin\omega t,\omega\cos\omega t), \\
\vec\alpha &= (-\omega ^2\cos\omega t,-\omega ^2\sin\omega t)
\end{aligned}\]
であり,
\[\vec v\cdot\vec\alpha \!=\! (-\omega\sin\omega t)(-\omega ^2\cos\omega t)\!+\!(\omega\cos\omega t)(-\omega ^2\sin\omega t) \!=\! 0\]
であるから, $\vec v\perp\vec\alpha$ である.
問題《放物線に関する面積速度一定の法則》
$xy$ 平面上の放物線 $C:y = x^2$ 上を運動する点 $\mathrm P$ がある.
時刻 $t = 0$ のとき点 $\mathrm P$ は原点 $\mathrm O$ にあるとし, 時刻 $t\,(\geqq 0)$ における $\mathrm P$ の座標を $(x,y)$ とおく.
$C$ の焦点を $\mathrm F$ とおき, 時刻 $t$ における線分 $\mathrm{OF},$ $\mathrm{FP}$ と $C$ の弧 $\mathrm{OP}$ とで囲まれる部分の面積を $S$ とおく.
さらに, $S' = \dfrac{dS}{dt},$ $x' = \dfrac{dx}{dt},$ $x'' = \dfrac{d^2x}{dt^2},$ $y'' = \dfrac{d^2y}{dt^2}$ とおく.
このとき, $t > 0$ において, 常に $S' = 1$ が成り立つとする.
- (1)
- $x,$ $x'$ を用いて $x'',$ $y''$ を表せ.
- (2)
- 点 $\mathrm P$ の加速度ベクトル $\vec\alpha = (x'',y'')$ は $\overrightarrow{\mathrm{PF}}$ に平行であり, かつ $|\vec\alpha |\cdot\mathrm{PF}^2$ は $t$ によらず一定であることを証明せよ.
(参考: 中央大)
解答例
- (1)
- 放物線 $C:y = x^2$ つまり $x^2 = 4\cdot\dfrac{1}{4}\cdot y$ の焦点 $\mathrm F$ の座標は $\left( 0,\dfrac{1}{4}\right)$ である.
よって,
\[ S = \frac{x}{2}\left( x^2+\frac{1}{4}\right) -\int_0^xX^2\,dX = \frac{1}{6}x^3+\frac{1}{8}x\]
から,
\[ S' = \left(\frac{1}{2}x^2+\frac{1}{8}\right)x'\]
である.
仮定 $S' = 1$ から \[ (4x^2+1)x' = 8 \quad \cdots [1]\] であるので, 両辺を $t$ で微分すると \[\begin{aligned} &8x(x')^2+(4x^2+1)x'' = 0 \\ &x'' = -\frac{8x(x')^2}{4x^2+1} \end{aligned}\] が得られる. よって, \[\begin{aligned} y'' &= (x^2)'' = (2xx')' = 2(x')^2+2xx'' \\ &= 2(x')^2-\frac{16x^2(x')^2}{4x^2+1} \end{aligned}\] である.
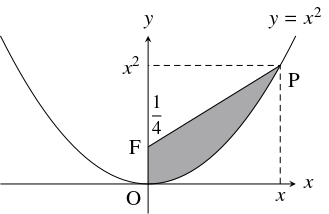
- (2)
- \[\begin{aligned} \overrightarrow{\mathrm{PF}} &= \left( -x,\frac{1}{4}-x^2\right), \quad \cdots [2] \\ |\overrightarrow{\mathrm{PF}}|^2 &= x^2+\left(\frac{1}{4}-x^2\right) ^2 = \left( x^2+\frac{1}{4}\right) ^2 \quad \cdots [3] \end{aligned}\] であるから, \[\begin{aligned} \vec\alpha &= (x'',y'') \\ &= \left( -\frac{8x(x')^2}{4x^2+1},2(x')^2-\frac{16x^2(x')^2}{4x^2+1}\right) \\ &= \frac{8(x')^2}{4x^2+1}\left( -x,\frac{4x^2+1}{4}-2x^2\right) \\ &= \frac{8(x')^2}{4x^2+1}\left( -x,\frac{1}{4}-x^2\right) \\ &= \frac{8^3}{(4x^2+1)^3}\overrightarrow{\mathrm{PF}} \quad (\because [1],\ [2]) \\ &= \frac{8^3}{4^3|\overrightarrow{\mathrm{PF}}|^3}\overrightarrow{\mathrm{PF}} \quad (\because [3]) \\ &= \frac{8}{|\overrightarrow{\mathrm{PF}}|^2}\cdot\frac{\overrightarrow{\mathrm{PF}}}{|\overrightarrow{\mathrm{PF}}|} \end{aligned}\] が成り立つ. よって, $\vec\alpha$ は $\overrightarrow{\mathrm{PF}}$ に平行であり, $|\vec\alpha |\cdot\mathrm{PF}^2 = 8$ (一定) である.
参考
古典天体力学で, 定点 $\mathrm F$ にある物体から万有引力を受けた物体 $\mathrm P$ は, 楕円 (円を含む) の周, 放物線, 双曲線のいずれかの軌道を描くこと (「ケプラーの第一法則」), 動径 $\mathrm{FP}$ が単位時間に通過する範囲の面積は一定であること (「ケプラーの第二法則」または「面積速度一定の法則」) が知られている.
