微分係数・導関数 (理系)
微分係数・導関数
定理《微分の線形性》
関数 $f(x),$ $g(x)$ が $x = a$ で微分可能であるとし, $k$ を定数として, $(kf)(x),$ $(f+g)(x),$ $(f-g)(x)$ を
\[ (kf)(x) = kf(x), \quad (f\pm g)(x) = f(x)\pm g(x)\]
で定まる関数とする.
このとき,
\[ (kf)'(a) = kf'(a), \quad (f\pm g)'(a) = f'(a)\pm g'(a)\]
が成り立つ.
証明
\[\begin{aligned}
&\frac{kf(x)-kf(a)}{x-a} = k\cdot\frac{f(x)-f(a)}{x-a} \\
&\to kf'(a) \quad (x \to a), \\
&\frac{\{ f(x)\pm g(x)\} -\{ f(a)\pm g(a)\}}{x-a} \\
&= \frac{f(x)-f(a)}{x-a}\pm\frac{g(x)-g(a)}{x-a} \\
&\to f'(a)\pm g'(a) \quad (x \to a)
\end{aligned}\]
であるから, 求める等式が成り立つ.
定理《積・商の微分法》
関数 $f(x),$ $g(x)$ が $x = a$ で微分可能であるとし,
$(fg)(x),$ $\left(\dfrac{f}{g}\right) (x)$ を
\[ (fg)(x) = f(x)g(x), \quad \left(\frac{f}{g}\right) (x) = \frac{f(x)}{g(x)}\]
で定まる関数とする.
このとき,
\[\begin{aligned}
(fg)'(a) &= f'(a)g(a)+f(a)g'(a),\\
\left(\frac{f}{g}\right) '(a) &= \frac{f'(a)g(a)-f(a)g'(a)}{g(a)^2}
\end{aligned}\]
が成り立つ.
証明
\[\begin{aligned}
&\frac{f(x)g(x)-f(a)g(a)}{x-a} \\
&= \frac{f(x)-f(a)}{x-a}g(x)+f(a)\frac{g(x)-g(a)}{x-a} \\
&\to f'(a)g(a)+f(a)g'(a) \quad (x \to a)
\end{aligned}\]
であるから, 第 $1$ 式が成り立つ.
また,
\[\begin{aligned}
&\frac{\dfrac{1}{g(x)}-\dfrac{1}{g(a)}}{x-a} = -\frac{1}{g(x)g(a)}\cdot\frac{g(x)-g(a)}{x-a} \\
&\to -\frac{g'(a)}{g(a)^2} \quad (x \to a)
\end{aligned}\]
であるから $\left(\dfrac{1}{g}\right)'(a) = -\dfrac{g'(a)}{g(a)^2}$ が成り立ち, これを第 $1$ 式と組み合わせると
\[\begin{aligned}
&\left(\frac{f}{g}\right) '(a) = \left( f\cdot\dfrac{1}{g}\right) '(a) = f'(a)\left(\frac{1}{g}\right) (a)+f(a)\left(\frac{1}{g}\right) '(a) \\
&= f'(a)\cdot\frac{1}{g(a)}+f(a)\cdot\left\{-\frac{g'(a)}{g(a)^2}\right\} = \frac{f'(a)g(a)-f(a)g'(a)}{g(a)^2}
\end{aligned}\]
が得られる.
定理《合成関数の微分法》
関数 $f(x)$ が $x = a$ で微分可能で, $f(x)$ と合成可能な関数 $g(x)$ が $x = f(a)$ で微分可能であるとき, $h(x) = (g\circ f)(x)$ は $x = a$ で微分可能であり,
\[ h'(a) = g'(f(a))f'(a)\]
が成り立つ.
証明
\[\begin{aligned}
&\frac{h(x)-h(a)}{x-a} = \frac{g(f(x))-g(f(a))}{x-a} \\
&= \frac{g(f(x))-g(f(a))}{f(x)-f(a)}\cdot\frac{f(x)-f(a)}{x-a} \\
&\to g'(f(a))f'(a) \quad (x \to a)
\end{aligned}\]
であるから, $h'(a) = g'(f(a))f'(a)$ が成り立つ.
定理《逆関数の微分法》
関数 $f(x)$ が逆関数 $g(x)$ をもつとする.
$f(x)$ が $x = a$ で微分可能であることと $g(x)$ が $x = f(a)$ で微分可能であることは同値で, そのとき
\[ g'(f(a)) = \dfrac{1}{f'(a)}\]
が成り立つ.
証明
$y = f(x)$ とおくと, $x = g(f(x))$ となるから, 両辺を $x$ で微分すると, 合成関数の微分法により
\[ 1 = g'(f(a))f'(a)\]
つまり $g'(f(a)) = \dfrac{1}{f'(a)}$ が得られる.
定理《媒介変数表示された関数の導関数》
$x$ の関数 $y$ が媒介変数 $t$ を用いて $x = f(t),$ $y = g(t)$ と表されるとき,
\[\frac{dy}{dx} = \frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}} = \frac{g'(t)}{f'(t)}\]
が成り立つ.
証明
合成関数の微分法, 逆関数の微分法により
\[\frac{dy}{dx} = \frac{dy}{dt}\cdot\frac{dt}{dx} = \frac{dy}{dt}\cdot\frac{1}{\dfrac{dx}{dt}}\]
であるから, 求める等式が成り立つ.
定理《三角関数の導関数》
$(\cos x)' = -\sin x,$ $(\sin x)' = \cos x,$ $(\tan x)' = \dfrac{1}{\cos ^2x}$ が成り立つ.
証明
\[\begin{aligned}
&\frac{\cos (x+h)-\cos x}{h} \\
&= \frac{\cos x\cos h-\sin x\sin h-\cos x}{h} \\
&= -\cos x\cdot\frac{1-\cos h}{h}-\sin x\cdot\frac{\sin h}{h} \\
&= -\cos x\cdot\frac{\sin ^2h}{h(1+\cos h)}-\sin x\cdot\frac{\sin h}{h} \\
&= -\cos x\cdot\frac{\sin h}{h}\cdot\frac{\sin h}{1+\cos h}-\sin x\cdot\frac{\sin h}{h} \\
&\to -\cos x\cdot 1\cdot\frac{0}{2}-\sin x\cdot 1 = -\sin x \quad (h \to 0), \\
&\frac{\sin (x+h)-\sin x}{h} \\
&= \frac{\sin x\cos h+\cos x\sin h-\sin x}{h} \\
&= -\sin x\cdot\frac{1-\cos h}{h}+\cos x\cdot\frac{\sin h}{h} \\
&= -\sin x\cdot\frac{\sin ^2h}{h(1+\cos h)}+\cos x\cdot\frac{\sin h}{h} \\
&= -\sin x\cdot\frac{\sin h}{h}\cdot\frac{\sin h}{1+\cos h}+\cos x\cdot\frac{\sin h}{h} \\
&\to -\sin x\cdot 1\cdot\frac{0}{2}+\cos x\cdot 1 = \cos x \quad (h \to 0)
\end{aligned}\]
であるから, $(\cos x)' = -\sin x,$ $(\sin x)' = \cos x$ が成り立つ.
さらに, 商の導関数の公式により
\[\begin{aligned}
(\tan x)' &= \left(\frac{\sin x}{\cos x}\right) ' \\
&= \frac{(\sin x)'\cos x-\sin x(\cos x)'}{\cos ^2x} \\
&= \frac{\cos ^2x+\sin ^2x}{\cos ^2x} \\
&= \frac{1}{\cos ^2x}
\end{aligned}\]
が成り立つ.
別証明
$(\sin x)' = \cos x$ を使うと, $(\cos x)' = -\sin x$ は,
\[ (\cos x)' \!=\! \left\{\sin\left(\frac{\pi}{2}\!-\!x\right)\right\} ' \!=\! \cos\left(\frac{\pi}{2}\!-\!x\right)\!\cdot\!(-1) \!=\! -\sin x\]
と証明できる.
また, 正接の加法定理を使うと, $(\tan x)' = \dfrac{1}{\cos ^2x}$ は, \[\begin{aligned} &\frac{\tan (x+h)-\tan x}{h} \\ &= \frac{1}{h}\left(\frac{\tan x+\tan h}{1-\tan x\tan h}-\tan x\right) \\ &= \frac{1}{h}\cdot\frac{\tan h+\tan ^2x\tan h}{1-\tan x\tan h} \\ &= \frac{\tan h}{h}\cdot\frac{1+\tan ^2x}{1-\tan x\tan h} \\ &= \frac{\sin h}{h}\cdot\frac{1}{\cos h}\cdot\frac{1}{\cos ^2x}\cdot\frac{1}{1-\tan x\tan h} \\ &\to 1\cdot\frac{1}{1}\cdot\frac{1}{\cos ^2x}\cdot\frac{1}{1-0} = \frac{1}{\cos ^2x} \quad (h \to 0) \end{aligned}\] から証明できる.
また, 正接の加法定理を使うと, $(\tan x)' = \dfrac{1}{\cos ^2x}$ は, \[\begin{aligned} &\frac{\tan (x+h)-\tan x}{h} \\ &= \frac{1}{h}\left(\frac{\tan x+\tan h}{1-\tan x\tan h}-\tan x\right) \\ &= \frac{1}{h}\cdot\frac{\tan h+\tan ^2x\tan h}{1-\tan x\tan h} \\ &= \frac{\tan h}{h}\cdot\frac{1+\tan ^2x}{1-\tan x\tan h} \\ &= \frac{\sin h}{h}\cdot\frac{1}{\cos h}\cdot\frac{1}{\cos ^2x}\cdot\frac{1}{1-\tan x\tan h} \\ &\to 1\cdot\frac{1}{1}\cdot\frac{1}{\cos ^2x}\cdot\frac{1}{1-0} = \frac{1}{\cos ^2x} \quad (h \to 0) \end{aligned}\] から証明できる.
定理《指数関数・対数関数の導関数》
\[\begin{aligned}
(e^x)' &= e^x, & (a^x)' &= a^x\log a, \\
\log x &= \frac{1}{x}, & (\log _ax)' &= \frac{1}{x\log a}
\end{aligned}\]
が成り立つ.
証明
底の変換公式により, $(\log _ax)' = \dfrac{1}{x\log a}$ を示すには $(\log x)' = \dfrac{1}{x}$ を示せばよい.
\[\begin{aligned}
&\frac{\log (x+h)-\log x}{h} = \frac{1}{h}\log\frac{x+h}{x} \\
&= \frac{1}{x}\cdot\frac{x}{h}\log\left( 1+\frac{h}{x}\right) = \frac{1}{x}\log\left( 1+\frac{h}{x}\right) ^{\frac{x}{h}} \\
&\to \frac{1}{x}\log e = \frac{1}{x} \quad (h \to 0)
\end{aligned}\]
であるから, $(\log x)' = \dfrac{1}{x}$ が成り立つ.
また, $f(x) = a^x$ とおくと, $\log f(x) = x\log a$ となるので, 両辺を $x$ で微分すると \[\frac{f'(x)}{f(x)} = \log a\] となり, $f'(x) = f(x)\log a = a^x\log a$ が得られる.
また, $f(x) = a^x$ とおくと, $\log f(x) = x\log a$ となるので, 両辺を $x$ で微分すると \[\frac{f'(x)}{f(x)} = \log a\] となり, $f'(x) = f(x)\log a = a^x\log a$ が得られる.
$(e^x)' = e^x$ の別証明: $\lim\limits_{h \to 0}\dfrac{e^h-1}{h} = 1$ を利用
\[\begin{aligned}
\frac{e^{x+h}-e^x}{h} &= e^x\cdot\frac{e^h-1}{h} \\
&\to e^x\cdot 1 = e^x \quad (h \to 0)
\end{aligned}\]
であるから, $(e^x)' = e^x$ が成り立つ.
問題《積・商の微分法》
関数 $f(x),$ $g(x)$ が $x = a$ で微分可能であるとし,
$(fg)(x),$ $\left(\dfrac{f}{g}\right) (x)$ を
\[ (fg)(x) = f(x)g(x), \quad \left(\frac{f}{g}\right) (x) = \frac{f(x)}{g(x)}\]
で定まる関数とする.
このとき,
\[\begin{aligned}
(fg)'(a) &= f'(a)g(a)+f(a)g'(a),\\
\left(\frac{f}{g}\right) '(a) &= \frac{f'(a)g(a)-f(a)g'(a)}{g(a)^2}
\end{aligned}\]
が成り立つことを示せ.
解答例
こちらを参照.
問題《多項式の重根判定法》
$f(x)$ を実数係数多項式, $\alpha$ を実数とする.
- (1)
- $\alpha,$ $f(\alpha ),$ $f'(\alpha )$ を用いて $f(x)$ を $(x-\alpha )^2$ で割った余りを表せ.
- (2)
- $f(x)$ が $(x-\alpha )^2$ で割り切れるための必要十分条件は, $f(\alpha ) = f'(\alpha ) = 0$ であることを示せ.
解答例
- (1)
- $f(x)$ を $(x-\alpha )^2$ で割った商を $q(x),$ 余りを $ax+b$ ($a,$ $b$: 実数) とおく. このとき, \[ f(x) = (x-\alpha )^2q(x)+ax+b \quad \cdots [1]\] が成り立つ. 両辺を $x$ で微分すると \[ f'(x) = 2(x-\alpha )q(x)+(x-\alpha )^2q'(x)+a \quad \cdots [2]\] となる. $[1],$ $[2]$ に $x = \alpha$ を代入すると, \[ f(\alpha ) = a\alpha +b, \quad f'(\alpha ) = a\] となり, $b = f(\alpha )-a\alpha = f(\alpha )-\alpha f'(\alpha )$ となる. ゆえに, 求める余りは, $xf'(\alpha )+f(\alpha )-\alpha f'(\alpha )$ である.
- (2)
- (1) の結果から,
が成り立つ.
$f(x)$ が $(x-\alpha )^2$ で割り切れる $\iff$ $xf'(\alpha )+f(\alpha )-\alpha f'(\alpha ) = 0$ $\iff$ $f'(\alpha ) = f(\alpha )-\alpha f'(\alpha ) = 0$ $\iff$ $f(\alpha ) = f'(\alpha ) = 0$
参考
- 多項式 $f(x)$ について, $f(x) = 0$ の重解を $f(x)$ の「重根」(multiple root) と呼ぶ.
- 一般に, 実数係数多項式 $f(x)$ が $(x-\alpha )^m$ で割り切れるための必要十分条件は, \[ f(\alpha ) = f'(\alpha ) = \cdots = f^{(m-1)}(\alpha ) = 0\] であることが知られている.
- 有理数係数の場合にも, 多項式を関数として微分するには実数の範囲で極限の概念を使わなければならないが, その公式 \[\left(\sum_{k = 0}^na_kx^k\right) ' = \sum_{k = 1}^nka_kx^{k-1}\] を多項式の形式的な微分の定義として採用すれば, 極限の概念を使わずに上記のような議論ができる. また, 複素数係数の場合にも, 同様の議論により, 上記の判定法が証明できる. この形式的な微分をした多項式を「導多項式」(derivative of polynomial) と呼ぶ.
問題《くじで当たらない確率の極限値》
$n$ 本中 $1$ 本だけ当たりが入ったくじを $n$ 回引くときに $1$ 回も当たらない確率 $p_n$ について, 極限値 $\lim\limits_{n \to \infty}p_n$ を求めよ.
ただし, 引いたくじはその都度もとに戻すものとする.
解答例
このくじにおいて, 当たりの確率は $\dfrac{1}{n},$ はずれの確率は $1-\dfrac{1}{n}$ であるから, $n$ 回引くときに $1$ 回も当たらない確率 $p_n$ は
\[ p_n = \left( 1-\frac{1}{n}\right)^n\]
である.
ゆえに, 求める極限値は
\[\lim\limits_{n \to \infty}p_n = \lim\limits_{n \to \infty}\frac{1}{\left( 1+\dfrac{1}{-n}\right)^{-n}} = \frac{1}{e}\]
である.
ここで,
\[ e = \lim\limits_{k \to 0}(1+k)^{\frac{1}{k}} = \lim\limits_{x \to \pm\infty}\left( 1+\frac{1}{x}\right) ^x\]
であることを使った.
問題《ベルヌーイの不等式とネイピア数の評価》
$n$ を $2$ 以上の整数とする.
次のことを示せ.
- (1)
- $(1+x)^n > 1+nx$ $(x > 0)$ が成り立つ.
- (2)
- $\dfrac{{}_n\mathrm C_k}{n^k} \leqq \dfrac{1}{2^{k-1}}$ $(1 \leqq k \leqq n)$ が成り立つ.
- (3)
- $2 \leqq e \leqq 3$ である.
解答例
- (1)
- 二項定理により, $x > 0$ のとき \[ (1+x)^n = 1+nx+\cdots +x^n > 1+nx\] が成り立つ.
- (2)
- ${}_n\mathrm C_k = \dfrac{{}_n\mathrm P_k}{k!}$ であるから, $2^{k-1}{}_n\mathrm P_k \leqq k!n^k$ を示せばよい. これは, \[ 2^{k-1} = 2^{k-1}\cdot 1 \leqq k!, \quad {}_n\mathrm P_k \leqq n^k\] の辺々を掛け合わせることで得られる.
- (3)
- $n \geqq 2$ のとき, (1) の不等式に $x = \dfrac{1}{n}$ を代入すると, \[\left( 1+\frac{1}{n}\right) ^n > 1+n\cdot\frac{1}{n} = 2\] となる. また, 二項定理と (2) の不等式により \[\begin{aligned} \left( 1+\frac{1}{n}\right) ^n &= 1+\sum_{k = 1}^n{}_n\mathrm C_k\left(\frac{1}{n}\right) ^k = 1+\sum_{k = 1}^n\frac{{}_n\mathrm C_k}{n^k} \\ &\leqq 1+\sum_{k = 1}^n\frac{1}{2^{k-1}} = 1+\frac{1-\left(\dfrac{1}{2}\right) ^n}{1-\dfrac{1}{2}} \\ &= 3-\frac{1}{2^{n-1}} < 3 \end{aligned}\] が成り立つ. ゆえに, 挟みうちの原理と $e = \lim\limits_{n \to \infty}\left( 1+\dfrac{1}{n}\right) ^n$ により, \[ 2 \leqq e \leqq 3\] である.
参考
※$2022/06/13$『関数の極限』から移動
問題《コーシーの関数方程式》
- (1)
- 実数全体で定義された実数値関数 $f(x)$ が, すべての実数 $x_1,$ $x_2$ に対して
\[ f(x_1+x_2) = f(x_1)+f(x_2) \quad \cdots [*]\]
を満たすとする.
- ①
- $f(0)$ の値を求めよ.
- ②
- すべての実数 $x$ に対して $f(-x) = -f(x)$ が成り立つことを示せ.
- ③
- $f(x)$ が $x = 0$ で微分可能で $f'(0) = m$ ($m$: 実数) であるとする. このとき, $f(x)$ は実数全体で微分可能であることを示し, $f(x)$ の導関数 $f'(x)$ を求めよ.
- (2)
- 実数全体で定義された実数値関数 $g(x)$ が, すべての実数 $x_1,$ $x_2,$ $x$ に対して \[ g(x_1+x_2) = g(x_1)g(x_2)\] と $g(x) > 0$ を満たし, $x = 0$ で微分可能で $g'(0) = 1$ であるとする. このとき, $g(x)$ とその導関数 $g'(x)$ の関係式を導け.
- (3)
- 正の数全体で定義された実数値関数 $h(X)$ が, すべての正の数 $X_1,$ $X_2$ に対して \[ h(X_1X_2) = h(X_1)+h(X_2)\] を満たし, $X = 1$ で微分可能で $h'(1) = 1$ であるとする. このとき, $h(X)$ の導関数 $h'(X)$ を求めよ.
(参考: $2009$ 東京慈恵会医科大)
解答例
- (1)
- ①
- $[*]$ に $x_1 = x_2 = 0$ を代入すると $f(0) = f(0)+f(0)$ となるから, $f(0) = 0$ である.
- ②
- $[*]$ に $x_1 = x,$ $x_2 = -x$ を代入すると $f(0) = f(x)+f(-x)$ となるから, $f(-x) = -f(x)$ が成り立つ.
- ③
- 実数 $x,$ $h$ $(h \neq 0)$ に対して $f(x+h) = f(x)+f(h)$ であるから, \[\begin{aligned} \frac{f(x+h)-f(x)}{h} &= \frac{f(h)}{h} = \frac{f(0+h)-f(0)}{h} \\ &\to f'(0) = m \quad (h \to 0) \end{aligned}\] が成り立つ. よって, $f(x)$ は実数全体で微分可能であり, $f'(x) = m$ である.
- (2)
- $g(0) = g(0)g(0),$ $g(x) > 0$ であるから, $g(0) = 1$ である.
仮定から, 関数 $f(x) = \log g(x)$ は, すべての実数 $x_1,$ $x_2$ に対して
\[\begin{aligned}
f(x_1+x_2) &= \log g(x_1+x_2) = \log g(x_1)g(x_2) \\
&= \log g(x_1)+\log g(x_2) = f(x_1)+f(x_2)
\end{aligned}\]
を満たす.
さらに, 合成関数の微分法により,
\[ f'(0) = \dfrac{g'(0)}{g(0)} = \dfrac{1}{1} = 1\]
である.
よって, (1) の結果により $f'(x) = 1$ であるから,
が成り立つ.
$\dfrac{g'(x)}{g(x)} = 1$ つまり $g'(x) = g(x)$ - (3)
- 仮定から, 関数 $f(x) = h(e^x)$ は, すべての実数 $x_1,$ $x_2$ に対して
\[\begin{aligned}
f(x_1+x_2) &= h(e^{x_1+x_2}) = h(e^{x_1}e^{x_2}) \\
&= h(e^{x_1})+h(e^{x_2}) = f(x_1)+f(x_2)
\end{aligned}\]
を満たす.
さらに, 合成関数の微分法により,
\[ f'(0) = h'(e^0)\cdot e^0 = h'(1) = 1\]
である.
よって, (1) の結果により $f'(x) = 1$ であり,
が成り立つから, $h'(X) = \dfrac{1}{X}$ である.
$h'(e^x)\cdot e^x = 1$ つまり $h'(e^x) = \dfrac{1}{e^x}$
参考
- $[*]$ のように, 関数を解とする方程式を「関数方程式」(functional equation) と呼ぶ.
- $[*]$ は「コーシーの関数方程式」(Cauchy's functional equation) として知られている. 関数 $f(x) = mx$ はこの方程式と, $1$ 点 $x = a$ における微分係数 $f'(a) = m$ によって定まる. $1$ 点 $x = a$ における微分可能性から実数全体における微分可能性が導かれることに注意したい.
- 指数関数 $g(x) = e^x$ は, 指数法則 \[ g(x_1+x_2) = g(x_1)g(x_2)\] と $g'(0) = 1$ によって定まる関数であると言える. 実際, $g(x) > 0$ のとき, この方程式から導かれる「微分方程式」$g'(x) = g(x)$ により, \[\begin{aligned} \frac{g'(x)}{g(x)} &= x \\ \int_0^x\frac{g'(t)}{g(t)}\,dt &= \int_0^xdt \\ \log g(x) &= x \\ g(x) &= e^x \end{aligned}\] が得られる.
- 対数関数 $h(X) = \log X$ は, 対数法則 \[ h(X_1X_2) = h(X_1)+h(X_2)\] と $h'(1) = 1$ によって定まる関数であると言える.
問題《双曲線関数の関数方程式》
実数全体で定義された関数 $f(x)$ が, すべての実数 $x_1,$ $x_2$ に対して
\[ f(x_1+x_2) = \frac{f(x_1)+f(x_2)}{1+f(x_1)f(x_2)} \quad \cdots [\ast ]\]
を満たし, $x = 0$ で微分可能で $f'(0) = 1$ であるとする.
また,
\[ g(x) = \dfrac{1+f(x)}{1-f(x)}, \quad h(x) = e^{-2x}g(x)\]
とおく.
- (1)
- $f(0)$ の値を求めよ.
- (2)
- $f(x)$ は微分可能であることを示し, $f(x)$ を用いて $f'(x)$ を表せ.
- (3)
- $-1 < f(x) < 1$ であることを示せ.
- (4)
- $g(x)$ を用いて $g'(x)$ を表せ.
- (5)
- $h'(x)$ を求め, $g(x),$ $f(x)$ を求めよ.
(参考: $2015$ 東北大, $2007$ 京都大, $1994$ 明治大)
解答例
- (1)
- $[\ast ]$ に $x_1 = x_2 = 0$ を代入すると
\[ f(0) = \frac{2f(0)}{1+f(0)^2}\]
となるから, 分母を払って整理すると
\[ f(0)\{ f(0)+1\}\{ f(0)-1\} = 0\]
となる.
仮に $f(0) = \pm 1$ とすると, $[\ast ]$ で $x_1 = x,$ $x_2 = 0$ としたときにとなり, $f'(0) = 0 \neq 1$ となってしまう.$f(x) = \dfrac{f(x)\pm 1}{1\pm f(x)} = \pm 1$ (複号同順)
よって, \[ f(0) = 0 \quad \cdots [1]\] である. - (2)
- $h \neq 0$ のとき, \[\begin{aligned} \frac{f(x+h)-f(x)}{h} &= \frac{1}{h}\left\{\frac{f(x)+f(h)}{1+f(x)f(h)}-f(x)\right\} \\ &= \frac{1}{h}\cdot\frac{f(h)\{ 1-f(x)^2\}}{1+f(x)f(h)} \\ &= \frac{f(h)-f(0)}{h}\cdot\frac{1-f(x)^2}{1+f(x)f(h)} \quad (\because [1]) \end{aligned}\] が成り立つ. $f(x)$ は $x = 0$ で微分可能であり, よって $x = 0$ で連続であることに注意すると, $h \to 0$ のとき, この値は \[\begin{aligned} f'(0)\cdot\frac{1-f(x)^2}{1+f(x)f(0)} = 1-f(x)^2 \quad (\because [1]) \end{aligned}\] に収束する. ゆえに, $f(x)$ は微分可能であり, \[ f'(x) = 1-f(x)^2 \quad \cdots [2]\] が成り立つ.
- (3)
- $[\ast ]$ に $x_1 = x_2 = \dfrac{x}{2}$ を代入して $\pm 1$ を掛け, $1$ を加えると \[ 1\pm f(x) = 1\pm\frac{2f\left(\dfrac{x}{2}\right)}{1+f\left(\dfrac{x}{2}\right) ^2} = \frac{\left\{ 1\pm f\left(\dfrac{x}{2}\right)\right\} ^2}{1+f\left(\dfrac{x}{2}\right) ^2} \geqq 0\] (複号同順) となるから, \[ -1 \leqq f(x) \leqq 1\] が成り立つ. $f(x) = \pm 1$ を満たす $x$ の存在を仮定すると, \[ f(0) = f(x-x) = \frac{\pm 1+f(-x)}{1\pm f(-x)} = \pm 1 \neq 0\] (複号同順) という矛盾が生じる. よって, $-1 < f(x) < 1$ である.
- (4)
- $y = f(x)$ とおく. $g(x)$ を微分すると, \[\begin{aligned} g'(x) &= \frac{d}{dy}\left(\frac{1+y}{1-y}\right)\cdot\frac{dy}{dx} \\ &= \frac{1\cdot (1-y)-(1+y)\cdot (-1)}{(1-y)^2}(1-y^2) \quad (\because [2]) \\ &= \frac{2}{(1-y)^2}(1+y)(1-y) \\ &= \frac{2(1+y)}{(1-y)} = 2g(x) \quad \cdots [3] \end{aligned}\] が得られる.
- (5)
- $h(x)$ を微分すると
\[\begin{aligned}
h'(x) &= -2e^{-2x}g(x)+e^{-2x}g'(x) \\
&= e^{-2x}\{ g'(x)-2g(x)\} = 0 \quad (\because [3])
\end{aligned}\]
となるから, $h(x) = C$ ($C$: 実数) である.
よって, $g(x) = Ce^{2x}$ となるから, $x = 0$ を代入すると
\[ C = g(0) = \frac{1+f(0)}{1-f(0)} = 1 \quad (\because [1])\]
となり,
となる.
$g(x) = e^{2x},$ $\dfrac{1+f(x)}{1-f(x)} = e^{2x}$ つまり $f(x) = \dfrac{e^{2x}-1}{e^{2x}+1}$
参考
- $\tanh x = \dfrac{e^{2x}-1}{e^{2x}+1} = \dfrac{e^x-e^{-x}}{e^x+e^{-x}}$ は, $\cosh x = \dfrac{e^x+e^{-x}}{2},$ $\sinh x = \dfrac{e^x-e^{-x}}{2}$ とともに,「双曲線関数」(hyperbolic function) と呼ばれる.
- $f(x) = \tanh x$ は「関数方程式」$[\ast ]$ と $f'(0) = 1$ から定まる.
問題《逆双曲線関数の導関数》
関数
\[ f(x) = \frac{e^x+e^{-x}}{2}, \quad g(x) = \frac{e^x-e^{-x}}{2}, \quad h(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}\]
について,
- (1)
- \[ f(x)^2-g(x)^2 = 1, \quad h(x) = \frac{g(x)}{f(x)}, \quad 1-h(x)^2 = \frac{1}{f(x)^2}\] が成り立つことを示せ.
- (2)
- \[ f'(x) = g(x), \quad g'(x) = f(x), \quad h'(x) = \frac{1}{f(x)^2}\] が成り立つことを示せ.
- (3)
- $f(x)$ $(x > 0),$ $g(x),$ $h(x)$ の逆関数の導関数をそれぞれ求めよ.
解答例
- (1)
- 定義から, \[\begin{aligned} f(x)^2-g(x)^2 &= \frac{e^{2x}\!+\!2\!+\!e^{-2x}}{4}-\frac{e^{2x}\!-\!2\!+\!e^{-2x}}{4} = 1 \quad \cdots [1], \\ h(x) &= \frac{e^x-e^{-x}}{2}\div\frac{e^x+e^{-x}}{2} = \frac{g(x)}{f(x)} \quad \cdots [2] \end{aligned}\] が成り立つ. $[1]$ の両辺を $f(x)^2$ で割ると, $[2]$ により \[ 1-h(x)^2 = \frac{1}{f(x)^2} \quad \cdots [3]\] が得られる.
- (2)
- $(e^x) = e^x,$ $(e^{-x})' = -e^{-x}$ であるから, \[\begin{aligned} f'(x) &= \frac{e^x+(-e^{-x})}{2} = g(x) \quad \cdots [4], \\ g'(x) &= \frac{e^x-(-e^{-x})}{2} = f(x) \quad \cdots [5] \end{aligned}\] が成り立つ. また, $[2]$ と商の導関数の公式により, \[\begin{aligned} h'(x) &= \frac{g'(x)f(x)-g(x)f'(x)}{f(x)^2} \\ &= \frac{f(x)^2-g(x)^2}{f(x)^2} \quad (\because [4],\ [5]) \\ &= \frac{1}{f(x)^2} \quad (\because [1]) \end{aligned}\] が得られる.
- (3)
- $x = f(y)$ $(y > 0)$ とおくと $[4],$ $[1]$ により \[\frac{dx}{dy} = g(y) = \sqrt{f(y)^2-1} = \sqrt{x^2-1}\] となるから, 逆関数の導関数の公式により \[\frac{d}{dx}f^{-1}(x) = \frac{1}{\sqrt{x^2-1}}\] が得られる. $x = g(y)$ とおくと $[5],$ $[1]$ により \[\frac{dx}{dy} = f(y) = \sqrt{g(y)^2+1} = \sqrt{x^2+1}\] となるから, 逆関数の導関数の公式により \[\frac{d}{dx}g^{-1}(x) = \frac{1}{\sqrt{x^2+1}}\] が得られる. $x = h(y)$ とおくと $[6],$ $[3]$ により \[\frac{dx}{dy} = \frac{1}{f(y)^2} = 1-h(y)^2 = 1-x^2\] となるから, 逆関数の導関数の公式により \[\frac{d}{dx}h^{-1}(x) = \frac{1}{1-x^2}\] が得られる.
参考
- 関数 \[\cosh x = \frac{e^x+e^{-x}}{2}, \quad \sinh x = \frac{e^x-e^{-x}}{2}, \quad \tanh x = \frac{e^x-e^{-x}}{e^x+e^{-x}}\] は, 「双曲線関数」(hyperbolic function) と呼ばれる. 三角関数が円周 $x^2+y^2 = 1$ を使って定義されるように,「双曲線関数」は双曲線 $x^2-y^2 = 1$ を使って定義される. これらの関数は, 相互関係, 加法定理, 導関数の公式など, 多くのよく似た性質をもつことが知られている.
- 「双曲線関数」$\cosh x$ $(x \geqq 0),$ $\sinh x,$ $\tanh x$ の逆関数を「逆双曲線関数」(inverse hyperbolic function) と呼び, それぞれ $\mathrm{arcosh}\,x,$ $\mathrm{arsinh}\,x,$ $\mathrm{artanh}\,x$ で表す (接頭辞は arc ではなく ar). \[\begin{aligned} \mathrm{arcosh}\,x &= \log (x+\sqrt{x^2-1}), \\ \mathrm{arsinh}\,x &= \log (x+\sqrt{x^2+1}), \\ \mathrm{artanh}\,x &= \frac{1}{2}\log\frac{1+x}{1-x} \end{aligned}\] である (こちらを参照).
問題《逆三角関数の導関数》
関数
- (A)
- $y = \cos x$ $(0 < x < \pi )$
- (B)
- $y = \sin x$ $\left( -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\right)$
- (C)
- $y = \tan x$ $\left( -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\right)$
解答例
- (A)
- $y = \cos x$ $(0 < x < \pi )$ の逆関数は, \[ x = \cos y \quad (0 < y < \pi )\] で定まる $x$ の関数 $y$ である. 両辺を $x$ で微分すると \[ 1 = -\sin y\cdot\frac{dy}{dx}\] となるから, この範囲で $\sin y > 0$ であることに注意すると, \[\frac{dy}{dx} = -\frac{1}{\sin y} = -\frac{1}{\sqrt{1-\cos ^2y}} = -\frac{1}{\sqrt{1-x^2}}\] が得られる.
- (B)
- $y = \sin x$ $\left( -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\right)$ の逆関数は, \[ x = \sin y \quad \left( -\dfrac{\pi}{2} < y < \dfrac{\pi}{2}\right)\] で定まる $x$ の関数 $y$ である. 両辺を $x$ で微分すると \[ 1 = \cos y\cdot\frac{dy}{dx}\] となるから, この範囲で $\cos y > 0$ であることに注意すると, \[\frac{dy}{dx} = \frac{1}{\cos y} = \frac{1}{\sqrt{1-\sin ^2y}} = \frac{1}{\sqrt{1-x^2}}\] が得られる.
- (C)
- $y = \tan x$ $\left( -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\right)$ の逆関数は, \[ x = \tan y \quad \left( -\dfrac{\pi}{2} < y < \dfrac{\pi}{2}\right)\] で定まる $x$ の関数 $y$ である. 両辺を $x$ で微分すると \[ 1 = \frac{1}{\cos^2 y}\cdot\frac{dy}{dx}\] となるから, \[\frac{dy}{dx} = \cos^2 y = \frac{1}{1+\tan ^2y} = \frac{1}{1+x^2}\] が得られる.
問題《有名な関数を導関数にもつ関数》
- (A)
- $x\log x-x$
- (B)
- $\log\left|\tan\dfrac{x}{2}\right|$
- (C)
- $\log (x+\sqrt{x^2+a^2})$ $(a > 0)$
解答例
- (A)
- 求める導関数は \[\begin{aligned} \frac{d}{dx}(x\log x-x) &= 1\cdot\log x+x\cdot\frac{1}{x}-1\\ &= \log x \end{aligned}\] である.
- (B)
- 合成関数の微分法により, 求める導関数は \[\begin{aligned} \frac{d}{dx}\log\left|\tan\frac{x}{2}\right| &= \frac{1}{\tan\dfrac{x}{2}}\cdot\frac{1}{\cos ^2\dfrac{x}{2}}\cdot\frac{1}{2} \\ &= \frac{1}{2\sin\dfrac{x}{2}\cos\dfrac{x}{2}} = \frac{1}{\sin x} \end{aligned}\] である.
- (C)
- 合成関数の微分法により, 求める導関数は \[\begin{aligned} &\frac{d}{dx}\log (x+\sqrt{x^2+a^2}) \\ &= \frac{1}{x+\sqrt{x^2+a^2}}\cdot\left( 1+\frac{2x}{2\sqrt{x^2+a^2}}\right) \\ &= \frac{1}{x+\sqrt{x^2+a^2}}\cdot\frac{\sqrt{x^2+a^2}+x}{\sqrt{x^2+a^2}} = \frac{1}{\sqrt{x^2+a^2}} \end{aligned}\] である.
高階導関数
問題《多項式関数のマクローリン展開》
実数値関数 $f(x)$ に対して, $f(x)$ の $0$ 階導関数 $f^{(0)}(x)$ を $f(x)$ と定める.
- (1)
- $n,$ $r$ を非負整数とする. $x^n$ の $r$ 階導関数を求めよ.
- (2)
- $f(x) = \displaystyle\sum_{k = 0}^na_kx^k$ ($a_k$: 実数) のとき, $f(x)$ は \[ f(x) = \sum_{k = 0}^n\frac{f^{(k)}(0)}{k!}x^k\] の形に表されることを示せ.
解答例
- (1)
- (i)
- $r \leqq n$ のとき. \[\begin{aligned} (x^n)^{(r)} &= (nx^{n-1})^{(r-1)} = \cdots \\ &= ({}_n\mathrm P_k\,x^{n-k})^{(r-k)} \\ &= \{ {}_n\mathrm P_k\,(n-k)x^{n-k-1}\} ^{(r-k-1)} \\ &= ({}_n\mathrm P_{k+1}\,x^{n-k-1})^{(r-k-1)} = \cdots \\ &= {}_n\mathrm P_r\,x^{n-r} \end{aligned}\] が成り立つ.
- (ii)
- $r > n$ のとき. (i) から $(x^n)^{(n)} = n!$ であるので, $(x^n)^{(r)} = 0$ である.
- (2)
- $0 \leqq k \leqq n$ なる各整数 $k$ に対して, (1) と微分の線形性により \[ f^{(k)}(x) = a_n\,{}_n\mathrm P_k\,x^{n-k}+\cdots +a_{k+1}\,{}_{k+1}\mathrm P_k\,x+a_k\,k!\] であるから, \[ f^{(k)}(0) = a_k\,k!, \quad a_k = \frac{f^{(k)}(0)}{k!}\] が成り立つ. ゆえに, $f(x)$ は \[ f(x) = \sum_{k = 0}^n\frac{f^{(k)}(0)}{k!}x^k\] と表される.
問題《三角関数と対数関数の高階導関数》
$n$ を正の整数, $a$ を $1$ でない正の数とする.
- (A)
- \[\begin{aligned} \frac{d^n}{dx^n}\cos x &= \cos\left( x+\frac{n\pi}{2}\right) \quad \cdots [\mathrm C], \\ \frac{d^n}{dx^n}\sin x &= \sin\left( x+\frac{n\pi}{2}\right) \quad \cdots [\mathrm S] \end{aligned}\]
- (B)
- \[\frac{d^n}{dx^n}\log _ax = \frac{(-1)^{n-1}(n-1)!}{x^n\log a} \quad \cdots [\mathrm L]\]
解答例
- (A)
- (i)
- 三角関数の導関数の公式 (こちらを参照) により \[\begin{aligned} \frac{d}{dx}\cos x &= -\sin x = \cos\left( x+\frac{\pi}{2}\right), \\ \frac{d}{dx}\sin x &= \cos x = \sin\left( x+\frac{\pi}{2}\right) \end{aligned}\] であるから, $n = 1$ のとき $[\mathrm C],$ $[\mathrm S]$ が成り立つ.
- (ii)
- $n = k$ ($k$: 正の整数) のとき $[\mathrm C],$ $[\mathrm S]$ が成り立つとする. このとき, \[\begin{aligned} &\frac{d^{k+1}}{dx^{k+1}}\cos x = \frac{d}{dx}\left(\frac{d^k}{dx^k}\cos x\right) \\ &= \frac{d}{dx}\cos\left( x+\frac{k\pi}{2}\right) = -\sin\left( x+\frac{k\pi}{2}\right) \\ &= \cos\left( x+\frac{k\pi}{2}+\frac{\pi}{2}\right) = \cos\left( x+\frac{(k+1)\pi}{2}\right), \\ &\frac{d^{k+1}}{dx^{k+1}}\sin x = \frac{d}{dx}\left(\frac{d^k}{dx^k}\sin x\right) \\ &= \frac{d}{dx}\sin\left( x+\frac{k\pi}{2}\right) = \cos\left( x+\frac{k\pi}{2}\right) \\ &= \sin\left( x+\frac{k\pi}{2}+\frac{\pi}{2}\right) = \sin\left( x+\frac{(k+1)\pi}{2}\right) \end{aligned}\] となり, $n = k+1$ のとき $[\mathrm C],$ $[\mathrm S]$ が成り立つ.
- (B)
- (i)
- $y = \log _ax$ のとき $x = a^y$ であるから \[\frac{dy}{dx} = \frac{1}{\dfrac{dx}{dy}} = \frac{1}{a^y\log a} = \frac{1}{x\log a}\] であり, $n = 1$ のとき $[\mathrm L]$ が成り立つ.
- (ii)
- $n = k$ ($k$: 正の整数) のとき $[\mathrm L]$ が成り立つとする. このとき, \[\begin{aligned} &\frac{d^{k+1}}{dx^{k+1}}\log _ax = \frac{d}{dx}\left(\frac{d^k}{dx^k}\log _ax\right) \\ &= \frac{d}{dx}\frac{(-1)^{k-1}(k-1)!}{x^k\log a} = \frac{(-1)^{k-1}(k-1)!}{\log a}\frac{d^k}{dx^k}x^{-k} \\ &= \frac{(-1)^{k-1}(k-1)!}{\log a}\cdot (-k)x^{-k-1} = \frac{(-1)^kk!}{x^{k+1}\log a} \end{aligned}\] となり, $n = k+1$ のとき $[\mathrm L]$ が成り立つ.
問題《三角関数の微分方程式》
実数全体で微分可能な実数値関数 $f(x)$ がすべての実数 $x,$ $x_1,$ $x_2$ に対して
\[\begin{aligned}
&f(-x) = -f(x) \quad \cdots [1], \\
&f'(x_1+x_2) = f'(x_1)f'(x_2)-f(x_1)f(x_2) \quad \cdots [2], \\
&f'(0) = 1 \quad \cdots [3]
\end{aligned}\]
を満たすとする.
- (1)
- $f(0)$ の値を求めよ.
- (2)
- $f'(x)$ は偶関数であることを示せ.
- (3)
- \[ f'(A)-f'(B) = -2f\left(\frac{A+B}{2}\right)f\left(\frac{A-B}{2}\right) \quad \cdots [4]\] が成り立つことを示せ.
- (4)
- $f(x)$ は $2$ 回微分可能であり, \[ f''(x) = -f(x) \quad \cdots [5]\] が成り立つことを示せ.
- (5)
- \[ f(x)^2+f'(x)^2 = 1 \quad \cdots [6] \] が成り立つことを示せ.
(参考: $2020$ 鳥取大)
解答例
- (1)
- $[1]$ に $x = 0$ を代入すると, \[ f(-0) = -f(0)\] よって $f(0) = -f(0),$ $2f(0) = 0$ から \[ f(0) = 0 \quad \cdots [0]\] が得られる.
- (2)
- $[1]$ の両辺を微分すると \[\begin{aligned} f'(-x)\cdot (-1) &= -f'(x) \\ f'(-x) &= f'(x) \quad \cdots [1]' \end{aligned}\] となるから, $f'(x)$ は偶関数である.
- (3)
- $[2]$ において $x_2$ を $-x_2$ に置き換えると, $[1],$ $[1]'$ から \[\begin{aligned} f'(x_1-x_2) &= f'(x_1)f'(-x_2)-f(x_1)f(-x_2) \\ &= f'(x_1)f'(x_2)+f(x_1)f(x_2) \quad \cdots [2]' \end{aligned}\] が得られる. よって, $[2]-[2]'$ から, \[ f'(x_1+x_2)-f'(x_1-x_2) = -2f(x_1)f(x_2)\] が成り立つ. ここで, $A = x_1+x_2,$ $B = x_1-x_2$ とおくと, $x_1 = \dfrac{A+B}{2},$ $x_2 = \dfrac{A-B}{2}$ から \[ f'(A)-f'(B) = -2f\left(\frac{A+B}{2}\right)f\left(\frac{A-B}{2}\right) \quad \cdots [4]\] が得られる.
- (4)
- $[4],$ $[0],$ $[3]$ により \[\begin{aligned} &\frac{f'(x+h)-f'(x)}{h} = \frac{1}{h}\left\{ -2f\left( x+\frac{h}{2}\right) f\left(\frac{h}{2}\right)\right\} \quad (\because [4]) \\ &= -f\left( x+\frac{h}{2}\right)\cdot\frac{2}{h}\left\{ f\left( 0+\frac{h}{2}\right) -f(0)\right\} \quad (\because [0]) \\ &\to -f(x)f'(0) \quad (h \to 0) \\ &= -f(x) \quad (\because [3]) \end{aligned}\] であるから, $f(x)$ は $2$ 回微分可能であり, \[ f''(x) = -f(x) \quad \cdots [5]\] が成り立つ.
- (5)
- $g(x) = f(x)^2+f'(x)^2$ とおく. \[\begin{aligned} g'(x) &= 2f(x)f'(x)+2f'(x)f''(x) \\ &= 2f'(x)\{ f(x)+f''(x)\} \\ &= 2f'(x)\cdot 0 = 0 \quad (\because [5]) \end{aligned}\] であるから, $g(x)$ は定数関数である. $[0],$ $[3]$ により \[ g(0) = f(0)^2+f'(0)^2 = 0^2+1^2 = 1\] であるから, $g(x) = 1$ つまり \[ f(x)^2+f'(x)^2 = 1 \quad \cdots [6]\] が成り立つ.
参考
「微分方程式」の解の一意性により, $\cos x,$ $\sin x$ は, それぞれ初期条件 $f(0)-1 = f'(0) = 0,$ $f(0) = f'(0)-1 = 0$ のもとで,「微分方程式」$f''(x) = -f(x)$ の解として定まる.
$(\sin x)' = \cos x$ であるから, $[2]$ は余弦の加法定理を表す.
問題《高階導関数に関するライプニッツの公式》
$n$ を正の整数として, $u = u(x),$ $v = v(x)$ を $n$ 回微分可能な関数とする.
関数 $uv = u(x)v(x)$ について,
\[ (uv)^{(n)} = \sum\limits_{k = 0}^n{}_n\mathrm C_k\,u^{(n-k)}v^{(k)} \quad \cdots [\ast ]\]
を示せ.
ただし, $u^{(0)} = u,$ $v^{(0)} = v$ と定める.
積の導関数の公式と「パスカルの法則」
\[ {}_n\mathrm C_k+{}_n\mathrm C_{k+1} = {}_{n+1}\mathrm C_{k+1} \quad (0 \leqq k < n)\]
(こちらを参照) は証明なしで使ってよい.
(参考: $2022$ 福島県立医科大, $2020$ 大分大)
解答例
- (i)
- $n = 1$ のとき. 積の導関数の公式 \[ (uv)' = u'v+uv' \quad \cdots [1]\] により, $[*]$ が成り立つ.
- (ii)
- $n = m$ ($m$: 正の整数) のとき $[\ast ]$ が成り立つとして, $u,$ $v$ が $m+1$ 回微分可能であるとする. このとき, $[\ast ]$ の両辺を微分することにより \[\begin{aligned} &(uv)^{(m+1)} = \sum\limits_{k = 0}^m{}_m\mathrm C_k\,\{ u^{(m-k)}v^{(k)}\} ' \\ &= \sum\limits_{k = 0}^m{}_m\mathrm C_k\,\{ u^{(m+1-k)}v^{(k)}+u^{(m-k)}v^{(k+1)}\} \quad (\because [1]) \\ &= \sum\limits_{k = 0}^m{}_m\mathrm C_k\,u^{(m+1-k)}v^{(k)}+\sum\limits_{k = 0}^m{}_m\mathrm C_k\,u^{(m-k)}v^{(k+1)} \\ &= \sum\limits_{k = 0}^m{}_m\mathrm C_k\,u^{(m+1-k)}v^{(k)}+\sum\limits_{k = 1}^{m+1}{}_m\mathrm C_{k-1}\,u^{(m+1-k)}v^{(k)} \\ &= u^{(m+1)}v+\sum\limits_{k = 1}^m({}_m\mathrm C_k+{}_m\mathrm C_{k-1})u^{(m+1-k)}v^{(k)}+uv^{(m+1)} \\ &= \sum\limits_{k = 0}^{m+1}{}_{m+1}\mathrm C_k\,u^{(m+1-k)}v^{(k)} \end{aligned}\] となり, $n = m+1$ のとき $[\ast ]$ が成り立つ. 最後の等号では「パスカルの法則」を使った.
参考
本問で示した等式は, 高階導関数に関する「ライプニッツの公式」(general Leibniz rule) として知られている.
対数微分法
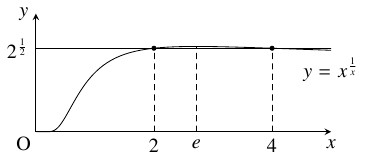
問題《微分積分学におけるシュタイナーの問題》
解答例
- (1)
- $y > 0$ に注意して両辺の対数をとると, \[\log y = \frac{1}{x}\log x\] となる. 両辺を $x$ で微分すると \[\frac{y'}{y} = -\frac{1}{x^2}\cdot\log x+\frac{1}{x}\cdot\frac{1}{x} = \frac{1-\log x}{x^2}\] となるから, \[ y' = y\cdot\frac{1-\log x}{x^2} = x^{\frac{1}{x}-2}(1-\log x)\] である. $x^{\frac{1}{x}-2} > 0$ から \[\begin{aligned} y' \geqq 0 &\iff 1-\log x \geqq 0 \iff 0 < x \leqq e, \\ y' \leqq 0 &\iff x \geqq e \end{aligned}\] であるので, $y$ は $x = e$ で極大かつ最大の値 $e^{\frac{1}{e}}$ をとる.
- (2)
- 整数 $m,$ $n$ が
\[ m^n = n^m \quad \cdots [1], \quad 0 < m < n \quad \cdots [2]\]
を満たすとする.
$[1]$ は
\[ m^{\frac{1}{m}} = n^{\frac{1}{n}}\]
と変形できる.
よって, (1) で見た $y = x^{\frac{1}{x}}$ の増減と $2 < e < 3$ から, $m = 1,$ $2$ が必要である.
$1^n = n^1$ の解は $n = 1$ に限るから, $m = 1$ は不適である.
したがって,
\[ x^{\frac{1}{x}} = 2^{\frac{1}{2}}\]
の正の整数解 $x\,(\neq 2)$ を求めればよい.
曲線 $y = x^{\frac{1}{x}}$ と直線 $y = 2^{\frac{1}{2}}$ はちょうど $2$ 点で交わるから,
$x^{\frac{1}{x}} = 2^{\frac{1}{2}}$ つまり $2^x = x^2$ は $x = 2$ 以外にただ $1$ つの実数解をもつ.
一方, $2^4 = 4^2 = 16$ であるから, それは $x = 4$ である. ゆえに, 求める整数解は $(m,n) = (2,4)$ である.
参考
- (1) は, 微積分における「シュタイナーの問題」(Steiner's calculus problem) として知られている.
- 関数 $y = \dfrac{\log x}{x}$ $(x > 0)$ の最大値も (1) と同様の方法で求められ (各自確認せよ), それを使って (2) を解くこともできる (参考: $2022$ 名古屋市立大).
