定積分の漸化式
定積分の漸化式
問題《ウォリスの公式》
各非負整数 $n$ に対して
\[ I_n = \int_0^{\frac{\pi}{2}}\cos ^nx\,dx\]
とおき,
\[ 0!! = 1, \quad 1!! = 1, \quad n!! = n\cdot (n-2)!! \quad (n \geqq 2)\]
と定める.
次のことを示せ.
- (1)
- \[ I_n = \displaystyle\int_0^{\frac{\pi}{2}}\sin ^nx\,dx\] である.
- (2)
- \[ I_n = \dfrac{n-1}{n}I_{n-2} \quad (n \geqq 2)\] が成り立つ.
- (3)
- \[ I_n = \begin{cases} \dfrac{(n-1)!!}{n!!} & (n\text{: 奇数}), \\ \dfrac{(n-1)!!}{n!!}\cdot\dfrac{\pi}{2} & (n\text{: 偶数}) \end{cases} \quad (n \geqq 1)\] である.
- (4)
- \[ I_{2n} < I_{2n-1}\] が成り立つ.
- (5)
- \[\frac{{}_{2n}\mathrm C_n}{2^{2n}} < \dfrac{1}{\sqrt{\pi n}}\] が成り立つ.
(参考: $2024$ 中央大, $2021$ 岩手大, $2016$ 信州大ほか)
解答例
- (1)
- $t = \dfrac{\pi}{2}-x$ とおくと, $x = \dfrac{\pi}{2}-t,$ $\dfrac{dx}{dt} = -1$ となり, \[\begin{aligned} I_n &= \int_{\frac{\pi}{2}}^0\cos ^n\left(\frac{\pi}{2}-t\right)(-1)\,dt \\ &= \int_0^{\frac{\pi}{2}}\sin ^nx\,dx \quad \cdots [1] \end{aligned}\] となる.
- (2)
- 部分積分法により
\[\begin{aligned}
I_n &= \int_0^{\frac{\pi}{2}}\cos ^{n-1}x\cos x\,dx \\
&= \int_0^{\frac{\pi}{2}}\cos ^{n-1}x(\sin x)'\,dx \\
&= \big[\cos ^{n-1}x\sin x\big] _0^{\frac{\pi}{2}} \\
&\qquad -\int_0^{\frac{\pi}{2}}(n-1)\cos ^{n-2}x(-\sin x)\sin x\,dx \\
&= (n-1)\int_0^{\frac{\pi}{2}}\cos ^{n-2}x(1-\cos ^2x)\,dx \\
&= (n-1)\!\int_0^{\frac{\pi}{2}}\!\cos ^{n-2}x\,dx-(n-1)\!\int_0^{\frac{\pi}{2}}\!\cos ^nx\,dx \\
&= (n-1)I_{n-2}-(n-1)I_n
\end{aligned}\]
と変形できるから,
が成り立つ.
$nI_n = (n-1)I_{n-2}$ つまり $I_n = \dfrac{n-1}{n}I_{n-2} \quad \cdots [2]$ - (3)
- 定義から \[\begin{aligned} I_0 &= \int_0^{\frac{\pi}{2}}\,dx = \big[ x\big] _0^{\frac{\pi}{2}} = \frac{\pi}{2}, \\ I_1 &= \int_0^{\frac{\pi}{2}}\cos x\,dx = \big[\sin x\big] _0^{\frac{\pi}{2}} = 1 \end{aligned}\] であるので, $[2]$ から \[ I_n = \begin{cases} \dfrac{(n-1)!!}{n!!} & (n\text{: 奇数}), \\ \dfrac{(n-1)!!}{n!!}\cdot\dfrac{\pi}{2} & (n\text{: 偶数}) \end{cases} \quad \cdots [3]\] が得られる.
- (4)
- $0 \leqq x \leqq \dfrac{\pi}{2}$ において $0 \leqq \sin x \leqq 1$ から $\sin ^{2n}x \leqq \sin ^{2n-1}x$ であり, 等号成立は $x = 0,$ $\dfrac{\pi}{2}$ の場合に限るので, \[\int_0^{\frac{\pi}{2}}\sin ^{2n}x\,dx < \int_0^{\frac{\pi}{2}}\sin ^{2n-1}x\,dx\] つまり \[ I_{2n} < I_{2n-1} \quad \cdots [4] \quad (\because [1])\] が成り立つ.
- (5)
- $[3],$ $[4]$ から
\[\frac{(2n-1)!!}{(2n)!!}\cdot\frac{\pi}{2} < \frac{(2n-2)!!}{(2n-1)!!}\]
が成り立つので, 両辺を $\dfrac{(2n-1)!!}{(2n)!!}$ で割ると
\[\begin{aligned}
\frac{\pi}{2} &< \frac{(2n-2)!!(2n)!!}{\{ (2n-1)!!\} ^2} \\
&= \frac{1}{2n}\left\{\frac{(2n)!!}{(2n-1)!!}\right\} ^2 \\
&= \frac{1}{2n}\left\{\frac{(2n)!!}{(2n-1)!!}\cdot\frac{(2n)!!}{(2n)!!}\right\} ^2 \\
&= \frac{1}{2n}\left\{\frac{2^nn!\cdot 2^nn!}{(2n)!}\right\} ^2 \\
&= \frac{1}{2n}\left(\frac{2^{2n}}{{}_{2n}\mathrm C_n}\right) ^2
\end{aligned}\]
が得られる.
よって,
が成り立つ.
$n\pi < \left(\dfrac{2^{2n}}{{}_{2n}\mathrm C_n}\right) ^2,$ $\sqrt{n\pi} < \dfrac{2^{2n}}{{}_{2n}\mathrm C_n}$ つまり $\dfrac{{}_{2n}\mathrm C_n}{2^{2n}} < \dfrac{1}{\sqrt{\pi n}}$
参考
- (3) の等式は「ウォリスの公式」(Wallis formula) と呼ばれる.
- (5) の不等式は「ランダム・ウォーク」(random walk) の問題を解く際に使われる (こちらを参照).
- (5) と同様にして, $I_{2n-1} < I_{2n-2}$ から \[\frac{1}{2n}\left(\frac{2^{2n}}{{}_{2n}\mathrm C_n}\right) ^2 < \frac{\pi}{2}\cdot\frac{2n}{2n-1}\] も得られるので, 挟みうちの原理により \[\lim\limits_{n \to \infty}\frac{1}{2n}\left(\frac{2^{2n}}{{}_{2n}\mathrm C_n}\right) ^2 = \frac{\pi}{2}\] が成り立つ. これも「ウォリスの公式」と呼ばれる.
- 「ウォリスの公式」から「スターリングの公式」(Stirling's formula) などの多くの重要な定理が導かれる.
問題《精密版スターリングの公式》
各正の整数 $n$ に対して $a_n = \dfrac{n!}{\sqrt nn^ne^{-n}},$ $b_n = \dfrac{2^{2n}(n!)^2}{\sqrt n(2n)!},$ 各非負整数 $n$ に対して $I_n = \displaystyle\int_0^{\frac{\pi}{2}}\sin ^nx\,dx$ とおき, $0!! = 1,$ $1!! = 1,$ $n!! = n\cdot (n-2)!!$ $(n \geqq 2)$ と定める.
$n \geqq 1$ のとき,「ウォリスの公式」
\[ I_n = \begin{cases}
\dfrac{(n-1)!!}{n!!} & (n\text{: 奇数}), \\
\dfrac{(n-1)!!}{n!!}\cdot\dfrac{\pi}{2} & (n\text{: 偶数})
\end{cases}\]
(こちらを参照), 不等式 $I_{2n+1} < I_{2n} < I_{2n-1}$ が成り立つことを使って, 次のことを示せ.
- (1)
- $\lim\limits_{n \to \infty}b_n = \sqrt\pi$ である.
- (2)
- $0 < \log\dfrac{a_n}{a_{n+1}} < \dfrac{1}{n(n+1)}$ が成り立つ.
- (3)
- $\lim\limits_{n \to \infty}\dfrac{a_n}{a_{2n}} = 1$ である.
- (4)
- $\lim\limits_{n \to \infty}a_n = \sqrt{2\pi}$ である (ヒント: $\dfrac{a_n{}^2}{a_{2n}} = \sqrt 2b_n$).
(参考: $2015$ 大阪大)
解答例
- (1)
- 「ウォリスの公式」により,
\[\begin{aligned}
I_{2n} &= \frac{(2n-1)!!}{(2n)!!}\cdot\frac{\pi}{2} = \frac{(2n)!}{\{ 2n(2n-2)\cdots 2\} ^2}\cdot\frac{\pi}{2} \\
&= \frac{(2n)!}{2^{2n}(n!)^2}\cdot\frac{\pi}{2} = \frac{\pi}{2\sqrt n}\cdot\frac{1}{b_n} \\
I_{2n-1} &= \frac{(2n-2)!!}{(2n-1)!!} = \frac{2n\{ (2n-2)(2n-4)\cdots 2\} ^2}{(2n)!} \\
&= \frac{2^{2n}(n!)^2}{2n\cdot (2n)!} = \frac{1}{2\sqrt n}b_n \\
I_{2n+1} &= \frac{2n}{2n+1}I_{2n-1} = \frac{2n}{2\sqrt n(2n+1)}b_n
\end{aligned}\]
が成り立つ.
これらを $I_{2n+1} < I_{2n} < I_{2n-1}$ に代入すると
\[\frac{2n}{2\sqrt n(2n+1)}b_n < \frac{\pi}{2\sqrt n}\cdot\frac{1}{b_n} < \frac{1}{2\sqrt n}b_n\]
となるから, 両辺の逆数をとると
が得られる. $b_n > 0$ から \[\sqrt\pi < b_n < \sqrt{\left( 1+\frac{1}{2n}\right)\pi}\] であり, 右辺は $\sqrt\pi$ に収束するから, $\lim\limits_{n \to \infty}b_n = \sqrt\pi$ である.
$\dfrac{1}{b_n} < \dfrac{b_n}{\pi} < \dfrac{2n+1}{2n}\cdot\dfrac{1}{b_n}$ つまり $\pi < b_n{}^2 < \left( 1+\dfrac{1}{2n}\right)\pi$ - (2)
- 数列 $\{ a_n\}$ の定義から,
\[\begin{aligned}
\frac{a_n}{a_{n+1}} &= \frac{n!}{\sqrt nn^ne^{-n}}\cdot\frac{\sqrt{n+1}(n+1)^{n+1}e^{-(n+1)}}{(n+1)!} \\
&= \left(\frac{n+1}{n}\right) ^{n+\frac{1}{2}}e^{-1} \\
\log\frac{a_n}{a_{n+1}} &= \left( n+\frac{1}{2}\right)\{\log (n+1)-\log n\} -1
\end{aligned}\]
が成り立つ.
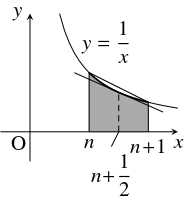
$\log (n+1)-\log n$ は, 曲線 $y = \dfrac{1}{x}$ と $x$ 軸, 直線 $x = n,$ $x = n+1$ が囲む図形の面積を表す.
これは, $x = n+\dfrac{1}{2}$ における $y = \dfrac{1}{x}$ の接線と $x$ 軸, 直線 $x = n,$ $x = n+1$ が囲む図形の面積より大きく,
$2$ 点 $\left( n,\dfrac{1}{n}\right),$ $\left( n+1,\dfrac{1}{n+1}\right)$ を結ぶ直線と $x$ 軸, 直線 $x = n,$ $x = n+1$ が囲む図形の面積より小さいから,
\[\frac{1}{n+\dfrac{1}{2}} < \int_n^{n+1}\frac{dx}{x} < \frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right)\]
が成り立つ.
よって, \[\begin{aligned} 0 < \log\frac{a_n}{a_{n+1}} &< \left( n+\frac{1}{2}\right)\cdot\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right) -1 = \frac{1}{4n(n+1)} \\ 0 < \log\frac{a_n}{a_{n+1}} &< \frac{1}{n(n+1)} \end{aligned}\] が成り立つ.
- (3)
- (2) の不等式から, 各正の整数 $k$ に対して
\[ 0 < \log a_k-\log a_{k+1} < \frac{1}{k}-\frac{1}{k+1}\]
が成り立つ.
$n \leqq k \leqq 2n-1$ なるすべての整数 $k$ に対して辺々を加えると,
が成り立つ. 右辺は $e^0 = 1$ に収束するから, 挟みうちの原理により $\lim\limits_{n \to \infty}\dfrac{a_n}{a_{2n}} = 1$ である.
$0 < \log a_n-\log a_{2n} < \dfrac{1}{n}-\dfrac{1}{2n},$ $0 < \log\dfrac{a_n}{a_{2n}} < \dfrac{1}{2n}$ つまり $1 < \dfrac{a_n}{a_{2n}} < e^{\frac{1}{2n}}$ - (4)
- 数列 $\{ a_n\}$ の定義から \[\begin{aligned} \frac{a_n{}^2}{a_{2n}} &= \frac{(n!)^2}{n\cdot n^{2n}e^{-2n}}\cdot\frac{\sqrt{2n}(2n)^{2n}e^{-2n}}{(2n)!} \\ &= \sqrt 2\cdot\frac{2^{2n}(n!)^2}{\sqrt n(2n)!} = \sqrt 2b_n \end{aligned}\] が成り立つので, (1), (3) から \[\begin{aligned} a_n &= \sqrt 2b_n\left(\frac{a_n}{a_{2n}}\right) ^{-1} \\ &\to \sqrt 2\cdot\sqrt \pi\cdot 1^{-1} = \sqrt{2\pi} \quad (n \to \infty ) \end{aligned}\] が得られる.
参考
- (4) は「スターリングの公式」(Stirling's formula) と呼ばれ, 二項分布が正規分布で近似できるという「ド・モアブル=ラプラスの定理」(de Moivre–Laplace theorem) の証明で使われる.
- (2) のように定積分の値を台形の面積で近似する方法を「台形近似」と呼ぶ.
問題《バーゼル問題》
各非負整数 $n$ に対して
\[ I_n = \int_0^{\frac{\pi}{2}}\cos ^nx\,dx, \quad J_n = \int_0^{\frac{\pi}{2}}x^2\cos ^{2n}x\,dx\]
とおき,
\[ 0!! = 1, \quad 1!! = 1, \quad n!! = n\cdot (n-2)!! \quad (n \geqq 2)\]
と定める.
「ウォリスの公式」
\[ I_n = \begin{cases}
\dfrac{(n-1)!!}{n!!} & \!\!(n\text{: 奇数}), \\
\dfrac{(n-1)!!}{n!!}\cdot\dfrac{\pi}{2} & \!\!(n\text{: 偶数})
\end{cases} \quad (n \geqq 1)\]
(こちらを参照) を使って, 次のことを示せ.
ただし, (3) において, $0 \leqq x \leqq \dfrac{\pi}{2}$ のとき $x \leqq \dfrac{\pi}{2}\sin x$ であること (こちらを参照) は証明なしに使ってよい.
- (1)
- $n \geqq 1$ のとき, \[ J_n = \frac{2n-1}{2n}J_{n-1}-\frac{1}{2n^2}I_{2n} \quad \cdots [1]\] が成り立つ.
- (2)
- $n \geqq 1$ のとき, \[ J_n = \frac{(2n-1)!!}{(2n)!!}\cdot\frac{\pi}{4}\left(\frac{\pi ^2}{6}-\sum_{k = 1}^n\frac{1}{k^2}\right) \quad \cdots [2]\] である.
- (3)
- $n \geqq 1$ のとき, \[ J_n \leqq \frac{1}{2n+2}\cdot\frac{(2n-1)!!}{(2n)!!}\left(\frac{\pi}{2}\right) ^3 \quad \cdots [3]\] が成り立つ.
- (4)
- \[\sum_{n = 1}^\infty\frac{1}{n^2} = \frac{\pi ^2}{6} \quad \cdots [4]\] である.
(参考: $2003$ 日本女子大)
解答例
- (1)
- 部分積分法により \[\begin{aligned} J_n &= \int_0^{\frac{\pi}{2}}x^2\cos ^{2n-1}x\cos x\,dx \\ &= \int_0^{\frac{\pi}{2}}x^2\cos ^{2n-1}x(\sin x)'\,dx \\ &= \left[x^2\cos ^{2n-1}x\sin x\right] _0^{\frac{\pi}{2}} \\ &\qquad -\int_0^{\frac{\pi}{2}}\{ 2x\cos ^{2n-1}x \\ &\qquad +(2n-1)x^2\cos ^{2n-2}x(-\sin x)\}\sin x\,dx \\ &= \frac{1}{n}\int_0^{\frac{\pi}{2}}x\cdot 2n\cos ^{2n-1}x(-\sin x)\,dx \\ &\qquad +(2n-1)\int_0^{\frac{\pi}{2}}x^2\cos ^{2n-2}x\sin ^2x\,dx \\ &= \frac{1}{n}\int_0^{\frac{\pi}{2}}x(\cos ^{2n}x)'\,dx \\ &\qquad +(2n-1)\int_0^{\frac{\pi}{2}}x^2\cos ^{2n-2}x(1-\cos ^2x)\,dx \\ &= \frac{1}{n}\left[ x\cos ^{2n}x\right] _0^{\frac{\pi}{2}} -\frac{1}{n}\int_0^{\frac{\pi}{2}}\cos ^{2n}x\,dx \\ &\qquad +(2n-1)\int_0^{\frac{\pi}{2}}x^2\cos ^{2n-2}x\,dx \\ &\qquad -(2n-1)\int_0^{\frac{\pi}{2}}x^2\cos ^{2n}x\,dx \\ &= -\frac{1}{n}I_{2n}+(2n-1)J_{n-1}-(2n-1)J_n \end{aligned}\] と変形できるから, \[ J_n = \frac{2n-1}{2n}J_{n-1}-\frac{1}{2n^2}I_{2n} \quad \cdots [1]\] が得られる.
- (2)
- 数学的帰納法で示す.
- (i)
- $n = 1$ のとき. $[1]$ と「ウォリスの公式」により, \[\begin{aligned} J_1 &= \frac{1}{2}J_0-\frac{1}{2}I_2 = \frac{1}{2}\left[\frac{x^3}{3}\right] _0^{\frac{\pi}{2}}-\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{\pi}{2} \\ &= \frac{1}{2}\left(\frac{\pi ^3}{24}-\frac{\pi}{4}\right) = \frac{1!!}{2!!}\cdot\frac{\pi}{4}\left(\frac{\pi ^2}{6}-\frac{1}{1^2}\right) \end{aligned}\] であるから, $[2]$ が成り立つ.
- (ii)
- $n = m-1$ ($m$: $1$ より大きい整数) のとき $[2]$ が成り立つとする. このとき, $[1]$ と「ウォリスの公式」により \[\begin{aligned} J_m &= \frac{2m-1}{2m}J_{m-1}-\frac{1}{2m^2}I_{2m} \\ &= \frac{2m-1}{2m}\cdot\frac{(2m-3)!!}{(2m-2)!!}\cdot\frac{\pi}{4}\left(\frac{\pi ^2}{6}-\sum_{k = 1}^{m-1}\frac{1}{k^2}\right) \\ &\qquad -\frac{1}{2m^2}\cdot\frac{(2m\!-\!1)!!}{(2m)!!}\cdot\frac{\pi}{2} \\ &= \frac{(2m-1)!!}{(2m)!!}\cdot\frac{\pi}{4}\left(\frac{\pi ^2}{6}-\sum_{k = 1}^{m-1}\frac{1}{k^2}-\frac{1}{m^2}\right) \\ &= \frac{(2m-1)!!}{(2m)!!}\cdot\frac{\pi}{4}\left(\frac{\pi ^2}{6}-\sum_{k = 1}^m\frac{1}{k^2}\right) \end{aligned}\] となり, $n = m$ のとき $[2]$ が成り立つ.
- (3)
- $0 \leqq x \leqq \dfrac{\pi}{2}$ において $x \leqq \dfrac{\pi}{2}\sin x$ から
であるので, 積分の単調性により \[\begin{aligned} J_n &\leqq \frac{\pi ^2}{4}\int_0^{\frac{\pi}{2}}\sin ^2x\cos ^{2n}x\,dx \\ &= \frac{\pi ^2}{4}\int_0^{\frac{\pi}{2}}(1-\cos ^2x)\cos ^{2n}x\,dx \\ &= \frac{\pi ^2}{4}\left(\int_0^{\frac{\pi}{2}}\cos ^{2n}x\,dx-\int_0^{\frac{\pi}{2}}\cos ^{2n+2}x\,dx\right) \\ &= \frac{\pi ^2}{4}(I_{2n}-I_{2n+2}) \\ &= \frac{\pi ^2}{4}\left\{\frac{(2n-1)!!}{(2n)!!}\cdot\frac{\pi}{2}-\frac{(2n+1)!!}{(2n+2)!!}\cdot\frac{\pi}{2}\right\}\\ &= \left( 1-\frac{2n+1}{2n+2}\right)\frac{(2n-1)!!}{(2n)!!}\left(\frac{\pi}{2}\right) ^3 \\ &= \frac{1}{2n+2}\cdot\frac{(2n-1)!!}{(2n)!!}\left(\frac{\pi}{2}\right) ^3 \quad \cdots [3] \end{aligned}\] が得られる.
$x^2 \leqq \dfrac{\pi ^2}{4}\sin ^2x$ よって $x^2\cos ^{2n}x \leqq \dfrac{\pi ^2}{4}\sin ^2x\cos ^{2n}x$ - (4)
- $[2],$ $[3]$ から
\[\begin{aligned}
0 &\leqq \frac{(2n-1)!!}{(2n)!!}\cdot\frac{\pi}{4}\left(\frac{\pi ^2}{6}-\sum_{k = 1}^n\frac{1}{k^2}\right) \\
&\leqq \frac{1}{2n+2}\cdot\frac{(2n-1)!!}{(2n)!!}\left(\frac{\pi}{2}\right) ^3
\end{aligned}\]
が成り立つので, 各辺を $\dfrac{(2n-1)!!}{(2n)!!}\cdot\dfrac{\pi}{4}\,(> 0)$ で割ると
\[ 0 \leqq \frac{\pi ^2}{6}-\sum_{k = 1}^n\frac{1}{k^2} \leqq \frac{1}{2n+2}\cdot\frac{\pi ^2}{2}\]
が得られる.
右辺は $0$ に収束するから, 挟みうちの原理により
が得られる.
$\displaystyle\lim\limits_{n \to \infty}\left(\frac{\pi ^2}{6}-\sum_{k = 1}^n\frac{1}{k^2}\right) = 0$ つまり $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^2} = \frac{\pi ^2}{6} \quad \cdots [4]$
参考
- 「調和級数」$\displaystyle\sum_{n = 1}^\infty\frac{1}{n}$ は発散するが, 平方数の逆数の無限和 $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^2}$ は収束する. この証明は比較的容易であり, \[\begin{aligned} 0 &< \sum_{k = 1}^n\frac{1}{k^2} = 1+\sum_{k = 2}^n\frac{1}{k^2} \\ &< 1+\sum_{k = 2}^n\frac{1}{(k-1)k} = 1+\sum_{k = 2}^n\left(\frac{1}{k-1}-\frac{1}{k}\right) \\ &= 2-\frac{1}{n} \end{aligned}\] の右辺が収束することからわかる. しかし, $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^2}$ の値を決定する問題はかなり難しい. この問題は, 初期の研究を行ったベルヌーイ兄弟と解決に成功したオイラーの故郷の名前を冠して「バーゼル問題」と呼ばれている.
- $2$ 個の整数が互いに素である確率が $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^2}$ に等しいことも, オイラーによって明らかにされた.
- オイラーはこの問題を一般化して, 偶数 $s$ に対して「汎調和級数」$\displaystyle\sum\limits_{n = 1}^\infty\frac{1}{n^s}$ の値を表す公式を得た. これは「リーマン・ゼータ関数」の定式化につながる重要な発見であった.
- 不等式 $\dfrac{2}{\pi}x \leqq \sin x \leqq x$ $\left( 0 \leqq x \leqq \dfrac{\pi}{2}\right)$ は「ジョルダンの不等式」(Jordan's inequality) と呼ばれる (こちらを参照).
問題《ネイピア数の無理性》
各正の整数 $n$ に対して, $f_n(x) = x^ne^{1-x}$ とおき, $I_n = \displaystyle\int_0^1f_n(x)\,dx$ とおく.
- (1)
- $0 \leqq f_n(x) \leqq 1$ $(0 \leqq x \leqq 1)$ と $0 < I_n < 1$ を示せ.
- (2)
- $I_1$ の値を求めよ. また, $I_n$ を用いて $I_{n+1}$ を表せ.
- (3)
- \[\frac{I_n}{n!} = e-\sum_{k = 0}^n\frac{1}{k!} \quad \cdots [\ast ]\] を数学的帰納法で示せ.
- (4)
- $n!e$ は整数でなく, $e$ は無理数であることを示せ.
- (5)
- $0 < I_n < \dfrac{e}{n+1}$ を示し, 無限級数 $\displaystyle\sum_{n = 1}^\infty\frac{1}{n!}$ の和を求めよ.
(参考: $2019$ 中央大, $1997$ 大阪大, $1988$ 新潟大ほか)
解答例
- (1)
- $f_n(x)$ を微分すると, \[ f_n{}'(x) = nx^{n-1}e^{1-x}+x^n(-e^{1-x}) = x^{n-1}(n-x)e^{1-x}\] となる. よって, $0 < x < 1$ において, $f_n{}'(x) > 0$ が成り立つから, $f(x)$ は単調増加である. これと $f_n(x)$ の連続性により \[ 0 = f_n(0) \leqq f_n(x) \leqq f_n(1) = 1 \quad (0 \leqq x \leqq 1)\] であり, 等号成立は $x = 0,$ $1$ の場合に限る. ゆえに, 積分の単調性により, \[\int_0^10\,dx < \int_0^1f_n(x)\,dx < \int_0^11\,dx\] つまり $0 < I_n < 1$ が成り立つ.
- (2)
- 定義から, \[\begin{aligned} I_1 &= \int_0^1x(-e^{1-x})'\,dx = \big[ -xe^{1-x}\big] _0^1+\int_0^1e^{1-x}\,dx \\ &= -1-\big[ e^{1-x}\big] _0^1 = e-2 \end{aligned}\] であり, \[\begin{aligned} I_{n+1} &= \int_0^1x^{n+1}(-e^{1-x})'\,dx \\ &= \big[ -x^{n+1}e^{1-x}\big] _0^1+\int_0^1(n+1)x^ne^{1-x}\,dx \\ &= (n+1)I_n-1 \end{aligned}\] が成り立つ.
- (3)
- (i)
- $n = 1$ のとき. $\dfrac{I_1}{1!} = e-\dfrac{1}{0!}-\dfrac{1}{1!}$ から, $[\ast ]$ が成り立つ.
- (ii)
- $n = m$ ($m$: 正の整数) のとき $[\ast ]$ が成り立つとする. このとき, (2) の結果から \[\begin{aligned} &\frac{I_{m+1}}{(m+1)!} = \frac{(m+1)I_m-1}{(m+1)!} = \frac{I_m}{m!}-\frac{1}{(m+1)!} \\ &= e-\sum_{k = 0}^m\frac{1}{k!}-\frac{1}{(m+1)!} = e-\sum_{k = 0}^{m+1}\frac{1}{k!} \end{aligned}\] となり, $n = m+1$ のとき $[\ast ]$ が成り立つ.
- (4)
- $[*]$ により, \[ I_n = n!e-n!\sum_{k = 0}^n\frac{1}{k!}\] が成り立つ. (1) で示した $0 < I_n < 1$ から, この値は整数でない. 一方, $n!\displaystyle\sum_{k = 0}^n\frac{1}{k!}$ は整数であるから, $n!e$ は整数でない. よって, $e$ は無理数である. 実際, $e$ が有理数であるとすれば, $e$ は正の整数の比として表され, その分母の絶対値 $n$ について $n!e$ が整数となってしまうからである.
- (5)
- $0 < x < 1$ において $e^{-x} < 1$ であるから, 積分の単調性により \[ 0 < I_n = e\int_0^1x^ne^{-x}\,dx < e\int_0^1x^n\,dx = e\left[\frac{x^{n+1}}{n+1}\right] _0^1 = \frac{e}{n+1}\] が成り立つ. これと $[*]$ により \[ 0 < \frac{I_n}{n!} = e-\sum_{k = 0}^n\frac{1}{k!} < \frac{e}{(n+1)!}\] が成り立つから, 挟みうちの原理により求める無限級数は収束してその和は \[\sum_{n = 0}^\infty\frac{1}{n!} = e\] であることがわかる.
参考
ネイピア数 $e$ の無理性は, $18$ 世紀半ばにオイラーによって証明された.
問題《円周率の無理性》
各非負整数 $n$ に対して
\[ I_n = \frac{\pi^{n+1}}{n!}\int_0^1t^n(1-t)^n\sin\pi t\,dt\]
とおく.
- (1)
- $x \geqq 0$ において \[\sum_{k = 0}^n\frac{x^k}{k!} \leqq e^x \quad \cdots [\text A]\] であることを示せ.
- (2)
- $a \geqq 0$ とする. $[\text A]$ を使って, \[\sum_{k = 0}^na^kI_k \leqq \pi e^{a\pi} \quad \cdots [\text B]\] を示せ.
- (3)
- $I_0,$ $I_1$ の値を求め, \[ I_{n+2} = \frac{4n+6}{\pi}I_{n+1}-I_n \quad \cdots [\text C]\] を示せ.
- (4)
- $\pi$ が無理数であるという定理を示したい. $\pi$ が正の整数 $a,$ $b$ を用いて $\pi = \dfrac{a}{b}$ と表されるとする. このとき, $a^nI_n$ は整数であることを示せ. さらに, これから矛盾を導くことで, 定理を示せ.
(参考: $2003$ 大阪大)
解答例
- (1)
- 各非負整数 $n$ に対して,
\[ f_n(x) = e^x-\left( 1+\frac{x}{1!}+\cdots +\frac{x^n}{n!}\right) \quad (x \geqq 0)\]
とおく.
$f_n(x) \geqq 0$ を示せばよい.
- (i)
- $n = 0$ のとき. $x \geqq 0$ において, $e^x \geqq 1$ であるから, $f_n(x) = f_0(x) = e^x-1 \geqq 0$ である.
- (ii)
- $n = m$ ($m$: 非負整数) のとき $f_n(x) \geqq 0$ であるとする. このとき, $x > 0$ において \[\begin{aligned} f_{m+1}{}'(x) &= e^x-\left\{ 0+\frac{1}{1!}+\frac{2x}{2!}+\cdots +\frac{(m+1)x^m}{(m+1)!}\right\} \\ &= f_m(x) \geqq 0 \end{aligned}\] であり, $x = 0$ において $f_{m+1}(x)$ は連続であるから, $f_{m+1}(x) \geqq f_{m+1}(0) = 0$ となる. よって, $n = m+1$ のとき $f_n(x) \geqq 0$ が成り立つ.
- (2)
- $0 \leqq t \leqq 1$ のとき $t^n(1-t)^n\sin\pi t \leqq 1$ であるから, 積分の単調性により, \[\begin{aligned} \sum_{k = 0}^na^kI_k &= \sum_{k = 0}^na^k\frac{\pi ^{k+1}}{k!}\int_0^1t^k(1-t)^k\sin\pi t\,dt \\ &\leqq \sum_{k = 0}^na^k\frac{\pi ^{k+1}}{k!} = \pi\sum_{k = 0}^n\frac{(a\pi )^k}{k!} \\ &\leqq \pi e^{a\pi} \quad \cdots [\text B] \quad (\because [\text A]) \end{aligned}\] が成り立つ.
- (3)
- $I_0,$ $I_1$ の値は, \[\begin{aligned} I_0 &= \pi\int_0^1\sin\pi t\,dt = \pi\left[\frac{-\cos\pi t}{\pi}\right] _0^1 = 2, \\ I_1 &= \pi ^2\int_0^1t(1-t)\sin\pi t\,dt \\ &= \pi ^2\left\{\left[ t(1-t)\frac{-\cos\pi t}{\pi}\right] _0^1-\int_0^1(1-2t)\frac{-\cos\pi t}{\pi}\,dt\right\} \\ &= \pi\int_0^1(1-2t)\cos\pi t\,dt \\ &= \pi\left\{\left[ (1-2t)\frac{\sin\pi t}{\pi}\right] _0^1-\int_0^1(-2)\cdot\frac{\sin\pi t}{\pi}\,dt\right\} \\ &= 2\int_0^1\sin\pi t\,dt = \frac{4}{\pi} \end{aligned}\] である. また, \[\frac{d}{dt}t^k(1-t)^k = kt^{k-1}(1-t)^{k-1}(1-2t)\] であるから, \[\begin{aligned} I_{n+2} &= \frac{\pi ^{n+3}}{(n+2)!}\int_0^1t^{n+2}(1-t)^{n+2}\sin\pi t\,dt \\ &= \frac{\pi ^{n+3}}{(n+2)!}\left\{\left[ t^{n+2}(1-t)^{n+2}\frac{-\cos\pi t}{\pi}\right] _0^1\right. \\ &\qquad \left.+\int_0^1(n+2)t^{n+1}(1-t)^{n+1}(1-2t)\frac{\cos\pi t}{\pi}\,dt\right\} \\ &= \frac{\pi ^{n+2}}{(n+1)!}\int_0^1t^{n+1}(1-t)^{n+1}(1-2t)\cos\pi t\,dt \end{aligned}\] が成り立つ. ここで, \[\begin{aligned} &\frac{d}{dt}t^{n+1}(1-t)^{n+1}(1-2t) \\ &= (n+1)t^n(1-t)^n(1-2t)^2+t^{n+1}(1-t)^{n+1}(-2) \\ &= (n+1)t^n(1-t)^n-(4n+6)t^{n+1}(1-t)^{n+1} \end{aligned}\] であるから, \[\begin{aligned} I_{n+2} &= \frac{\pi ^{n+2}}{(n+1)!}\left\{\left[ t^{n+1}(1-t)^{n+1}(1-2t)\frac{\sin\pi t}{\pi}\right] _0^1\right. \\ &\qquad -\int_0^1(n+1)t^n(1-t)^n\frac{\sin\pi t}{\pi}\,dt \\ &\qquad \left.+\int_0^1(4n+6)t^{n+1}(1-t)^{n+1}\frac{\sin\pi t}{\pi}\,dt\right\} \\ &= \frac{4n+6}{\pi}I_{n+1}-I_n \quad \cdots [\text C] \end{aligned}\] が成り立つ.
- (4)
- $\pi = \dfrac{a}{b}$ ($a,$ $b$: 正の整数) を $[\text C]$ に代入すると, \[ I_{n+2} = \frac{(4n+6)b}{a}I_{n+1}-I_n\] つまり \[ a^{n+2}I_{n+2} = (4n+6)b(a^{n+1}I_{n+1})-a^2(a^nI_n)\] となる. $a^0I_0 = 2,$ $a^1I_1 = 4b$ は整数であり, $I_n > 0$ であるから, すべての非負整数 $n$ に対して $a^nI_n$ は正の整数である. $[\text B]$ において, 左辺の極限は無限個の正の整数の和で $\infty$ に発散するのに対し, 右辺は $n$ の値によらず一定である. これは矛盾であるから, 定理が成り立つ.
参考
- 円周率 $\pi$ の無理性は, ドイツの数学者 J・H・ランベルトによって初めて証明された ($1761$ 年). 現在では, さまざまな証明がある. 本問は, $20$ 世紀半ばに発見された初等的な証明に基づいている.
- $\pi$ は無理数であるだけでなく, どのような有理数係数多項式 $f(x)$ に対しても $f(x) = 0$ の解にならないことが知られている. このような複素数は「超越数」(transcendental number) と呼ばれる.
