区分求積法
区分求積法
定理《区分求積法》
区間 $a \leqq x \leqq b$ で連続な関数 $f(x)$ に対して,
\[\begin{aligned}
\int_a^b f(x)\,dx &= \lim_{n \to \infty}\frac{b-a}{n}\sum_{k = 0}^{n-1}f\left( a+k\cdot\frac{b-a}{n}\right) \\
&= \lim_{n \to \infty}\frac{b-a}{n}\sum_{k = 1}^nf\left( a+k\cdot\frac{b-a}{n}\right)
\end{aligned}\]
が成り立つ.
問題《メルカトル級数とその項の並べ替え》
- (1)
- $\displaystyle\sum_{k = 1}^{2n}\frac{(-1)^{k-1}}{k} = \sum_{k = 1}^n\frac{1}{n+k}$ を示せ.
- (2)
- 無限級数 $\displaystyle\sum_{n = 1}^\infty\frac{(-1)^{n-1}}{n}$ の和を求めよ.
- (3)
- 項を並べ替えた無限級数 $\displaystyle\sum_{n = 1}^\infty\left(\frac{1}{2n-1}-\frac{1}{4n-2}-\frac{1}{4n}\right)$ の和を求めよ.
(参考: $2024$ 浜松医科大, $2019$ 埼玉大)
解答例
- (1)
- 左辺を変形すると, \[\begin{aligned} &\sum_{k = 1}^{2n}\frac{(-1)^{k-1}}{k} \\ &= \sum_{k = 1}^n\frac{1}{2k-1}-\sum_{k = 1}^n\frac{1}{2k}+2\sum_{k = 1}^n\frac{1}{2k}-2\sum_{k = 1}^n\frac{1}{2k} \\ &= \sum_{k = 1}^n\frac{1}{2k-1}+\sum_{k = 1}^n\frac{1}{2k}-\sum_{k = 1}^n\frac{1}{k} \\ &= \sum_{k = 1}^{2n}\frac{1}{k}-\sum_{k = 1}^n\frac{1}{k} = \sum_{k = 1}^n\frac{1}{n+k} \quad \cdots [1] \end{aligned}\] となる.
- (2)
- $[1]$ から, \[\begin{aligned} &\sum_{n = 1}^\infty\frac{(-1)^{n-1}}{n} = \lim_{n \to \infty}\sum_{k = 1}^n\frac{(-1)^{k-1}}{k} \\ &= \lim_{n \to \infty}\sum_{k = 1}^{2n}\frac{(-1)^{k-1}}{k} = \lim_{n \to \infty}\sum_{k = 1}^{n}\frac{1}{n+k} \\ &= \lim_{n \to \infty}\frac{1}{n}\sum_{k = 1}^{n}\frac{1}{1+\dfrac{k}{n}} = \int_0^1\frac{dx}{1+x} \\ &= \big[\log (1+x)\big] _0^1 = \log 2 \quad \cdots [2] \end{aligned}\] である.
- (3)
- $[2]$ から, \[\begin{aligned} &\sum_{n = 1}^\infty\left(\frac{1}{2n-1}-\frac{1}{4n-2}-\frac{1}{4n}\right) \\ &= \sum_{n = 1}^\infty\left(\frac{1}{4n-2}-\frac{1}{4n}\right) \\ &= \frac{1}{2}\sum_{n = 1}^\infty\left(\frac{1}{2n-1}-\frac{1}{2n}\right) \\ &= \frac{1}{2}\sum_{n = 1}^\infty\frac{(-1)^{n-1}}{n} = \frac{1}{2}\log 2 \end{aligned}\] が得られる.
参考
- 自然対数関数は \[\log (1+x) = \sum_{n = 1}^\infty\frac{(-1)^{n-1}x^n}{n} \quad (-1 < x \leqq 1)\] と「テイラー展開」される (こちらを参照). (2) の無限級数は, ここで $x = 1$ として得られるものであり,「メルカトル級数」(Mercator series) と呼ばれる. このように項の符号が交互に変わる無限級数を「交代級数」(alternative series) と呼ぶ.
- 「正項級数」(positive series) と呼ばれる各項が非負の無限級数と違って,「交代級数」では項を並べ替えると値の変化することがある.
- $\displaystyle\sum_{n = 1}^\infty\frac{1}{2n-1}$ から $p$ 項, $-\displaystyle\sum_{n = 1}^\infty\frac{1}{2n}$ から $q$ 項を交互にとって得られる無限級数の和は $\log 2+\dfrac{1}{2}\log\dfrac{p}{q}$ に等しいことが知られている.
問題《正方形と内接円上にある格子点の個数の比》
$n$ を正の整数とする.
\[ x^2+y^2 \leqq n^2\]
を満たす整数の組 $(x,y)$ の個数を $a_n$ とおき,
\[ |x| \leqq n, \quad |y| \leqq n\]
を満たす整数の組 $(x,y)$ の個数を $b_n$ とおく.
- (1)
- 極限 $L = \lim\limits_{n \to \infty}\dfrac{a_n}{b_n}$ の値を求めよ.
- (2)
- $\dfrac{a_n}{b_n} < \dfrac{\pi}{4}$ を示せ.
(参考: $2009$ 山梨大)
解答例
- (1)
- $x^2+y^2 \leqq n^2$ を満たす正の整数の組 $(x,y)$ の個数は $\displaystyle\sum_{k = 1}^n[\sqrt{n^2-k^2}]$ ($[x]$: $x$ 以下の最大の整数) であるから,
\[ a_n = 1+4n+4\sum_{k = 1}^n[\sqrt{n^2-k^2}]\]
が成り立つ.
また, $b_n = (2n+1)^2$ であり,
\[\frac{4n+1}{(2n+1)^2} = \frac{\dfrac{4}{n}+\dfrac{1}{n^2}}{\left( 2+\dfrac{1}{n}\right) ^2} \to 0 \quad (n \to \infty )\]
であるから,
\[ L = \lim_{n \to \infty}\frac{a_n}{b_n} = \lim_{n \to \infty}\frac{4}{(2n+1)^2}\sum_{k = 1}^n[\sqrt{n^2-k^2}]\]
である.
\[ c_n = \dfrac{4}{(2n+1)^2}\sum_{k =1}^n\sqrt{n^2-k^2}\]
とおくと,
\[\sqrt{n^2-k^2}-1 < [\sqrt{n^2-k^2}] \leqq \sqrt{n^2-k^2}\]
から
\[\begin{aligned}
c_n-\frac{4n}{(2n+1)^2} < \frac{4}{(2n+1)^2}\sum_{k =1}^n[\sqrt{n^2-k^2}] \leqq c_n
\end{aligned}\]
となり,
\[\begin{aligned}
&c_n = \frac{4}{\left( 2+\dfrac{1}{n}\right) ^2}\cdot\frac{1}{n}\sum_{k = 1}^n\sqrt{1-\left(\frac{k}{n}\right) ^2} \\
&\quad \to \int_0^1\sqrt{1-x^2}\,dx = \frac{\pi}{4} \quad (n \to \infty ), \\
&\frac{4n}{(2n+1)^2} = \frac{\dfrac{4}{n}}{\left( 2+\dfrac{1}{n}\right) ^2} \to 0 \quad (n \to \infty )
\end{aligned}\]
となるから, 挟みうちの原理により $L = \dfrac{\pi}{4}$ である.
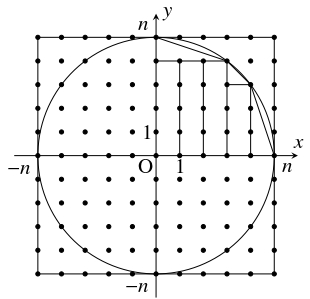
- (2)
- $n+1$ 個の点 $(k,[\sqrt{n^2-k^2}])$ $(0 \leqq k \leqq n)$ のうち $y$ 座標の異なる点と原点を順に結んでできる多角形, 半径 $n$ の四分円の面積を比較すると \[\sum_{k = 1}^n[\sqrt{n^2-k^2}] +\frac{n}{2} \leqq \frac{\pi n^2}{4}\] となるから, \[ a_n \leqq (4n+1)+(\pi n^2-2n) = \pi n^2+2n+1\] が得られる. よって, \[\begin{aligned} \frac{\pi}{4}-\frac{a_n}{b_n} &\geqq \frac{\pi}{4}-\frac{\pi n^2+2n+1}{(2n+1)^2} \\ &= \pi\left\{\frac{1}{4}-\frac{n^2}{(2n+1)^2}\right\} -\frac{1}{2n+1} \\ &= \frac{\pi (4n+1)}{4(2n+1)^2}-\frac{1}{2n+1} \\ &= \frac{4n(\pi -3)+4(n-1)+\pi}{4(2n+1)^2} > 0 \end{aligned}\] から, $\dfrac{a_n}{b_n} < \dfrac{\pi}{4}$ が成り立つ.
参考
- 円上にある「格子点」の個数を求める問題は「ガウスの円問題」として知られている.
- 半径 $n$ の円の面積は $\pi n^2,$ 正方形 $|x| \leqq n,$ $|y| \leqq n$ の面積は $4n^2$ であるから, 本問の結果により, 円上にある「格子点」の個数は, 半径が大きくなるにつれて, 円の面積に近づいていくことがわかる.
