微分方程式 (高校発展)
微分方程式
$y' = y$ のように, 導関数を含み, 関数を解とする方程式を「微分方程式」(differential equation) と呼ぶ.
問題《指数関数の微分方程式》
実数全体で微分可能であり, 正の数全体を値域とする実数値関数 $f(x)$ が
\[ f'(x) = f(x), \quad f(0) = 1\]
を満たすとする.
このとき, $f'(x) = f(x) > 0$ であるから, $f(x)$ の逆関数 $g(x)$ が存在する.
- (1)
- $g'(x)$ を求めて, $g(x) = \displaystyle\int_1^x\dfrac{dt}{t}$ であることを示せ.
- (2)
- すべての正の数 $x_1,$ $x_2$ に対して $g(x_1x_2) = g(x_1)+g(x_2)$ が成り立つことを示せ.
- (3)
- すべての実数 $x_1,$ $x_2$ に対して $f(x_1+x_2) = f(x_1)f(x_2)$ が成り立つことを示せ.
- (4)
- $g'(1)$ の値から $f(1) = \lim\limits_{n \to \infty}\left( 1+\dfrac{1}{n}\right) ^{n}$ であることを示せ.
解答例
- (1)
- $y = f(x)$ とおくと, 逆関数の微分法と仮定により \[\frac{dx}{dy} = \frac{1}{y'} = \frac{1}{y}\] となるから, \[ g'(x) = \dfrac{1}{x} \quad \cdots [1]\] である. また, $f(0) = 1$ から \[ g(1) = 0 \quad \cdots [2]\] であるので, \[ g(x) = g(x)-g(1) = \int_1^x\frac{dt}{t} \quad \cdots [3]\] が成り立つ.
- (2)
- $[3]$ から, すべての正の数 $x_1,$ $x_2$ に対して \[\begin{aligned} g(x_1x_2) &= \int_1^{x_1x_2}\frac{dt}{t} = \int_1^{x_1}\frac{dt}{t}+\int_{x_1}^{x_1x_2}\frac{dt}{t} \\ &= g(x_1)+\int_1^{x_2}\frac{1}{x_1u}x_1\,du \quad (t = x_1u\text{ と置換}) \\ &= g(x_1)+g(x_2) \quad \cdots [4] \end{aligned}\] が成り立つ.
- (3)
- 実数 $x_1,$ $x_2$ に対して $y_1 = f(x_1),$ $y_2 = f(x_2)$ とおくと, $g(y_1) = x_1,$ $g(y_2) = x_2$ となるので, $[4]$ から, \[\begin{aligned} f(x_1+x_2) &= f(g(y_1)+g(y_2)) = f(g(y_1y_2)) \quad (\because [4]) \\ &= y_1y_2 = f(x_1)f(x_2) \end{aligned}\] が得られる.
- (4)
- $[1],$ $[2]$ から, \[ 1 = g'(1) = \lim\limits_{h \to 0}\frac{g(1+h)-g(1)}{h} = \lim\limits_{h \to 0}\frac{1}{h}g(1+h)\] が成り立つ. よって, \[\begin{aligned} 1 &= \lim\limits_{n \to \infty}ng\left( 1+\frac{1}{n}\right) \quad \left(\because n \to \infty\text{ のとき }\frac{1}{n} \to 0\right) \\ &= \lim\limits_{n \to \infty}g\left(\left( 1+\frac{1}{n}\right) ^n\right) \quad (\because [4]) \\ &= g\left(\lim\limits_{n \to \infty}\left( 1+\frac{1}{n}\right) ^n\right) \quad (\because g(x)\text{ は連続}) \end{aligned}\] であるから, $f(1) = \lim\limits_{n \to \infty}\left( 1+\dfrac{1}{n}\right) ^n$ が成り立つ.
参考
- $f'(x) = f(x)$ のように, 導関数を含む「関数方程式」(関数を解とする方程式) を「微分方程式」(differential equation) と呼ぶ. 「微分方程式」は現代解析学で非常に重要な役割を果たす.
- 指数関数 $f(x) = e^x$ は,「微分方程式」 \[ f'(x) = f(x), \quad f(0) = 1 \quad \cdots [*]\] の解として定義することもできる. 本問では, この「微分方程式」から指数法則として知られる「関数方程式」$f(x_1+x_2) = f(x_1)f(x_2)$ を導いて, $f(1)$ がネイピア数と一致することを示した. この結果から,「微分方程式」$[*]$ の解が, 高校の教科書で定義される指数関数, つまり $e = \lim\limits_{h \to 0}(1+h)^{\frac{1}{h}}$ を底とする指数関数と一致することがわかる.
- 「微分方程式」$f''(x) = -f(x),$ $f(0) = 1,$ $f'(0) = 0$ の解, $g''(x) = -g(x),$ $g(0) = 0,$ $g'(0) = 1$ の解として, 三角関数 $f(x) = \cos x,$ $g(x) = \sin x$ が定まる.
以下では,「変数分離法」と呼ばれる, 簡単な式変形と積分の計算だけで解ける「微分方程式」の問題を紹介する.
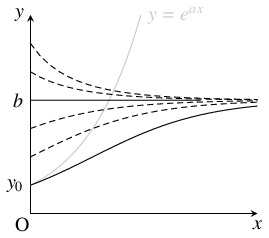
問題《ロジスティック方程式》
$a,$ $b$ を正の数とする.
$x$ の関数 $y$ とその導関数 $y'$ について
\[ y' = ay\left( 1-\frac{y}{b}\right) \quad \cdots [\ast ]\]
が成り立つとする.
また, $x = 0$ のとき $y = y_0 > 0$ であり, すべての $x$ に対して $y \neq 0,$ $b$ であるとする.
- (1)
- $y$ を $x$ の関数として表せ.
- (2)
- $x \to \infty$ のとき $y \to b$ であり, $b > y_0$ であるならば $y$ は単調増加であることを示せ.
解答例
- (1)
- $[*]$ を変形すると \[\begin{aligned} [\ast ] & \iff y' = a\cdot\frac{y(b-y)}{b} \\ &\iff \frac{b}{y(b-y)}\cdot y' = a \\ &\iff \left(\frac{1}{y}+\frac{1}{b-y}\right) y' = a \quad \cdots [1] \end{aligned}\] となるから, 両辺を $x$ で積分すると \[\begin{aligned} [1] &\iff \int\left(\frac{1}{y}+\frac{1}{b-y}\right) y'\,dx = \int a\,dx \\ &\iff \int\left(\frac{1}{y}+\frac{1}{b-y}\right)\,dy = \int a\,dx \\ &\iff \log |y|-\log |b-y| = ax+C \\ &\iff \log\left|\frac{y}{b-y}\right| = ax+C \\ &\iff \left|\frac{y}{b-y}\right| = e^{ax+C} \\ &\iff\frac{y}{b-y} = \pm e^{ax+C} \quad \cdots [2] \end{aligned}\] となる. ここで, $C$ は積分定数である. $c = \pm e^C$ とおくと, \[\begin{aligned} [2] &\iff \frac{y}{b-y} = ce^{ax} \iff y = ce^{ax}(b-y) \\ &\iff (1+ce^{ax})y = bce^{ax} \\ &\iff y = \frac{bce^{ax}}{1+ce^{ax}} \quad \cdots [3] \end{aligned}\] となる. また, $x = 0$ のとき $y = y_0$ であるから, $y_0 = \dfrac{bc}{1+c}$ よって $c = \dfrac{y_0}{b-y_0}$ である. これを $[3]$ に代入して整理すると, \[ y = \frac{by_0e^{ax}}{b-y_0+y_0e^{ax}} \quad \cdots [3]'\] となる.
- (2)
- $[3]'$ から, \[ y = \frac{by_0}{(b-y_0)e^{-ax}+y_0} \quad \cdots [4]\] であるので, \[ y \to \frac{by_0}{y_0} = b \quad (x \to \infty )\] が成り立つ. また, $b > y_0$ であるならば, $y_0 > 0$ と $[4]$ から, $y > 0$ であり, \[\frac{1}{y} = \frac{(b-y_0)e^{-ax}+y_0}{by_0}\] は単調に減少するから, $y$ は単調に増加する.
参考
- 「微分方程式」は, さまざまな現象の解析に応用されている.
例えば, 人口 $y$ の時間変化をモデル化した「微分方程式」の $1$ つに「ロジスティック方程式」(logistic equation) $[*]$ がある.
マルサスが『人口論』で論じた “ 人口は指数関数的に増加する ” という考えのもとでは, 人口 $y$ の時間変化は $y' = ay$ ($a$: 定数) という単純な「微分方程式」で記述できる.
しかし, この人口増加モデルには, 限られた資源環境の中で人口が飽和状態に近づいていくことを説明できないという難点があった.
そこで考案されたのが「ロジスティック方程式」である (フェルフルスト, $1838$ 年).
$[\ast ]$ において, 項 $-\dfrac{ay^2}{b}$ は人口の増加を抑制する役割を果たし, 定数 $b$ は「環境許容量」(carrying capacity of environment) と呼ばれる.
- 「ロジスティック方程式」は,「変数分離法」(variable separation method) という手法で解ける代表的な「微分方程式」である. 例えば,「微分方程式」$y' = -2xy$ $(y \neq 0)$ は, 左辺を $y$ だけの式, 右辺を $x$ だけの式とした \[\frac{y'}{y} = -2x\] の形に変形することで, $\displaystyle\int\frac{y'}{y}\,dx = \int (-2x)\,dx$ から, 置換積分法により $\displaystyle\int\frac{dy}{y} = \int (-2x)\,dx,$ $\log |y| = -x^2+C$ ($C$: 積分定数), $y = ce^{-x^2}$ ($c = \pm e^C$) と解くことができる. このような「微分方程式」の解法を「変数分離法」と呼ぶ.
- 「ロジスティック方程式」の「差分化」により「ロジスティック写像」(こちらを参照) が得られる.
問題《排水時の水位に関する微分方程式》
$a,$ $y_0$ を正の数とする.
$x$ の関数 $y$ について, $x = 0$ のとき $y = y_0$ であり,
\[\frac{dy}{dx} = -a\sqrt y\]
が成り立つ.
- (1)
- $y$ を $x$ の関数として表せ.
- (2)
- $y = 0$ のときの $x$ の値を求めよ.
(参考: $2006$ 京都大)
解答例
- (1)
- \[\frac{1}{\sqrt y}\cdot\frac{dy}{dx} = -a\]
の両辺を $x$ について積分すると,
が得られる. ここで $x = 0$ とすると $2\sqrt{y_0} = C$ となるから,
$2\sqrt y = -ax+C$ ($C$: 定数) である.$2\sqrt y = 2\sqrt{y_0}-ax$ つまり $y = \left(\sqrt{y_0}-\dfrac{a}{2}x\right) ^2$ - (2)
- (1) の結果から, $y = 0$ のとき,
である.
$\left(\sqrt{y_0}-\dfrac{a}{2}x\right) ^2 = 0$ つまり $x = \dfrac{2\sqrt{y_0}}{a}$
参考
鉛直に立てた柱体形のタンクの穴から液体が流出しているとき, 時刻 $t$ における穴からの液面の高さ $h$ について,
\[ S\cdot\frac{dh}{dt} = -s\cdot C_d\sqrt{2gh}\]
($S$: 柱体の底面積, $s$: 穴の面積, $C_d$: 流量計数, $g$: 重力加速度) という「微分方程式」の成り立つことが知られている.
流体力学の「トリチェリの定理」により, $C_d\sqrt{2gh}$ は流出する液体の速さを表す.
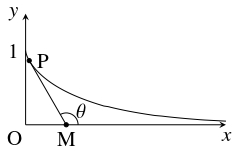
問題《牽引線の媒介変数表示》
-
犬と飼い主が伸び縮みのしない長さ $1$ のリードでつながれている.
飼い主が $xy$ 平面上の原点 $\mathrm O$ から $x$ 軸正方向へ犬を引っ張りながら移動するとき, 点 $(0,1)$ にいた犬が描く軌跡を $C$ とおく.
犬が点 $\mathrm P(x,y)$ にいるとき飼い主が点 $\mathrm M$ にいるとして, $x$ 軸正方向と $\mathrm{MP}$ のなす角を $\theta$ とおく.
- (1)
- $x > 0$ のとき, 点 $\mathrm P$ における $C$ の接線の傾き $\dfrac{dy}{dx}$ は直線 $\mathrm{MP}$ の傾きに等しい. $y$ を用いて $\dfrac{dy}{dx}$ を表せ.
- (2)
- $x$ を $y$ の関数として表せ. ただし, $x$ が $y = 1$ において連続であることは証明なしに用いてよい. (ヒント: 途中で $u = \sqrt{1-y^2}$ と置換するとよい.)
- (3)
- $\theta$ を媒介変数として $C$ を表せ.
解答例
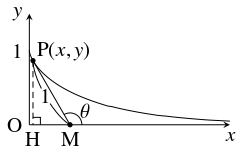
- (1)
- 点 $\mathrm P$ から $x$ 軸に下ろした垂線の足を $\mathrm H$ とおく.
三平方の定理により \[\mathrm{MH} = \sqrt{\mathrm{MP}^2-\mathrm{PH}^2} = \sqrt{1-y^2}\] であるから, \[\frac{dy}{dx} = -\frac{\mathrm{PH}}{\mathrm{MH}} = -\frac{y}{\sqrt{1-y^2}}\] である.
- (2)
- $x > 0$ のとき. (1) から \[ -\frac{\sqrt{1-y^2}}{y}\frac{dy}{dx} = 1\] であるので, \[\begin{aligned} \int dx &= \int\left( -\frac{\sqrt{1-y^2}}{y}\right)\frac{dy}{dx}\,dx \\ x &= -\int\frac{\sqrt{1-y^2}}{y}\,dy \end{aligned}\] が成り立つ. $u = \sqrt{1-y^2}$ とおく. このとき, $u^2 = 1-y^2$ から \[ y = \sqrt{1-u^2}, \quad \frac{dy}{du} = \frac{-u}{\sqrt{1-u^2}}\] であるので, \[\begin{aligned} x &= -\int\frac{\sqrt{1-y^2}}{y}\frac{dy}{du}\,du \\ &= -\int\frac{u}{\sqrt{1-u^2}}\frac{-u}{\sqrt{1-u^2}}\,du \\ &= \int\frac{u^2}{1-u^2}\,du \\ &= -\int du+\int\frac{du}{1-u^2} \quad (\because u^2 = 1-(1-u^2)) \\ &= -\int du+\frac{1}{2}\left(\int\frac{du}{1+u}+\int\frac{du}{1-u}\right) \\ &\qquad \left(\because\frac{1}{1-u^2} = \frac{1}{2}\left(\frac{1}{1+u}+\frac{1}{1-u}\right)\right) \\ &= -u+\frac{1}{2}\{\log (1+u)-\log (1-u)\} +C \\ &= -u+\frac{1}{2}\log\frac{1+u}{1-u}+C \\ &= -\sqrt{1-y^2}+\frac{1}{2}\log\frac{1+\sqrt{1-y^2}}{1-\sqrt{1-y^2}}+C \\ &= -\sqrt{1-y^2}+\frac{1}{2}\log\frac{(1+\sqrt{1-y^2})^2}{y^2}+C \\ &= -\sqrt{1-y^2}+\log\frac{1+\sqrt{1-y^2}}{y}+C \end{aligned}\] が成り立つ ($C$: 積分定数). ここで, $x$ は $y = 1$ において連続であり, $y = 1$ のとき $x = 0$ であるから, \[ 0 = -\sqrt{1-1^2}+\log\frac{1+\sqrt{1-1^2}}{1}+C\] から $C = 0$ が得られる. よって, \[ x = -\sqrt{1-y^2}+\log\frac{1+\sqrt{1-y^2}}{y}\] である.
- (3)
- $x \geqq 0$ のとき, $\dfrac{\pi}{2} \leqq \theta < \pi$ であり, \[\sqrt{1-y^2} = \sqrt{1-\sin ^2\theta} = |\cos\theta | = -\cos\theta\] が成り立つから, \[\begin{aligned} x &= \cos\theta +\log\frac{1-\cos\theta}{\sin\theta} \\ &= \cos\theta +\log\frac{2\sin ^2\dfrac{\theta}{2}}{2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}} \\ &= \cos\theta +\log\tan\frac{\theta}{2} \end{aligned}\] である. ゆえに, $C$ は \[\begin{cases} x = \cos\theta +\log\tan\dfrac{\theta}{2}, & {} \\ y = \sin\theta & {} \end{cases} \quad \left(\frac{\pi}{2} \leqq \theta < \pi\right)\] と表される.
参考
- \[\begin{cases}
x = a\left(\cos\theta +\log\tan\dfrac{\theta}{2}\right), & {} \\
y = a\sin\theta & {}
\end{cases} \quad (0 < \theta < \pi )\]
($a$: 正の数) で定まる曲線を「牽引線」または「トラクトリックス」(tractrix) と呼ぶ.
この曲線は, 媒介変数の取り方を変えれば,
\[\begin{cases}
x = a\left( -\sin t +\log\tan\dfrac{2t+\pi}{4}\right), & {} \\
y = a\cos t & {}
\end{cases} \quad \left( -\frac{\pi}{2} < t < \frac{\pi}{2}\right)\]
で表すこともできる.
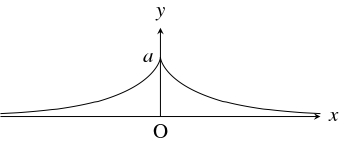
- 伸び縮みのしないひもをある図形にたるみなく巻きつけていくとき, またはそれをたるみなくほどいていくとき, ひもの先端が描く軌跡はその図形の「伸開線」または「インボリュート」(involute) と呼ばれる. 「牽引線」は「懸垂線」$y = a\cdot\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}$ ($a$: 正の数) の「伸開線」であることとが知られている.
