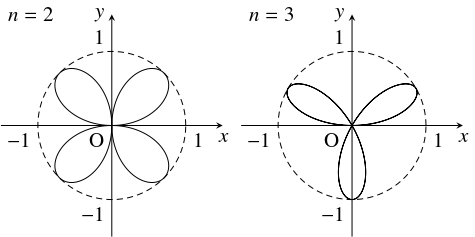面積 (理系)
面積 (陽関数表示)
定理《関数のグラフと直線が囲む図形の面積》
閉区間 $a \leqq x \leqq b$ で定義された連続関数 $f(x),$ $g(x)$ に対して,
曲線 $y = f(x),$ $y = g(x)$ と直線 $x = a,$ $x = b$ で囲まれた図形の面積 $S$ は
\[ S = \int_a^b|f(x)-g(x)|\,dx\]
である.
問題《ベータ関数と面積》
$\alpha,$ $\beta$ を $\alpha < \beta$ なる実数とし, 非負整数 $m,$ $n$ の各組に対して
\[ I(m,n) = \int_\alpha ^\beta (x-\alpha )^m(\beta -x)^n\,dx\]
と定める.
また, $p,$ $q$ を正の整数とする.
- (1)
- $I(m,0)$ を求めよ.
- (2)
- $n \geqq 1$ のとき, $I(m,n) = \dfrac{n}{m+1}I(m+1,n-1)$ が成り立つことを示せ.
- (3)
- $I(m,n)$ を求めよ.
- (4)
- $B(p,q) = \displaystyle\int_0^1t^{p-1}(1-t)^{q-1}\,dt$ を求めよ.
- (5)
- 曲線 $x^{\frac{1}{p}}+y^{\frac{1}{q}} = 1$ $(0 \leqq x \leqq 1,\ 0 \leqq y \leqq 1)$ と座標軸が囲む図形の面積 $S(p,q)$ を求めよ.
(参考: $2018$ お茶の水女子大, $2015$ 横浜市立大, $2007$ 大阪教育大, $1996$ 高知大, $1986$ 東京工業大 )
解答例
- (1)
- \[\begin{aligned} I(m,0) &= \int_\alpha ^\beta (x-\alpha )^m\,dx = \left[\frac{(x-\alpha )^{m+1}}{m+1}\right] _\alpha ^\beta \\ &= \frac{(\beta -\alpha )^{m+1}}{m+1} \quad \cdots [1] \end{aligned}\] である.
- (2)
- $n \geqq 1$ のとき, \[\begin{aligned} I(m,n) &= \int_\alpha ^\beta\left\{\frac{(x-\alpha )^{m+1}}{m+1}\right\} '(\beta -x)^n\,dx \\ &= \left[\frac{(x-\alpha )^{m+1}}{m+1}(\beta -x)^n\right] _\alpha ^\beta \\ &\qquad -\int_\alpha ^\beta\frac{(x-\alpha )^{m+1}}{m+1}\cdot n(\beta -x)^{n-1}(-1)\,dx \\ &= \frac{n}{m+1}\int_\alpha ^\beta (x-\alpha )^{m+1}(\beta -x)^{n-1}\,dx \\ &= \frac{n}{m+1}I(m+1,n-1) \quad \cdots [2] \end{aligned}\] が成り立つ.
- (3)
- $[1],$ $[2]$ から, \[\begin{aligned} I(m,n) &= \frac{n}{m+1}\cdots \frac{1}{m+n}I(m+n,0) \quad (\because [2]) \\ &= \frac{m!n!}{(m+n)!}\cdot\frac{(\beta -\alpha )^{m+n+1}}{m+n+1} \quad (\because [1]) \\ &= \frac{m!n!}{(m+n+1)!}(\beta -\alpha )^{m+n+1} \quad \cdots [3] \end{aligned}\] が成り立つ.
- (4)
- $\alpha = 0,$ $\beta = 1$ の場合を考えると, $[3]$ から \[ B(p,q) = I(p-1,q-1) = \frac{(p-1)!(q-1)!}{(p+q-1)!} \quad \cdots [4]\] が得られる.
- (5)
- $x^{\frac{1}{p}}+y^{\frac{1}{q}} = 1$ のとき, $y = (1-x^{\frac{1}{p}})^q$ から \[ S(p,q) = \int_0^1(1-x^{\frac{1}{p}})^q\,dx\] である. $t = x^{\frac{1}{p}}$ と置換すると, $x = t^p,$ $\dfrac{dx}{dt} = pt^{p-1}$ となるから, \[\begin{aligned} S(p,q) &= \int_0^1(1-t)^q\cdot pt^{p-1}\,dt = p\cdot B(p,q+1) \\ &= p\cdot\frac{(p-1)!q!}{(p+q)!} = \frac{p!q!}{(p+q)!} \quad (\because [4]) \end{aligned}\] が得られる.
参考
- 定積分 $B(x,y) = \displaystyle\int_0^1t^{x-1}(1-t)^{y-1}\,dt$ $(x,\ y > 0)$ で定まる $x,$ $y$ の関数を「ベータ関数」(beta function) と呼ぶ.
その値 $B(x,y)$ は, $0 < x < 1$ または $0 < y < 1$ のとき「広義積分」(improper integral), つまり定積分の極限 $\displaystyle\lim\limits_{a \to +0}\lim\limits_{b \to 1-0}\int_a^bt^{x-1}(1-t)^{y-1}\,dt$ として定義されるが,
$x,$ $y \geqq 1$ のとき単なる定積分である.
本問では, $p,$ $q$ が正の整数の場合に $B(p,q)$ を求めた.
この場合には, $B(p,q)$ は面積の計算でおなじみの定積分
$\displaystyle\int_\alpha ^\beta (x-\alpha )^m(x-\beta )^n\,dx$ ($m,$ $n$: 非負整数)と密接な関係がある.
- 「ベータ関数」は, $t = \sin ^2\theta$ と置換すると, $1-t = \cos ^2\theta$ となるから, \[\begin{aligned} B(p,q) &= \int_0^{\frac{\pi}{2}}\sin ^{2p-2}\theta\cos ^{2q-2}\theta\cdot 2\sin\theta\cos\theta\,d\theta \\ &= 2\int_0^{\frac{\pi}{2}}\sin ^{2p-1}\theta\cos ^{2q-1}\theta\,d\theta \end{aligned}\] と表される (参考: $2020$ 東北大). この表示からも,「ウォリスの公式」と同様に部分積分を $2$ 回繰り返すことにより, 漸化式 \[ B(p,q) = \frac{q-1}{p}B(p+1,q-1)\] が導かれる.
問題《オイラーの定数にまつわる数列の評価》
$y = \dfrac{1}{x}$ のグラフが下に凸であることを用いて,
\[\sum_{k = 1}^n\frac{1}{k}-\log n > \frac{1}{2}+\frac{1}{2n} \quad (n \geqq 2)\]
であることを示せ.
(参考: 東京理科大)
解答例
曲線 $C:y = \dfrac{1}{x}$ は下に凸であるから,
$2$ 点 $\left( k,\dfrac{1}{k}\right),$ $\left( k+1,\dfrac{1}{k+1}\right)$ を結ぶ直線と $x$ 軸, 直線 $x = k,$ $x = k+1$ が囲む台形の面積は
$C$ と $x$ 軸, 直線 $x = k,$ $x = k+1$ が囲む図形の面積より大きいから,
\[\frac{1}{2}\left(\frac{1}{k}+\frac{1}{k+1}\right)\cdot 1 > \int_k^{k+1}\frac{dx}{x}\]
が成り立つ.
$1 \leqq k \leqq n-1$ なる整数 $k$ に対して辺々を加えると,
\[\begin{aligned}
\frac{1}{2}\sum_{k = 1}^{n-1}\left(\frac{1}{k}+\frac{1}{k+1}\right) &> \int_1^n\frac{dx}{x} \\
\frac{1}{2}\left( 2\sum_{k = 1}^n\frac{1}{k}-\frac{1}{n}-1\right) &> \log n \\
\sum_{k = 1}^n\frac{1}{k}-\log n &> \frac{1}{2}+\frac{1}{2n}
\end{aligned}\]
が得られる.
参考
- 数列 $\displaystyle\left\{\sum_{k = 1}^n\frac{1}{k}-\log n\right\}$ は収束することが知られている. その極限値は,「オイラーの定数」(Euler's constant) と呼ばれ, $\gamma$ で表すことが多い. 本問の結果, 挟みうちの原理により $\gamma \geqq 0.5$ であり, 実際の値は \[\gamma = 0.5772156649\cdots\] である.
- $\gamma$ は数学のさまざまな分野で現れる重要な定数であるが, 有理数, 無理数のどちらであるかは未解決である (無理数であると予想されている).
面積 (陰関数表示)
問題《対称軸が直交する放物線が囲む図形の面積》
$p,$ $q$ を正の数とする.
放物線 $y^2 = 4px,$ $x^2 = 4qy$ が囲む図形の面積を求めよ.
解答例
$y^2 = 4px,$ $x^2 = 4qy$ の交点の $x$ 座標は, $y^2 = 4px,$ $x^4 = 16q^2y^2$ から $y$ を消去した方程式
の解であるから, $x = 0,$ $4\sqrt[3]{pq^2}$ である.
また, $y \geqq 0$ において
\[ y^2 = 4px \iff y = 2\sqrt{px}\]
であるから, 求める面積は
\[\begin{aligned}
\int_0^{4\sqrt[3]{pq^2}}\left( 2\sqrt{px}-\frac{x^2}{4q}\right)\,dx &= \left[ 2\sqrt{p}\cdot\frac{2}{3}x^{\frac{3}{2}}-\frac{1}{4q}\cdot\frac{x^3}{3}\right]_0^{4\sqrt[3]{pq^2}} \\
&= \frac{32}{3}pq-\frac{16}{3}pq = \frac{16}{3}pq
\end{aligned}\]
である.
| $x^4 = 64pq^2x$ つまり $x(x^3-64pq^2) = 0$ |
問題《円の面積》
積分法により, 単位円の面積 $S$ は $S = \pi$ であることを導け.
解答例
単位円は, 不等式 $x^2+y^2 \leqq 1$ つまり
\[ -\sqrt{1-x^2} \leqq y \leqq \sqrt{1-x^2}\]
で表される.
この円は $x$ 軸に関して対称であるから, $S$ は曲線 $y = \sqrt{1-x^2}$ と $x$ 軸が囲む図形の面積の $2$ 倍に等しい.
$x = \cos t\ \left( 0 \leqq t \leqq \dfrac{\pi}{2}\right)$ とおくと,
\[\begin{aligned}
S &= 2\int_{-1}^1\sqrt{1-x^2}\,dx = 4\int _0^1\sqrt{1-x^2}\,dx \\
&= 4\int_{\frac{\pi}{2}}^0\sqrt{1-\cos ^2t}(-\sin t)\,dt \\
&= 4\int_0^\frac{\pi}{2}\sin ^2t\,dt = 2\int_0^\frac{\pi}{2}(1-\cos 2t)\,dt \\
&= 2\left[ t-\frac{\sin 2t}{2}\right] _0^\frac{\pi}{2} = \pi
\end{aligned}\]
が得られる.
別解 1: 媒介変数表示を利用
単位円の周は $x = \cos t,$ $y = \sin t$ $(0 \leqq t \leqq 2\pi )$ で表される.
この円は $x$ 軸に関して対称であるから, $S$ は半円の面積の $2$ 倍であり,
\[\begin{aligned}
S &= 2\int_{-1}^1y\,dx \\
&= 2\int_\pi ^0y\frac{dx}{dt}\,dt = 2\int_\pi ^0\sin t(-\sin t)\,dt \\
&= 2\int_0^\pi\sin ^2t\,dt = \int_0^\pi(1-\cos 2t)\,dt \\
&= \left[ t-\frac{\sin 2t}{2}\right] _0^\pi = \pi
\end{aligned}\]
である.
別解 2: 極方程式で定まる図形の面積の公式を利用
単位円の周は極方程式 $r = 1$ で表されるから, その面積は
\[\begin{aligned}
S &= \frac{1}{2}\int_0^{2\pi}r^2\,d\theta = \frac{1}{2}\int_0^{2\pi}\,d\theta \\
&= \frac{1}{2}\left[\theta\right] _0^{2\pi} = \frac{1}{2}\cdot 2\pi = \pi
\end{aligned}\]
である.
問題《楕円の共通部分の面積》
正の数 $a,$ $b$ $(a > b)$ について, $\beta$ を
\[\sin\beta = \frac{b}{\sqrt{a^2+b^2}}, \quad 0 < \beta < \frac{\pi}{2}\]
なる実数とする.
$a,$ $b,$ $\beta$ を用いて楕円
\[\frac{x^2}{a^2}+\frac{y^2}{b^2} \leqq 1, \quad \frac{x^2}{b^2}+\frac{y^2}{a^2} \leqq 1\]
の共通部分の面積 $S$ を表せ.
(参考: $2007$ 広島大)
解答例
楕円
\[\frac{x^2}{a^2}+\frac{y^2}{b^2} \leqq 1, \quad \frac{x^2}{b^2}+\frac{y^2}{a^2} \leqq 1\]
は $x$ 軸, $y$ 軸に関して対称であり, 互いに直線 $y = x$ に関して対称であるから,
その共通部分は $x$ 軸, $y$ 軸, 直線 $y = x$ に関して対称である.
よって, 求める面積 $S$ は, 楕円の周 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ $(y \geqq 0)$ と $y$ 軸, 直線 $y = x$ が囲む図形の面積の $8$ 倍である.
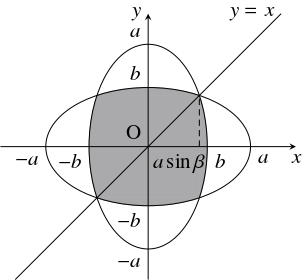 $C$ と直線 $y = x$ の第 $1$ 象限における交点の $x$ 座標は,
$C$ と直線 $y = x$ の第 $1$ 象限における交点の $x$ 座標は,

$\dfrac{x^2}{a^2}+\dfrac{x^2}{b^2} = 1$ つまり $(a^2+b^2)x^2 = a^2b^2$
の解
\[ x = \frac{ab}{\sqrt{a^2+b^2}} = a\sin\beta\]
である.
$y \geqq 0$ において $C$ は $y = \dfrac{b}{a}\sqrt{a^2-x^2}$ と表されるから,
\[\begin{aligned}
\frac{S}{8} &= \int_0^{\frac{ab}{\sqrt{a^2+b^2}}}\frac{b}{a}\sqrt{a^2-x^2}\,dx-\frac{1}{2}\left(\frac{ab}{\sqrt{a^2+b^2}}\right)^2 \\
&= \frac{b}{a}\int_0^{\frac{ab}{\sqrt{a^2+b^2}}}\sqrt{a^2-x^2}\,dx-\frac{a^2b^2}{2(a^2+b^2)}
\end{aligned}\]
である.
$x = a\sin\theta$ とおくと, $\dfrac{dx}{d\theta} = a\cos\theta$ となるから,
\[\begin{aligned}
&\int_0^{\frac{ab}{\sqrt{a^2+b^2}}}\sqrt{a^2-x^2}\,dx = \int_0^\beta\sqrt{a^2(1-\sin ^2\theta )}\cdot a\cos\theta\,d\theta \\
&= a^2\int_0^\beta\cos ^2\theta\,d\theta = \frac{a^2}{2}\int_0^\beta (1+\cos 2\theta )\,d\theta \\
&= \frac{a^2}{2}\left[\theta +\frac{1}{2}\sin 2\theta\right] _0^\beta = \frac{a^2}{2}\beta+\frac{a^2}{4}\sin 2\beta
\end{aligned}\]
が得られる.
ゆえに, 求める面積は,
\[\begin{aligned}
S &= \frac{8b}{a}\left(\frac{a^2}{2}\beta +\frac{a^2}{4}\sin 2\beta\right) -\frac{4a^2b^2}{a^2+b^2} \\
&= 4ab\beta +4ab\sin\beta\cos\beta -\frac{4a^2b^2}{a^2+b^2} \\
&= 4ab\beta +4ab\cdot\frac{b}{\sqrt{a^2+b^2}}\cdot\frac{a}{\sqrt{a^2+b^2}}-\frac{4a^2b^2}{a^2+b^2} \\
&= 4ab\beta
\end{aligned}\]
である.
問題《リサジュー曲線が囲む図形の面積: 陰関数表示》
曲線 $C:y^2 = 4x^2(1-x^2)$ $(x,\ y \geqq 0)$ と $x$ 軸が囲む図形の面積 $S$ を求めよ.
解答例
$0 \leqq x \leqq 1,$ $y \geqq 0$ であることに注意すると, $y = 2x\sqrt{1-x^2}$ である.
よって, 求める面積は,
\[\begin{aligned}
S &= \int_0^12x\sqrt{1-x^2}\,dx \\
&= -\int_0^1(1-x^2)'\sqrt{1-x^2}\,dx \\
&= -\left[\frac{2}{3}(1-x^2)^{\frac{3}{2}}\right] _0^1 \\
&= \frac{2}{3}
\end{aligned}\]
である.
面積 (媒介変数表示)
問題《リサジュー曲線が囲む図形の面積: 媒介関数表示》
曲線 $C:\begin{cases}
x = \sin\theta, \\
y = \sin 2\theta
\end{cases}\ \left(0 \leqq \theta \leqq \dfrac{\pi}{2}\right)$ と $x$ 軸が囲む図形の面積 $S$ を求めよ.
解答例
$0 \leqq \theta \leqq \dfrac{\pi}{2}$ において $x = \sin\theta$ は単調に増加して, その値の範囲は $0 \leqq x \leqq 1$ である.
また, この範囲で $y = \sin 2\theta \geqq 0$ であるから, 求める面積は
\[\begin{aligned}
S &= \int_0^1y\,dx = \int_0^{\frac{\pi}{2}}y\frac{dx}{d\theta}\,d\theta \\
&= \int_0^{\frac{\pi}{2}}\sin 2\theta\cos\theta\,d\theta = \int_0^{\frac{\pi}{2}}2\sin\theta\cos ^2\theta\,d\theta \\
&= -2\int_0^{\frac{\pi}{2}}\cos ^2\theta (-\sin\theta )\,d\theta = -2\int_0^{\frac{\pi}{2}}\cos ^2\theta (\cos\theta )'\,d\theta \\
&= -2\left[\frac{1}{3}\cos ^3\theta\right] _0^{\frac{\pi}{2}} = \frac{2}{3}
\end{aligned}\]
である.

参考
- $x = A\cos a\theta,$ $y = B\sin (b\theta +\delta )$ ($A,$ $B,$ $a,$ $b$: $0$ でない定数, $\delta$: 定数) の形の方程式で表される曲線は, リサジュー曲線(Lissajous curve) と呼ばれる. これをリサージュ曲線と呼ぶこともあるが, 発音上はリサジュー曲線と呼んだ方がよい.
- この曲線は, $x$ 軸方向の「単振動」と $y$ 軸方向の「単振動」の「合成」によって得られる.
- $a$ と $b$ の比が有理数である場合に限り, この曲線は「閉曲線」になる.
問題《サイクロイドと直線が囲む図形の面積》
- (A)
- サイクロイド \[ x = \theta -\sin\theta, \quad y = 1-\cos\theta \quad (0 \leqq \theta \leqq 2\pi )\] と $x$ 軸が囲む図形の面積 $S$ を求めよ.
- (B)
- カージオイド \[ x = (1+\cos\theta )\cos\theta, \quad y = (1+\cos\theta )\sin\theta \quad (-\pi \leqq \theta \leqq \pi )\] が囲む図形の面積 $S$ を求めよ.
- (C)
- アストロイド \[ x = \cos ^3\theta, \quad y = \sin ^3\theta \quad (0 \leqq \theta \leqq 2\pi )\] が囲む図形の面積 $S$ を求めよ.
解答例
- (A)
- $x$ が $0$ から $2\pi$ まで増加するとき, $\theta$ は $0$ から $2\pi$ まで単調に増加する. $\dfrac{dx}{d\theta} = 1-\cos\theta$ であるから, 求める面積は \[\begin{aligned} S &= \int_0^{2\pi}y\,dx \\ &= \int_0^{2\pi}y\frac{dx}{d\theta}\,d\theta \\ &= \int_0^{2\pi}(1-\cos\theta )^2\,d\theta \\ &= \int_0^{2\pi}(1-2\cos\theta +\cos ^2\theta )\,d\theta \\ &= \int_0^{2\pi}\left(\frac{3}{2}-2\cos\theta +\frac{1}{2}\cos 2\theta\right)\,d\theta \\ &= \left[\frac{3}{2}\theta -2\sin\theta +\frac{1}{4}\sin 2\theta\right] _0^{2\pi} \\ &= \frac{3}{2}(2\pi -0) = 3\pi \end{aligned}\] である.
- (B)
- \[\begin{aligned} \{ 1+\cos (-\theta )\}\cos (-\theta ) &= (1+\cos\theta )\cos\theta \\ \{ 1+\cos (-\theta )\}\sin (-\theta ) &= -(1+\cos\theta )\sin\theta \end{aligned}\] であるから, 曲線の $-\pi \leqq \theta \leqq 0$ の部分と $0 \leqq \theta \leqq \pi$ の部分は $x$ 軸に関して対称である. \[\begin{aligned} \frac{dx}{d\theta} &= -\sin\theta\cos\theta +(1+\cos\theta )(-\sin\theta ) \\ &= -\sin\theta (1+2\cos\theta ) \end{aligned}\] であるから, $\theta$ が $0$ から $\dfrac{2}{3}\pi$ まで増加するとき $x$ は $2$ から $-\dfrac{1}{4}$ まで単調に減少し, $\theta$ が $\dfrac{2}{3}\pi$ から $\pi$ まで増加するとき $x$ は $-\dfrac{1}{4}$ から $0$ まで単調に増加する. $0 \leqq \theta \leqq \dfrac{2}{3}\pi$ の部分の $y$ 座標を $y_1,$ $\dfrac{2}{3}\pi \leqq \theta \leqq \pi$ の部分の $y$ 座標を $y_2$ とおくと, 求める面積は, \[\begin{aligned} &S = 2\left(\int_{-\frac{1}{4}}^2y_1\,dx-\int_{-\frac{1}{4}}^0y_2\,dx\right) \\ &= 2\left[\int_{\frac{2}{3}\pi}^0(1+\cos\theta )\sin\theta\{ -\sin\theta (1+2\cos\theta )\}\,d\theta\right. \\ &\qquad \left.\int_{\frac{2}{3}\pi}^\pi (1+\cos\theta )\sin\theta\{ -\sin\theta (1+2\cos\theta )\}\,d\theta\right] \\ &= 2\int_0^\pi\sin ^2\theta (1+\cos\theta )(1+2\cos\theta )\,d\theta \\ &= 2\int_0^\pi (-2\cos ^4\theta -3\cos ^3\theta +\cos ^2\theta +3\cos\theta +1)\,d\theta \\ &= 2\!\int_0^\pi\left(-\frac{\cos 4\theta}{4}-\frac{3\cos 3\theta}{4}-\frac{\cos 2\theta}{2}+\frac{3\cos\theta}{4}+\frac{3}{4}\right)\,d\theta \\ &= 2\left[ -\frac{\sin 4\theta}{16}-\frac{\sin 3\theta}{4}-\frac{\sin 2\theta}{4}+\frac{3\sin\theta}{4}+\frac{3\theta}{4}\right] _0^\pi \\ &= \frac{3}{2}\pi \end{aligned}\] である.
- (C)
- \[\cos ^3(2\pi -\theta ) = \cos ^3\theta, \quad \sin ^3(2\pi -\theta ) = -\sin ^3\theta\] から曲線の $0 \leqq \theta \leqq \pi$ の部分と $\pi \leqq \theta \leqq 2\pi$ の部分は $x$ 軸に関して対称であり, \[\cos ^3(\pi -\theta ) = -\cos ^3\theta, \quad \sin ^3(\pi -\theta ) = \sin ^3\theta\] から曲線の $0 \leqq \theta \leqq \dfrac{\pi}{2},$ $\dfrac{3}{2}\pi \leqq \theta \leqq 2\pi$ の部分と $\dfrac{\pi}{2} \leqq \theta \leqq \dfrac{3}{2}\pi$ の部分は $y$ 軸に関して対称である. $\theta$ が $0$ から $\dfrac{\pi}{2}$ まで増加するとき, $x$ は $1$ から $0$ まで単調に減少する. $\dfrac{dx}{d\theta} = -3\cos ^2\theta\sin\theta$ であるから, \[\begin{aligned} S &= 4\int_0^1y\,dx \\ &= 4\int_{\frac{\pi}{2}}^0y\dfrac{dx}{d\theta}\,d\theta \\ &= 4\int_{\frac{\pi}{2}}^0\sin ^3\theta (-3\cos ^2\theta\sin\theta )\,d\theta \\ &= 12\int_0^{\frac{\pi}{2}}\sin ^4\theta\cos ^2\theta\,d\theta \\ &= 12\int_0^{\frac{\pi}{2}}\sin ^4\theta (1-\sin ^2\theta )\,d\theta \\ &= 12\int_0^{\frac{\pi}{2}}(\sin ^4\theta -\sin ^6\theta )\,d\theta \end{aligned}\] である. ここで, \[\begin{aligned} &\sin ^4\theta -\sin ^6\theta \\ &= (\sin ^2\theta )^2-(\sin ^2\theta )^3 \\ &= \left(\frac{1-\cos 2\theta}{2}\right) ^2-\left(\frac{1-\cos 2\theta}{2}\right) ^3 \\ &= \frac{1}{8}\left( 1-\cos 2\theta -\cos ^22\theta +\cos ^32\theta\right) \\ &= \frac{1}{8}\left( 1-\cos 2\theta -\frac{1+\cos 4\theta}{2}+\frac{\cos 6\theta +3\cos 2\theta}{4}\right) \\ &= \frac{1}{32}\left( 2-\cos 2\theta -2\cos 4\theta +\cos 6\theta\right) \end{aligned}\] であるから, 求める面積は \[\begin{aligned} S &= \frac{3}{8}\int_0^{\frac{\pi}{2}}\left( 2-\cos 2\theta -2\cos 4\theta +\cos 6\theta\right)\,d\theta \\ &= \frac{3}{8}\left[ 2\theta -\frac{\sin 2\theta}{2}-\frac{\sin 4\theta}{2}+\frac{\sin 6\theta}{6}\right] _0^{\frac{\pi}{2}} \\ &= \frac{3}{8}\pi \end{aligned}\] である.
別解 1: 極方程式で定まる図形の面積の公式を利用
- (B)
- 曲線は極方程式 \[ r = 1+\cos\theta \qquad (-\pi \leqq \theta \leqq \pi )\] で表され, \[ 1+\cos(-\theta ) = 1+\cos\theta\] から $-\pi \leqq \theta \leqq 0$ の部分と $0 \leqq \theta \leqq \pi$ の部分は $x$ 軸に関して対称であるので, 求める面積は \[\begin{aligned} S &= 2\cdot\frac{1}{2}\int_0^\pi r^2\,d\theta \\ &= \int_0^\pi (1+\cos\theta )^2\,d\theta \\ &= \int_0^\pi (1+2\cos\theta +\cos ^2\theta )\,d\theta \\ &= \int_0^\pi\left(\frac{3}{2}+2\cos\theta +\frac{\cos 2\theta}{2}\right)\,d\theta \\ &= \left[\frac{3}{2}\theta +2\sin\theta +\frac{\sin 4\theta}{4}\right] _0^\pi \\ &= \frac{3}{2}\pi \end{aligned}\] である.
別解 2: 「ウォリスの公式」を利用
- (C)
- \[\begin{aligned} S &= 4\int_0^1y\,dx \\ &= 4\int_{\frac{\pi}{2}}^0y\dfrac{dx}{d\theta}\,d\theta \\ &= 4\int_{\frac{\pi}{2}}^0\sin ^3\theta (-3\cos ^2\theta\sin\theta )\,d\theta \\ &= 12\int_0^{\frac{\pi}{2}}\sin ^4\theta\cos ^2\theta\,d\theta \\ &= 12\int_0^{\frac{\pi}{2}}\sin ^4\theta (1-\sin ^2\theta )\,d\theta \\ &= 12\int_0^{\frac{\pi}{2}}(\sin ^4\theta -\sin ^6\theta )\,d\theta \\ &= 12\left(\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2}-\frac{5}{6}\cdot\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2}\right) \\ &= \frac{3}{8}\pi \end{aligned}\] である.
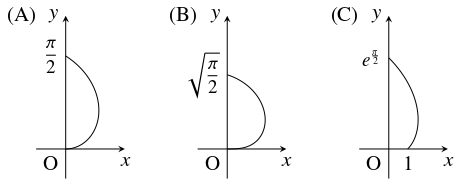
問題《らせんと座標軸が囲む図形の面積》
- (A)
- 曲線 $x = \theta\cos\theta,$ $y = \theta\sin\theta$ $\left( 0 \leqq \theta \leqq \dfrac{\pi}{2}\right)$ と $y$ 軸が囲む図形の面積 $S$ を求めよ.
- (B)
- 曲線 $x = \sqrt\theta\cos\theta,$ $y = \sqrt\theta\sin\theta$ $\left( 0 \leqq \theta \leqq \dfrac{\pi}{2}\right)$ と $y$ 軸が囲む図形の面積 $S$ を求めよ.
- (C)
- 曲線 $x = e^\theta\cos\theta,$ $y = e^\theta\sin\theta$ $\left( 0 \leqq \theta \leqq \dfrac{\pi}{2}\right)$ と $x$ 軸, $y$ 軸が囲む図形の面積 $S$ を求めよ.
解答例
- (A)
- \[\begin{aligned} &S = \int_0^{\frac{\pi}{2}}x\,dy = \int_0^{\frac{\pi}{2}}x\frac{dy}{d\theta}\,d\theta \\ &= \int_0^{\frac{\pi}{2}}\theta\cos\theta\cdot (\sin\theta +\theta\cos\theta )\,d\theta \\ &= \int_0^{\frac{\pi}{2}}\left(\theta\sin\theta\cos\theta +\theta ^2\cos ^2\theta\right)\,d\theta \\ &= \int_0^{\frac{\pi}{2}}\left(\theta\cdot\frac{\sin 2\theta}{2}+\theta ^2\cdot\frac{1+\cos 2\theta}{2}\right)\,d\theta \\ &= \frac{1}{2}\int_0^{\frac{\pi}{2}}\theta ^2\,d\theta +\frac{1}{2}\int_0^{\frac{\pi}{2}}\theta\sin 2\theta\,d\theta +\frac{1}{2}\int_0^{\frac{\pi}{2}}\theta ^2\cos 2\theta\,d\theta \end{aligned}\] であり, \[\begin{aligned} &\int_0^{\frac{\pi}{2}}\theta ^2\cos 2\theta\,d\theta = \int_0^{\frac{\pi}{2}}\theta ^2\left(\frac{\sin 2\theta}{2}\right) '\,d\theta \\ &= \left[\theta ^2\cdot\frac{\sin 2\theta}{2}\right] _0^{\frac{\pi}{2}} -\int_0^{\frac{\pi}{2}}2\theta\cdot\frac{\sin 2\theta}{2}\,d\theta \\ &= -\int_0^{\frac{\pi}{2}}\theta\sin 2\theta\,d\theta \end{aligned}\] であるから, 求める面積は \[ S = \frac{1}{2}\int_0^{\frac{\pi}{2}}\theta ^2\,d\theta = \frac{1}{2}\left[\frac{\theta ^3}{3}\right] _0^{\frac{\pi}{2}} = \frac{\pi ^3}{48}\] である.
- (B)
- \[\begin{aligned} &S = \int_0^{\sqrt{\frac{\pi}{2}}}x\,dy = \int_0^{\frac{\pi}{2}}x\frac{dy}{d\theta}\,d\theta \\ &= \int_0^{\frac{\pi}{2}}\sqrt\theta\cos\theta\cdot\left(\frac{1}{2\sqrt\theta}\cdot\sin\theta +\sqrt\theta\cos\theta\right)\,d\theta \\ &= \int_0^{\frac{\pi}{2}}\left(\frac{\sin\theta\cos\theta}{2}+\theta\cos ^2\theta\right)\,d\theta \\ &= \int_0^{\frac{\pi}{2}}\left(\frac{\sin 2\theta}{4}+\theta\cdot\frac{1+\cos 2\theta}{2}\right)\,d\theta \\ &= \frac{1}{2}\int_0^{\frac{\pi}{2}}\theta\,d\theta +\frac{1}{4}\int_0^{\frac{\pi}{2}}\sin 2\theta\,d\theta +\frac{1}{2}\int_0^{\frac{\pi}{2}}\theta\cos 2\theta\,d\theta \end{aligned}\] であり, \[\begin{aligned} &\int_0^{\frac{\pi}{2}}\theta\cos 2\theta\,d\theta = \int_0^{\frac{\pi}{2}}\theta\left(\frac{\sin 2\theta}{2}\right) '\,d\theta \\ &= \left[\theta\cdot\frac{\sin 2\theta}{2}\right] _0^{\frac{\pi}{2}} -\int_0^{\frac{\pi}{2}}\frac{\sin 2\theta}{2}\,d\theta \\ &= -\frac{1}{2}\int_0^{\frac{\pi}{2}}\sin 2\theta\,d\theta \end{aligned}\] であるから, 求める面積は \[ S = \frac{1}{2}\int_0^{\frac{\pi}{2}}\theta\,d\theta = \frac{1}{2}\left[\frac{\theta ^2}{2}\right] _0^{\frac{\pi}{2}} = \frac{\pi ^2}{16}\] である.
- (C)
- 求める面積は, \[\begin{aligned} S &= \int_0^{e^{\frac{\pi}{2}}}x\,dy = \int_0^{\frac{\pi}{2}}x\frac{dy}{d\theta}\,d\theta \\ &= \int_0^{\frac{\pi}{2}}e^\theta\cos\theta\cdot e^\theta (\sin\theta +\cos\theta )\,d\theta \\ &= \int_0^{\frac{\pi}{2}}e^{2\theta}(\sin\theta\cos\theta +\cos ^2\theta)\,d\theta \\ &= \int_0^{\frac{\pi}{2}}e^{2\theta}\left(\frac{\sin 2\theta}{2}+\frac{1+\cos 2\theta}{2}\right)\,d\theta \\ &= \frac{1}{2}\int_0^{\frac{\pi}{2}}e^{2\theta}\,d\theta +\frac{1}{2}\int_0^{\frac{\pi}{2}}e^{2\theta}(\sin 2\theta +\cos 2\theta )\,d\theta \\ &= \frac{1}{2}\left[\frac{e^{2\theta}}{2}\right] _0^{\frac{\pi}{2}}+\frac{1}{2}\left[\frac{e^{2\theta}\sin 2\theta}{2}\right] _0^{\frac{\pi}{2}} \\ &= \frac{e^\pi -1}{4} \end{aligned}\] である.
別解: 極方程式で定まる図形の面積の公式を利用
- (A)
- \[ x^2+y^2 = \theta ^2(\cos ^2\theta +\sin ^2\theta ) = \theta ^2\] から曲線は極方程式 \[ r = \theta\] で表されるので, 求める面積は \[ S = \frac{1}{2}\int_0^{\frac{\pi}{2}}r^2\,d\theta = \frac{1}{2}\int_0^{\frac{\pi}{2}}\theta ^2\,d\theta = \frac{1}{2}\left[\frac{\theta ^3}{3}\right] _0^{\frac{\pi}{2}} = \frac{\pi ^3}{48}\] である.
- (B)
- \[ x^2+y^2 = \theta (\cos ^2\theta +\sin ^2\theta ) = \theta\] から曲線は極方程式 \[ r = \sqrt\theta\] で表されるので, 求める面積は \[ S = \frac{1}{2}\int_0^{\frac{\pi}{2}}r^2\,d\theta = \frac{1}{2}\int_0^{\frac{\pi}{2}}\theta\,d\theta = \frac{1}{2}\left[\frac{\theta ^2}{2}\right] _0^{\frac{\pi}{2}} = \frac{\pi ^2}{16}\] である.
- (C)
- \[ x^2+y^2 = e^{2\theta}(\cos ^2\theta +\sin ^2\theta ) = e^{2\theta}\] から曲線は極方程式 \[ r = e^\theta\] で表されるので, 求める面積は \[\begin{aligned} S &= \frac{1}{2}\int_0^{\frac{\pi}{2}}r^2\,d\theta = \frac{1}{2}\int_0^{\frac{\pi}{2}}e^{2\theta}\,d\theta \\ &= \frac{1}{2}\left[\frac{e^{2\theta}}{2}\right] _0^{\frac{\pi}{2}} = \frac{e^\pi -1}{4} \end{aligned}\] である.
参考
問題《面積による双曲線関数の特徴付け》
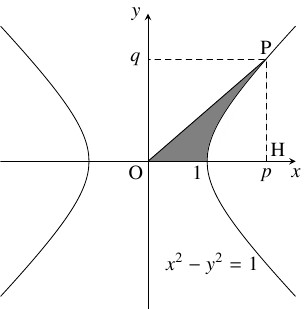
$p = \dfrac{e^\theta +e^{-\theta}}{2},$ $q = \dfrac{e^\theta -e^{-\theta}}{2}$ $(\theta > 0)$ とおき, $xy$ 平面上に点 $\mathrm P(p,q)$ をとる.
- (1)
- 点 $\mathrm P$ は双曲線 $C:x^2-y^2 = 1$ 上にあることを示せ.
- (2)
- $C$ と直線 $\mathrm{OP},$ $x$ 軸が囲む図形の面積 $S$ を, $\theta$ を用いて表せ.
解答例
- (1)
- \[ p^2-q^2 = \frac{e^{2\theta}+2+e^{-2\theta}}{4}-\frac{e^{2\theta}-2+e^{-2\theta}}{4} = 1\] が成り立つから, 点 $\mathrm P$ は双曲線 $C:x^2-y^2 = 1$ 上にある.
- (2)
- $\mathrm H(p,0)$ とおく.
$q > 0$ であり, $y \geqq 0$ のとき
\[ x^2-y^2 = 1 \iff y = \sqrt{x^2-1}\]
であるから,
$S$ は直角三角形 $\mathrm{OHP}$ から曲線 $y = \sqrt{x^2-1}$ と $x$ 軸, 直線 $x = p$ が囲む図形を除いた部分の面積に等しく,
\[ S = \frac{1}{2}pq-\int_1^p\sqrt{x^2-1}\,dx\]
である.
第 $2$ 項で $x = \dfrac{e^t+e^{-t}}{2}$ と置換すると \[\begin{aligned} &\int_1^p\sqrt{x^2-1}\,dx = \int_0^\theta\sqrt{\left(\frac{e^t+e^{-t}}{2}\right) ^2-1}\frac{dx}{dt}\,dt \\ &= \int_0^\theta\sqrt{\left(\frac{e^t-e^{-t}}{2}\right) ^2}\frac{e^t-e^{-t}}{2}\,dt = \int_0^\theta\left(\frac{e^t-e^{-t}}{2}\right) ^2\,dt \\ &= \frac{1}{4}\int_0^\theta (e^{2t}-2+e^{-2t})\,dt = \frac{1}{4}\left[\frac{e^{2t}}{2}-2t-\frac{e^{-2t}}{2}\right] _0^\theta \\ &= \frac{e^{2\theta}-e^{-2\theta}}{8}-\frac{\theta}{2} \end{aligned}\] となるから, $S$ は \[ S = \frac{1}{2}\cdot\frac{e^\theta +e^{-\theta}}{2}\cdot\frac{e^\theta -e^{-\theta}}{2}-\left(\frac{e^{2\theta}-e^{-2\theta}}{8}-\frac{\theta}{2}\right) = \frac{\theta}{2}\] と表される.
参考
$\cosh x = \dfrac{e^x+e^{-x}}{2}\cdots[1],$ $\sinh x = \dfrac{e^x-e^{-x}}{2}\cdots [2]$ はそれぞれ「双曲線余弦関数」, 「双曲線正弦関数」と呼ばれ,
「双曲線正接関数」 $\tanh x = \dfrac{e^x-e^{-x}}{e^x+e^{-x}}$ とあわせて「双曲線関数」(hyperbolic function) と呼ばれる.
$\mathrm E(1,0)$ とおくとき, $\cos\theta,$ $\sin\theta$ は $\angle\mathrm{EOP} = \theta$ なる単位円周 $x^2+y^2 = 1$ 上の点 $\mathrm P$ の $x$ 座標, $y$ 座標として定義されるが, $\theta > 0$ のとき, これは扇形 $\mathrm{OEP}$ の面積が $\dfrac{\theta}{2}$ となる単位円周上の点 $\mathrm P$ の $x$ 座標, $y$ 座標として解釈することもできる.
これと同様に, $0 < \theta < 2\pi$ のとき, $\cosh\theta,$ $\sinh\theta$ は双曲線 $x^2-y^2 = 1$ と直線 $\mathrm{OP},$ $x$ 軸が囲む図形の面積が $\dfrac{\theta}{2}$ であるような双曲線上の点 $\mathrm P$ の $x$ 座標, $y$ 座標として定義できて, $[1],$ $[2]$ が成り立つ.
$\mathrm E(1,0)$ とおくとき, $\cos\theta,$ $\sin\theta$ は $\angle\mathrm{EOP} = \theta$ なる単位円周 $x^2+y^2 = 1$ 上の点 $\mathrm P$ の $x$ 座標, $y$ 座標として定義されるが, $\theta > 0$ のとき, これは扇形 $\mathrm{OEP}$ の面積が $\dfrac{\theta}{2}$ となる単位円周上の点 $\mathrm P$ の $x$ 座標, $y$ 座標として解釈することもできる.
これと同様に, $0 < \theta < 2\pi$ のとき, $\cosh\theta,$ $\sinh\theta$ は双曲線 $x^2-y^2 = 1$ と直線 $\mathrm{OP},$ $x$ 軸が囲む図形の面積が $\dfrac{\theta}{2}$ であるような双曲線上の点 $\mathrm P$ の $x$ 座標, $y$ 座標として定義できて, $[1],$ $[2]$ が成り立つ.
問題《円柱につながれたヤギの問題》
一端が点 $\mathrm A(-1,0)$ に固定された伸び縮みのしない長さ $\pi$ の細いひもが, 円周 $C:x^2+y^2 = 1$ 上に時計回りにたるみなく巻きつけられている.
原点を $\mathrm O,$ 点 $(1,0)$ を $\mathrm E$ とおく.
- (1)
- ひもをたるみなくほどいていくとき, $\mathrm A$ と異なる方のひもの先端を $\mathrm P,$ ひものほどいた部分と $C$ の接点を $\mathrm T$ とおき, $\theta = \angle\mathrm{EOT}$ $(0 \leqq \theta \leqq \pi )$ とおく. このとき, $\theta$ を用いて $\overrightarrow{\mathrm{OP}}$ を表せ.
- (2)
- ひもの先端にヤギをつなぐとき, ヤギが動き回れる範囲の面積を求めよ. ただし, ひものつなぎ目, ヤギの大きさは考えないものとする.
解答例
- (1)
- $\overrightarrow{\mathrm{TP}}$ は $\overrightarrow{\mathrm{OT}} = (\cos\theta,\sin\theta )$ の単位法線ベクトルの $1$ つ $\vec n = (\sin\theta,-\cos\theta )$ を $\stackrel{\frown}{\mathrm{ET}} = \theta$ 倍に伸ばしたベクトルであるから,
$\overrightarrow{\mathrm{OP}}$ は
\[\begin{aligned}
\overrightarrow{\mathrm{OP}} &= \overrightarrow{\mathrm{OT}}+\overrightarrow{\mathrm{TP}} = \overrightarrow{\mathrm{OT}}+\theta\vec n \\
&= (\cos\theta,\sin\theta )+\theta (\sin\theta,-\cos\theta ) \\
&= (\cos\theta +\theta\sin\theta,\sin\theta -\theta\cos\theta )
\end{aligned}\]
と表される.
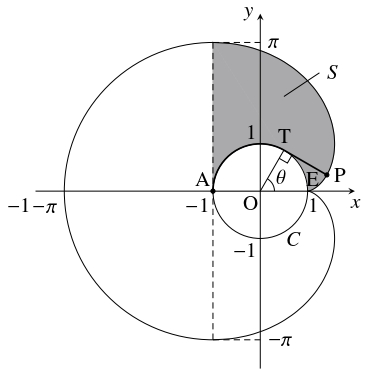
- (2)
- 点 $\mathrm A$ より左側では, ヤギは中心 $\mathrm A,$ 半径 $\pi$ の半円の上を動き回れる. 点 $\mathrm A$ より右側でヤギが動き回れる範囲は $x$ 軸に関して対称であるから, その $x$ 軸より上側の部分の面積を $S$ とおく. それは $0 \leqq \theta \leqq \pi$ におけるひもの先端 $\mathrm P\,(\neq \mathrm A)$ の軌跡と $x$ 軸, 直線 $x = -1$ が囲む図形から円の上半分を除いた部分の面積に等しい. 点 $\mathrm P(x,y)$ について, (1) の結果から \[\begin{aligned} x &= \cos\theta +\theta\sin\theta, \\ y &= \sin\theta -\theta\cos\theta, \\ \frac{dy}{d\theta} &= \cos\theta -\cos\theta +\theta\sin\theta = \theta\sin\theta \end{aligned}\] であるので, \[\begin{aligned} &S+\frac{\pi}{2} = \int_0^\pi\{ x-(-1)\}\,dy \\ &= \int_0^\pi (1+x)\frac{dy}{d\theta}\,d\theta \\ &= \int_0^\pi (1+\cos\theta +\theta\sin\theta )\theta\sin\theta\,d\theta \\ &= \int_0^\pi (\theta\sin\theta +\theta\sin\theta\cos\theta +\theta ^2\sin ^2\theta )\,d\theta \\ &= \int_0^\pi\left(\theta\sin\theta +\theta\cdot\frac{\sin 2\theta}{2}+\theta ^2\cdot\frac{1-\cos 2\theta}{2}\right)\,d\theta \\ &= \int_0^\pi\theta\sin\theta\,d\theta +\frac{1}{2}\int_0^\pi\theta\sin 2\theta\,d\theta \\ &\qquad +\frac{1}{2}\int_0^\pi\theta ^2\,d\theta -\frac{1}{2}\int_0^\pi\theta ^2\cos 2\theta\,d\theta \\ &= [\theta (-\cos\theta )]_0^\pi -\int_0^\pi (-\cos\theta )\,d\theta \\ &\qquad +\frac{1}{2}\left[\theta\cdot\frac{-\cos 2\theta}{2}\right] _0^\pi -\frac{1}{2}\int_0^\pi\frac{-\cos 2\theta}{2}\,d\theta \\ &\qquad +\frac{1}{2}\left[\frac{\theta ^3}{3}\right] _0^\pi -\frac{1}{2}\left[\theta ^2\cdot\frac{\sin 2\theta}{2}\right] _0^\pi +\frac{1}{2}\int_0^\pi 2\theta\cdot\frac{\sin 2\theta}{2}\,d\theta \\ &= \pi +[\sin\theta ]_0^\pi -\frac{\pi}{4}+\frac{1}{4}\left[\frac{\sin 2\theta}{2}\right] _0^\pi \\ &\qquad +\frac{\pi ^3}{6}+\frac{1}{2}\int_0^\pi\theta\sin 2\theta\,d\theta \\ &= \pi-\frac{\pi}{4}+\frac{\pi ^3}{6}-\frac{\pi}{4} \\ &= \frac{\pi ^3}{6}+\frac{\pi}{2} \end{aligned}\] から \[ S = \frac{\pi ^3}{6}\] が得られる. ゆえに, ヤギが動き回れる範囲の面積は, \[\frac{\pi ^3}{2}+2S = \frac{\pi ^3}{2}+2\cdot\frac{\pi ^3}{6} = \frac{5}{6}\pi ^3\] である.
参考
- この種の問題は「ヤギの問題」(goat problem, bull-tethering problem) として知られている. ヤギをつなぐ柱の大きさや形状, ひもの長さなどによって, さまざまな問題が考えられる. 本問では, ヤギが円柱にその周りを $1$ 周できるようにつながれた場合を考えた. ヤギが動き回れる範囲の面積は, 円柱を正多角柱に置き換えた場合 (こちらを参照) の極限値に等しい.
- 伸び縮みのしないひもをある図形にたるみなく巻きつけていくとき, またはそれをたるみなくほどいていくとき, ひもの先端が描く軌跡はその図形の「伸開線」または「インボリュート」(involute) と呼ばれる. 本問で, $0 \leqq \theta \leqq \pi$ のときの点 $\mathrm P$ の軌跡は半円の弧の「伸開線」である.
面積 (極座標表示)
定理《極方程式で表された曲線と直線が囲む図形の面積》
閉区間 $a \leqq \theta \leqq b$ で定義された連続関数 $r(\theta )$ に対して,
極方程式 $r = r(\theta )$ で表された曲線と直線 $\theta = a,$ $\theta = b$ が囲む図形の面積 $S$ は
\[ S = \frac{1}{2}\int_a^br(\theta )^2\,d\theta\]
である.
問題《正葉曲線が囲む図形の面積》
$n$ を $1$ より大きい整数とする.
極方程式 $r = \sin n\theta$ ($n$ が偶数のとき $0 \leqq \theta \leqq 2\pi,$ $n$ が奇数のとき $0 \leqq \theta \leqq \pi$) で表される曲線 $C$ が囲む図形の面積 $S$ を求めよ.
上記の公式は証明なしに使ってよい.
解答例
- (i)
- $n$ が偶数のとき. 求める面積は, \[\begin{aligned} S &= 2n\cdot\frac{1}{2}\int_0^{\frac{\pi}{n}}r^2\,d\theta = n\int_0^{\frac{\pi}{n}}\sin ^2n\theta\,d\theta \\ &= n\int_0^{\frac{\pi}{n}}\frac{1-\cos 2n\theta }{2}\,d\theta = \frac{n}{2}\left[\theta -\frac{\sin 2n\theta}{2n}\right] _0^{\frac{\pi}{n}} \\ &= \frac{n}{2}\cdot\frac{\pi}{n} = \frac{\pi}{2} \end{aligned}\] である.
- (ii)
- $n$ が奇数のとき. 求める面積は, \[\begin{aligned} S &= n\cdot\frac{1}{2}\int_0^{\frac{\pi}{n}}r^2\,d\theta = \frac{n}{2}\int_0^{\frac{\pi}{n}}\sin ^2n\theta\,d\theta \\ &= \frac{n}{2}\int_0^{\frac{\pi}{n}}\frac{1-\cos 2n\theta}{2}\,d\theta = \frac{n}{4}\left[\theta -\frac{\sin 2n\theta}{2n}\right] _0^{\frac{\pi}{n}} \\ &= \frac{n}{4}\cdot\frac{\pi}{n} = \frac{\pi}{4} \end{aligned}\] である.
問題《レムニスケートが囲む図形の面積》
極方程式 $r^2 = 2\cos 2\theta$ $(0 \leqq \theta \leqq \pi )$ で表される曲線 $C$ が囲む図形の面積 $S$ を求めよ.
上記の公式は証明なしに使ってよい.
(参考: $2005$ 鹿児島大)
解答例
$x = r\cos\theta,$ $y = r\sin\theta$ とおくと
\[ x^2+y^2 = r^2, \quad x^2-y^2 = r^2\cos 2\theta\]
となるから, 曲線 $C$ は $xy$ 平面において
\[ (x^2+y^2)^2 = 2(x^2-y^2)\]
で表される.
よって, $C$ は $x$ 軸, $y$ 軸に関して対称であり, $x \geqq 0,$ $y \geqq 0$ の部分は偏角が $0 \leqq \theta \leqq \dfrac{\pi}{4}$ の部分に対応する.
よって, 求める面積は,
\[\begin{aligned}
S &= 4\cdot\frac{1}{2}\int_0^{\frac{\pi}{4}}r^2\,d\theta = 2\int_0^{\frac{\pi}{4}}2\cos 2\theta\,d\theta \\
&= 2[\sin 2\theta ] _0^{\frac{\pi}{4}} = 2
\end{aligned}\]
である.
参考
「レムニスケート」$r^2 = \cos 2\theta$ の長さ $\varpi$ は,「レムニスケート周率」(lemniscate constant) と呼ばれ, 「第 $1$ 種完全楕円積分」(complete elliptic integral of the first kind) と呼ばれる積分
\[ K(k) = \int_0^{\frac{\pi}{2}}\frac{d\theta}{\sqrt{1-k^2\sin ^2\theta}}\]
または「ガンマ関数」${\mathit\Gamma}\,(x)$ を用いて
\[\varpi = 2\int_0^1\frac{dr}{\sqrt{1-r^4}} = \sqrt 2K\left(\frac{1}{\sqrt 2}\right) = \frac{1}{2\sqrt{2\pi}}{\mathit\Gamma}\,\left(\frac{1}{4}\right) ^2\]
と表される.
区分求積法
こちらに移動しました.