(A)

底面積 $S,$ 高さ $h$ の柱体において底面と平行な断面の面積は常に $S$ であるから, 求める体積は \[ V = \int_0^hS\,dx = S\int_0^h\,dx = S[x]_0^h = Sh\] である.

(B)

底面積 $S,$ 高さ $h$ の錐体において底面からの高さが $x$ である断面の面積は $\left(\dfrac{x}{h}\right) ^2S$ であるから, 求める体積は \[ V = \int_0^h\left(\frac{x}{h}\right) ^2S\,dx = \frac{S}{h^2}\int_0^hx^2\,dx = \frac{S}{h^2}\left[\frac{x^3}{3}\right] _0^h = \frac{1}{3}Sh\] である.

(1)

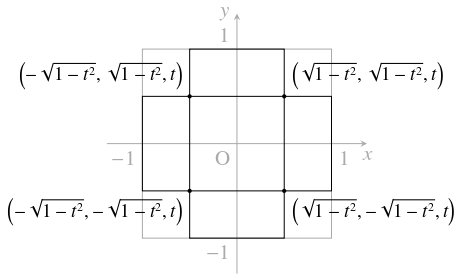
$|x| \leqq 1,$ $|y| \leqq 1$ の範囲で考えれば十分である. $|t| < 1$ のとき, 平面 $z = t$ による各円柱の切り口は, 図のように長方形

$\left\{\begin{array}{l} |x| \leqq 1, \\ |y| \leqq \sqrt{1-t^2} \end{array}\right.$ と $\left\{\begin{array}{l} |y| \leqq 1, \\ |x| \leqq \sqrt{1-t^2} \end{array}\right.$

になるから, 平面 $z = t$ による円柱の共通部分の切り口は正方形 \[\left\{\begin{array}{l} |x| \leqq \sqrt{1-t^2}, \\ |y| \leqq \sqrt{1-t^2} \end{array}\right.\] になる. この面積を $S(t)$ とおくと \[ S(t) = (2\sqrt{1-t^2})^2 = 4(1-t^2) \quad \cdots [1]\] となるから, 求める体積は \[\begin{aligned} V_2 &= \int_{-1}^1S(t)\,dt = 4\int_{-1}^1(1-t^2)\,dt = 8\int_0^1(1-t^2)\,dt \\ &= 8\left[ t-\frac{t^3}{3}\right]_0^1 = 8\left( 1-\frac{1}{3}\right) = \frac{16}{3} \end{aligned}\] である.

(2)

$3$ 本の円柱の共通部分は, 中央の立方体の部分と, その面に接する $6$ つの合同な部分からなる. 立方体の部分について, 面の対角線の長さは円柱の直径 $2$ に等しいから, $1$ 辺の長さは $\sqrt 2$ である. また, $6$ つの合同な部分のうち, $\dfrac{1}{\sqrt 2} \leqq z \leqq 1$ における部分について, 平面 $z = t$ による切り口の面積は $[1]$ の通りである. よって, 求める体積は \[\begin{aligned} V_3 &= (\sqrt 2)^3+6\int_{\frac{1}{\sqrt 2}}^14(1-t^2)\,dt \\ &= 2\sqrt 2+24\int_{\frac{1}{\sqrt 2}}^1(1-t^2)\,dt \\ &= 2\sqrt 2+24\left[ t-\frac{t^3}{3}\right] _{\frac{1}{\sqrt 2}}^1 \\ &= 16-8\sqrt 2 \end{aligned}\] である.

(1)

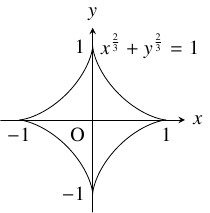
\[\begin{aligned} (\cos ^3\theta )^{\frac{2}{3}}+(\sin ^3\theta )^{\frac{2}{3}} = \cos ^2\theta +\sin ^2\theta = 1 \end{aligned}\] から $C$ は $x,$ $y$ の方程式 \[ x^{\frac{2}{3}}+y^{\frac{2}{3}} = 1\] で表されるので, $C$ は $x$ 軸, $y$ 軸に関して対称であって, $C$ の概形は次の通りである.

よって, $C$ が囲む図形の面積は \[\begin{aligned} S &= 4\int_0^1y\,dx = 4\int_{\frac{\pi}{2}}^0y\frac{dx}{d\theta}\,d\theta \\ &= 4\int_{\frac{\pi}{2}}^0\sin ^3\theta (-3\cos ^2\theta\sin \theta )\,d\theta \\ &= 12\int_0^{\frac{\pi}{2}}\sin ^4\theta\cos ^2\theta\,d\theta \\ &= 12\int_0^{\frac{\pi}{2}}\sin ^4\theta (1-\sin ^2\theta )\,d\theta \\ &= 12\int_0^{\frac{\pi}{2}}(\sin ^4\theta -\sin ^6\theta )\,d\theta \\ &= 12\left(\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2}-\frac{5}{6}\cdot\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2}\right) \\ &= \frac{3}{8}\pi \end{aligned}\] である.

(2)

平面 $z = t$ $(-1 \leqq t \leqq 1)$ による $M$ の断面, つまり曲線 $x^{\frac{2}{3}}+y^{\frac{2}{3}} = 1-t^{\frac{2}{3}},$ $z = t$ が囲む図形の面積を $S(t)$ とおく. このとき, $C$ と曲線 $x^{\frac{2}{3}}+y^{\frac{2}{3}} = a^{\frac{2}{3}}$ の相似比が $1:a$ であることと (1) の結果により \[ S(t) = \frac{3}{8}\pi\left\{ (1-t^{\frac{2}{3}})^{\frac{3}{2}}\right\} ^2 = \frac{3}{8}\pi (1-t^{\frac{2}{3}}) ^3\] となる. $S(t)$ を $t = -1$ から $1$ まで積分すると, $S(t)$ は偶関数であるから, \[\begin{aligned} V &= \int_{-1}^1S(t)\,dt = 2\int_0^1S(t)\,dt \\ &= 2\cdot\frac{3}{8}\pi\int_0^1(1-t^{\frac{2}{3}}) ^3\,dt \\ &= \frac{3}{4}\pi\int_0^1(1-3t^{\frac{2}{3}}+3t^{\frac{4}{3}}-t^2)\,dt \\ &= \frac{3}{4}\pi\left[ t-\frac{9}{5}t^{\frac{5}{3}}+\frac{9}{7}t^{\frac{7}{3}}-\frac{1}{3}t^3\right] _0^1 \\ &= \frac{3}{4}\pi\left( 1-\frac{9}{5}+\frac{9}{7}-\frac{1}{3}\right) \\ &= \frac{4}{35}\pi \end{aligned}\] が得られる.

(A)

半径 $r,$ 高さ $h$ の円柱は直線 $y = r,$ $y = 0,$ $x = 0,$ $x = h$ が囲む図形を $x$ 軸の周りに $1$ 回転させてできるから, 求める体積は \[ V = \pi\int_0^hr^2\,dx = \pi r^2\int_0^h\,dx = \pi r^2[x]_0^h = \pi r^2h\] である.

(B)

半径 $r,$ 高さ $h$ の円錐は直線 $y = \dfrac{r}{h}x,$ $y = 0,$ $x = h$ が囲む図形を $x$ 軸の周りに $1$ 回転させてできるから, 求める体積は \[ V = \pi\!\int_0^h\!\left(\frac{r}{h}x\right) ^2\,dx = \frac{\pi r^2}{h^2}\!\int_0^h\!x^2\,dx = \frac{\pi r^2}{h^2}\left[\frac{x^3}{3}\right] _0^h = \frac{1}{3}\pi r^2h\] である.

　単位球は単位円 $x^2+y^2 \leqq 1$ を $x$ 軸の周りに $1$ 回転させてできる. 対称性により, これは $y = \sqrt{1-x^2}$ と $x$ 軸が囲む図形を $x$ 軸の周りに $1$ 回転させてできるから, 求める体積は \[\begin{aligned} V &= \pi\int_{-1}^1(\sqrt{1-x^2})^2\,dx = \pi\int_{-1}^1(1-x^2)\,dx \\ &= 2\pi\int_0^1(1-x^2)\,dx = 2\pi\left[ x-\frac{x^3}{3}\right] _0^1 \\ &= 2\pi\left( 1-\frac{1}{3}\right) = \frac{4}{3}\pi \end{aligned}\] である.

\[\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 \iff y^2 = \frac{b^2}{a^2}(a^2-x^2)\] であるから, $x$ 軸の周りの回転体の体積は \[\begin{aligned} V_x &= \pi\int_{-a}^ay^2\,dx = \pi\int_{-a}^a\frac{b^2}{a^2}(a^2-x^2)\,dx = \frac{2\pi b^2}{a^2}\int_0^a(a^2-x^2)\,dx \\ &= \frac{2\pi b^2}{a^2}\left[ a^2x-\frac{x^3}{3}\right] _0^a = \frac{4}{3}\pi ab^2 \end{aligned}\] である. 同様に, $y$ 軸の周りの回転体の体積は \[ V_y = \frac{4}{3}\pi a^2b\] である. ゆえに, 求める体積比は \[ V_x:V_y = \frac{4}{3}\pi ab^2:\frac{4}{3}\pi a^2b = b:a\] である.

　$x^2+(y-R)^2 = r^2$ を $y$ について解くと, \[ y = R\pm\sqrt{r^2-x^2}\] となる. 円周の半分 $y = R\pm\sqrt{r^2-x^2}$ と $x$ 軸, 直線 $x = -r,$ $x = r$ で囲まれた図形を $x$ 軸の周りに $1$ 回転させてできる立体の体積を $V_\pm$ (複号同順) とおくと, 求める体積は \[\begin{aligned} V &= V_+-V_- \\ &= \pi\int_{-r}^r(R\!+\!\sqrt{r^2\!-\!x^2})^2\,dx\!-\!\pi\int_{-r}^r(R\!-\!\sqrt{r^2\!-\!x^2})^2\,dx \\ &= 4\pi R\int_{-r}^r\sqrt{r^2-x^2}\,dx = 8\pi R\int_0^r\sqrt{r^2-x^2}\,dx \\ &= 8\pi R\cdot\frac{\pi r^2}{4} = 2\pi ^2r^2R \end{aligned}\] である.

(1)

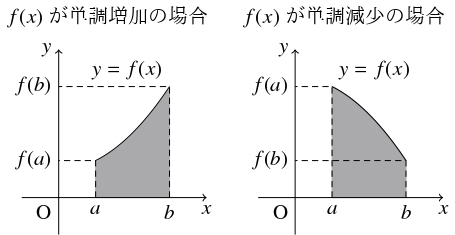
定積分の区間加法性 $\displaystyle\sum_{k = 1}^n\int_{a_{k-1}}^{a_k}\varphi (x)\,dx = \int_{a_0}^{a_n}\varphi (x)\,dx$ により, $f(x)$ が単調増加の場合, 単調減少の場合に示せばよい. $f(x)$ が単調増加または単調減少であるとして, その逆関数を $f^{-1}(x)$ とおく. このとき, 回転体と, 曲線 $x = f^{-1}(y),$ $y$ 軸, 直線 $y = f(a),$ $y = f(b)$ が囲む図形を $y$ 軸のまわりに $1$ 回転させてできる立体の体積の関係から, $f(x)$ が単調増加のとき \[\pi a^2f(a)+V+\pi\int_{f(a)}^{f(b)}f^{-1}(y)^2\,dy = \pi b^2f(b)\] となり, $f(x)$ が単調減少のとき \[\pi a^2f(a)+V = \pi b^2f(b)+\pi\int_{f(b)}^{f(a)}f^{-1}(y)^2\,dy\] となる.

よって, いずれの場合にも \[\begin{aligned} &\pi b^2f(b)-\pi a^2f(a)-V \\ &= \pi\int_{f(a)}^{f(b)}f^{-1}(y)^2\,dy \\ &= \pi\int_a^bx^2f'(x)\,dx \quad (x = f^{-1}(y)) \\ &= \pi\left\{ [x^2f(x)]_a^b-\int_a^b2xf(x)\,dx\right\} \\ &= \pi b^2f(b)-\pi a^2f(a)-2\pi\int_a^bxf(x)\,dx \end{aligned}\] となるから, \[ V = 2\pi\int_a^bxf(x)\,dx\] が得られる.

(2)

円 $(x-R)^2+y^2 \leqq r^2$ は $x$ 軸に関して対称であるから, 求める体積 $V$ は, 半円 $0 \leqq y \leqq \sqrt{r^2-(x-R)^2}$ を $y$ 軸のまわりに $1$ 回転させてできる立体の体積の $2$ 倍である. よって, (1) の結果により, \[\begin{aligned} V &= 2\cdot 2\pi\int_{R-r}^{R+r}x\sqrt{r^2-(x-R)^2}\,dx \\ &= 4\pi\int_{R-r}^{R+r}(x-R)\sqrt{r^2-(x-R)^2}\,dx \\ &\qquad +4\pi R\int_{R-r}^{R+r}\sqrt{r^2-(x-R)^2}\,dx \\ &= 4\pi\int_{-r}^rx\sqrt{r^2-x^2}\,dx+4\pi R\cdot\frac{\pi r^2}{2} \\ &= 2\pi ^2Rr^2 \end{aligned}\] である.