広義積分 (高校発展)
広義積分
問題《ガンマ関数》
$n$ を正の整数とする.
- (1)
- $x > 0$ において $e^x > \dfrac{x^n}{n!}$ が成り立つことを示せ.
- (2)
- $\displaystyle\lim\limits_{x \to \infty}\frac{x^n}{e^x} = 0$ が成り立つことを示せ.
- (3)
- 極限 $\mathit\Gamma\,(n) = \displaystyle\lim\limits_{G \to \infty}\int_0^Gt^{n-1}e^{-t}\,dt$ を求めよ.
(参考: $2018$ 愛知県立大, $2014$ 大分大)
解答例
- (1)
- $f_n(x) = e^x-\dfrac{x^n}{n!}$ $(x \geqq 0)$ とおく.
$f_n(x) > 0$ $(x > 0)$ が成り立つことを数学的帰納法で示す.
- (i)
- $n = 1$ のとき. $f_1(x) = e^x-x$ から, $x > 0$ において, $f_1{}'(x) = e^x-1 > 0$ であるので, $f_1(x)$ の連続性により $f_n(x) = f_1(x) > f_1(0) = 1 > 0$ が成り立つ.
- (ii)
- $n = k$ ($k$: 正の整数) のとき $f_n(x) > 0$ $(x > 0)$ が成り立つとする. このとき, $f_{k+1}(x) = e^x-\dfrac{x^{k+1}}{(k+1)!}$ から, $x > 0$ において, \[ f_{k+1}{}'(x) = e^x-\frac{x^k}{k!} = f_k(x) > 0\] となるので, $f_{k+1}(x)$ の連続性により $f_{k+1}(x) > f_{k+1}(0) = 1 > 0$ となり, $n = k+1$ のとき $f_n(x) > 0$ $(x > 0)$ が成り立つ.
- (2)
- $x > 0$ において, (1) から $e^x > \dfrac{x^{n+1}}{(n+1)!}$ であるので, \[ 0 < \frac{x^n}{e^x} < \frac{(n+1)!}{x}\] が成り立つ. $x \to \infty$ のとき右辺は $0$ に収束するから, 挟みうちの原理により, $\lim\limits_{x \to \infty}\dfrac{x^n}{e^x} = 0$ が成り立つ.
- (3)
- 各正の数 $G$ に対して $\mathit\Gamma _G(n) = \displaystyle\int_0^Gt^{n-1}e^{-t}\,dt$ とおく. $n \geqq 2$ のとき, \[\begin{aligned} \mathit\Gamma _G(n) &= \int_0^Gt^{n-1}(-e^{-t})'\,dt \\ &= \big[ t^{n-1}(-e^{-t})\big] _0^G-\int_0^G(n-1)t^{n-2}(-e^{-t})\,dt \\ &= -G^{n-1}e^{-G}+(n-1)\mathit\Gamma _G(n-1) \end{aligned}\] であるので, $G \to \infty$ のときの極限をとると, (2) の結果から \[\mathit\Gamma\,(n) = (n-1)\mathit\Gamma\,(n-1)\] が得られる. また, \[\begin{aligned} \mathit\Gamma\,(1) &= \lim\limits_{G \to \infty}\int_0^Ge^{-t}\,dt = \lim\limits_{G \to \infty}\big[ -e^{-t}\big] _0^G \\ &= \lim\limits_{G \to \infty}(-e^{-G}+1) = 1 \end{aligned}\] であるから, 正の整数 $n$ に対して \[\mathit\Gamma\,(n) = (n-1)\cdots 1\cdot\mathit\Gamma\,(1) = (n-1)!\] が成り立つ.
参考
- 閉区間 $[a,b]$ における連続関数 $f(x)$ の定積分 $\displaystyle\int_a^bf(x)\,dx$ の $a$ または $b$ に関する極限を「広義積分」(improper integral) と呼ぶ. 例えば, \[\begin{aligned} \int_0^be^{-x}\,dx &= \big[ -e^{-x}\big] _0^b = -e^{-b}+1 \\ &\to 1 \quad (b \to \infty ), \\ \int_a^1\log x\,dx &= \big[ x\log x-x\big] _a^1 = -1-(a\log a-a) \\ &\to -1 \quad (a \to +0) \end{aligned}\] であるから, \[\lim\limits_{b \to \infty}\int_0^be^{-x}\,dx = 1, \quad \lim\limits_{a \to +0}\int_a^1\log x\,dx = -1\] である. ただし, $\lim\limits_{a \to +0}a\log a$ は, $\lim\limits_{t \to \infty}\dfrac{\log t}{t} = 0$ (こちらを参照) から \[\lim\limits_{a \to +0}a\log a = \lim\limits_{a \to +0}\left( -\frac{\log a^{-1}}{a^{-1}}\right) = -\lim\limits_{t \to \infty}\dfrac{\log t}{t} = 0\] と求めた. これらの「広義積分」は, それぞれ \[\int_0^\infty e^{-x}\,dx = 1, \quad \int_0^1\log x\,dx = -1\] と表される.
- 「広義積分」 $\mathit\Gamma\,(x) = \displaystyle\lim\limits_{G \to \infty}\int_0^Gt^{x-1}e^{-t}\,dt$ $(x > 0)$ で定義される関数 $\mathit\Gamma\,(x)$ を「ガンマ関数」(Gamma function) と呼ぶ. 本問で示したように正の整数 $n$ に対して $\mathit\Gamma\,(n) = (n-1)!$ が成り立つから,「ガンマ関数」は階乗の概念を一般化した関数である.
問題《楕円積分の値の評価》
次のことを示せ.
- (1)
- $0 \leqq x < 1$ において \[\frac{1}{\sqrt{1-x^4}} \leqq \dfrac{1}{\sqrt{1-x^2}}\] が成り立つ.
- (2)
- \[\lim_{b \to 1-0}\int_0^b\frac{dx}{\sqrt{1-x^4}} \leqq \frac{\pi}{2}\] である.
解答例
- (1)
- $0 \leqq x < 1$ のとき, $x^4 \leqq x^2 < 1,$ $-1 < -x^4 \leqq -x^2$ すなわち $0 < 1-x^4 \leqq 1-x^2$ から \[ 0 < \sqrt{1-x^4} \leqq \sqrt{1-x^2}\] であるので, \[\frac{1}{\sqrt{1-x^4}} \leqq \frac{1}{\sqrt{1-x^2}} \quad (0 < x < 1) \quad \cdots [1]\] が成り立つ.
- (2)
- $[1]$ により, \[\int_0^b\frac{dx}{\sqrt{1-x^4}} < \int_0^b\frac{dx}{\sqrt{1-x^2}} \quad (0 < b < 1) \quad \cdots [2]\] が成り立つ. $x = \sin\theta$ $(0 \leqq \theta \leqq \beta,$ $b = \sin\beta )$ とおくと, $\dfrac{dx}{d\theta} = \cos\theta$ から, \[\int_0^b\frac{dx}{\sqrt{1-x^2}} = \int_0^\beta\frac{\cos\theta}{\sqrt{1-\sin ^2\theta}}\,d\theta = \int_0^\beta\,d\theta = [\theta ]_0^\beta = \beta\] となる. よって, \[\lim_{b \to 1-0}\int_0^b\frac{dx}{\sqrt{1-x^2}} = \lim_{\beta \to \frac{\pi}{2}-0}\beta = \frac{\pi}{2}\] であるから, $[2]$ により \[\lim_{b \to 1-0}\int_0^b\frac{dx}{\sqrt{1-x^4}} \leqq \frac{\pi}{2}\] である.
参考
- $I = \displaystyle\int_0^1\frac{dx}{\sqrt{1-x^4}}$ は「楕円積分」(elliptic integral) と呼ばれるタイプの「広義積分」で, 値を求めるのが難しい.
- $I$ の値は「レムニスケート」(こちらを参照) $r^2 = \cos 2\theta$ の周の長さ $2\varpi$ の $4$ 分の $1$ つまり $\dfrac{\varpi}{2}$ に等しい. ここで, $\varpi = 2.6220575542\cdots$ は「レムニスケート周率」(lemniscate constant) と呼ばれる定数である.
- 円周率の「レムニスケート周率」に対する比は, $\sqrt 2,$ $1$ の「算術幾何平均」(こちらを参照) に等しいことが知られている.
問題《チェビシェフ多項式の直交性》
すべての正の整数 $n$ に対して
\[ \cos n\theta = T_n(\cos\theta ), \quad \sin (n+1)\theta = \sin\theta\,U_n(\cos\theta )\]
を満たす $n$ 次多項式 $T_n(x),$ $U_n(x)$ が存在する (こちらを参照).
正の整数 $m,$ $n$ に対して,
\[\begin{aligned}
I &= \lim_{a \to -1+0}\lim_{b \to 1-0}\int_a^b\frac{T_m(x)T_n(x)}{\sqrt{1-x^2}}\,dx, \\
J &= \int_{-1}^1U_m(x)U_n(x)\sqrt{1-x^2}\,dx
\end{aligned}\]
の値を求めよ.
ただし, $J$ は
\[ J = \lim_{a \to -1+0}\lim_{b \to 1-0}\int_a^bU_m(x)U_n(x)\sqrt{1-x^2}\,dx\]
と考えるとよい.
解答例
$0 \leqq \theta \leqq \pi$ において, $x = \cos\theta$ $(0 \leqq \theta \leqq \pi )$ とおき, $\cos\theta = a,$ $\cos\theta = b$ の解をそれぞれ $\alpha,$ $\beta$ とおく.
$a \to -1+0$ のとき $\alpha \to \pi -0$ であり, $a \to 1-0$ のとき $\alpha \to +0$ であるから,
\[\begin{aligned}
I &= \lim_{a \to -1+0}\lim_{b \to 1-0}\int_a^b\frac{T_m(x)T_n(x)}{\sqrt{1-x^2}}\,dx \\
&= \lim_{\alpha \to \pi -0}\lim_{\beta \to +0}\int_\alpha ^\beta\frac{T_m(\cos\theta )T_n(\cos\theta )}{\sqrt{1-\cos ^2\theta}}\frac{dx}{d\theta}\,d\theta \\
&= \lim_{\alpha \to \pi -0}\lim_{\beta \to +0}\int_\alpha ^\beta\frac{\cos m\theta\cos n\theta}{\sin\theta}(-\sin\theta )\,d\theta \\
&= -\lim_{\alpha \to \pi -0}\lim_{\beta \to +0}\int_\alpha ^\beta\cos m\theta\cos n\theta\,d\theta \\
&= -\int_\pi ^0\cos m\theta\cos n\theta\,d\theta \\
&= \int_0 ^\pi\cos m\theta\cos n\theta\,d\theta \quad \cdots [1]
\end{aligned}\]
が成り立つ.
- $m \neq n$ のとき. $[1],$ 三角関数の積和の公式により, \[\begin{aligned} I &= \int_0^\pi\frac{\cos (m+n)\theta +\cos (m-n)\theta}{2}\,d\theta \\ &= \frac{1}{2}\left[\frac{\sin (m+n)\theta}{m+n}+\frac{\sin (m-n)\theta}{m-n}\right] _0^\pi \\ &= 0 \end{aligned}\] である.
- $m = n$ のとき. $[1],$ 半角の公式により, \[\begin{aligned} I &= \int_0^\pi\frac{1+\cos 2n\theta}{2}\,d\theta \\ &= \frac{1}{2}\left[ \theta +\frac{\sin 2n\theta}{2n}\right] _0^\pi \\ &= \frac{\pi}{2} \end{aligned}\] である.
- $m \neq n$ のとき. $[2],$ 三角関数の積和の公式により, \[\begin{aligned} J &= \int_0^\pi\frac{\cos (m-n)\theta-\cos (m+n+2)\theta}{2}\,d\theta \\ &= \frac{1}{2}\left[\frac{\sin (m-n)\theta}{m-n}-\frac{\sin (m+n+2)\theta}{m+n+2}\right] _0^\pi \\ &= 0 \end{aligned}\] である.
- $m = n$ のとき. $[2],$ 半角の公式により, \[\begin{aligned} J &= \int_0^\pi\frac{1-\cos 2(n+1)\theta}{2}\,d\theta \\ &= \frac{1}{2}\left[\theta -\frac{\sin 2(n+1)\theta}{2(n+1)}\right] _0^\pi \\ &= \frac{\pi}{2} \end{aligned}\] である.
参考
各正の整数 $n$ に対し,
\[ \cos n\theta = T_n(\cos\theta ), \quad \sin (n+1)\theta = \sin\theta\,U_n(\cos\theta )\]
を満たす $n$ 次多項式 $T_n(x),$ $U_n(x)$ はそれぞれ,「第一種チェビシェフ多項式」,「第二種チェビシェフ多項式」と呼ばれ,
上記の結果により区間 $[-1,1],$ 重み $\dfrac{1}{\sqrt{1-x^2}},$ $\sqrt{1-x^2}$ に関する「直交多項式」であるという.
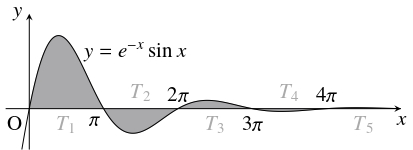
問題《減衰曲線に関する面積の極限》
正の整数 $n$ に対して, 曲線 $y = e^{-x}\sin x$ $(0 \leqq x \leqq n\pi )$ と $x$ 軸が囲む図形の面積の総和を $S_n$ とおく.
極限値 $\lim\limits_{n \to \infty}S_n$ を求めよ.
解答例
\[ T_k = \int_{(k-1)\pi}^{k\pi}e^{-x}|\sin x|\,dx \quad (1 \leqq k \leqq n)\]
とおく.
 このとき,
\[ S_n = \int_0^{n\pi}e^{-x}|\sin x|\,dx = \sum\limits_{k = 1}^nT_k \quad \cdots [1]\]
となる.
$x = t+(k-1)\pi$ とおくと, $0 \leqq t \leqq \pi$ において
\[ |\sin x| = |\sin (t+(k-1)\pi )| = |(-1)^{k-1}\sin t| = \sin t\]
となるから,
\[ T_k = e^{-(k-1)\pi}\int_0^\pi e^{-t}\sin t\,dt\]
となる.
$I = \displaystyle\int e^{-t}\sin t\,dt$ とおくと,
\[\begin{aligned}
I &= \int e^{-t}(-\cos t)'\,dt \\
&= -e^{-t}\cos t-\int e^{-t}\cos t\,dt \\
&= -e^{-t}\cos t-\int e^{-t}(\sin t)'\,dt \\
&= -e^{-t}\cos t-e^{-t}\sin t-I
\end{aligned}\]
から
このとき,
\[ S_n = \int_0^{n\pi}e^{-x}|\sin x|\,dx = \sum\limits_{k = 1}^nT_k \quad \cdots [1]\]
となる.
$x = t+(k-1)\pi$ とおくと, $0 \leqq t \leqq \pi$ において
\[ |\sin x| = |\sin (t+(k-1)\pi )| = |(-1)^{k-1}\sin t| = \sin t\]
となるから,
\[ T_k = e^{-(k-1)\pi}\int_0^\pi e^{-t}\sin t\,dt\]
となる.
$I = \displaystyle\int e^{-t}\sin t\,dt$ とおくと,
\[\begin{aligned}
I &= \int e^{-t}(-\cos t)'\,dt \\
&= -e^{-t}\cos t-\int e^{-t}\cos t\,dt \\
&= -e^{-t}\cos t-\int e^{-t}(\sin t)'\,dt \\
&= -e^{-t}\cos t-e^{-t}\sin t-I
\end{aligned}\]
から
となるので,
\[\begin{aligned}
T_k &= e^{-(k-1)\pi}\left[-\frac{1}{2}e^{-t}(\sin t+\cos t)\right] _0^\pi \\
&= \frac{1+e^{-\pi}}{2}e^{-(k-1)\pi}\quad \cdots [2]
\end{aligned}\]
である.
$[1],$ $[2]$ から, 求める極限値は,
\[\begin{aligned}
\lim\limits_{n \to \infty}S_n &= \lim\limits_{n \to \infty}\sum\limits_{k = 1}^nT_k = \lim\limits_{n \to \infty}\sum\limits_{k = 1}^n\frac{1+e^{-\pi}}{2}e^{-(k-1)\pi} \quad \cdots [3] \\
&= \frac{1+e^{-\pi}}{2}\cdot\frac{1}{1-e^{-\pi}} = \frac{e^{\pi}+1}{2(e^\pi -1)}
\end{aligned}\]
である.
最後から $2$ 番目の等号は, $[3]$ が初項 $\dfrac{1+e^{-\pi}}{2},$ 公比 $e^{-\pi}$ の無限等比級数であることによる.

| $I = -\dfrac{1}{2}e^{-t}(\sin t+\cos t)+C$ ($C$: 定数) |
参考
本問の関数 $y = e^{-x}\sin x$ が表すような, 振幅が指数関数的に小さくなる振動を「減衰振動」という.
問題《アネェージの曲線と漸近線が挟む図形の面積》
$a > 0$ とする.
「アネェージの曲線」$y = \dfrac{a^3}{a^2+x^2}$ (こちらを参照) と $x$ 軸で挟まれた図形の面積 $S$ は,
\[ S = \lim\limits_{A \to \frac{\pi}{2}-0}\int_{-a\tan A}^{a\tan A}\frac{a^3}{a^2+x^2}\,dx\]
と表される.
$S$ の値を求めよ.
解答例
$x = a\tan \theta$ と置換すると, $\dfrac{dx}{d\theta} = \dfrac{a}{\cos ^2\theta}$ から
\[\begin{aligned}
\int_{-a\tan A}^{a\tan A}\frac{a^3}{a^2+x^2}\,dx &= 2a^3\int_0^{a\tan A}\frac{dx}{a^2+x^2} \\
&= 2a^3\int_0^A\frac{1}{a^2(1+\tan ^2\theta )}\cdot\frac{a}{\cos ^2\theta}\,d\theta \\
&= 2a^2\int_0^Ad\theta = 2a^2[\theta ]_0^A = 2a^2A \\
&\to 2a^2\cdot\frac{\pi}{2} = \pi a^2 \quad \left( A \to \frac{\pi}{2}-0\right)
\end{aligned}\]
となるので,
\[ S = \pi a^2\]
である.
問題《牽引線と漸近線が挟む図形の面積》
「牽引線」
\[\begin{cases}
x = \cos\theta +\log\tan\dfrac{\theta}{2}, & {} \\
y = \sin\theta & {}
\end{cases} \quad (0 < \theta < \pi )\]
(こちらを参照) と $x$ 軸で挟まれた図形の面積 $S$ は,
\[ S = \lim_{a \to -\infty}\lim_{b \to \infty}\int_a^by\,dx\]
と表される.
$S$ の値を求めよ.
(参考: $2022$ 東京医科歯科大)
解答例
$0 < \theta < \pi$ において $x = a$ に対応する $\theta$ の値を $\alpha,$ $x = b$ に対応する $\theta$ の値を $\beta$ とおく.
\[\begin{aligned}
\frac{dx}{d\theta} &= -\sin\theta +\frac{1}{\tan\dfrac{\theta}{2}}\cdot\frac{1}{\cos ^2\dfrac{\theta}{2}}\cdot\frac{1}{2} \\
&= -\sin\theta +\frac{1}{2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}} \quad \left(\because\tan\frac{\theta}{2} = \frac{\sin\dfrac{\theta}{2}}{\cos\dfrac{\theta}{2}}\right) \\
&= -\sin\theta +\frac{1}{\sin\theta}
\end{aligned}\]
であり, $a \to -\infty$ のとき $\alpha \to +0,$ $b \to \infty$ のとき $\beta \to \pi -0$ であるから, 求める面積は
\[\begin{aligned}
S &= \lim_{a \to -\infty}\lim_{b \to \infty}\int_a^by\,dx \\
&= \lim_{\alpha \to +0}\lim_{\beta \to \pi -0}\int_\alpha ^\beta y\frac{dx}{d\theta}\,d\theta \\
&= \lim_{\alpha \to +0}\lim_{\beta \to \pi -0}\int_\alpha ^\beta\sin\theta\left( -\sin\theta +\frac{1}{\sin\theta}\right)\,d\theta \\
&= \lim_{\alpha \to +0}\lim_{\beta \to \pi -0}\int_\alpha ^\beta (1-\sin ^2\theta )\,d\theta \\
&= \lim_{\alpha \to +0}\lim_{\beta \to \pi -0}\int_\alpha ^\beta\cos ^2\theta\,d\theta \\
&= \int_0 ^\pi\cos ^2\theta\,d\theta = \int_0 ^\pi\frac{1+\cos 2\theta}{2}\,d\theta \\
&= \frac{1}{2}\left[\theta +\frac{\sin 2\theta}{2}\right] _0^\pi = \frac{\pi}{2}
\end{aligned}\]
である.
参考
- \[\begin{cases}
x = a\left(\cos\theta +\log\tan\dfrac{\theta}{2}\right), & {} \\
y = a\sin\theta & {}
\end{cases} \quad (0 < \theta < \pi )\]
($a$: 正の数) で定まる曲線を「牽引線」または「トラクトリックス」(tractrix) と呼ぶ.
この曲線は, 媒介変数の取り方を変えれば,
\[\begin{cases}
x = a\left( -\sin t +\log\tan\dfrac{2t+\pi}{4}\right), & {} \\
y = a\cos t & {}
\end{cases} \quad \left( -\frac{\pi}{2} < t < \frac{\pi}{2}\right)\]
で表すこともできる.
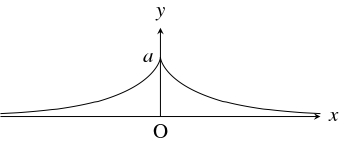
- 犬と飼い主が伸び縮みのしない長さ $a$ のリードでつながれた状態から, 飼い主が犬を引っ張りながら原点から $x$ 軸上を移動するとき, 点 $(0,a)$ にいた犬が描く軌跡は「牽引線」である (こちらを参照).
- 伸び縮みのしないひもをある図形にたるみなく巻きつけていくとき, またはそれをたるみなくほどいていくとき, ひもの先端が描く軌跡はその図形の「伸開線」または「インボリュート」(involute) と呼ばれる. 「牽引線」は「懸垂線」$y = a\cdot\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}$ ($a$: 正の数) の「伸開線」であることとが知られている.
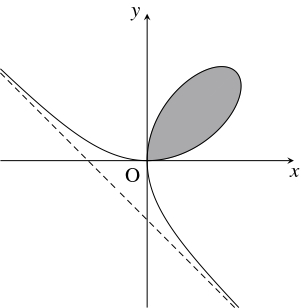
問題《デカルトの葉線で囲まれた図形の面積》
極方程式
\[ r = \frac{3\cos\theta\sin\theta}{\cos ^3\theta+\sin ^3\theta} \quad \left( 0 \leqq \theta \leqq \dfrac{\pi}{2}\right)\]
で表される曲線で囲まれた図形の面積 $S$ を, 次の公式と置き換え $t = \tan\theta$ によって求めよ:
閉区間 $a \leqq \theta \leqq b$ で定義された連続関数 $r(\theta )$ に対して,
極方程式 $r = r(\theta )$ で表される曲線と直線 $\theta = a,$ $\theta = b$ で囲まれた図形の面積 $S$ は
\[ S = \frac{1}{2}\int_a^br(\theta )^2\,d\theta\]
である.
ただし, $\displaystyle\int_0^\infty f(t)\,dt = \lim\limits_{G \to \infty}\int_0^Gf(t)\,dt$ と解釈する.
(参考: $2015$ 横浜市立大)
解答例
\[ r = \frac{3\cdot\dfrac{\sin\theta}{\cos\theta}\cdot\cos ^2\theta}{\left( 1+\dfrac{\sin ^3\theta}{\cos ^3\theta}\right)\cos ^3\theta} = \frac{3\tan\theta}{(1+\tan ^3\theta )\cos\theta}\]
であり, $t = \tan\theta$ とおくと $\dfrac{dt}{d\theta} = \dfrac{1}{\cos ^2\theta}$ となるから,
\[\begin{aligned}
S &= \frac{1}{2}\int_0^{\frac{\pi}{2}}\frac{9\tan ^2\theta}{(1+\tan ^3\theta )^2}\cdot\frac{1}{\cos ^2\theta}\,d\theta \\
&= \frac{1}{2}\int_0^\infty\frac{9t^2}{(1+t^3)^2}\,dt \\
&= \frac{3}{2}\lim\limits_{G \to \infty}\int_0^G\frac{3t^2}{(1+t^3)^2}\,dt \\
&= \frac{3}{2}\lim\limits_{G \to \infty}\int_0^G\frac{(1+t^3)'}{(1+t^3)^2}\,dt \\
&= \frac{3}{2}\lim\limits_{G \to \infty}\left[ -\frac{1}{1+t^3}\right] _0^G \\
&= \frac{3}{2}\lim\limits_{G \to \infty}\left( -\frac{1}{1+G^3}+1\right) = \frac{3}{2}
\end{aligned}\]
が得られる.
参考
- $a > 0$ とする. 直交座標の方程式 $x^3+y^3-3axy = 0,$ または極座標の方程式 $r = \dfrac{3a\cos\theta\sin\theta}{\cos ^3\theta+\sin ^3\theta}$ で定義される曲線 $C$ を「デカルトの葉線」(folium of Descartes) と呼ぶ.
- $C$ で囲まれた図形の面積は $\dfrac{3}{2}a^2$ である.
- 直線 $x+y+a = 0$ は $C$ の漸近線である. 実際, $C$ 上の点 $(x,y)$ について \[\begin{aligned} x^3+y^3+a^3-3axy &= a^3 \\ (x+y+a)(x^2+y^2+a^2-xy-ya-ax) &= a^3 \\ (x+y+a)\{ (x-y)^2+(y-a)^2+(a-x)^2\} &= 2a^3 \end{aligned}\] が成り立つから, \[\begin{aligned} &\lim\limits_{x \to \pm\infty}(x+y+a) \\ &= \lim\limits_{x \to \pm\infty}\frac{2a^3}{(x-y)^2+(y-a)^2+(a-x)^2} = 0 \end{aligned}\] である. これは, 直線 $x+y+a = 0$ が $C$ の漸近線であることを示している.
- $C$ と漸近線 $x+y+a = 0$ で挟まれた部分の面積も $\dfrac{3}{2}a^2$ であることが知られている.
問題《ガブリエルのラッパ》
- (1)
- 双曲線 $y = \dfrac{1}{x}$ と $x$ 軸, 直線 $x = 1,$ $x = G$ $(G > 1)$ で囲まれた図形を $x$ 軸の周りに $1$ 回転させてできる立体 $P_G$ を考える. $G \to \infty$ のとき, $P_G$ の体積 $V_G$ の極限を求めよ.
- (2)
- 区間 $[a,b]$ において連続な関数 $f(x)$ のグラフと $x$ 軸, 直線 $x = a,$ $x = b$ で囲まれた図形を $x$ 軸の周りに $1$ 回転させてできる立体の側面積 $S$ は \[ S = 2\pi\int_a^b|f(x)|\sqrt{1+f'(x)^2}\,dx\] であることが知られている. $G \to \infty$ のとき, (1) の回転体 $P_G$ の側面積 $S_G$ の極限を求めよ.
解答例
- (1)
- \[ V_G = \pi\int_1^G\frac{dx}{x^2} = \pi\left[ -\frac{1}{x}\right] _1^G = \pi\left( -\frac{1}{G}+1\right)\] であるから, 求める極限値 \[\lim\limits_{G \to \infty}V_G = \lim\limits_{G \to \infty}\pi\left( -\frac{1}{G}+1\right) = \pi\] である.
- (2)
- 与えられた公式により \[ S_G = 2\pi\int_1^G\frac{1}{x}\sqrt{1+\left( -\frac{1}{x^2}\right) ^2}\,dx\] であり, $\sqrt{1+\left( -\dfrac{1}{x^2}\right) ^2} \geqq 1$ であるから, \[ S_G \geqq 2\pi\int_1^G\frac{dx}{x} = 2\pi [\log x] _1^G = 2\pi\log G\] が成り立つ. $G \to \infty$ のとき右辺は $\infty$ に発散するから, 追い出しの原理により, 求める極限は \[\lim\limits_{G \to \infty}S_G = \infty\] である.
参考
上記の立体は「ガブリエルのラッパ」(Gabriel's horn) または「トリチェリのトランペット」(Torricelli's trumpet) と呼ばれ, 体積は有限だが, 表面積が無限である立体として有名である.
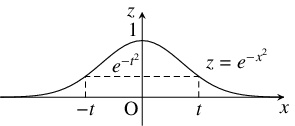
問題《ガウス積分》
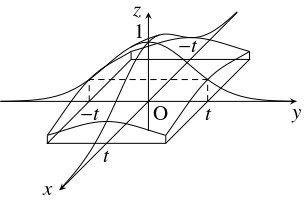
$xyz$ 空間において, 曲線 $z = e^{-x^2},$ $y = 0$ を $z$ 軸の周りに $1$ 回転することで得られる曲面 $z = e^{-x^2-y^2}$ と $xy$ 平面が挟む立体を $M$ とする.
- (1)
- $M$ と円柱 $x^2+y^2 \leqq t^2,$ $0 \leqq z \leqq 1$ の共通部分の体積 $V(t)$ を求めよ.
- (2)
- $M$ と正四角柱 $|x| \leqq t,$ $|y| \leqq t,$ $0 \leqq z \leqq 1$ の共通部分の体積 $W(t)$ を, $\displaystyle\int_{-t}^te^{-x^2}\,dx$ を用いて表せ.
- (3)
- (1), (2) の結果を使って \[\lim\limits_{t \to \infty}\int_{-t}^te^{-x^2}\,dx = \sqrt\pi\] であることを示せ.
(参考: $2015$ 東京工業大, $1989$ 東京大)
解答例
- (1)
- $M$ と円柱 $x^2+y^2 \leqq t^2,$ $0 \leqq z \leqq 1$ の共通部分を平面 $z = e^{-t^2}$ で $2$ つに切り分けて考える.
$z = e^{-x^2}$ のとき, $x^2 = -\log z,$ $z > 0$ であるから,
\[\begin{aligned}
V(t) &= \pi t^2e^{-t^2}+\pi\int _{e^{-t^2}}^1x^2dz \\
&= \pi t^2e^{-t^2}-\pi\int_{e^{-t^2}}^1\log zdz \\
&= \pi t^2e^{-t^2}-\pi\left[ z\log z\right] _{e^{-t^2}}^1+\pi\int _{e^{-t^2}}^1z\cdot\frac{1}{z}dz \\
&= \pi t^2e^{-t^2}+\pi e^{-t^2}\log e^{-t^2}+\pi (1-e^{-t^2}) \\
&= \pi (1-e^{-t^2})
\end{aligned}\]
である.
- (2)
- $M$ と正四角柱 $|x| \leqq t,$ $|y| \leqq t,$ $0 \leqq z \leqq 1$ の共通部分の $x$ 座標が $x$ である断面の面積 $S(x)$ は $S(x) = \displaystyle\int_{-t}^te^{-x^2-y^2}\,dy$ と表されるから,
\[\begin{aligned}
W(t) &= \int_{-t}^tS(x)\,dx \\
&= \int_{-t}^t\left(\int_{-t}^te^{-x^2-y^2}\,dy\right)\,dx \\
&= \int_{-t}^t\left(\int_{-t}^te^{-x^2}e^{-y^2}\,dy\right)\,dx \\
&= \int_{-t}^te^{-x^2}\left(\int_{-t}^te^{-y^2}\,dy\right)\,dx \\
&= \left(\int_{-t}^te^{-y^2}\,dy\right)\left(\int_{-t}^te^{-x^2}\,dx\right) \\
& = \left(\int_{-t}^te^{-x^2}\,dx\right) ^2
\end{aligned}\]
が成り立つ.
- (3)
- $M$ の体積について \[\lim\limits_{t \to \infty}V(t) = \lim\limits_{t \to \infty}W(t)\] が成り立つので, \[\begin{aligned} \left(\lim\limits_{t \to \infty}\int_{-t}^te^{-x^2}\,dx\right) ^2 &= \lim\limits_{t \to \infty}\left(\int_{-t}^te^{-x^2}\,dx\right) ^2 \\ &= \lim\limits_{t \to \infty}\pi (1-e^{-t^2}) \\ &= \pi \end{aligned}\] から, $\displaystyle\lim\limits_{t \to \infty}\int_{-t}^te^{-x^2}\,dx = \sqrt\pi$ である.
参考
- さいころの目のようにとびとびの値をとる変数 (離散的確率変数) に対する確率だけでなく, 長さや時間のように連続した値をとる変数 (連続的確率変数) $X$ に対して確率を考えることもしばしば必要である.
このような確率を考えるには, $X$ に $f(x) \geqq 0$ なる実数値関数 $f(x)$ を対応させて, $a \leqq X \leqq b$ となる確率 $P(a \leqq X \leqq b)$ が定積分 $\displaystyle\int_a^bf(x)\,dx$ の値と一致するようにする.
このとき, $f(x)$ を $X$ の確率密度関数と呼ぶ.
代表的な確率分布の $1$ つである正規分布に従う確率変数の確率密度関数は
であり,「ガウス積分」と呼ばれる「広義積分」$I = \displaystyle\int_{-\infty}^\infty e^{-x^2}\,dx = \lim\limits_{G \to \infty}\int_{-G}^Ge^{-x^2}\,dx$ の値をもとに定まる.
$\dfrac{1}{\sqrt{2\pi\sigma ^2}}e^{-\frac{(x-\mu )^2}{2\sigma ^2}}$ ($\mu$: 期待値, $\sigma ^2$: 分散) - 本問では $e^{-x^2}$ のグラフの回転体の体積を使って $I$ の値を求めたが,「ガウス積分」$I$ は「ガンマ関数」(こちらを参照) を使うと \[\begin{aligned} I &= \lim\limits_{G \to \infty}2\int_0^Ge^{-x^2}\,dx \\ &= \lim\limits_{G \to \infty}2\int_0^Ge^{-u}\cdot\frac{1}{2}u^{-\frac{1}{2}}\,du = \mathit\Gamma\left(\frac{1}{2}\right) \end{aligned}\] と表される. 「ベータ関数」について, 正の整数 $x,$ $y$ に対して \[ B(x,y) = \frac{\mathit\Gamma\,(x)\mathit\Gamma\,(y)}{\mathit\Gamma\,(x+y)}\] が成り立つことは別の問題 (こちらを参照) で示した通りであるが, これは正の数 $x,$ $y$ に対して成り立つことが知られている. $x = y = \dfrac{1}{2}$ にこの公式を適用すると, \[ B\left(\frac{1}{2},\frac{1}{2}\right) = \frac{\mathit\Gamma\left(\dfrac{1}{2}\right)\mathit\Gamma\left(\dfrac{1}{2}\right)}{\mathit\Gamma\,(1)} = I^2\] となる. \[\begin{aligned} B\left(\frac{1}{2},\frac{1}{2}\right) &= \lim\limits_{a \to +0}\lim\limits_{b \to 1-0}\int_a^b\frac{dt}{\sqrt{t(1-t)}} \\ &= \lim\limits_{\alpha \to +0}\lim\limits_{\beta \to \frac{\pi}{2}-0}\int_\alpha ^\beta\frac{2\sin\theta\cos\theta\,d\theta}{\sin\theta\sqrt{1-\sin ^2\theta}} \\ &= \lim\limits_{\alpha \to +0}\lim\limits_{\beta \to \frac{\pi}{2}-0}2\int_\alpha ^\beta d\theta = 2\int_0^{\frac{\pi}{2}}d\theta = \pi \end{aligned}\] であるから, $I = \sqrt\pi$ が成り立つ.
- (2) の解答で現れたような「多変数関数」の積分は「重積分」と呼ばれる.
問題《曲線の等周問題》
- (1)
- 実数値関数 $g(t)$ $(0 \leqq t \leqq \pi )$ は, $g(0) = g(\pi ) = 0$ を満たし, $0 < t < \pi$ において微分可能であり, $g'(t)$ は連続であるとする. $0 \leqq a \leqq \pi$ のとき $g'_\pm (a) = \displaystyle\lim\limits_{h \to \pm 0}\frac{g(a+h)-g(a)}{h}$ (複号同順) と定め, $v(t) = \dfrac{g(t)}{\sin t}$ $(0 < t < \pi )$ とおく. $g'_+(0),$ $g'_-(\pi )$ を用いて $\lim\limits_{\varepsilon \to +0}v(\varepsilon ),$ $\lim\limits_{\varepsilon \to +0}v(\pi -\varepsilon )$ を表せ.
- (2)
- (1) の $g(t)$ に対して, \[\lim\limits_{\varepsilon \to +0}\int_{\varepsilon}^{\pi -\varepsilon}\{ g'(t)^2-g(t)^2\}\,dt \geqq 0\] が成り立つことを示せ. また, 等号が成り立つときの $g(t)$ を求めよ.
- (3)
- $xy$ 平面上の曲線 $C:x = f(t),$ $y = g(t)$ $(0 \leqq t \leqq \pi )$ がある. $0 < t < \pi$ において, $f(t),$ $g(t)$ は微分可能で, $f'(t),$ $g'(t)$ は連続であるとし, $f'(t)^2+g'(t)^2 = 1$ を満たす. さらに, $0 < t < \pi$ において $f'(t) > 0$ であり, $f(0) = g(0) = g(\pi ) = 0$ を満たすとする. $C$ と $x$ 軸が囲む図形の面積を $S$ とおく. このとき, \[ S = \int_0^{f(\pi )}y\,dx = \lim\limits_{\varepsilon \to +0}\int_\varepsilon ^{\pi -\varepsilon}g(t)f'(t)\,dt\] を使って \[ S \leqq \frac{\pi}{2}\] が成り立つことを示せ. また, 等号が成り立つときの $C$ の媒介変数表示を求めよ.
(参考: 山梨大)
解答例
- (1)
- $g(0) = g(\pi ) = 0$ と $g'_+(0),$ $g'_-(\pi )$ の定義から, \[\begin{aligned} \lim\limits_{\varepsilon \to +0}v(\varepsilon ) &= \lim\limits_{\varepsilon \to +0}\frac{g(\varepsilon )-g(0)}{\varepsilon}\cdot\frac{\varepsilon}{\sin\varepsilon} = g'_+(0), \\ \lim\limits_{\varepsilon \to +0}v(\pi -\varepsilon ) &= -\lim\limits_{\varepsilon \to +0}\frac{g(\pi -\varepsilon )-g(\pi )}{-\varepsilon}\cdot\frac{\varepsilon}{\sin\varepsilon} = -g'_-(\pi ) \end{aligned}\] が成り立つ.
- (2)
- $g(t) = v(t)\sin t$ であるから, 積の導関数の公式により
\[\begin{aligned}
&g'(t)^2-g(t)^2 \\
&= \{ v'(t)\sin t+v(t)\cos t\} ^2-v(t)^2\sin ^2t \\
&= v'(t)^2\sin ^2t+2v(t)v'(t)\sin t\cos t+v(t)^2(\cos ^2t -\sin ^2t) \\
&= v'(t)^2\sin ^2t+v(t)v'(t)\sin 2t+v(t)^2\cos 2t \\
&= v'(t)^2\sin ^2t+\frac{1}{2}\{ v(t)^2\sin 2t\} ' \\
&\geqq \frac{1}{2}\{ v(t)^2\sin 2t\} '
\end{aligned}\]
が成り立つ.
よって, $0 < \varepsilon < \pi$ のとき
\[\begin{aligned}
&\int _\varepsilon ^{\pi -\varepsilon}\{ g'(t)^2-g(t)^2\}\,dt \\
&\geqq \frac{1}{2}\int _\varepsilon ^{\pi -\varepsilon}\{ v(t)^2\sin 2t\} '\,dt = \frac{1}{2}[v(t)^2\sin 2t]_\varepsilon ^{\pi -\varepsilon} \\
&= \frac{1}{2}\{ v(\pi -\varepsilon )^2\sin 2(\pi -\varepsilon )-v(\varepsilon )^2\sin 2\varepsilon \}
\end{aligned}\]
であるので, (1) の結果から
\[\begin{aligned}
&\lim\limits_{\varepsilon \to +0}\int _\varepsilon ^{\pi -\varepsilon}\{ g'(t)^2-g(t)^2\}\,dt \\
&\geqq \frac{1}{2}\{ g'_-(\pi )^2\sin 2\pi -g'_+(0) ^2\sin 0\} = 0
\end{aligned}\]
が得られる.
等号成立は, $0 < t < \pi$ において $v'(t)^2\sin ^2t = 0$ つまり $v'(t) = 0$ である場合に限り, このとき, ある実数 $a$ について
となる.
$v(t) = a$ つまり $g(t) = a\sin t$ - (3)
- (2) の結果から,
\[\begin{aligned}
0 &\leqq \lim\limits_{\varepsilon \to +0}\int_{\varepsilon}^{\pi -\varepsilon}\{ g'(t)^2-g(t)^2\}\,dt \\
&= \lim\limits_{\varepsilon \to +0}\int_{\varepsilon}^{\pi -\varepsilon}\{ 1-f'(t)^2-g(t)^2\}\,dt \\
&= \pi -\lim\limits_{\varepsilon \to +0}\int_{\varepsilon}^{\pi -\varepsilon}\{ f'(t)^2+g(t)^2\}\,dt
\end{aligned}\]
が成り立つ.
よって,
\[\begin{aligned}
&\pi -2S \\
&\geqq \lim\limits_{\varepsilon \to +0}\int_{\varepsilon}^{\pi -\varepsilon}\{ f'(t)^2+g(t)^2\}\,dt-2\lim\limits_{\varepsilon \to +0}\int_{\varepsilon}^{\pi -\varepsilon}g(t)f'(t)\,dt \\
&= \lim\limits_{\varepsilon \to +0}\int_{\varepsilon}^{\pi -\varepsilon}\{ f'(t)^2+g(t)^2-2f'(t)g(t)\}\,dt \\
&= \lim\limits_{\varepsilon \to +0}\int_{\varepsilon}^{\pi -\varepsilon}\{ f'(t)-g(t)\} ^2\,dt \geqq 0
\end{aligned}\]
であるから, $2S \leqq \pi$ が成り立つ.
また, 等号成立は,
の場合に限る. このとき, $f(0) = 0$ から, $f(t) = a(1-\cos t)$ である. さらに, $f'(t)^2+g'(t)^2 = 1$ から, $a = 1$ である. ゆえに, 等号が成り立つときの $C$ は \[ x = 1-\cos t, \quad y = \sin t \quad (0 \leqq t \leqq \pi)\] と表される.
$f'(t) = g(t) = a\sin t$ ($a$: 実数) 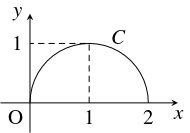
参考
- 周の長さが一定の図形のうち面積が最大の図形を求める問題を「等周問題」と呼ぶ (三角形の場合はこちらとこちらを参照). 本問の結果から, 周の長さ $L$ の曲線と直線が囲む図形の面積 $S$ について, $S \leqq \dfrac{L^2}{\pi ^2}\cdot\dfrac{\pi}{2} = \dfrac{L^2}{2\pi}$ であることがわかる (等号成立は半円の弧の場合). さらに, 周の長さ $L$ の曲線が囲む図形の面積 $S$ について, 周の長さを $2$ 等分する直線によって分けられた部分の面積が $\left(\dfrac{L}{2}\right) ^2\div 2\pi$ 以下であることから, $S \leqq \dfrac{L^2}{4\pi}$ の成り立つことがわかる (等号成立は円周の場合). この不等式は,「等周不等式」と呼ばれる.
- 「等周不等式」の $3$ 次元版として, 凹みのない立体の表面積 $S$ と体積 $V$ について, $36\pi V^2 \leqq S^3$ が成り立ち, 等号は球の場合にのみ成り立つことが知られている.
