不等式の証明
不等式 $A \geqq B$ を示すには, $A-B \geqq 0$ を示すことがしばしば有効である.
平方完成の利用
問題《ヴァイツェンベックの不等式》
- (1)
- 次の各方針に従って, $3$ 辺の長さが $a,$ $b,$ $c$ である三角形の面積 $S$ について
\[ S \leqq \frac{a^2+b^2+c^2}{4\sqrt 3}\]
が成り立つことを示せ.
また, 等号成立条件を求めよ.
- (A)
- 任意の三角形の頂点は, 平行移動, 回転移動, 対称移動により, $\mathrm O(0,0),$ $\mathrm P(h,s),$ $\mathrm Q(h,t)$ ($h,$ $s,$ $t$: 実数, $h > 0,$ $s < t$) に移されることを利用する.
- (B)
- 「ヘロンの公式」(こちらを参照) により, \[\begin{aligned} S &= \frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)} \\ &= \frac{1}{4}\sqrt{2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)} \end{aligned}\] が成り立つことを利用する.
- (2)
- $6$ 辺の長さが $a,$ $b,$ $c,$ $d,$ $e,$ $f$ である四面体の表面積 $T$ について \[ T \leqq \frac{a^2+b^2+c^2+d^2+e^2+f^2}{2\sqrt 3}\] が成り立つことを示せ. また, 等号成立条件を求めよ.
(参考: $2019$ 東京工業大, $1961$ IMO)
実戦定理$2023/06/05$$2023/06/07$
解答例
- (1)
- (A)
- 与えられた三角形の頂点を, 平行移動, 回転移動, 対称移動により, $\mathrm O(0,0),$ $\mathrm P(h,s),$ $\mathrm Q(h,t)$ ($h,$ $s,$ $t$: 実数, $h > 0,$ $s < t$) に移す. このとき, もとの三角形の $3$ 辺の長さ $a,$ $b,$ $c,$ 面積 $S$ は, $\triangle\mathrm{OPQ}$ の $3$ 辺の長さ, 面積に等しい. \[ a = \mathrm{OP}, \quad b = \mathrm{OQ}, \quad c = \mathrm{PQ}\] としても一般性を失わない. \[\begin{aligned} a^2 &= h^2+s^2, \quad b^2 = h^2+t^2, \quad c^2 = (t-s)^2, \\ S &= \frac{(t-s)h}{2} \end{aligned}\] であるから, \[\begin{aligned} &a^2+b^2+c^2-4\sqrt 3S \\ &= (h^2+s^2)+(h^2+t^2)+(t-s)^2-2\sqrt 3(t-s)h \\ &= 2h^2-2\sqrt 3(t-s)h+2(s^2+t^2-st) \\ &= 2\left\{ h-\frac{\sqrt 3}{2}(t-s)\right\} ^2-\frac{3}{2}(t-s)^2+2(s^2+t^2-st) \\ &= 2\left\{ h-\frac{\sqrt 3}{2}(t-s)\right\} ^2+\frac{s^2+t^2+2st}{2} \\ &= 2\left\{ h-\frac{\sqrt 3}{2}(t-s)\right\} ^2+\frac{(s+t)^2}{2} \geqq 0 \end{aligned}\] が成り立つ. ゆえに, \[ S \leqq \frac{a^2+b^2+c^2}{4\sqrt 3}\] が成り立つ. 等号成立は, \[ h-\frac{\sqrt 3}{2}(t-s) = 0, \quad s+t = 0\] つまり \[ s = -\frac{h}{\sqrt 3}, \quad t = \frac{h}{\sqrt 3}\] のとき, すなわち三角形が正三角形であるときに限る.
- (B)
- 「ヘロンの公式」により \[\begin{aligned} &S \leqq \frac{a^2+b^2+c^2}{4\sqrt 3} \quad \cdots [1] \\ &\iff 4\sqrt 3S \leqq a^2+b^2+c^2 \\ &\iff 3(4S)^2 \leqq (a^2+b^2+c^2)^2 \\ &\iff 3\{ 2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)\} \\ &\qquad\quad \leqq (a^4+b^4+c^4)+2(a^2b^2+b^2c^2+c^2a^2) \\ &\iff 4(a^2b^2+b^2c^2+c^2a^2) \leqq 4(a^4+b^4+c^4) \\ &\iff 2(a^4+b^4+c^4)-2(a^2b^2+b^2c^2+c^2a^2) \geqq 0 \\ &\iff (a^2-b^2)^2+(b^2-c^2)^2+(c^2-a^2)^2 \geqq 0 \quad \cdots [2] \end{aligned}\] であり, $[2]$ が成り立つから, $[1]$ が成り立つ. 等号成立は, $a^2 = b^2 = c^2$ つまり $a = b = c$ のとき, すなわち三角形が正三角形であるときに限る.
- (2)
- 四面体 $\mathrm{ABCD}$ において, \[ a = \mathrm{BC},\ b = \mathrm{CA},\ c = \mathrm{AB},\ d = \mathrm{AD},\ e = \mathrm{BD},\ f = \mathrm{CD}\] とおく. (1) の結果により, 各面の面積について, \[\begin{aligned} 4\sqrt 3\triangle\mathrm{ABC} &\leqq a^2+b^2+c^2, \\ 4\sqrt 3\triangle\mathrm{BCD} &\leqq a^2+e^2+f^2, \\ 4\sqrt 3\triangle\mathrm{CAD} &\leqq b^2+f^2+d^2, \\ 4\sqrt 3\triangle\mathrm{ABD} &\leqq c^2+d^2+e^2 \end{aligned}\] が成り立つ. 辺々を加えると \[\begin{aligned} 4\sqrt 3T &\leqq 2(a^2+b^2+c^2+d^2+e^2+f^2) \\ T &\leqq \frac{a^2+b^2+c^2+d^2+e^2+f^2}{2\sqrt 3} \end{aligned}\] が得られる. 等号成立は, 各面が正三角形であるとき, つまり四面体が正四面体であるときに限る.
参考
- (1) の不等式は「ヴァイツェンベックの不等式」(Weitzenböck's inequality) として知られている.
- これは「ハドヴィガー=フィンスラーの不等式」(こちらを参照) から導かれる.
問題《ハドヴィガー=フィンスラーの不等式》
- (1)
- 正の数 $X,$ $Y,$ $Z$ に対して \[\sqrt{3(XY+YZ+ZX)} \leqq X+Y+Z\] が成り立つことを示せ. また, 等号成立条件を求めよ.
- (2)
- $3$ 辺の長さが $a,$ $b,$ $c$ である三角形の面積を $S$ とおく. 「ヘロンの公式」(こちらを参照) により \[ S = \frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}\] が成り立つこと, 変換 $a = y+z,$ $b = z+x,$ $c = x+y,$ (1) の結果を利用して, \[ S \leqq \frac{2ab+2bc+2ca-a^2-b^2-c^2}{4\sqrt 3}\] が成り立つことを示せ. また, 等号成立条件を求めよ.
発展定理$2023/06/07$$2023/10/09$
解答例
- (1)
- \[\begin{aligned} &(X+Y+Z)^2-3(XY+YZ+ZX) \\ &= X^2\!+\!Y^2\!+\!Z^2\!+\!2(XY\!+\!YZ\!+\!ZX)\!-\!3(XY\!+\!YZ\!+\!ZX) \\ &= X^2+Y^2+Z^2-(XY+YZ+ZX) \\ &= \frac{(X-Y)^2+(Y-Z)^2+(Z-X)^2}{2} \geqq 0 \end{aligned}\] であるから, \[ 3(XY+YZ+ZX) \leqq (X+Y+Z)^2\] つまり \[\sqrt{3(XY+YZ+ZX)} \leqq X+Y+Z \quad \cdots [1]\] が成り立つ. 等号成立は, $X = Y = Z$ の場合に限る.
- (2)
- 「ヘロンの公式」により \[ S = \frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}\] であるから, $a = y+z,$ $b = z+x,$ $c = x+y,$ $X = yz,$ $Y = zx,$ $Z = xy$ とすると, $[1]$ により \[\begin{aligned} &2ab+2bc+2ca-a^2-b^2-c^2-4\sqrt 3S \\ &= 2(y+z)(z+x)+2(z+x)(x+y)+2(x+y)(y+z) \\ &\qquad -(y+z)^2-(z+x)^2-(x+y)^2 \\ &\qquad -\sqrt 3\sqrt{2(x+y+z)\cdot 2x\cdot 2y\cdot 2z} \\ &= 2\{ z^2+(x+y)z+xy\} +2\{ x^2+(y+z)x+yz\} \\ &\qquad +2\{ y^2+(z+x)y+zx\} -(y^2+2yz+z^2) \\ &\qquad -(z^2+2zx+x^2)-(x^2+2xy+y^2) \\ &\qquad -4\sqrt{3xyz(x+y+z)} \\ &= 4(xy+yz+zx)-4\sqrt{3xyz(x+y+z)} \\ &= 4\{ (X+Y+Z)-\sqrt{3(XY+YZ+ZX)}\} \geqq 0 \end{aligned}\] が得られるから, \[ S \leqq \frac{2ab+2bc+2ca-a^2-b^2-c^2}{4\sqrt 3}\] が成り立つ. 等号成立は, $X = Y = Z,$ $x = y = z$ つまり $a = b = c$ の場合, すなわち三角形が正三角形である場合に限る.
参考
- (2) の不等式は「ハドヴィガー=フィンスラーの不等式」(Hadwiger–Finsler inequality) として知られている.
- これは \[ S \leqq \frac{a^2+b^2+c^2}{4\sqrt 3}-\frac{(a-b)^2+(b-c)^2+(c-a)^2}{4\sqrt 3}\] と変形できるから,「ヴァイツェンベックの不等式」(こちらを参照) より強い不等式である.
- (2) の不等式は,「ヘロンの公式」を経由せずに, 次のように証明することもできる. 長さが $a,$ $b,$ $c$ である辺の対角の大きさをそれぞれ $A,$ $B,$ $C$ とおく. 余弦定理, 三角形の面積の公式, 半角の公式により \[\begin{aligned} a^2 &= b^2+c^2-2bc\cos A \\ &= (b-c)^2+2bc(1-\cos A) \\ &= (b-c)^2+2\cdot\frac{2S}{\sin A}\cdot 2\sin ^2\frac{A}{2} \\ &= (b-c)^2+8\cdot\frac{S}{2\sin\dfrac{A}{2}\cos\dfrac{A}{2}}\sin ^2\frac{A}{2} \\ &= (b-c)^2+4S\tan\frac{A}{2} \end{aligned}\] が成り立つ. 同様に \[\begin{aligned} b^2 &= (c-a)^2+4S\tan\frac{B}{2}, \\ c^2 &= (a-b)^2+4S\tan\frac{C}{2} \end{aligned}\] も成り立つから, 辺々を加えると \[\begin{aligned} a^2+b^2+c^2 &= (b-c)^2+(c-a)^2+(a-b)^2 \\ &\qquad +4S\left(\tan\frac{A}{2}+\tan\frac{B}{2}+\tan\frac{C}{2}\right) \end{aligned}\] が得られる. $\tan x$ $\left( 0 < x < \dfrac{\pi}{2}\right)$ に関する「イェンセンの不等式」(こちらを参照) により \[\begin{aligned} \tan\frac{A}{2}+\tan\frac{B}{2}+\tan\frac{C}{2} &\geqq 3\tan\frac{A+B+C}{6} \\ &= 3\tan\frac{\pi}{6} = 3\cdot\frac{1}{\sqrt 3} = \sqrt 3 \end{aligned}\] が成り立つから, \[ a^2+b^2+c^2 \geqq (b-c)^2+(c-a)^2+(a-b)^2+4\sqrt 3S\] であり, 展開して整理すると (2) の不等式が得られる.
- $4$ 辺の長さが $a,$ $b,$ $c,$ $d$ である凸四角形の面積 $S$ について \[\begin{aligned} &S \leqq \frac{a^2+b^2+c^2+d^2}{4} \\ &-\!(\sqrt 3\!-\!1)\frac{(a\!-\!b)^2\!\!+\!(a\!-\!c)^2\!\!+\!(a\!-\!d)^2\!\!+\!(b\!-\!c)^2\!\!+\!(b\!-\!d)^2\!\!+\!(c\!-\!d)^2}{4\sqrt 3} \end{aligned}\] が成り立ち, 等号成立は正方形の場合に限ることが知られている (Giugiuc-Oai-Altintas, $2018$).
相加・相乗平均の不等式
定義《相加平均, 相乗平均,調和平均》
正の数 $x_1,$ $\cdots,$ $x_n$ に対して,
\[\frac{x_1+\cdots +x_n}{n}, \quad \sqrt[n]{x_1\cdots x_n}, \quad \frac{n}{x_1{}^{-1}+\cdots +x_n{}^{-1}}\]
をそれぞれ $x_1,$ $\cdots,$ $x_n$ の相加平均 (arithmetic mean), 相乗平均 (geometric mean), 「調和平均」(harmonic mean) と呼ぶ.
参考
上底の長さが $a,$ 下底の長さが $b$ である台形において,
- 相加平均 $\dfrac{a+b}{2}$ つまり $\dfrac{a}{2}+\dfrac{b}{2}$ は, 台形の高さを二等分するような, 斜辺を結び, 底辺と平行な線分の長さを表す.
- 相乗平均 $\sqrt{ab}$ つまり $a:x = x:b$ の解は, 台形を相似な $2$ つの台形に分割するような, 斜辺を結び, 底辺と平行な線分の長さを表す.
- 「調和平均」$\dfrac{2ab}{a+b}$ つまり $\dfrac{a}{a+b}\cdot b+\dfrac{b}{a+b}\cdot a$ は, 台形の対角線の交点を通るような, 斜辺を結び, 底辺と平行な線分の長さを表す.
- 「$2$ 乗平均平方根」$\sqrt{\dfrac{a^2+b^2}{2}}$ つまり $x^2-a^2 = b^2-x^2$ の解は, 台形の面積を二等分するような, 斜辺を結び, 底辺と平行な線分の長さを表す.
定理《相加・相乗平均の不等式》
$2$ 以上の整数 $n,$ 正の数 $x_1,$ $\cdots,$ $x_n$ に対して
\[\frac{x_1+\cdots +x_n}{n} \geqq \sqrt[n]{x_1\cdots x_n} \geqq \frac{n}{x_1{}^{-1}+\cdots +x_n{}^{-1}}\]
が成り立つ.
等号成立は $x_1 = \cdots = x_n$ の場合に限る.
問題《相加・相乗平均の不等式と三角形の等周問題》
- (1)
- $2$ 以上の各整数 $n$ に対して, 次の命題を $p(n)$ とおく: $x_1,$ $\cdots,$ $x_n > 0$ のとき $\dfrac{x_1+\cdots +x_n}{n} \geqq \sqrt[n]{x_1\cdots x_n}$ が成り立ち, 等号成立は $x_1 = \cdots = x_n$ の場合に限る.
- ①
- $p(2)$ と $p(2^i) \Longrightarrow p(2^{i+1})$ ($i$: 正の整数) を示すことにより, すべての正の整数 $m$ に対して $p(2^m)$ が成り立つことを示せ.
- ②
- $2$ 以上の与えられた整数 $n$ に対して, $n \leqq 2^m$ を満たす正の整数 $m$ をとって $p(2^m)$ を使うことにより, $p(n)$ が成り立つことを示せ.
- (2)
- $\triangle\mathrm{ABC}$ において $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $s = \dfrac{a+b+c}{2}$ とおくとき「ヘロンの公式」$\triangle\mathrm{ABC} = \sqrt{s(s-a)(s-b)(s-c)}$ (こちらを参照) が成り立つことを使って, 周の長さが一定の三角形のうち面積が最大のものは正三角形であることを示せ.
(参考: $1987$ 横浜国立大, $1900$'s 大阪市立大)
解答例
- (1)
- ①
- (i)
- $p(2)$ を示す. \[\begin{aligned} \frac{x_1+x_2}{2}-\sqrt{x_1x_2} &= \dfrac{x_1+x_2-2\,\sqrt{x_1x_2}}{2} \\ &= \dfrac{(\,\sqrt{x_1}-\sqrt{x_2})^2}{2} \geqq 0 \end{aligned}\] から, $\dfrac{x_1+x_2}{2} \geqq \sqrt{x_1x_2}$ が成り立つ. 等号成立は, $\sqrt{x_1} = \sqrt{x_2}$ つまり $x_1 = x_2$ の場合に限る. よって, $p(2)$ が成り立つ.
- (ii)
- 与えられた正の整数 $i$ に対して $p(2^i) \Longrightarrow p(2^{i+1})$ が成り立つことを示す. $k = 2^i$ とおき, $p(k)$ が成り立つとする. このとき, \[\begin{aligned} &\frac{x_1+\cdots +x_k+x_{k+1}+\cdots +x_{2k}}{2k} \\ &= \frac{\dfrac{x_1+\cdots +x_k}{k}+\dfrac{x_{k+1}+\cdots +x_{2k}}{k}}{2} \\ &\geqq \frac{\sqrt[k]{x_1\cdots x_k}+\sqrt[k]{x_{k+1}\cdots x_{2k}}}{2} \\ &\geqq \sqrt{\sqrt[k]{x_1\cdots x_k}\,\sqrt[k]{x_{k+1}\cdots x_{2k}}} \\ &= \sqrt[2k]{x_1\cdots x_kx_{k+1}\cdots x_{2k}} \end{aligned}\] が成り立つ. 等号成立は, `` $x_1 = \cdots = x_k,$ $x_{k+1} = \cdots = x_{2k},$ $\sqrt[k]{x_1\cdots x_k} = \sqrt[k]{x_{k+1}\cdots x_{2k}}$ '' つまり $x_1 = \cdots = x_k = x_{k+1} = \cdots = x_{2k}$ の場合に限る. よって, $p(2k)$ が成り立つ. つまり, $p(2^i) \Longrightarrow p(2^{i+1})$ が成り立つ.
- ②
- 与えられた $2$ 以上の整数 $n$ に対して, $n \leqq 2^m$ なる正の整数 $m$ が存在する. $a = \dfrac{x_1+\cdots +x_n}{n}$ とおくと, $p(2^m)$ により \[\begin{aligned} a &= \frac{na+(2^m-n)a}{2^m} = \frac{x_1+\cdots +x_n+(2^m-n)a}{2^m} \\ &\geqq \sqrt[2^m]{x_1\cdots x_na^{2^m-n}} \end{aligned}\] から \[ a^{2^m} \geqq x_1\cdots x_na^{2^m-n}, \quad a^n \geqq x_1\cdots x_n,\] つまり \[ a \geqq \sqrt[n]{x_1\cdots x_n}\] となり, 等号成立は $x_1 = \cdots = x_n = a$ つまり $x_1 = \cdots = x_n$ の場合に限る. ゆえに, $p(n)$ が成り立つ.
- (2)
- 周の長さが $1$ の三角形について考えれば十分である.
この三角形において, $3$ 辺の長さを $a,$ $b,$ $c,$ 面積を $S$ とおく.
「ヘロンの公式」により,
\[ S = \sqrt{\frac{1}{2}\left(\frac{1}{2}-a\right)\left(\frac{1}{2}-b\right)\left(\frac{1}{2}-c\right)}\]
が成り立つ.
よって, (1) における命題 $p(3)$ により,
\[\begin{aligned}
16S^2 &= (1-2a)(1-2b)(1-2c) \\
&\leqq \left\{\frac{(1-2a)+(1-2b)+(1-2c)}{3}\right\} ^3 \\
&= \left\{\frac{3-2(a+b+c)}{3}\right\} ^3 = \left(\frac{3-2\cdot 1}{3}\right) ^3 = \frac{1}{27}
\end{aligned}\]
であり, 等号成立は $1-2a = 1-2b = 1-2c$ つまり $a = b = c$ の場合に限る.}
ゆえに, $S$ は $a = b = c$ の場合に限り最大になるから, 周の長さが一定の三角形のうち面積が最大のものは正三角形である.
参考
- $2$ 以上の整数 $n$ に対して, $x_1,$ $\cdots,$ $x_n > 0$ のとき, \[\frac{x_1+\cdots +x_n}{n} \geqq \sqrt[n]{x_1\cdots x_n} \geqq \frac{n}{x_1{}^{-1}+\cdots +x_n{}^{-1}}\] が成り立ち, 等号成立は $x_1 = \cdots = x_n$ の場合に限る. 左辺を相加平均 (arithmetic mean), 中辺を相乗平均 (geometric mean), 右辺を「調和平均」(harmonic mean) と呼ぶ. (中辺) $\geqq$ (右辺) は, (左辺) $\geqq$ (中辺) において $x_1,$ $\cdots,$ $x_n$ をそれぞれの逆数に置き換えた不等式に同値であるから, (左辺) $\geqq$ (中辺) から従う. 相加・相乗平均の不等式の別証明については, こちらを参照されたい.
- 周の長さが一定の図形のうち面積が最大の図形を求める問題を「等周問題」(isoperimetric problem) と呼ぶ. 本問は三角形の場合であり, 一般に次の定理が成り立つ: 周の長さが $L$ の $n$ 角形の面積 $S$ について, \[ S \leqq \dfrac{L^2}{4n\tan\dfrac{\pi}{n}}\] が成り立ち, 等号成立は正 $n$ 角形の場合に限る. また, 周の長さが一定の「閉曲線」(両端のつながった切れ目のない曲線) が囲む図形のうち面積が最大の図形は円である.
問題《四隅までの距離の和の最小値》
座標平面において, $4$ 点 $\mathrm A(1,1),$ $\mathrm B(-1,1),$ $\mathrm C(-1,-1),$ $\mathrm D(1,-1)$ までの距離の和が最小になるような点の座標を求めよ.
解答例
$\mathrm P(x,y)$ を平面上の任意の点とする.
相加・相乗平均の不等式により,
\[\begin{aligned}
&\mathrm{PA}+\mathrm{PB}+\mathrm{PC}+\mathrm{PD} \\
&\geqq 2\sqrt{\mathrm{PA}\cdot\mathrm{PB}}+2\sqrt{\mathrm{PC}\cdot\mathrm{PD}} = 2(\sqrt{\mathrm{PA}\cdot\mathrm{PB}}+\sqrt{\mathrm{PC}\cdot\mathrm{PD}}) \\
&\geqq 2\cdot 2\sqrt{\sqrt{\mathrm{PA}\cdot\mathrm{PB}}\sqrt{\mathrm{PC}\cdot\mathrm{PD}}} = 4\sqrt[4]{\mathrm{PA}\cdot\mathrm{PB}\cdot\mathrm{PC}\cdot\mathrm{PD}}
\end{aligned}\]
が成り立つ.
等号成立は, $\mathrm{PA} = \mathrm{PB},$ $\mathrm{PC} = \mathrm{PD},$ $\sqrt{\mathrm{PA}\cdot\mathrm{PB}} = \sqrt{\mathrm{PC}\cdot\mathrm{PD}}$ つまり
\[\mathrm{PA} = \mathrm{PB} = \mathrm{PC} = \mathrm{PD}\]
の場合に限る.
この場合, $\mathrm{PA}^2 = \mathrm{PB}^2,$ $\mathrm{PA}^2 = \mathrm{PD}^2$ から
\[\begin{aligned}
(1-x)^2+(1-y)^2 &= (-1-x)^2+(1-y)^2, \\
(1-x)^2+(1-y)^2 &= (1-x)^2+(-1-y)^2
\end{aligned}\]
となり,
\[\begin{aligned}
1-2x+x^2 &= 1+2x+x^2, \\
1-2y+y^2 &= 1+2y+y^2
\end{aligned}\]
となって, $-4x = 0,$ $-4y = 0$ から
\[ x = y = 0\]
となる.
よって, $4$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ までの距離の和が最小値になる点の座標は $(0,0)$ である.
参考
実は, $5$ 本の線分を使うと, 正方形 $\mathrm{ABCD}$ の四隅をもっと短くつなぐことができる (こちらを参照).
この種の問題は「最小シュタイナー木問題」と呼ばれ, 一般に解を求めるのが困難な問題として有名である.
問題《因数分解と $3$ 変数相加・相乗平均の不等式》
- (1)
- \[\begin{aligned} &X^3+Y^3+Z^3-3XYZ \\ &= (X+Y+Z)(X^2+Y^2+Z^2-XY-YZ-ZX) \end{aligned}\] が成り立つことを示せ.
- (2)
- \[\begin{aligned} &2(X^2+Y^2+Z^2-XY-YZ-ZX) \\ &= (X-Y)^2+(Y-Z)^2+(Z-X)^2 \end{aligned}\] が成り立つことを示せ.
- (3)
- $x,$ $y,$ $z \geqq 0$ のとき, $x+y+z \geqq 3\sqrt[3]{xyz}$ が成り立つことを示せ.
解答例
- (1)
- こちらを参照.
- (2)
- $a^2-2ab+b^2 = (a-b)^2$ により \[\begin{aligned} &2(X^2+Y^2+Z^2-XY-YZ-ZX) \\ &= (X^2-2XY+Y^2)+(Y^2-2YZ+Z^2) \\ &\qquad +(Z^2-2ZX+X^2) \\ &= (X-Y)^2+(Y-Z)^2+(Z-X)^2 \end{aligned}\] が得られる.
- (3)
- $X,$ $Y,$ $Z \geqq 0$ のとき, \[\begin{aligned} &X^3+Y^3+Z^3-3XYZ \\ &= (X+Y+Z)(X^2+Y^2+Z^2-XY-YZ-ZX) \\ &= (X+Y+Z)\frac{1}{2}\{ (X-Y)^2+(Y-Z)^2+(Z-X)^2\} \\ &\geqq 0 \end{aligned}\] が成り立つ. この不等式に $X = \sqrt[3]{x},$ $Y = \sqrt[3]{y},$ $Z = \sqrt[3]{z}$ を代入すると, 求める不等式が得られる.
問題《並べ替えと相加・相乗平均の不等式》
次のことを示せ.
- (1)
- $a \geqq b,$ $c \geqq d$ のとき, $ac+bd \geqq ad+bc$ が成り立つ.
- (2)
- $X,$ $Y \geqq 0$ のとき, $X^2+Y^2 \geqq 2XY$ が成り立つ.
- (3)
- $X,$ $Y,$ $Z \geqq 0$ のとき, $X^3+Y^3+Z^3 \geqq 3XYZ$ が成り立つ.
- (4)
- $x,$ $y,$ $z \geqq 0$ のとき, $x+y+z \geqq 3\sqrt[3]{xyz}$ が成り立つ.
解答例
- (1)
- $a \geqq b,$ $c \geqq d$ から $a-b \geqq 0,$ $c-d \geqq 0$ であるので, \[\begin{aligned} (ac+bd)-(ad+bc) &= a(c-d)-b(c-d) \\ &= (a-b)(c-d) \geqq 0 \end{aligned}\] つまり \[ ac+bd \geqq ad+bc\] が成り立つ.
- (2)
- $X \geqq Y \geqq 0$ として一般性を失わない. このとき, (1) から, \[ X^2+Y^2 \geqq XY+YX = 2XY\] が成り立つ.
- (3)
- $X \geqq Y \geqq Z \geqq 0$ として一般性を失わない. このとき, \[\begin{aligned} X^3+Y^3+Z^3 &= X^3+Y^2Y+Z^2Z \\ &\geqq X^3+Y^2Z+Z^2Y \\ &\qquad (\because Y^2 \geqq Z^2,\ Y \geqq Z,\ (1)) \\ &= X^2X+Y^2Z+ZY\cdot Z \\ &\geqq X^2Z+Y^2Z+ZYX \\ &\qquad (\because X^2 \geqq ZY,\ X \geqq Z,\ (1)) \\ &= (X^2+Y^2)Z+XYZ \\ &\geqq 2XYZ+XYZ \quad (\because (2)) \\ &= 3XYZ \end{aligned}\] つまり \[ X^3+Y^3+Z^3 \geqq 3XYZ\] が成り立つ.
- (4)
- (3) に $X = \sqrt[3]{x},$ $Y = \sqrt[3]{y},$ $Z = \sqrt[3]{z}$ を代入すると, \[ x+y+z \geqq 3\sqrt[3]{xyz}\] が得られる.
参考
- $x_1 \geqq \cdots \geqq x_n,$ $y_1 \geqq \cdots \geqq y_n,$ $\{\sigma (1),\cdots,\sigma (n)\} = \{ 1,\cdots,n\}$ のとき, 「並べ替え不等式」 (rearrangement inequality) と呼ばれる不等式 \[\sum_{k = 1}^nx_ky_{\sigma (k)} \leqq \sum_{k = 1}^nx_ky_k\] の成り立つことが知られている. これは, $x_{i1} \geqq \cdots \geqq x_{in} \geqq 0$ を満たす $m$ 個の数列 $\{ x_{ij}\}$ $(1 \leqq i \leqq m)$ と $\{\sigma _i(1),\cdots,\sigma _i(n)\} = \{ 1,\cdots,n\}$ を満たす置換 $\sigma _i$ $(1 \leqq i \leqq m)$ に対する不等式 \[\sum_{k = 1}^nx_{1\sigma _1(k)}\cdots x_{m\sigma _r(k)} \leqq \sum_{k = 1}^nx_{1k}\cdots x_{mk}\] に一般化される.
- 本問の証明は近年, 内田康晴氏によって発見された「並べ替え不等式」による相加・相乗平均の不等式 \[\frac{x_1+\cdots +x_n}{n} \geqq \sqrt[n]{x_1\cdots x_n} \quad (x_1,\ \dots,\ x_n \geqq 0)\] の証明の $n = 3$ の場合である. 一般の $n$ に対しては, 数学的帰納法で同様に証明できる (Y. Uchida, A simple proof of the geometric-arithmetic mean inequality, Pure Appl. Math. 9(2) (2008), 1–2).
- 「並べ替え不等式」から「コーシー=シュワルツの不等式」を導くこともできる.
問題《和・積の関係と相加・相乗平均の不等式》
次のことを示せ.
- (1)
- $a \leqq 1 \leqq b$ のとき \[ a+b \geqq ab+1 \quad \cdots [1]\] が成り立つ.
- (2)
- $a_1\cdots a_n = 1$ を満たす $n$ 個の正の数 $a_1,$ $\cdots,$ $a_n$ に対して \[ a_1+\cdots +a_n \geqq n \quad \cdots [2]\] が成り立つ.
- (3)
- 正の数 $x_1,$ $\cdots,$ $x_n$ に対して \[ x_1+\cdots +x_n \geqq n(x_1\cdots x_n)^{\frac{1}{n}} \quad \cdots [3]\] が成り立つ.
解答例
- (1)
- $a \leqq 1 \leqq b$ のとき, \[ (a+b)-(ab+1) \geqq (1-a)(b-1) \geqq 0\] であるから, $[1]$ が成り立つ.
- (2)
- (i)
- $n = 1$ のとき, $[2]$ は明らかに成り立つ.
- (ii)
- $n = k$ ($k$: 正の整数) のとき, $[2]$ が成り立つとして, $n = k+1$ の場合を考える. $a_k \leqq 1 \leqq a_{k+1}$ としても一般性を失わない. このとき, $[1]$ から, \[\begin{aligned} a_1+\cdots +a_k+a_{k+1} &\geqq a_1+\cdots +a_ka_{k+1}+1 \\ &\geqq k+1 \end{aligned}\] が成り立つ. 第 $2$ の不等号は, $a_1\cdots a_{k-1}(a_ka_{k+1}) = 1$ であることから従う.
- (3)
- $G_n = (x_1\cdots x_n)^{\frac{1}{n}},$ $a_k = \dfrac{x_k}{G_n}$ とおくと, $a_1\cdots a_n = 1$ となるから, $[2]$ により, \[\begin{aligned} \frac{x_1}{G_n}+\cdots +\frac{x_n}{G_n} &\geqq n \\ x_1+\cdots +x_n &\geqq nG_n \end{aligned}\] つまり $[3]$ が成り立つ.
参考
相加・相乗平均の不等式のその他の証明については, こちらも参照されたい.
問題《レームスの不等式とオイラーの不等式》
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $S = \triangle\mathrm{ABC}$ とおき, 外接円の半径を $R,$ 内接円の半径を $r$ とおく.
- (1)
- 不等式 \[ abc \geqq (-a+b+c)(a-b+c)(a+b-c)\] が成り立つことを, \[ x = -a+b+c, \quad y = a-b+c, \quad z = a+b-c\] という置き換えを使って示せ.
- (2)
- 不等式 \[ R \geqq 2r\] が成り立つことを示せ. ただし,「ヘロンの公式」 \[ S = \dfrac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}\] (こちらを参照) が成り立つことは, 証明なしに使ってよい.
解答例
- (1)
- $x = -a+b+c,$ $y = a-b+c,$ $z = a+b-c$ とおく. このとき, \[ a = \frac{y+z}{2}, \quad b = \frac{z+x}{2}, \quad c= \frac{x+y}{2}\] となる. $a,$ $b,$ $c$ は三角形の $3$ 辺の長さであるから $x,$ $y,$ $z > 0$ であることに注意すると, 相加・相乗平均の不等式により \[\begin{aligned} abc &= \frac{y+z}{2}\cdot\frac{z+x}{2}\cdot\frac{x+y}{2} \\ &\geqq \sqrt{yz}\sqrt{zx}\sqrt{xy} = xyz \\ &= (-a+b+c)(a-b+c)(a+b-c) \quad \cdots [1] \end{aligned}\] が得られる. 等号成立は, $x = y = z$ つまり $a = b = c$ の場合に限る.
- (2)
- 正弦定理により,
$S = \dfrac{1}{2}bc\sin\angle\mathrm A = \dfrac{abc}{4R}$ つまり $abc = 4RS \quad \cdots [2]$が成り立つ. また,「ヘロンの公式」により, \[ (-a+b+c)(a-b+c)(a+b-c) = \frac{16S^2}{a+b+c} \quad \cdots [3]\] が成り立つ. $[2],$ $[3]$ を $[1]$ に代入すると, $S = \dfrac{a+b+c}{2}r$ により, \[ 4RS \geqq \frac{16S^2}{a+b+c} = 16S\cdot\frac{r}{2} = 8rS\] つまり $R \geqq 2r$ が得られる. 等号成立は, $a = b = c$ の場合に限る.
参考
(1) の不等式は「レームスの不等式」(Lehmus inequality, 別証明はこちらを参照), (2) の不等式は「オイラーの不等式」(Euler's inequality) として知られている.
「オイラーの不等式」は, 三角形の外心と内心の距離に関する「チャップル=オイラーの定理」(Chapple–Euler theorem, こちらを参照)に一般化される.
コーシー=シュワルツの不等式
問題《コーシー=シュワルツの不等式と三角形の類似重心の特徴付け》
- (A)
- $a,$ $b,$ $c,$ $x,$ $y,$ $z$ を正の数とする. \[ (ax+by+cz)^2 \leqq (a^2+b^2+c^2)(x^2+y^2+z^2)\] が成り立ち, 等号成立は $x:y:z = a:b:c$ のときに限ることを示せ.
- (B)
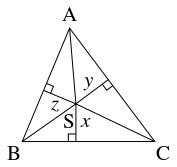
- $\triangle\mathrm{ABC}$ において, 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の中点をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおき, $\angle\mathrm A,$ $\angle\mathrm B,$ $\angle\mathrm C$ の二等分線に関して中線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ と対称な直線と辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の交点をそれぞれ $\mathrm P',$ $\mathrm Q',$ $\mathrm R'$ とおく.
さらに, $\mathrm S$ を $\triangle\mathrm{ABC}$ の頂点と異なる周上または内部の点とし, 点 $\mathrm S$ と直線 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の距離を $x,$ $y,$ $z$ とおく.
また, $a =\mathrm{BC},$ $b =\mathrm{CA},$ $c =\mathrm{AB}$ とおく.
次のことを示せ.
- (1)
- 点 $\mathrm S$ が直線 $\mathrm{AP}'$ 上にあるとき, $y:z = b:c$ が成り立つ.
- (2)
- $\mathrm{BP}':\mathrm{CP}' = c^2:b^2$ が成り立つ.
- (3)
- $3$ 本の直線 $\mathrm{AP}',$ $\mathrm{BQ}',$ $\mathrm{CR}'$ は $1$ 点で交わる.
- (4)
- $x^2+y^2+z^2$ が最小であるとき, $x:y:z = a:b:c$ が成り立ち, $\mathrm S$ は (3) の点に一致する.
解答例
- (A)
- 右辺から左辺を引くと \[\begin{aligned} &(a^2+b^2+c^2)(x^2+y^2+z^2)-(ax+by+cz)^2 \\ &= (a^2y^2-2abxy+b^2x^2)+(b^2z^2-2bcyz+c^2y^2) \\ &\qquad\qquad\qquad\qquad\qquad\quad +(c^2x^2-2cazx+a^2z^2) \\ &= (ay-bx)^2+(bz-cy)^2+(cx-az)^2 \\ &\geqq 0 \end{aligned}\] となるから, \[ (ax+by+cz)^2 \leqq (a^2+b^2+c^2)(x^2+y^2+z^2)\] が成り立つ. 等号成立は, $ay-bx = bz-cy = cx-az,$ つまり $a:b:c = x:y:z$ のときに限る.
- (B)
- (1)
- 点 $\mathrm S,$ および点 $\mathrm P$ から辺 $\mathrm{CA},$ $\mathrm{AB}$ に下ろした垂線の足をそれぞれ $\mathrm S_2,$ $\mathrm S_3,$ および $\mathrm P_2,$ $\mathrm P_3$ とおく.
このとき,
\[\angle\mathrm P_3\mathrm{AP} = \angle\mathrm S_2\mathrm{AS}, \quad \angle\mathrm P_2\mathrm{AP} = \angle\mathrm S_3\mathrm{AS}\]
となるから, 直角三角形 $\mathrm P_3\mathrm{AP}$ と $\mathrm S_2\mathrm{AS},$ $\mathrm P_2\mathrm{AP}$ と $\mathrm S_3\mathrm{AS}$ はそれぞれ相似である.
よって, \[\frac{\mathrm{SS}_2}{\mathrm{AS}} = \frac{\mathrm{PP}_3}{\mathrm{AP}}, \quad \frac{\mathrm{SS}_3}{\mathrm{AS}} = \frac{\mathrm{PP}_2}{\mathrm{AP}}\] から, \[\begin{aligned} y:z &= \mathrm{SS}_2:\mathrm{SS}_3 = \mathrm{PP}_3:\mathrm{PP}_2 = \frac{2\triangle\mathrm{ABP}}{c}:\frac{2\triangle\mathrm{ACP}}{b} \\ &= b:c \quad (\because\mathrm{BP} = \mathrm{CP}) \end{aligned}\] が成り立つ.
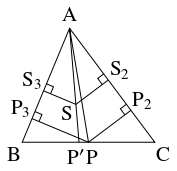
- (2)
- (1) において $\mathrm S = \mathrm P'$ とすると $y:z = b:c$ となるから, \[\mathrm{BP}':\mathrm{CP}' = \triangle\mathrm{ABP}':\triangle\mathrm{ACP}' = \frac{1}{2}cz:\frac{1}{2}by = c^2:b^2\] が成り立つ.
- (3)
- (2) により \[\begin{aligned} \frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{BP}'}{\mathrm P'\mathrm C} &= \frac{\mathrm{AB}^2}{\mathrm{AC}^2} \quad \cdots [1], \\ \frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{CQ}'}{\mathrm Q'\mathrm A} &= \frac{\mathrm{BC}^2}{\mathrm{BA}^2} \quad \cdots [2], \\ \frac{\mathrm{AR}}{\mathrm{RB}}\cdot\frac{\mathrm{AR}'}{\mathrm R'\mathrm B} &= \frac{\mathrm{CA}^2}{\mathrm{CB}^2} \quad \cdots [3] \end{aligned}\] が成り立つ. また, $\triangle\mathrm{ABC}$ の $3$ 本の中線が $1$ 点で交わることとチェヴァの定理により \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1\] であるから, $[1]$~$[3]$ の辺々を掛け合わせると \[\frac{\mathrm{BP}'}{\mathrm P'\mathrm C}\cdot\frac{\mathrm{CQ}'}{\mathrm Q'\mathrm A}\cdot\frac{\mathrm{AR}'}{\mathrm R'\mathrm B} = 1\] が得られる. ゆえに, チェヴァの定理の逆により, $3$ 本の直線 $\mathrm{AP}',$ $\mathrm{BQ}',$ $\mathrm{CR}'$ は $1$ 点で交わる.
- (4)
- $\triangle\mathrm{ABC}$ を $\triangle\mathrm{SBC},$ $\triangle\mathrm{SCA},$ $\triangle\mathrm{SAB}$ に分けると
\[\triangle\mathrm{ABC} = \frac{ax}{2}+\frac{by}{2}+\frac{cz}{2} = \frac{ax+by+cz}{2}\]
であることがわかるから,
\[ ax+by+cz = 2\triangle\mathrm{ABC}\]
が成り立つ.
これと (A) の不等式をあわせると, \[ x^2+y^2+z^2 \geqq \frac{(ax+by+cz)^2}{a^2+b^2+c^2} = \frac{4(\triangle\mathrm{ABC})^2}{a^2+b^2+c^2}\] が得られる (等号成立は $x:y:z = a:b:c$ のときに限る). よって, $x^2+y^2+z^2$ の値が最小であるとき, $x:y:z = a:b:c$ である. このとき, \[\triangle\mathrm{SBC}:\triangle\mathrm{SCA}:\triangle\mathrm{SAB} = a^2:b^2:c^2\] であり, 直線 $\mathrm{AS}$ は辺 $\mathrm{BC}$ を $c^2:b^2$ に, 直線 $\mathrm{BS}$ は辺 $\mathrm{CA}$ を $a^2:c^2$ に, 直線 $\mathrm{CS}$ は辺 $\mathrm{AB}$ を $b^2:a^2$ に内分するから, $\mathrm S$ は (3) の点に一致する.
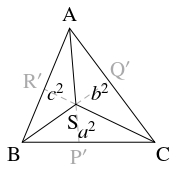
参考
- (A) の不等式は「コーシー=シュワルツの不等式」(Cauchy–Schwarz inequality) の特別な場合である.
- 三角形において, 角の頂点を通る直線 $l,$ $l'$ がその角の二等分線に関して対称であるとき, $l,$ $l'$ は互いに「等角共役線」(isogonal conjugate line) であるという. 特に, 三角形の中線の「等角共役線」を「類似中線」(symmedian) と呼ぶ (作図法についてはこちらを参照).
- $\triangle\mathrm{ABC}$ において, $3$ 本の「類似中線」の交点を「類似重心」または「ルモワーヌ点」(Lemoine point) と呼ぶ. これは重心の「等角共役点」である.
問題《ラグランジュの恒等式とコーシー=シュワルツの不等式》
$n$ を $2$ 以上の整数, $x_1,$ $\cdots,$ $x_n,$ $y_1,$ $\cdots,$ $y_n$ を実数とする.
「ラグランジュの恒等式」
\[\left(\sum_{k = 1}^nx_k{}^2\right)\left(\sum_{k = 1}^ny_k{}^2\right) = \left(\sum_{k = 1}^nx_ky_k\right) ^2+\sum_{k = 1}^{n-1}\sum_{l = k+1}^n(x_ky_l-x_ly_k)^2\]
(こちらを参照) を使って, 不等式
\[\left(\sum_{k = 1}^nx_k{}^2\right)\left(\sum_{k = 1}^ny_k{}^2\right) \geqq \left(\sum_{k = 1}^nx_ky_k\right) ^2\]
が成り立つことを示せ.
また, 等号成立条件を求めよ.
解答例
「ラグランジュの恒等式」
\[\left(\sum_{k = 1}^nx_k{}^2\right)\left(\sum_{k = 1}^ny_k{}^2\right) = \left(\sum_{k = 1}^nx_ky_k\right) ^2+\sum_{k = 1}^{n-1}\sum_{l = k+1}^n(x_ky_l-x_ly_k)^2\]
において $(x_ky_l-x_ly_k)^2 \geqq 0$ $(1 \leqq k \leqq n-1,$ $k+1 \leqq l \leqq n)$ であるから,
\[\left(\sum_{k = 1}^nx_k{}^2\right)\left(\sum_{k = 1}^ny_k{}^2\right) \geqq \left(\sum_{k = 1}^nx_ky_k\right) ^2\]
が成り立つ.
等号成立は
\[ x_ky_l = x_ly_k \quad (1 \leqq k \leqq n-1,\ k+1 \leqq l \leqq n) \quad \cdots [1]\]
の場合に限る.
この条件のもとで, $(x_1,\cdots,x_n),$ $(y_1,\cdots,y_n) \neq (0,\cdots,0)$ であるとする. このとき, ある番号 $k,$ $l$ について $x_k,$ $y_l \neq 0$ となる. $x_ly_k = x_ky_l \neq 0$ から, $y_k \neq 0$ であることに注意する. $t = \dfrac{y_k}{x_k}$ とおく.
明らかに $[2] \Longrightarrow [1]$ も成り立つから, 等号成立は \[\begin{aligned} (x_1,\cdots,x_n) &= (0,\cdots,0) \quad\text{または} \\ (y_1,\cdots,y_n) &= (tx_1,\cdots,tx_n) \quad (t\text{: 実数}) \end{aligned}\] の場合に限る.
この条件のもとで, $(x_1,\cdots,x_n),$ $(y_1,\cdots,y_n) \neq (0,\cdots,0)$ であるとする. このとき, ある番号 $k,$ $l$ について $x_k,$ $y_l \neq 0$ となる. $x_ly_k = x_ky_l \neq 0$ から, $y_k \neq 0$ であることに注意する. $t = \dfrac{y_k}{x_k}$ とおく.
- (i)
- $j = k$ のとき. $y_j = tx_j$ となる.
- (ii)
- $j \neq k,$ $x_jy_k = x_ky_j \neq 0$ のとき. $x_j \neq 0,$ $\dfrac{y_j}{x_j} = \dfrac{y_k}{x_k} = t$ から $y_j = tx_j$ となる.
- (iii)
- $j \neq k,$ $x_jy_k = x_ky_j = 0$ のとき. $x_jy_k = 0,$ $y_k \neq 0$ から $x_j = 0$ となり, $x_ky_j = 0,$ $x_k \neq 0$ から $y_j = 0$ となるので, $y_j = tx_j$ となる.
明らかに $[2] \Longrightarrow [1]$ も成り立つから, 等号成立は \[\begin{aligned} (x_1,\cdots,x_n) &= (0,\cdots,0) \quad\text{または} \\ (y_1,\cdots,y_n) &= (tx_1,\cdots,tx_n) \quad (t\text{: 実数}) \end{aligned}\] の場合に限る.
参考
- 本問で示した不等式は「コーシー=シュワルツの不等式」(Cauchy–Schwarz inequality) と呼ばれる.
- 別証明については, こちらを参照されたい.
三角不等式
$A \geqq 0,$ $B \geqq 0$ であるとき, 不等式 $A \geqq B$ を示すには, $A^2 \geqq B^2$ を示すことがしばしば有効である.
問題《三角不等式とマンハッタン距離》
次のことを示せ.
- (1)
- すべての実数 $x,$ $y$ に対して, $|x|+|y| \geqq |x+y|$ が成り立つ.
- (2)
- 平面上の $2$ 点 $\mathrm P(x,y),$ $\mathrm P'(x',y')$ に対して, \[ d(\mathrm P,\mathrm P') = |x'-x|+|y'-y|\] と定める. このとき, $3$ 点 $\mathrm P,$ $\mathrm P',$ $\mathrm P''$ に対して, \[ d(\mathrm P,\mathrm P')+d(\mathrm P',\mathrm P'') \geqq d(\mathrm P,\mathrm P'')\] が成り立つ.
解答例
- (1)
- \[\begin{aligned} &(|x|+|y|)^2-|x+y|^2 \\ &= (|x|^2+2|x||y|+|y|^2)-(x+y)^2 \\ &= (x^2+2|xy|+y^2)-(x^2+2xy+y^2) \\ &= 2(|xy|-xy) \geqq 0 \end{aligned}\] から $(|x|+|y|)^2 \geqq |x+y|^2$ であるので, $|x|+|y| \geqq 0,$ $|x+y| \geqq 0$ に注意すると \[ |x|+|y| \geqq |x+y|\] が得られる.
- (2)
- $\mathrm P(x,y),$ $\mathrm P'(x',y'),$ $\mathrm P''(x'',y'')$ とおく. このとき, (1) で示した不等式により, \[\begin{aligned} &d(\mathrm P,\mathrm P')+d(\mathrm P',\mathrm P'') \\ &= (|x'-x|+|y'-y|)+(|x''-x'|+|y''-y'|) \\ &= (|x''-x'|+|x'-x|)+(|y''-y'|+|y'-y|) \\ &\geqq |(x''-x')+(x'-x)|+|(y''-y')+(y'-y)| \\ &= |x''-x|+|y''-y| \\ &= d(\mathrm P,\mathrm P'') \end{aligned}\] が成り立つ.
参考
- 不等式 $|x|+|y| \geqq |x+y|$ は「三角不等式」(triangle inequality) と呼ばれる.
- 平面上の $2$ 点 $\mathrm P(x,y),$ $\mathrm P'(x',y')$ に対して,
\[ d(\mathrm P,\mathrm P') = |x'-x|+|y'-y|\]
を $\mathrm P,$ $\mathrm P'$ の「マンハッタン距離」(Manhattan distance) と呼ぶ.
この概念は, 碁盤目状に道路が整備された街で $2$ 点がどれだけ離れているかを考える際に有効である.
例えば, 点 $\mathrm A(3,4)$ は原点を中心とする半径 $5$ の円周上にあり, 点 $\mathrm B(1,5)$ はその円の外側にあるが,
原点と点 $\mathrm A$ の「マンハッタン距離」は $3+4 = 7,$ 原点と点 $\mathrm B$ の「マンハッタン距離」は $1+5 = 6$ であり,
「マンハッタン距離」では点 $\mathrm A$ よりも点 $\mathrm B$ の方が原点に近い.
我々が日常的に距離と呼んでいる「ユークリッド距離」(Euclidean distance) と「マンハッタン距離」は, 次の共通の性質をもつ.
- (D1)
- $d(\mathrm P,\mathrm P') \geqq 0$ であり, $d(\mathrm P,\mathrm P') = 0$ $\iff$ $\mathrm P = \mathrm P'$ が成り立つ.
- (D2)
- $d(\mathrm P,\mathrm P') = d(\mathrm P',\mathrm P)$ が成り立つ.
- (D3)
- $d(\mathrm P,\mathrm P')+d(\mathrm P',\mathrm P'') \geqq d(\mathrm P,\mathrm P'')$ が成り立つ.
問題《三角不等式と高次方程式の解の評価》
-
$a_0,$ $a_1,$ $\cdots,$ $a_{n-1}$ $(n \geqq 1)$ を実数とし, それらの絶対値の最大値を $M$ とおく.
方程式
\[ x^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0 = 0\]
の実数解 $\alpha\,(\neq 0)$ が存在するとき, $|\alpha | \leqq M+1$ が成り立つことを, 前問で示した不等式 $|x+y| \leqq |x|+|y|$ を使って, 背理法で示せ.
解答例
$x^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0 = 0$ が実数解 $\alpha\,(\neq 0)$ をもつとする.
このとき,
\[\begin{aligned}
\alpha ^n+a_{n-1}\alpha ^{n-1}+\cdots +a_1\alpha +a_0 &= 0 \\
\alpha +a_{n-1}+\cdots +\frac{a_1}{\alpha ^{n-2}}+\frac{a_0}{\alpha ^{n-1}} &= 0 \quad \cdots [1]
\end{aligned}\]
が成り立つ.
仮に $|\alpha | > M+1$ が成り立つとすると, \[\frac{1}{|\alpha |} < \frac{1}{M+1} \quad \cdots [2]\] となるから, \[\begin{aligned} |\alpha | &= \left| a_{n-1}+\cdots +\frac{a_1}{\alpha ^{n-2}}+\frac{a_0}{\alpha ^{n-1}}\right| \quad (\because [1]) \\ &\leqq |a_{n-1}|+\cdots +\left|\frac{a_1}{\alpha ^{n-2}}\right| +\left|\frac{a_0}{\alpha ^{n-1}}\right| \\ &= |a_{n-1}|+\cdots +\frac{|a_1|}{|\alpha |^{n-2}}+\frac{|a_0|}{|\alpha |^{n-1}} \\ &\leqq M\left( 1+\cdots +\frac{1}{|\alpha |^{n-2}}+\frac{1}{|\alpha |^{n-1}}\right) \quad (\because |a_k| \leqq M) \\ &< M\left\{ 1+\cdots +\frac{1}{(M+1)^{n-2}}+\frac{1}{(M+1)^{n-1}}\right\} \quad (\because [2]) \\ &= M\cdot\!\frac{1-\left(\dfrac{1}{M+1}\right) ^n}{1-\dfrac{1}{M+1}} = M\cdot\frac{(M+1)^n-1}{(M+1)^n-(M+1)^{n-1}} \\ &= M\cdot\frac{(M+1)^n-1}{(M+1)^{n-1}(M+1-1)} = \frac{(M+1)^n-1}{(M+1)^{n-1}} \\ &< \frac{(M+1)^n}{(M+1)^{n-1}} = M+1 \end{aligned}\] となって, 矛盾が生じる.
ゆえに, $|\alpha | \leqq M+1$ が成り立つ.
仮に $|\alpha | > M+1$ が成り立つとすると, \[\frac{1}{|\alpha |} < \frac{1}{M+1} \quad \cdots [2]\] となるから, \[\begin{aligned} |\alpha | &= \left| a_{n-1}+\cdots +\frac{a_1}{\alpha ^{n-2}}+\frac{a_0}{\alpha ^{n-1}}\right| \quad (\because [1]) \\ &\leqq |a_{n-1}|+\cdots +\left|\frac{a_1}{\alpha ^{n-2}}\right| +\left|\frac{a_0}{\alpha ^{n-1}}\right| \\ &= |a_{n-1}|+\cdots +\frac{|a_1|}{|\alpha |^{n-2}}+\frac{|a_0|}{|\alpha |^{n-1}} \\ &\leqq M\left( 1+\cdots +\frac{1}{|\alpha |^{n-2}}+\frac{1}{|\alpha |^{n-1}}\right) \quad (\because |a_k| \leqq M) \\ &< M\left\{ 1+\cdots +\frac{1}{(M+1)^{n-2}}+\frac{1}{(M+1)^{n-1}}\right\} \quad (\because [2]) \\ &= M\cdot\!\frac{1-\left(\dfrac{1}{M+1}\right) ^n}{1-\dfrac{1}{M+1}} = M\cdot\frac{(M+1)^n-1}{(M+1)^n-(M+1)^{n-1}} \\ &= M\cdot\frac{(M+1)^n-1}{(M+1)^{n-1}(M+1-1)} = \frac{(M+1)^n-1}{(M+1)^{n-1}} \\ &< \frac{(M+1)^n}{(M+1)^{n-1}} = M+1 \end{aligned}\] となって, 矛盾が生じる.
ゆえに, $|\alpha | \leqq M+1$ が成り立つ.
参考
高次方程式の解の評価については「エネストレーム=掛谷の定理」(こちらを参照) が有名である.
いろいろな不等式
問題《$2$ 乗平均平方根と相加平均の関係》
$n$ を $2$ 以上の整数, $x_1,$ $\cdots,$ $x_n$ を正の数とし,
\[ r = \sqrt{\frac{x_1{}^2+\cdots +x_n{}^2}{n}}, \quad m = \frac{x_1+\cdots +x_n}{n}\]
とおく.
\[\frac{(x_1-m)^2+\cdots +(x_n-m)^2}{n} = r^2-m^2\]
を示すことで,
\[ r \geqq m\]
が成り立つことを示せ.
また, 等号成立条件を求めよ.
解答例
\[\begin{aligned}
\frac{1}{n}\sum_{k = 1}^n(x_k-m)^2 &= \frac{1}{n}\sum_{k = 1}^n(x_k{}^2-2mx_k+m^2) \\
&= \frac{1}{n}\sum_{k = 1}^nx_k{}^2-2m\cdot\frac{1}{n}\sum_{k = 1}^nx_k+\frac{1}{n}\cdot nm^2 \\
&= r^2-2m\cdot m+m^2 = r^2-m^2
\end{aligned}\]
であるから,
\[ r^2-m^2 = \frac{1}{n}\sum_{k = 1}^n(x_k-m)^2 \geqq 0\]
が成り立つ.
ゆえに, $r^2 \geqq m^2$ つまり
\[ r \geqq m\]
が成り立つ.
等号成立は, $x_1-m = \cdots = x_n-m = 0$ つまり
\[ x_1 = \cdots = x_n\]
の場合に限る.
参考
- $\sqrt{\dfrac{x_1{}^2+\cdots +x_n{}^2}{n}}$ は $x_1,$ $\cdots,$ $x_n$ の 「$2$ 乗平均平方根」と呼ばれ, 統計学, 物理学, 工学で重要な応用をもつ.
- $x_1,$ $\cdots,$ $x_n$ の「$2$ 乗平均平方根」, 相加平均, 相乗平均,「調和平均」は,「一般化平均」または「ヘルダー平均」と呼ばれる代表値 \[ M_p(x_1,\cdots,x_n) = \left(\frac{1}{n}\sum_{k = 1}^nx_k{}^p\right) ^{\frac{1}{p}}\] ($p$: 実数) の特別な場合, つまり $p = 2,$ $1,$ $0,$ $-1$ の場合である ($p = 0$ の場合は $p \to 0$ のときの極限とみなすと相乗平均になる). 一般に, $p > q$ のとき \[ M_p(x_1,\cdots,x_n) \geqq M_q(x_1,\cdots,x_n)\] の成り立つことが知られている.
問題《アルキメデスの開平法》
正の整数 $a,$ $b$ が $b < 2a-1$ を満たすとき,
\[ a^2-b > a^2-(2a-1) = (a-1)^2 \geqq 0\]
である.
このとき,
\[ a-\frac{b}{2a-1} < \sqrt{a^2-b} < a-\frac{b}{2a}\]
が成り立つことを示せ.
解答例
- $2a\sqrt{a^2-b} > 0$ であるから, $\sqrt{a^2-b} < a-\dfrac{b}{2a}$ つまり $2a\sqrt{a^2-b} < 2a^2-b$ を示すには, $4a^2(a^2-b) < (2a^2-b)^2$ を示せばよい. これは, \[\begin{aligned} &(2a^2-b)^2-4a^2(a^2-b) \\ &= (4a^4-4a^2b+b^2)-(4a^4-4a^2b) \\ &= b^2 > 0 \end{aligned}\] から成り立つ.
- $(2a-1)a-b > ba-b = b(a-1) \geqq 0$ であるから, $a-\dfrac{b}{2a-1} < \sqrt{a^2-b}$ つまり $(2a-1)a-b < (2a-1)\sqrt{a^2-b}$ を示すには, $\{ (2a-1)a-b\} ^2 < (2a-1)^2(a^2-b)$ を示せばよい. これは, \[\begin{aligned} &(2a-1)^2(a^2-b)-\{ (2a-1)a-b\} ^2 \\ &= (2a-1)^2(a^2-b)-(2a-1)^2a^2+2(2a-1)ab-b^2 \\ &= -4a^2b+4ab-b+4a^2b-2ab-b^2 \\ &= 2ab-b-b^2 \\ &= b(2a-1-b) > 0 \end{aligned}\] から成り立つ.
参考
- アルキメデスは $a,$ $b > 0,$ $b < 2a\pm 1$ のとき \[ a\pm\frac{b}{2a\pm 1} < \sqrt{a^2\pm b} < a\pm\frac{b}{2a}\] (複号同順) が成り立つことを使って, 平方根の近似値を求めていたと考えられている.
- 例えば, $\sqrt 3$ の近似値は, 次のように求めることができる. $3 = 2^2-1$ から, \[\frac{5}{3} = 2-\frac{1}{2\cdot 2-1} < \sqrt 3 < 2-\frac{1}{2\cdot 2} = \frac{7}{4}\] よって $\dfrac{20}{3} < 4\sqrt 3 < 7$ が成り立つ. したがって, $4\sqrt 3 = \sqrt{48}$ に最も近い整数は $7$ であることが見出せる. $48 = 7^2-1$ から, \[\frac{90}{13} = 7-\frac{1}{2\cdot 7-1} < 4\sqrt 3 < 7-\frac{1}{2\cdot 7} = \frac{97}{14}\] よって $\dfrac{1260}{13} < 56\sqrt 3 < 97$ が成り立つ. したがって, $56\sqrt 3 = \sqrt{9408}$ に最も近い整数は $97$ であるであることが見出せる. $9408 = 97^2-1$ から, \[\frac{18720}{193} = 97-\frac{1}{2\cdot 97-1} < 56\sqrt 3 < 97-\frac{1}{2\cdot 97} = \frac{18817}{194}\] よって $\dfrac{2340}{1351} < \sqrt 3 < \dfrac{18817}{10864}$ が成り立つ. \[\frac{2340}{1351} = 1.7320503\cdots, \quad \frac{18817}{10864} = 1.7320508\cdots\] であるから, $\sqrt 3$ の近似値を小数第 $6$ 位まで求めることができた.
問題《チェビシェフの和の不等式》
$x_1 \geqq \cdots \geqq x_n,$ $y_1 \geqq \cdots \geqq y_n$ のとき, 不等式
\[\frac{1}{n}\sum_{k = 1}^nx_ky_k \geqq \left(\frac{1}{n}\sum_{k = 1}^nx_k\right)\left(\frac{1}{n}\sum_{k = 1}^ny_k\right)\]
が成り立つことを示せ.
(参考: $1992$ 東北大)
解答例
$x_1 \geqq \cdots \geqq x_n,$ $y_1 \geqq \cdots \geqq y_n$ のとき,
$x_k-x_l,$ $y_k-y_l$ は同符号であるから
\[\begin{aligned}
0 &\leqq \sum_{k = 1}^n\sum_{l = 1}^n(x_k-x_l)(y_k-y_l) \quad \cdots [1] \\
&= \sum_{k = 1}^n\sum_{l = 1}^n(x_ky_k-x_ky_l-x_ly_k+x_ly_l) \\
&= \sum_{k = 1}^n\left( nx_ky_k-x_k\sum_{l = 1}^ny_l-y_k\sum_{l = 1}^nx_l+\sum_{l = 1}^nx_ly_l\right) \\
&= n\sum_{k = 1}^nx_ky_k-\sum_{k = 1}^nx_k\sum_{l = 1}^ny_l-\sum_{k = 1}^ny_k\sum_{l = 1}^nx_l+n\sum_{l = 1}^nx_ly_l \\
&= 2n\sum_{k = 1}^nx_ky_k-2\left(\sum_{k = 1}^nx_k\right)\left(\sum_{k = 1}^ny_k\right)
\end{aligned}\]
つまり
\[ 2n\sum_{k = 1}^nx_ky_k \geqq 2\left(\sum_{k = 1}^nx_k\right)\left(\sum_{k = 1}^ny_k\right)\]
が成り立ち, 両辺を $2n^2$ で割ると
\[\frac{1}{n}\sum_{k = 1}^nx_ky_k \geqq \left(\frac{1}{n}\sum_{k = 1}^nx_k\right)\left(\frac{1}{n}\sum_{k = 1}^ny_k\right)\]
が得られる.
参考
- 本問の不等式は, $x_1 \geqq \cdots \geqq x_n,$ $y_1 \geqq \cdots \geqq y_n,$ $\{\sigma (1),\cdots,\sigma (n)\} = \{ 1,\cdots,n\}$ のときに成り立つ「並べ替え不等式」 \[\sum_{k = 1}^nx_ky_k \geqq \sum_{k = 1}^nx_ky_{\sigma (k)}\] において $\sigma (k) = k+l-1$ ($l$: $1 \leqq l \leqq n$ なる整数, $k+l-1 > n$ のとき $y_{k+l-1} = y_{k+l-1-n}$ とおく) として得られる $n$ 個の不等式について辺々の和をとり, 両辺を $n^2$ で割ることでも証明できる.
- これは, \[\begin{aligned} \frac{1}{n}\sum_{k = 1}^nx_ky_k \leqq \left(\frac{1}{n}\sum_{k = 1}^nx_k\right)\left(\frac{1}{n}\sum_{k = 1}^ny_k\right) \\ (x_1 \geqq \cdots \geqq x_n,\ y_1 \leqq \cdots \leqq y_n) \end{aligned}\] (証明は同様) とあわせて, 「チェビシェフの和の不等式」(Chebyshev's sum inequality) として知られている.
- 本問の不等式は, $mn$ 個の変数 $x_{11},$ $\cdots,$ $x_{1n},$ $\cdots,$ $x_{m1},$ $\cdots,$ $x_{mn}$ に関する不等式 \[\begin{aligned} \frac{1}{n}\sum_{k = 1}^nx_{1k}\cdots x_{mk} \geqq \left(\frac{1}{n}\sum_{k = 1}^nx_{1k}\right)\cdots\left(\frac{1}{n}\sum_{k = 1}^nx_{mk}\right) \\ (x_{11} \geqq \cdots \geqq x_{1n},\ \cdots,\ x_{m1} \geqq \cdots \geqq x_{mn}) \end{aligned}\] に一般化される.
- 本問の不等式は, 閉区間 $[0,1]$ でともに単調増加または単調減少な実数値関数 $f(x),$ $g(x)$ に関する不等式 \[\int_0^1f(x)g(x)\,dx \geqq \left(\int_0^1f(x)\,dx\right)\left(\int_0^1g(x)\,dx\right)\] に一般化される.
問題《シューアの不等式》
すべての実数 $r$ に対して, $x,$ $y,$ $z \geqq 0$ のとき
\[\begin{aligned}
x^r(x-y)(x-z)&+y^r(y-z)(y-x) \\
&+z^r(z-x)(z-y) \geqq 0 \quad \cdots [*]
\end{aligned}\]
が成り立つことを, 次の場合に分けて示せ.
- (i)
- $r \geqq 0$ のとき.
- (ii)
- $r < 0$ のとき.
解答例
$x,$ $y,$ $z \geqq 0$ を仮定する.
$[\ast ]$ の左辺は $x,$ $y,$ $z$ に関して対称であることから $x \geqq y \geqq z$ としても一般性を失わないので, その場合を考える.
- (i)
- $r \geqq 0$ のとき. $z^r \geqq 0,$ $z-x \leqq 0,$ $z-y \leqq 0$ から, \[ z^r(z-x)(z-y) \geqq 0 \quad \cdots [1]\] が成り立つ. また, $x^r \geqq y^r\,(\geqq 0),$ $x-z \geqq y-z\,(\geqq 0)$ から \[\begin{aligned} &x^r(x-z) \geqq y^r(y-z) \\ &x^r(x-z)-y^r(y-z) \geqq 0 \end{aligned}\] であり, $x-y \geqq 0$ であるので, \[\begin{aligned} &x^r(x-y)(x-z)+y^r(y-z)(y-x) \\ &= (x-y)\{ x^r(x-z)-y^r(y-z)\} \geqq 0 \quad \cdots [2] \end{aligned}\] が成り立つ. $[1],$ $[2]$ の辺々を加えると, $[\ast ]$ が得られる.
- (ii)
- $r < 0$ のとき. $x^r \geqq 0,$ $x-y \geqq 0,$ $x-z \geqq 0$ から, \[ x^r(x-y)(x-z) \geqq 0 \quad \cdots [3]\] が成り立つ. また, $z^r \geqq y^r\,(\geqq 0),$ $x-z \geqq x-y\,(\geqq 0)$ から \[\begin{aligned} &z^r(x-z) \geqq y^r(x-y) \\ &z^r(x-z)-y^r(x-y) \geqq 0 \end{aligned}\] であり, $y-z \geqq 0$ であるので, \[\begin{aligned} &y^r(y-z)(y-x)+z^r(z-x)(z-y) \\ &= (y-z)\{ z^r(x-z)-y^r(x-y)\} \geqq 0 \quad \cdots [4] \end{aligned}\] が成り立つ. $[3],$ $[4]$ の辺々を加えると, $[\ast ]$ が得られる.
参考
- 本問で示した不等式は「シューアの不等式」(Schur's inequality) として知られている.
- $3$ 辺の長さが $a,$ $b,$ $c$ の三角形について, \[\begin{aligned} &abc-(-a+b+c)(a-b+c)(a+b-c) \\ &= a(a-b)(a-c)+b(b-c)(b-a)+c(c-a)(c-b) \\ &\geqq 0 \end{aligned}\] であるから,「レームスの不等式」(Lehmus inequality) \[ abc \geqq (-a+b+c)(a-b+c)(a+b-c)\] が成り立つ (こちらを参照).
問題《ネスビットの不等式》
$x,$ $y,$ $z$ を正の数とする.
\[\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y} \geqq \frac{3}{2}\]
が成り立つことを示せ.
- 置き換え \[ a = \frac{y+z}{2}, \quad b = \frac{z+x}{2}, \quad c = \frac{x+y}{2}\]
- $2$ 変数の相加・相乗平均の不等式: $a,$ $b \geqq 0$ ならば \[\frac{a+b}{2} \geqq \sqrt{ab}\]
- $3$ 変数の相加・相乗平均の不等式: $a,$ $b,$ $c \geqq 0$ ならば \[\frac{a+b+c}{3} \geqq \sqrt[3]{abc}\]
- 「並べ替え不等式」: $a_1 \geqq a_2 \geqq a_3,$ $b_1 \geqq b_2 \geqq b_3,$ $\{ i,j,k\} = \{ 1,2,3\}$ ならば \[ a_1b_1+a_2b_2+a_3b_3 \geqq a_1b_i+a_2b_j+a_3b_k\]
- 「チェビシェフの和の不等式」: $a_1 \geqq a_2 \geqq a_3,$ $b_1 \geqq b_2 \geqq b_3$ ならば \[\frac{a_1b_1+a_2b_2+a_3b_3}{3} \geqq \frac{a_1+a_2+a_3}{3}\cdot\frac{b_1+b_2+b_3}{3}\]
(参考: $2017$ 立正大)
解答例 1
$a = \dfrac{y+z}{2},$ $b = \dfrac{z+x}{2},$ $c = \dfrac{x+y}{2}$ とおく.
このとき,
\[ x = b+c-a, \quad y = c+a-b, \quad z = a+b-c\]
であるから, $2$ 変数の相加・相乗平均の不等式により
\[\begin{aligned}
&\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y} \\
&= \frac{b+c-a}{2a}+\frac{c+a-b}{2b}+\frac{a+b-c}{2c} \\
&= \frac{1}{2}\left(\frac{b}{c}+\frac{c}{b}\right) +\frac{1}{2}\left(\frac{c}{a}+\frac{a}{b}\right) +\frac{1}{2}\left(\frac{a}{b}+\frac{b}{a}\right) -\frac{3}{2} \\
&\geqq \sqrt{\frac{b}{c}\cdot\frac{c}{b}}+\sqrt{\frac{c}{a}\cdot\frac{a}{c}}+\sqrt{\frac{a}{b}\cdot\frac{b}{a}}-\frac{3}{2} \\
&= 1+1+1-\frac{3}{2} = \frac{3}{2}
\end{aligned}\]
が得られる.
解答例 2
\[\begin{aligned}
P &= \frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}, \\
Q &= \frac{y}{y+z}+\frac{z}{z+x}+\frac{x}{x+y}, \\
R &= \frac{z}{y+z}+\frac{x}{z+x}+\frac{y}{x+y} \\
\end{aligned}\]
とおく.
このとき,
\[ Q+R = \frac{y+z}{y+z}+\frac{z+x}{z+x}+\frac{x+y}{x+y} = 3\]
であり, $3$ 変数の相加・相乗平均の不等式により
\[\begin{aligned}
P\!+\!Q &= \frac{x+y}{y+z}\!+\!\frac{y+z}{z+x}\!+\!\frac{z+x}{x+y} \geqq 3\sqrt[3]{\frac{x+y}{y+z}\!\cdot\!\frac{y+z}{z+x}\!\cdot\!\frac{z+x}{x+y}} = 3, \\
P\!+\!R &= \frac{z+x}{y+z}\!+\!\frac{x+y}{z+x}\!+\!\frac{y+z}{x+y} \geqq 3\sqrt[3]{\frac{z+x}{y+z}\!\cdot\!\frac{x+y}{z+x}\!\cdot\!\frac{y+z}{x+y}} = 3
\end{aligned}\]
が成り立つから,
\[\begin{aligned}
2P+Q+R &\geqq 6 \\
2P+3 &\geqq 6 \\
P &\geqq \frac{3}{2} \\
\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y} &\geqq \frac{3}{2}
\end{aligned}\]
が得られる.
解答例 3
$x \geqq y \geqq z$ としても一般性を失わない.
このとき, $x+y \geqq z+x \geqq y+z$ から $\dfrac{1}{y+z} \geqq \dfrac{1}{z+x} \geqq \dfrac{1}{x+y}$ であるので,「並べ替え不等式」により
\[\begin{aligned}
\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y} &\geqq \frac{y}{y+z}+\frac{z}{z+x}+\frac{x}{x+y}, \\
\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y} &\geqq \frac{z}{y+z}+\frac{x}{z+x}+\frac{y}{x+y}
\end{aligned}\]
が成り立つ.
辺々を加えると
\[\begin{aligned}
2\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\right) &\geqq \frac{y+z}{y+z}+\frac{z+x}{z+x}+\frac{x+y}{x+y} = 3 \\
\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y} &\geqq \frac{3}{2}
\end{aligned}\]
が得られる.
解答例 4
$x \geqq y \geqq z$ としても一般性を失わない.
このとき, $x+y \geqq z+x \geqq y+z$ から $\dfrac{1}{y+z} \geqq \dfrac{1}{z+x} \geqq \dfrac{1}{x+y}$ であるので,「チェビシェフの和の不等式」により
\[\begin{aligned}
&\frac{1}{3}\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\right) \\
&\geqq \frac{x+y+z}{3}\cdot\frac{1}{3}\left(\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y}\right) \\
&= \frac{1}{9}\left( 3+\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\right)
\end{aligned}\]
が成り立つ.
これを整理すると, 求める不等式が得られる.
解答例 5
両辺の差をとると
\[\begin{aligned}
&\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}-\frac{3}{2} \\
&= \left(\frac{x}{y+z}-\frac{1}{2}\right) +\left(\frac{y}{z+x}-\frac{1}{2}\right) +\left(\frac{z}{x+y}-\frac{1}{2}\right) \\
&= \frac{(x-y)-(z-x)}{2(y+z)}+\frac{(y-z)-(x-y)}{2(z+x)}+\frac{(z-x)-(y-z)}{2(x+y)} \\
&= \frac{y-z}{2}\left(\frac{1}{z+x}-\frac{1}{x+y}\right) +\frac{z-x}{2}\left(\frac{1}{x+y}-\frac{1}{y+z}\right) \\
&\qquad +\frac{x-y}{2}\left(\frac{1}{y+z}-\frac{1}{z+x}\right) \\
&= \frac{(y-z)^2}{2(z+x)(x+y)}+\frac{(z-x)^2}{2(x+y)(y+z)}+\frac{(x-y)^2}{2(y+z)(z+x)} \\
&\geqq 0
\end{aligned}\]
となるから, 求める不等式が成り立つ.
参考
- 本問で示した不等式は「ネスビットの不等式」(Nesbitt's inequality) として知られている.
- これは $x_i \geqq 0,$ $x_i+x_{i+1} > 0,$ $x_n+x_1 > 0$ を満たす $12$ 個以下の偶数個, または $23$ 個以下の奇数個の変数 $x_1,$ $\cdots,$ $x_n$ に対して成り立つ「シャピロの不等式」(Shapiro inequality) \[\frac{x_1}{x_2+x_3}+\cdots +\frac{x_{n-2}}{x_{n-1}+x_n}+\frac{x_{n-1}}{x_n+x_1}+\frac{x_n}{x_1+x_2} \geqq \frac{n}{2}\] の $n = 3$ の場合である.
