平均値の定理
平均値の定理
定理《ラグランジュの平均値の定理》
実数値関数 $f(x)$ が閉区間 $[a,b]$ において連続であり, 開区間 $(a,b)$ において微分可能であるならば,
\[\frac{f(b)-f(a)}{b-a} = f'(c), \quad a < c < b\]
を満たす実数 $c$ が存在する.
問題《コーシーの平均値の定理》
$a < b$ とする.
関数 $f(x),$ $g(x)$ は閉区間 $[a,b]$ において連続であり, 開区間 $(a,b)$ において導関数 $f'(x),$ $g'(x)$ をもち, $g'(x) \neq 0$ であるとする.
- (1)
- 関数 \[ h(x) = f(x)-\frac{f(b)-f(a)}{g(b)-g(a)}\{ g(x)-g(a)\}\] とロルの定理を用いて, 開区間 $(a,b)$ において \[\frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(c)}{g'(c)}\] なる実数 $c$ が存在することを示せ.
- (2)
- 開区間 $(a,b)$ において \[\frac{f(b)-f(a)}{b-a} = f'(c)\] なる実数 $c$ が存在することを示せ.
(参考: $1973$ 和歌山県立医科大)
解答例
- (1)
- 関数 \[ h(x) = f(x)-\frac{f(b)-f(a)}{g(b)-g(a)}\{ g(x)-g(a)\}\] は $[a,b]$ において連続であり, $(a,b)$ において導関数 \[ h'(x) = f'(x)-\frac{f(b)-f(a)}{g(b)-g(a)}g'(x)\] をもつ. \[\begin{aligned} h(a) &= f(a)-\frac{f(b)-f(a)}{g(b)-g(a)}\{ g(a)-g(a)\} = f(a), \\ h(b) &= f(b)-\frac{f(b)-f(a)}{g(b)-g(a)}\{ g(b)-g(a)\} = f(a) \end{aligned}\] よって \[ h(a) = h(b)\] であるから, ロルの定理により $(a,b)$ において \[ h'(c) = f'(c)-\frac{f(b)-f(a)}{g(b)-g(a)}g'(c) = 0\] つまり \[\frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(c)}{g'(c)}\] を満たす実数 $c$ が存在する.
- (2)
- $g(x) = x$ とすると $g'(x) = 1$ となるので, (1) から求める結果が得られる.
参考
(1), (2) の結果はそれぞれ「コーシーの平均値の定理」(Cauchy's mean value theorem),「ラグランジュの平均値の定理」(Lagrange's mean value theorem) と呼ばれる.
問題《定数関数の特徴付け》
定義域全体で微分可能な関数 $f(x)$ に対して,
$f(x)$ は定数関数 $\iff$ 定義域全体で $f'(x) = 0$
が成り立つことを示せ.
解答例
$(\Longrightarrow )$ は明らかである.
$(\Longleftarrow )$ を示すため, 定義域全体で $f'(x) = 0$ が成り立つとする.
定義域に含まれる実数 $a$ をとり, $f(a) = k$ とおく.
このとき, 定義域に含まれる各実数 $x\,(\neq a)$ に対して, $a$ と $x$ の間にある, ある実数 $c$ に対して
\[ f(x)-f(a) = (x-a)f'(c) = (x-a)\cdot 0 = 0\]
となるから, $f(x) = f(a) = k$ が成り立つ.
よって, $f(x)$ は定数関数である.
参考
一般に, 微分可能な関数 $f(x),$ $g(x)$ に対して, $f'(x) = g'(x)$ が成り立つことと, ある実数 $C$ に対して
\[ g(x) = f(x)+C\]
が成り立つことは同値である.
問題《$1$ 次関数の積の極値》
$n$ を $2$ 以上の整数とし, $\alpha _1,$ $\cdots,$ $\alpha _n$ を $\alpha _1 < \cdots < \alpha _n$ なる実数とする.
$n$ 次関数 $f(x) = (x-\alpha _1)\cdots (x-\alpha _n)$ は, $n-1$ 個の開区間 $(\alpha _1,\alpha _2),$ $\cdots,$ $(\alpha _{n-1},\alpha _n)$ において, $1$ つずつ極値をとることを示せ.
(参考: 九州大)
解答例
$k$ を $1 \leqq k \leqq n-1$ なる整数とする.
平均値の定理により,
\[ f'(c_k) = \frac{f(\alpha _{k+1})-f(\alpha _k)}{\alpha _{k+1}-\alpha _k} = 0, \quad \alpha _k < c_k < \alpha _{k+1}\]
なる実数 $c_k$ が存在する.
よって, 因数定理により, $f'(x)$ は
\[ f'(x) = (x-c_1)\cdots (x-c_{n-1})\]
と表され, $x = c_k$ の前後で符号が変化するから $x = c_k$ で極値をとる.
ゆえに, $f(x)$ は, $n-1$ 個の開区間 $(\alpha _1,\alpha _2),$ $\cdots,$ $(\alpha _{n-1},\alpha _n)$ において, $1$ つずつ極値をとる.
問題《イェンセンの不等式とその応用》
$n$ を $2$ 以上の整数とする.
- (1)
- $0 < x_1 < x < x_2$ のとき, 平均値の定理を使って \[\frac{\log x-\log x_1}{x-x_1} > \frac{\log x_2-\log x}{x_2-x}\] が成り立つことを示せ. さらに, それを使って \[\log x > \log x_1+\frac{\log x_2-\log x_1}{x_2-x_1}(x-x_1)\] が成り立つことを示せ.
- (2)
- $t_1,$ $\cdots,$ $t_n > 0,$ $t_1+\cdots +t_n = 1$ とする. $x_1,$ $\cdots,$ $x_n > 0$ のとき, \[\log\left(\sum_{k = 1}^nt_kx_k\right) \geqq \sum_{k = 1}^nt_k\log x_k \quad \cdots [*]\] が成り立つことを示せ. また, 等号成立条件を求めよ.
- (3A)
- $x_1,$ $\cdots,$ $x_n > 0$ のとき,
\[\frac{x_1+\cdots +x_n}{n} \geqq \sqrt[n]{x_1\cdots x_n}\]
が成り立つことを示せ.
また, 等号成立条件を求めよ.
(参考: $2006$ 滋賀医科大)
- (3B)
- $n$ を $2$ 以上の整数とし, $p,$ $q > 1,$ $\dfrac{1}{p}+\dfrac{1}{q} = 1$ とする.
- ①
- 正の数 $a,$ $b$ に対して \[ \frac{a}{p}+\frac{b}{q} \geqq a^{\frac{1}{p}}b^{\frac{1}{q}} \quad \cdots [1]\] が成り立つことを示せ. また, 等号成立条件を求めよ.
- ②
- $x_1,$ $\cdots,$ $x_n,$ $y_1,$ $\cdots,$ $y_n$ を正の数とする. $s = \displaystyle\sum_{k = 1}^nx_k{}^p,$ $t = \displaystyle\sum_{k = 1}^ny_k{}^q$ とし, 各番号 $k$ $(1 \leqq k \leqq n)$ に対して, $a = \dfrac{x_k{}^p}{s},$ $b = \dfrac{y_k{}^q}{t}$ に $[1]$ を適用することにより, \[\left(\sum_{k = 1}^nx_k{}^p\right) ^{\frac{1}{p}}\left(\sum_{k = 1}^ny_k{}^q\right) ^{\frac{1}{q}} \geqq \sum_{k = 1}^nx_ky_k \quad \cdots [2]\] が成り立つことを示せ. また, 等号成立条件を求めよ.
解答例
- (1)
- $f(x) = \log x$ $(x > 0)$ とおく. このとき, $f'(x) = \dfrac{1}{x}$ である. 定義域を区間 $[x_1,x],$ $[x,x_2]$ に制限して $f(x)$ に平均値の定理を適用すると, ある実数 $c,$ $d$ について \[\begin{aligned} \frac{\log x-\log x_1}{x-x_1} &= \frac{1}{c}, \quad x_1 < c < x \\ \frac{\log x_2-\log x}{x_2-x} &= \frac{1}{d}, \quad x < d < x_2 \end{aligned}\] となる. また, $(0 <)\,c < d$ から $\dfrac{1}{c} > \dfrac{1}{d}$ が成り立つ. 以上から, \[\frac{\log x-\log x_1}{x-x_1} > \frac{\log x_2-\log x}{x_2-x}\] が成り立つ. よって, \[\begin{aligned} &(x_2-x_1)(\log x-\log x_1)-(x-x_1)(\log x_2-\log x_1) \\ &= (x_2-x)(\log x-\log x_1)-(x-x_1)(\log x_2-\log x) > 0 \end{aligned}\] であるから, $\dfrac{\log x-\log x_1}{x-x_1} > \dfrac{\log x_2-\log x_1}{x_2-x_1}$ つまり \[\log x > \log x_1+\frac{\log x_2-\log x_1}{x_2-x_1}(x-x_1) \quad \cdots [1]\] が得られる.
- (2)
- (i)
- $n = 2$ のとき. $x_1 \leqq x_2$ としても一般性を失わないから, その場合を考える. $x_1 = x_2$ のとき, 不等式の等号が成り立つ. $x_1 < x_2$ のとき, $[1]$ において $x = t_1x_1+t_2x_2$ とすると, \[\begin{aligned} &\log (t_1x_1+t_2x_2) \\ &> \log x_1+\frac{\log x_2-\log x_1}{x_2-x_1}(t_1x_1+t_2x_2-x_1) \\ &= \log x_1+t_2(\log x_2-\log x_1) \quad (\because t_1+t_2 = 1) \\ &= (1-t_2)\log x_1+t_2\log x_2 \\ &= t_1\log x_1+t_2\log x_2 \end{aligned}\] となり, $[*]$ が得られる.
- (ii)
- $n = m$ ($m$: $2$ 以上の整数) のとき $[*]$ が成り立ち, 等号成立が $x_1 = \cdots = x_m$ の場合に限るとする. $n = m+1$ の場合に, $s = t_1+\cdots +t_m$ とおく. \[ u_k = \frac{t_k}{s} \quad (1 \leqq k \leqq m)\] とおくと, $u_1+\cdots +u_m = 1$ となり, \[\begin{aligned} &\log\left(\sum_{k = 1}^{m+1}t_kx_k\right) = \log\left(\sum_{k = 1}^mt_kx_k+t_{m+1}x_{m+1}\right) \\ &= \log\left( s\sum_{k = 1}^mu_kx_k+t_{m+1}x_{m+1}\right) \\ &\geqq s\log\left(\sum_{k = 1}^mu_kx_k\right) +t_{m+1}\log x_{m+1} \quad (\because \text{(i)}) \\ &\geqq s\sum_{k = 1}^mu_k\log x_k+t_{m+1}\log x_{m+1} \\ &= \sum_{k = 1}^mt_k\log x_k+t_{m+1}\log x_{m+1} \\ &= \sum_{k = 1}^{m+1}t_k\log x_k \end{aligned}\] が得られる. 等号成立は “ $\displaystyle\sum_{k = 1}^mu_kx_k = x_{m+1},$ $x_1 = \cdots = x_m$ ” つまり $x_1 = \cdots = x_m = x_{m+1}$ の場合に限る.
- (3A)
- (2) において $t_1 = \cdots = t_n = \dfrac{1}{n}$ とすると \[\begin{aligned} \log\frac{x_1+\cdots +x_n}{n} &\geqq \sum_{k = 1}^n\frac{1}{n}\log x_k = \log\sqrt[n]{x_1\cdots x_n} \\ \frac{x_1+\cdots +x_n}{n} &\geqq \sqrt[n]{x_1\cdots x_n} \end{aligned}\] が得られる. 等号成立は $x_1 = \cdots = x_n$ の場合に限る.
- (3B)
- ①
- (2) の (i) により, \[\begin{aligned} \log\left(\frac{a}{p}+\frac{b}{q}\right) &\geqq \frac{\log a}{p}+\frac{\log b}{q} = \log a^{\frac{1}{p}}b^{\frac{1}{q}} \\ \frac{a}{p}+\frac{b}{q} &\geqq a^{\frac{1}{p}}b^{\frac{1}{q}} \quad \cdots [1] \end{aligned}\] が成り立ち, 等号成立は $a = b$ の場合に限る.
- ②
- $s = \displaystyle\sum_{k = 1}^nx_k{}^p,$ $t = \displaystyle\sum_{k = 1}^ny_k{}^q$ とおく. 各番号 $k$ $(1 \leqq k \leqq n)$ に対して $a = \dfrac{x_k{}^p}{s},$ $b = \dfrac{y_k{}^q}{t}$ に $[1]$ を適用し, 辺々を加えると \[\begin{aligned} \sum_{k = 1}^n\left(\frac{x_k{}^p}{ps}+\frac{y_k{}^q}{qt}\right) &\geqq \sum_{k = 1}^n\left(\frac{x_k{}^p}{s}\right) ^{\frac{1}{p}}\left(\frac{y_k{}^q}{t}\right) ^{\frac{1}{q}} \\ \frac{1}{ps}\cdot 1+\frac{1}{qt}\cdot t &\geqq \frac{1}{s^{\frac{1}{p}}t^{\frac{1}{q}}}\sum_{k = 1}^nx_ky_k \\ 1 &\geqq \frac{1}{s^{\frac{1}{p}}t^{\frac{1}{q}}}\sum_{k = 1}^nx_ky_k \\ \left(\sum_{k = 1}^nx_k{}^p\right) ^{\frac{1}{p}}\left(\sum_{k = 1}^ny_k{}^q\right) ^{\frac{1}{q}} &\geqq \sum_{k = 1}^nx_ky_k \quad \cdots [2] \end{aligned}\] が得られる. 等号成立は, 各番号 $k$ に対して $\dfrac{x_k{}^p}{s} = \dfrac{y_k{}^q}{t}$ が成り立つ場合, つまり $x_1{}^p:y_1{}^q = \cdots = x_n{}^p:y_n{}^q$ の場合に限る.
参考
- $[*]$ の形の不等式は「イェンセンの不等式」(Jensen's inequality) と呼ばれる.
本問では, $f(x) = \log x$ のグラフが上に凸であることからこの不等式を証明したが, 逆にこの形の不等式を満たす関数のグラフは上に凸であることが知られている.
一般に, 区間 $I$ で $2$ 回微分可能な実数値関数 $f(x)$ について, 次は同値である.
- (i)
- $f(x)$ のグラフがその上の $2$ 点を結ぶ線分よりも上方にある, つまり $(a,b) \subset I,$ $0 < t < 1$ ならば
\[ f((1-t)a+tb) \geqq (1-t)f(a)+tf(b)\]
が成り立つ.
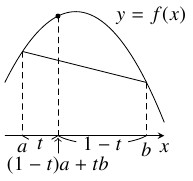
- (ii)
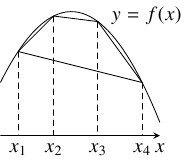
- $2$ 以上のすべての整数 $n$ に対して, $x_1,$ $\cdots,$ $x_n \in I,$ $t_1,$ $\cdots,$ $t_n \in (0,1),$ $\displaystyle\sum_{k = 1}^nt_k = 1$ ならば,「イェンセンの不等式」
\[f\left(\sum_{k = 1}^nt_kx_k\right) \geqq \sum_{k = 1}^nt_kf(x_k)\]
が成り立つ.
- (iii)
- $f(x)$ のグラフ上の点を結ぶ線分の傾きは単調減少である, つまり $(a,b) \subset I,$ $a < x < b$ ならば
\[\frac{f(x)-f(a)}{x-a} \geqq \frac{f(b)-f(x)}{b-x}\]
が成り立つ.
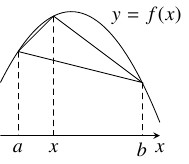
- (iv)
- $f(x)$ のグラフがその接線よりも下方にある, つまり $\alpha \in I$ ならば \[ f'(\alpha )(x-\alpha )+f(\alpha ) \geqq f(x)\] が成り立つ.
- (v)
- $f(x)$ のグラフの接線の傾きは単調減少である, つまり $f''(x) \leqq 0$ が成り立つ.
また, (i)~(v) において不等号の向きを変えた条件を満たす関数は「下に凸」(convex downward) であるという. - (2) から直ちに, $x_1,$ $\cdots,$ $x_n > 0,$ $w_1,$ $\cdots,$ $w_n \in (0,1),$ $\displaystyle\sum_{k = 1}^nw_k = 1$ のとき \[ w_1x_1+\cdots +w_nx_n \geqq x_1{}^{w_1}\cdots x_n{}^{w_n}\] の成り立つことが示される. この不等式は「重み付き相加・相乗平均の不等式」(inequality of weighted arithmetic and geometric means) として知られている.
- (3B) の ② の不等式は「ヘルダーの不等式」(Hölder's inequality) として知られており, 一般に $2$ 以上の整数 $n,$ $r$ と, $p_1,$ $\cdots,$ $p_r > 1,$ $\dfrac{1}{p_1}+\cdots +\dfrac{1}{p_r} = 1$ を満たす実数 $p_1,$ $\cdots,$ $p_r,$ 正の数 $x_{11},$ $\cdots,$ $x_{1n},$ $\cdots,$ $x_{r1},$ $\cdots,$ $x_{rn}$ に対して \[\left(\sum_{k = 1}^nx_{1k}{}^{p_1}\right) ^{\frac{1}{p_1}}\cdots\left(\sum_{k = 1}^nx_{rk}{}^{p_r}\right) ^{\frac{1}{p_r}} \geqq \sum_{k = 1}^nx_{1k}\cdots x_{rk}\] の成り立つことが知られている.
- (3B) の ② の「ヘルダーの不等式」において $p = q = 2$ とすると「コーシー=シュワルツの不等式」(こちらを参照) が得られる.
- (3B) の ② の「ヘルダーの不等式」から「ミンコフスキーの不等式」(Minkowski's inequality) \[\left(\sum_{k = 1}^n|x_k+y_k|^p\right) ^{\frac{1}{p}} \leqq \left(\sum_{k = 1}^n|x_k|^p\right) ^{\frac{1}{p}}+\left(\sum_{k = 1}^n|y_k|^p\right) ^{\frac{1}{p}}\] $(p > 1)$ を導くことができる. これは「三角不等式」(こちらを参照) の一般化であり, 物理学でも重要である.
問題《逐次代入法》
関数 $f(x) = 1+\dfrac{1}{x}$ $(x > 0)$ を用いて, 数列 $\{ a_n\}$ を
\[ a_1 = 1, \quad a_{n+1} = f(a_n)\]
で定める.
- (1)
- $f(x) = x$ はただ $1$ つの実数解 $\alpha$ をもつ. $\alpha$ の値を求めよ.
- (2)
- \[ x < \alpha \Longrightarrow f(x) > \alpha, \quad x > \alpha \Longrightarrow f(x) < \alpha\] が成り立つことを示せ.
- (3)
- $1 \leqq a_{2n-1} < \alpha < a_{2n}$ が成り立つことを示せ.
- (4)
- $\alpha -a_{2n+1} < \alpha ^{-2}(\alpha -a_{2n-1})$ が成り立つことを示せ (ヒント: $f(x)$ と区間 $[a_{2n-1},\alpha ],$ $[\alpha,a_{2n}]$ に平均値の定理の定理を適用).
- (5)
- 数列 $\{ a_{2n-1}\},$ $\{ a_{2n}\}$ はともに $\alpha$ に収束することを示せ.
(類題: $2022$ 大阪大)
解答例
- (1)
- $f(x) = x$ つまり $1+\dfrac{1}{x} = x$ の両辺に $x$ を掛けると
となるから, 求める実数解は $\alpha = \dfrac{1+\sqrt 5}{2}$ である ($x > 0$ に注意).
$x+1 = x^2$ つまり $x^2-x-1 = 0$ - (2)
- $x < \alpha$ ならば, $\dfrac{1}{x} > \dfrac{1}{\alpha}$ つまり \[ f(x) = 1+\frac{1}{x} > 1+\frac{1}{\alpha} = \alpha\] が成り立つ. 同様に, $x > \alpha$ ならば, $f(x) < \alpha$ が成り立つ.
- (3)
- (i)
- $n = 1$ のとき. $a_1 = 1 < \alpha$ であるから, $a_2 = f(a_1) > \alpha$ である.
- (ii)
- $n = k$ ($k$: 正の整数) のとき不等式が成り立つとする. このとき, $a_{2k} > \alpha$ であるから, $a_{2k+1} = f(a_{2k}) < \alpha,$ $a_{2k+2} = f(a_{2k+1}) > \alpha$ となり, $n = k+1$ のとき不等式が成り立つ.
- (4)
- $f'(x) = -\dfrac{1}{x^2}$ であるから, $f(x),$ 区間 $[a_{2n-1},\alpha ],$ $[\alpha,a_{2n}]$ に平均値の定理を適用すると,
$a_{2n-1} < c_{2n-1} < \alpha < c_{2n} < a_{2n}$ なる実数 $c_{2n-1},$ $c_{2n}$ で
\[\frac{f(a_{2n-1})-f(\alpha )}{a_{2n-1}-\alpha} = -\frac{1}{c_{2n-1}{}^2}, \quad \frac{f(a_{2n})-f(\alpha )}{a_{2n}-\alpha} = -\frac{1}{c_{2n}{}^2}\]
つまり
\[\frac{a_{2n}-\alpha}{\alpha -a_{2n-1}} = \frac{1}{c_{2n-1}{}^2}, \quad \frac{\alpha -a_{2n+1}}{a_{2n}-\alpha} = \frac{1}{c_{2n}{}^2}\]
を満たすものが存在するとわかる.
よって,
\[\frac{a_{2n}-\alpha}{\alpha -a_{2n-1}} < 1, \quad \frac{\alpha -a_{2n+1}}{a_{2n}-\alpha} < \alpha ^{-2}\]
であるから, 辺々を掛け合わせると
が得られる.
$\dfrac{\alpha -a_{2n+1}}{\alpha -a_{2n-1}} < \alpha ^{-2}$ つまり $\alpha -a_{2n+1} < \alpha ^{-2}(\alpha -a_{2n-1})$ - (5)
- (4) の結果から \[ 0 < \alpha -a_{2n-1} \leqq (\alpha ^{-2})^{n-1}(\alpha -a_1)\] が成り立ち, $0 < \alpha ^{-2} < 1$ から右辺は $0$ に収束するので, $\{ a_{2n-1}\}$ は $\alpha$ に収束する. また, (4) で示したことから \[ 0 < a_{2n}-\alpha < \alpha -a_{2n-1}\] であり, 右辺は $0$ に収束するので, $\{ a_{2n}\}$ も $\alpha$ に収束する.
参考
- 一般に, 数列 $\{ a_n\}$ が収束することと, $\{ a_{2n-1}\},$ $\{ a_{2n}\}$ が同じ値に収束することは同値である.
- 本問において, $a_n$ の値を途中まで計算することにより, $f(x) = x$ の実数解の近似値が求められる. このような方程式の解の近似値の計算方法は「逐次代入法」(method of successive substitution) と呼ばれる.
- 本問において, $a_n$ は「黄金数」(golden number) $\dfrac{1+\sqrt 5}{2}$ の「連分数展開」を途中で打ち切った「近似分数」である (こちらを参照).
