微分法の方程式への応用 (理系)
微分法の方程式への応用
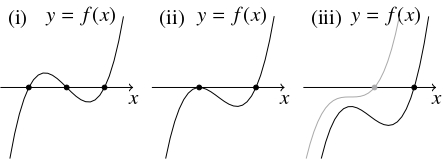
問題《$3$ 次方程式の実数解の個数》
- (1)
- $3$ 次関数 $f(x) = x^3+3px+2q$ ($p,$ $q$: 実数) の極値を求めよ.
- (2)
- (1) の $f(x)$ について, 次のことを示せ.
- (i)
- $p^3+q^2 < 0$ のとき, $f(x) = 0$ は異なる $3$ つの実数解をもつ.
- (ii)
- $p^3+q^2 = 0,$ $p < 0$ のとき, $f(x) = 0$ は異なる $2$ つの実数解をもつ.
- (iii)
- $p^3+q^2 > 0$ のとき, $f(x) = 0$ はただ $1$ つの実数解をもつ.
(参考: $2014$ 早稲田大)
解答例
- (1)
- $f(x)$ を微分すると,
\[ f'(x) = 3x^2+3p = 3(x^2+p)\]
となる.
- $p \geqq 0$ のとき. $f'(x) \geqq 0$ であるから, $f(x)$ の極値は存在しない.
- $p < 0$ のとき. \[\begin{aligned} f'(x) \geqq 0 &\iff x \leqq -\sqrt{-p},\ \sqrt{-p} \leqq x, \\ f'(x) \leqq 0 &\iff -\sqrt{-p} \leqq x \leqq \sqrt{-p} \end{aligned}\] であるから, $f(x)$ は $x = \pm\sqrt{-p}$ で極値 \[ f(\pm\sqrt{-p}) = \mp p\sqrt{-p}\pm 3p\sqrt{-p}+2q = 2(q\pm p\sqrt{-p})\] をとる.
- (2)
- $f(x) = 0$ の実数解の個数は, 曲線 $y = f(x)$ と $x$ 軸の共有点の個数に等しい.
\[ f(\sqrt{-p})f(-\sqrt{-p}) = 4(p^3+q^2)\]
であり,
\[\lim\limits_{x \to \pm\infty}f(x) = \pm\infty \quad \cdots [1]\]
であることに注意する.
- (i)
- $p^3+q^2 < 0$ のとき. $p^3 < -q^2 \leqq 0$ から $p < 0$ であるので, (1) の結果から $f(x)$ は $x = \pm\sqrt{-p}$ で極値をとる. $f(\sqrt{-p})f(-\sqrt{-p}) < 0$ であるので, $[1]$ と中間値の定理により, $y = f(x)$ と $x$ 軸は異なる $3$ 点で交わる.
- (ii)
- $p^3+q^2 = 0,$ $p < 0$ のとき. (1) の結果から $f(x)$ は $x = \pm\sqrt{-p}$ で極値をとる. $f(\sqrt{-p})f(-\sqrt{-p}) = 0,$ $f(\sqrt{-p}) \neq f(-\sqrt{-p})$ であるので, $f(\sqrt{-p}) = 0,$ $f(-\sqrt{-p}) = 0$ のいずれかが成り立つ. よって, $[1]$ と中間値の定理により, $y = f(x)$ と $x$ 軸はちょうど $2$ つの共有点をもつ.
- (iii)
- $p^3+q^2 > 0$ のとき.
- $p \geqq 0$ のとき. $f'(x) \geqq 0$ から $f(x)$ は単調増加であるので, $[1]$ と中間値の定理により, $y = f(x)$ と $x$ 軸はただ $1$ 点で交わる.
- $p < 0$ のとき. (1) の結果から $f(x)$ は $x = \pm\sqrt{-p}$ で極値をとり, $f(\sqrt{-p})f(-\sqrt{-p}) > 0$ であるので, $[1]$ と中間値の定理, $f(x)$ の増減により, $y = f(x)$ と $x$ 軸はただ $1$ 点で交わる.
参考
$3$ 次方程式 $x^3+a_2x^2+a_1x+a_0 = 0$ ($a_k$: 実数) は,
$x = X-\dfrac{a_2}{3}$ を代入して整理すると $X^3+3pX+2q = 0$ ($p,$ $q$: 実数) の形に変形でき,
その「判別式」は $-108(p^3+q^2)$ である (こちらを参照).
問題《超黄金比の評価》
$1$ 本の対角線が消えるように, 長方形 $R$ の端から最大の正方形, 最小の長方形を順に取り除いて得られる長方形が $R$ と相似になるとき, $R$ を「超黄金長方形」と呼ぶ.
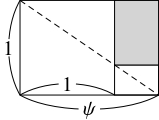 短辺の長さが $1$ である「超黄金長方形」の長辺の長さを $\psi$ とおく.
短辺の長さが $1$ である「超黄金長方形」の長辺の長さを $\psi$ とおく.

- (1)
- $\psi$ はある整数係数 $6$ 次方程式 $f(x) = 0$ の解であることを示せ. ただし, $f(x)$ の最高次の係数は $1$ とする.
- (2)
- $f(x)$ を $2$ つの整数係数 $3$ 次多項式 $g(x),$ $h(x)$ の積に分解せよ. ただし, $g(x),$ $h(x)$ の最高次の係数は $1,$ $g(x)$ の定数項は正, $h(x)$ の定数項は負とする.
- (3)
- $y = g(x),$ $y = h(x)$ のグラフに着目して, $\psi$ が $3$ 次方程式 $h(x) = 0$ の唯一の正の解であることを示せ.
- (4)
- $1.4 < \psi < 1.5$ であることを示せ.
解答例
- (1)
- この「超黄金長方形」の面積は $\psi$ である.
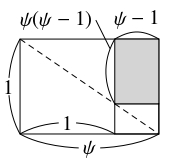
また, $1$ 本の対角線が消えるように, 端から最大の正方形, 最小の長方形を順に取り除いて得られる長方形の短辺の長さは $\psi -1,$ 長辺の長さは $\psi (\psi -1)$ である (相似比を利用した).
よって, 取り除く正方形がもとの長方形の対角線から切り取る線分の長さは \[\frac{1}{\psi}\sqrt{1+\psi ^2} = \sqrt{1+\{\psi (\psi -1)\} ^2}\] と $2$ 通りに表される. 分母を払って両辺を $2$ 乗すると \[ 1+\psi ^2 = \psi ^2\{ 1+\psi ^2(\psi -1)^2\}\] となるから, 展開して整理すると \[\psi ^6-2\psi ^5+\psi ^4 -1 = 0\] となる. よって, $\psi$ は \[ f(x) = x^6-2x^5+x^4-1\] について $f(x) = 0$ の解である.
- (2)
- $f(x)$ が整数係数 $3$ 次多項式 $g(x),$ $h(x)$ の積に分解されるとする. $f(x)$ の最高次の項は $1,$ 定数項は $-1$ であるから, \[ g(x) = x^3+ax^2+bx+1, \quad h(x) = x^3+cx^2+dx-1\] ($a,$ $b,$ $c,$ $d$: 定数) と表せる. \[\begin{aligned} g(x)h(x) &= x^6+(a+c)x^5+(ac+b+d)x^4+(ad+bc)x^3 \\ &\qquad +(bd-a+c)x^2+(-b+d)x-1 \end{aligned}\] と $f(x)$ の係数を比較すると \[\begin{aligned} &a+c = -2, \quad ac+b+d = 1, \quad ad+bc = 0, \\ &bd-a+c = 0, \quad -b+d = 0 \end{aligned}\] となるから, \[ a = -1, \quad b = 0, \quad c = -1, \quad d = 0\] が得られる. よって, $f(x)$ は \[ g(x) = x^3-x^2+1, \quad h(x) = x^3-x^2-1\] の積に分解される.
- (3)
- (1), (2) から, $\psi$ は $g(x) = 0$ または $h(x) = 0$ の正の解である. $g(x) = x^3-x^2+1$ を微分すると \[ g'(x) = 3x^2-2x = x(3x-2)\] となるから, $g(x)$ は $0 < x \leqq \dfrac{2}{3}$ で単調に減少し, $\dfrac{2}{3} \leqq x$ で単調に増加する. よって, $g(x)$ の $x > 0$ における最小値は \[ g\left(\frac{2}{3}\right) = \frac{23}{27} > 0\] であるから, $y = g(x)$ のグラフは $x$ 軸の正の部分と共有点をもたない (下図を参照). したがって, $x > 0$ において $g(x) \neq 0$ であるから, $\psi$ は $h(x) = 0$ の解である.
- 同様の議論により, $h(x)$ は $0 < x \leqq \dfrac{2}{3}$ で単調に減少し, $\dfrac{2}{3} \leqq x$ で単調に増加することがわかる. $h(0) = -1 < 0$ であるから, $y = h(x)$ のグラフは $\dfrac{2}{3} \leqq x$ において $x$ 軸と唯一の共有点をもつ (下図を参照). ゆえに, $\psi$ は $h(x) = 0$ の唯一の正の解である.
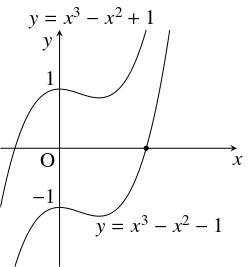
- (4)
- $h(x)$ は連続であり, \[\begin{aligned} h(1.4) &= 1.4^3-1.4^2-1 = -0.216 < 0, \\ h(1.5) &= 1.5^3-1.5^2-1 = 0.125 > 0 \end{aligned}\] を満たすから, 中間値の定理により $h(x) = 0$ は $1.4 < x < 1.5$ の範囲に解をもつ. このことと (3) の結果を合わせると, \[ 1.4 < \psi < 1.5\] が得られる.
問題《$xe^x = a$ の実数解の個数》
$a$ を実数とする.
方程式 $xe^x = a$ の実数解の個数を調べよ.
ただし, $\lim\limits_{x \to -\infty}xe^x = 0$ であること (こちらを参照) は証明なしに使ってよい.
解答例
$f(x) = xe^x$ とおく.
$xe^x = a$ の実数解の個数は, 曲線 $y = f(x)$ と直線 $y = a$ の共有点の個数に等しい.
\[ f'(x) = e^x+xe^x = (x+1)e^x\]
であるから, $f(x)$ の増減は次の表の通りである.
よって, $f(x)$ は $x = -1$ のとき極小かつ最小の値 $-\dfrac{1}{e}$ をとる.
さらに, $\lim\limits_{x \to -\infty}xe^x = 0$ から $x$ 軸は $y = f(x)$ の漸近線であるので, 曲線 $y = f(x) $ の概形は次の通りである.
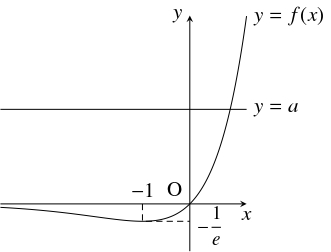 ゆえに, $xe^x = a$ の実数解の個数, つまり $y = f(x)$ と $y = a$ の共有点の個数は,
$-\dfrac{1}{e} < a < 0$ のとき $2$ 個,
$a = -\dfrac{1}{e},$ $a \geqq 0$ のとき $1$ 個,
$a < -\dfrac{1}{e}$ のとき $0$ 個である.
ゆえに, $xe^x = a$ の実数解の個数, つまり $y = f(x)$ と $y = a$ の共有点の個数は,
$-\dfrac{1}{e} < a < 0$ のとき $2$ 個,
$a = -\dfrac{1}{e},$ $a \geqq 0$ のとき $1$ 個,
$a < -\dfrac{1}{e}$ のとき $0$ 個である.
| $x$ | $\cdots$ | $-1$ | $\cdots$ |
| $f'(x)$ | $\cdots$ | $0$ | $\cdots$ |
| $f(x)$ | $\searrow$ | $-\dfrac{1}{e}$ | $\nearrow$ |

参考
- $x = ye^y$ により $x$ の値に $y$ の値を対応させる対応を「ランベルト $W$ 関数」(Lambert $W$ function) または「対数乗積関数」(product logarithm function) と呼び, $W(x)$ で表す. 本問の結果により, $x \geqq -\dfrac{1}{e}$ であり, $x = -\dfrac{1}{e},$ $x \geqq 0$ のとき $x$ の値に対応する $y$ の値はただ $1$ つであるが, $-\dfrac{1}{e} < x < 0$ のとき $x$ の値に対応する $y$ の値は $2$ つある. このように, $1$ つの $x$ の値に複数の $y$ の値が対応しているとき, $y$ を $x$ の「多価関数」(multivalued function) と呼ぶ.
- 「ランベルト $W$ 関数」は, 組合せ論, 物理学などにおいて有用であり, 指数関数を含むさまざまな方程式を解く際に利用される. 例えば, 「ランベルト $W$ 関数」を使って, $2^x = x^2$ の実数解を表すことができる (こちらを参照).
