恒等式と等式の証明
恒等式
定理《ラグランジュの恒等式》
正の整数 $n$ に対して
\[\left(\sum_{k = 1}^nx_k{}^2\right)\!\!\!\left(\sum_{k = 1}^ny_k{}^2\right)\!\!-\!\!\left(\sum_{k = 1}^nx_ky_k\right) ^2 \!\!=\!\! \sum_{1 \leqq k < l \leqq n}\!\!\!(x_ky_l\!\!-\!\!x_ly_k)^2\]
が成り立つ.
ここで, 右辺の和は $1 \leqq k < l \leqq n$ を満たす整数の組 $(k,l)$ すべてにわたる和を表す.
問題《ラグランジュの恒等式とその応用》
- (1)
- $(ac\!+\!bd)^2\!+\!(ad\!-\!bc)^2 \!=\! (a^2\!+\!b^2)(c^2\!+\!d^2)$ を示せ.
- (2)
- 頂点の各座標が整数である正三角形は存在しないことを示せ. ただし, $\sqrt 3$ が無理数であることは, 証明なしに用いてよい.
解答例
- (1)
- 左辺を展開して整理すると, \[\begin{aligned} &(ac+bd)^2+(ad-bc)^2 \\ &= (a^2c^2+2abcd+b^2d^2)+(a^2d^2-2abcd+b^2c^2) \\ &= a^2c^2+a^2d^2+b^2c^2+b^2d^2 \\ &= a^2(c^2+d^2)+b^2(c^2+d^2) \\ &= (a^2+b^2)(c^2+d^2) \quad \cdots [1] \end{aligned}\] となる.
- (2)
- 頂点の各座標が整数である正三角形の存在を仮定する.
必要に応じて各頂点を平行移動すると,
ある整数 $a,$ $b,$ $c,$ $d$ について $\mathrm O(0,\ 0),$ $\mathrm P(a,\ b),$ $\mathrm Q(c,\ d)$ を頂点とする正三角形が得られる.
$\mathrm{OP} = \mathrm{OQ}$ すなわち $\mathrm{OP}^2 = \mathrm{OQ}^2$ から,
\[ a^2+b^2 = c^2+d^2 \quad \cdots [2]\]
が成り立つ.
また, $\mathrm{OQ} = \mathrm{PQ}$ すなわち $\mathrm{OQ}^2 = \mathrm{PQ}^2$ から,
\[ c^2+d^2 = (a-c)^2+(b-d)^2\]
が成り立つ.
右辺を展開し, $ac+bd$ について解くと,
\[ ac+bd = \frac{1}{2}(a^2+b^2) \quad \cdots [3]\]
が得られる.
$[2],$ $[3]$ を $[1]$ に代入, 整理して分母を払うと,
\[\begin{aligned}
3(a^2+b^2)^2 &= 4(ad-bc)^2 \\
\sqrt 3(a^2+b^2) &= 2|ad-bc| \\
\sqrt 3 &= \dfrac{2|ad-bc|}{a^2+b^2}
\end{aligned}\]
となる.
この分母, 分子は整数だから,「$\sqrt 3$ が有理数」という矛盾が生じる.
ゆえに, 頂点の各座標が整数である正三角形は存在しない.
背景
- (1) の等式は「ラグランジュの恒等式」(Lagrange's equality)として知られている.
- 座標平面上の各座標が整数である点を「格子点」(lattice point)と呼び, すべての頂点が格子点であるような多角形を「格子多角形」(lattice polygon)と呼ぶ.
- 「格子正多角形」は正方形に限ることが知られている.
(2) の別解については, こちらを参照されたい.
定理《ブラーマグプタの恒等式》
\[\begin{aligned}
(x^2+ny^2)(u^2+nv^2) &= (xu+nyv)^2+n(xv-yu)^2 \\
&= (xu-nyv)^2+n(xv+yu)^2
\end{aligned}\]
が成り立つ.
問題《ブラーマグプタの恒等式とペル方程式》
- (1)
- $(xu+dyv)^2-d(xv+yu)^2 = (x^2-dy^2)(u^2-dv^2)$ が成り立つことを示せ.
- (2)
- $u^2-2v^2 = 1$ の正の整数解を $1$ つ求めよ.
- (3)
- $x^2-2y^2 = -1$ は無限に多くの整数解をもつことを示せ.
解答例
- (1)
- 左辺を展開して整理すると, \[\begin{aligned} &(xu+dyv)^2-d(xv+yu)^2 \\ &= (x^2u^2+2dxyuv+d^2y^2v^2) \\ &\qquad -(dx^2v^2+2dxyuv+dy^2u^2) \\ &= x^2u^2-dx^2v^2-dy^2u^2+d^2y^2v^2 \\ &= (x^2-dy^2)(u^2-dv^2) \quad \cdots [1] \end{aligned}\] となる.
- (2)
- $(u,v) = (3,2)$ は \[ u^2-2v^2 = 1 \quad \cdots [2]\] を満たす.
- (3)
- $(x,y) = (1,1)$ は $x^2-2y^2 = -1$ を満たす. また, $[1]$ に $d = 2,$ $(u,v) = (3,2)$ を代入すると, $[2]$ から, \[ x^2-2y^2 = (3x+4y)^2-2(2x+3y)^2\] となる. そこで, $x_n,$ $y_n$ $(n \geqq 1)$を \[\begin{aligned} x_1 &= 1, & x_{n+1} &= 3x_n+4y_n, \\ y_1 &= 1, & y_{n+1} &= 2x_n+3y_n \end{aligned}\] で定めると, $(x,y) = (x_n,y_n)$ は $x^2-2y^2 = -1$ の整数解になる. $x_{n+1} > x_n$ に注意すると, これらの解は互いに異なる. ゆえに, $x^2-2y^2 = -1$ は無限に多くの整数解をもつ.
背景
- (1) の等式は「ブラーマグプタの恒等式」と呼ばれる.
- 平方数でない正の整数 $d$ に対して,「ペル方程式」$x^2-dy^2 = 1$ は無限に多くの整数解をもつことが知られているが, $x^2-dy^2 = -1$ は無限に多くの整数解をもつこともあれば, 全く整数解をもたないことがある(こちらを参照).
比例式
問題《合比・除比・合除比の理》
- (1)
- (i)
- $\dfrac{a}{b} = \dfrac{c}{d}$ $\Longrightarrow$ $\dfrac{a+b}{b} = \dfrac{c+d}{d}$
- (ii)
- $\dfrac{a}{b} = \dfrac{c}{d}$ $\Longrightarrow$ $\dfrac{a-b}{b} = \dfrac{c-d}{d}$
- (iii)
- $\dfrac{a}{b} = \dfrac{c}{d}$ $\Longrightarrow$ $\dfrac{a+b}{a-b} = \dfrac{c+d}{c-d}$
- (2)
- (1) の結果を利用して, (i)～(iii) の逆が成り立つことを示せ.
解答例
- (1)
- $\dfrac{a}{b} = \dfrac{c}{d}$ を仮定する.
(i), (ii): 両辺に $\pm 1$ を加えると, \[\frac{a}{b}+1 = \frac{c}{d}+1, \quad \frac{a}{b}-1 = \frac{c}{d}-1\] から \[\frac{a+b}{b} = \frac{c+d}{d}, \quad \frac{a-b}{b} = \frac{c-d}{d}\] が得られる.
(iii): $2$ 式の辺々を割ると, \[\frac{a+b}{b}\cdot\frac{b}{a-b} = \frac{c+d}{d}\cdot\frac{d}{c-d}\] から \[\frac{a+b}{a-b} = \frac{c+d}{c-d}\] が得られる. - (2)
- (i) の逆: $\dfrac{a+b}{b} = \dfrac{c+d}{d}$ に (ii) を適用すると,
$\dfrac{(a+b)-b}{b} = \dfrac{(c+d)-d}{d}$ つまり $\dfrac{a}{b} = \dfrac{c}{d}$が得られる.
(ii) の逆: $\dfrac{a-b}{b} = \dfrac{c-d}{d}$ に (i) を適用すると,$\dfrac{(a-b)+b}{b} = \dfrac{(c-d)+d}{d}$ つまり $\dfrac{a}{b} = \dfrac{c}{d}$が得られる.
(iii) の逆: $\dfrac{a+b}{a-b} = \dfrac{c+d}{c-d}$ に (iii) を適用すると,$\dfrac{(a+b)+(a-b)}{(a+b)-(a-b)} = \dfrac{(c+d)+(c-d)}{(c+d)-(c-d)},$が得られる.
$\dfrac{2a}{2b} = \dfrac{2c}{2d}$ つまり $\dfrac{a}{b} = \dfrac{c}{d}$
背景
(i), (ii), (iii) はそれぞれ,「合比の理」,「除比の理」,「合除比の理」として知られている.
問題《加比の理》
実数 $a,$ $b,$ $c,$ $d,$ $x,$ $y$ が $bd \neq 0,$ $\dfrac{a}{b} = \dfrac{c}{d},$ $bx+dy \neq 0$ を満たすとき, $\dfrac{ax+cy}{bx+dy}$ の値を求めよ.
解答例
$k = \dfrac{a}{b} = \dfrac{c}{d}$ とおくと,
\[ a = bk, \quad c = dk\]
となるから,
\[\begin{aligned}
\frac{ax+cy}{bx+dy} &= \frac{bkx+dky}{bx+dy} = \frac{k(bx+dy)}{bx+dy} \\
&= k = \frac{a}{b} = \frac{c}{d}
\end{aligned}\]
である.
背景
- 本問の結果を「加比の理」と呼ぶ.
- 「加比の理」は, 平面上のベクトル $\vec v = (a,b)$ と $\vec w = (c,d)$ が互いに平行なとき, $x\vec v+y\vec w = (ax+cy,bx+dy)$ もそれに平行であることを示している.
問題《シュケの不等式》
正の数 $a,$ $b,$ $c,$ $d$ に対して, $\dfrac{a}{b} < \dfrac{c}{d}$ であるとき,
\[\frac{a}{b} < \frac{a+c}{b+d} < \frac{c}{d}\]
が成り立つことを示せ.
(参考: 2008 お茶の水女子大)
解答例
$\dfrac{a}{b} < \dfrac{c}{d}$ のとき,
$ad < bc$ つまり $ad-bc < 0$
であるから,
\[\begin{aligned}
\frac{a}{b}-\frac{a+c}{b+d} &= \frac{a(b+d)-(a+c)b}{b(b+d)} = \frac{ad-bc}{b(b+d)} < 0, \\
\frac{a+c}{b+d}-\frac{c}{d} &= \frac{(a+c)d-c(b+d)}{(b+d)d} = \frac{ad-bc}{(b+d)d} < 0
\end{aligned}\]
が成り立つ.
よって, 求める不等式が成り立つ.
背景
- 中世フランスの数学者シュケ (N. Chuquet)は, 本問の不等式を利用して $\sqrt 6$ の近似値を計算した.
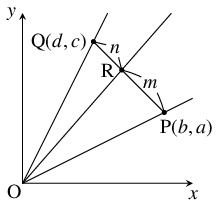
- より一般に, 正の数 $a,$ $b,$ $c,$ $d,$ $m,$ $n$ に対して
\[\frac{a}{b} < \frac{c}{d} \Longrightarrow \frac{a}{b} < \frac{na+mc}{nb+md} < \frac{c}{d}\]
が成り立つが, それは平面上の点 $\mathrm P(b,a)$ と原点を結ぶ直線,
点 $\mathrm Q(d,c)$ と原点を結ぶ直線の間に,
線分 $\mathrm{PQ}$ を $m:n$ に内分する点 $\mathrm R\left(\dfrac{nb+md}{m+n},\dfrac{na+mc}{m+n}\right)$ と原点を結ぶ直線があることからも分かる.
