いろいろな不定方程式
$2$ 次不定方程式
問題《ピタゴラスの $3$ つ組の公式の代数的証明》
互いに素な正の整数 $a,$ $b,$ $c$ が $a^2+b^2 = c^2$ を満たすとする.
次のことを示せ.
- (1)
- $a,$ $b$ の偶奇は異なり, $c$ は奇数である.
- (2)
- $\dfrac{c+a}{2},$ $\dfrac{c-a}{2}$ は互いに素な平方数である.
- (3)
- $a,$ $b,$ $c$ は, 互いに素で偶奇の異なる正の整数 $m,$ $n$ $(m > n)$ を用いて \[ a = m^2-n^2, \quad b = 2mn, \quad c = m^2+n^2 \quad \cdots [*]\] と表される.
解答例
- (1)
- $a,$ $b$ の偶奇が一致するとして, 矛盾を導く.
- (i)
- $a,$ $b$ が偶数であるとき. $a^2+b^2 = c^2$ は偶数になり, よって $c$ は偶数になるが, これは $a,$ $b,$ $c$ が互いに素であることに反する.
- (ii)
- $a,$ $b$ が奇数であるとき.
すべての整数は $2d$ または $2d+1$
($d$: 整数) の形に表され, \[\begin{aligned} (2d)^2 &= 4d^2, \\ (2d+1)^2 &= 4(d^2+d)+1 \end{aligned}\] を $4$ で割った余りはそれぞれ $0,$ $1$ である. よって, $a^2+b^2 = c^2$ を $4$ で割った余りは $1+1 = 2$ となるが, これは $c^2$ を $4$ で割った余りが $0$ または $1$ であることに反する.
- (2)
- $a^2+b^2 = c^2$ を変形すると,
\[\begin{aligned}
b^2 &= c^2-a^2 = (c+a)(c-a) \\
\left(\frac{b}{2}\right) ^2 &= \frac{c+a}{2}\cdot\dfrac{c-a}{2} \quad \cdots [1]
\end{aligned}\]
となる.
仮定から, $\dfrac{b}{2},$ $\dfrac{c+a}{2},$ $\dfrac{c-a}{2}$ は整数である.
仮に $\dfrac{c+a}{2},$ $\dfrac{c-a}{2}$ が共通の素因数 $p$ をもつとすると, これらの整数は正の整数 $x,$ $y$ を用いて \[\frac{c+a}{2} = px, \quad \frac{c-a}{2} = py\] と表され, \[ c = p(x+y), \quad a = p(x-y), \quad b = p^2(x+y)(x-y)\] は $p$ の倍数になるが, これは $a,$ $b,$ $c$ が互いに素であることに反する.
ゆえに, $\dfrac{c+a}{2},$ $\dfrac{c-a}{2}$ は, 互いに素であり, $[1]$ と素因数分解の一意性により平方数である. - (3)
- (2) から, $\dfrac{c+a}{2},$ $\dfrac{c-a}{2}$ は互いに素な整数 $m,$ $n$ $(m > n)$ を用いて \[\frac{c+a}{2} = m^2 \quad \cdots [2], \quad \frac{c-a}{2} = n^2 \quad \cdots [3]\] と表される. $a = m^2-n^2$ は奇数であるから, $m^2,$ $n^2$ の偶奇は異なり, よって $m,$ $n$ の偶奇は異なる. $[2]-[3],$ $[2]+[3]$ から \[ a = m^2-n^2, \quad c = m^2+n^2\] が得られる. さらに, \[\begin{aligned} b^2 &= c^2-a^2 = (m^2+n^2)^2-(m^2-n^2)^2 \\ &= (m^4+2m^2n^2+n^4)-(m^4-2m^2n^2+n^4) \\ &= 4m^2n^2 \end{aligned}\] から \[ b = 2mn\] である. これで, 求める公式 $[*]$ が得られた.
参考
- 三平方の定理に現れる方程式 $a^2+b^2 = c^2$ を「ピタゴラスの方程式」と呼び, その正の整数解 $(a,b,c)$ を「ピタゴラスの $3$ つ組」(Pythagorean triple) または「ピタゴラス数」と呼ぶ (こちらを参照).
- 「ピタゴラスの $3$ つ組」は, $3$ 辺の長さがすべて整数である直角三角形の辺の長さの組に他ならない. このような直角三角形は「ピタゴラスの三角形」(Pythagorean triangle) と呼ばれ, 古くから直角の計測に利用されていたと考えられている.
- 公式 $[*]$ から,「ピタゴラスの三角形」のさまざまな性質が導かれる. 例えば, すべての「ピタゴラスの三角形」の内接円の半径は整数であることがわかる. 実際, $3$ 辺の長さが $a = k(m^2-n^2),$ $b = 2kmn,$ $c = k(m^2+n^2)$ ($k,$ $m,$ $n$: 正の整数, $m > n$) である直角三角形の内接円の半径を $r$ とおくと, \[\frac{ar}{2}+\dfrac{br}{2}+\frac{cr}{2} = \dfrac{ab}{2}\] となるから, \[\begin{aligned} r &= \frac{ab}{a+b+c} = \frac{k(m^2-n^2)\cdot 2kmn}{k(m^2-n^2)+2kmn+k(m^2+n^2)} \\ &= \frac{2k^2mn(m+n)(m-n)}{2km(m+n)} = kn(m-n) \end{aligned}\] は整数になる. 直角を挟む $2$ 辺の長さの少なくとも一方が $3$ の倍数であること, $3$ 辺の長さの少なくとも $1$ つが $5$ の倍数であることも容易に証明できる (こちらを参照).
- 本問で示した公式の別証明については, こちらとこちらを参照されたい.
問題《ピタゴラスの $3$ つ組の性質: 方程式》
$3$ 辺の長さが整数である直角三角形について, 次のことを示せ.
- (A)
- 面積は $6$ の倍数である.
(参考: $2022$ 慶應義塾大, $2006$ 一橋大, $2004$ 旭川医科大ほか)
- (B)
- 少なくとも $1$ つの辺の長さは $5$ の倍数である.
(参考: $2021$ 東京海洋大, $2004$ 防衛医科大)
解答例
直角三角形の $3$ 辺の長さ $a,$ $b,$ $c$ $(a < c,$ $b < c)$ が整数であるとする.
- (A)
- 面積 $\dfrac{ab}{2}$ が $6$ の倍数であることを示すには, $ab$ が $12 = 3\cdot 4$ の倍数であることを示せばよいから,
- (I)
- $a$ または $b$ が $3$ の倍数であること
- (II)
- $a$ または $b$ が $4$ の倍数であること
- (I)
- $a,$ $b$ が $3$ の倍数でないとして, $a^2+b^2$ が平方数でないことを示す.
すべての整数は $3d,$ $3d\pm 1$ ($d$: 整数) のいずれかの形に表され,
- $(3d)^2 = 3\cdot 3d^2$ を $3$ で割った余りは $0$ ($3d^2$ は整数),
- $(3d\pm 1)^2 = 3(3d^2\pm 2d)+1$ を $3$ で割った余りは $1$ ($3d^2\pm 2d$ は整数)
- (II)
- $a,$ $b$ が $4$ の倍数でないとして, $a^2+b^2$ が平方数でないことを示す.
すべての整数は $2d+1$ (奇数), $4d+2$ ($4$ の倍数でない偶数), $4d$ ($4$ の倍数) ($d$: 整数) のいずれかの形に表され,
- $(2d+1)^2 = 4d(d+1)+1$ を $4,$ $8$ で割った余りは $1$ ($d(d+1)$ は偶数),
- $(4d+2)^2 = 16d(d+1)+4$ を $8,$ $16$ で割った余りは $4$ ($d(d+1)$ は整数),
- $(4d)^2 = 8\cdot 2d^2$ を $8$ で割った余りは $0$ ($2d^2$ は整数)
- (i)
- $a,$ $b$ が奇数のとき. $a^2+b^2$ を $4$ で割った余りは $1+1 = 2$ であり, $a^2+b^2$ の素因数分解における $2$ の指数は $1$ であるから, $a^2+b^2$ は平方数でない.
- (ii)
- $a,$ $b$ の一方が奇数, 他方が $4$ の倍数でない偶数のとき. $a^2+b^2$ を $8$ で割った余りは $1+4 = 5$ であるが, 平方数を $8$ で割った余りは $0,$ $1$ または $4$ であるから, $a^2+b^2$ は平方数でない.
- (iii)
- $a,$ $b$ が $4$ の倍数でない偶数のとき. $a^2+b^2$ を $16$ で割った余りは $4+4 = 8$ であり, $a^2+b^2$ の素因数分解における $2$ の指数は $3$ であるから, $a^2\!+\!b^2$ は平方数でない.
- (B)
- $a,$ $b$ が $5$ の倍数でないとして, $a^2+b^2$ が平方数ならば $a^2+b^2$ は $5$ の倍数であることを示せばよい.
すべての整数は $5d,$ $5d\pm 1,$ $5d\pm 2$ ($d$: 整数) のいずれかの形に表され,
- $(5d)^2 = 5\cdot 5d^2$ を $5$ で割った余りは $0$ ($5d^2$: 整数),
- $(5d\pm 1)^2 = 5(5d^2\pm 2d)+1$ を $5$ で割った余りは $1$ ($5d^2\pm 2d$: 整数),
- $(5d\pm 2)^2 = 5(5d^2\pm 4d)+4$ を $5$ で割った余りは $4$ ($5d^2\pm 4d$: 整数)
一方, 平方数を $5$ で割った余りは $0,$ $1$ または $4$ であるから, $a^2+b^2$ が平方数ならば $a^2+b^2$ は $5$ の倍数である. ゆえに, $3$ 辺の長さが整数である直角三角形において, 少なくとも $1$ つの辺の長さは $5$ の倍数である.
参考
問題《ピタゴラスの $4$ つ組の性質: 方程式》
正の整数 $a,$ $b,$ $c,$ $d$ が $a^2+b^2+c^2 = d^2$ を満たすとき, 次のことを示せ.
- (A)
- $a,$ $b,$ $c$ のうち少なくとも $2$ つは偶数である.
- (B)
- $a,$ $b,$ $c,$ $d$ のうち少なくとも $1$ つは $3$ の倍数である.
(参考: $1994$ 一橋大)
解答例
- (A)
- 正の整数 $a,$ $b,$ $c$ のうち少なくとも $2$ つが奇数であるとき, $a^2+b^2+c^2$ が平方数でないことを示せばよい.
整数 $k$ に対して
\[ (2k)^2 = 4k^2, \quad (2k-1)^2 = 4k(k-1)+1\]
が成り立つから, 平方数を $4$ で割った余りは $0$ か $1$ であることに注意する.
- (i)
- $a,$ $b,$ $c$ が奇数であるとき. $a^2,$ $b^2,$ $c^2$ を $4$ で割った余りは $1$ であるから, $a^2+b^2+c^2$ を $4$ で割った余りは $3$ である. よって, $a^2+b^2+c^2$ は平方数でない.
- (ii)
- $a,$ $b,$ $c$ のうち $1$ つが偶数, $2$ つが奇数であるとき. $a^2,$ $b^2,$ $c^2$ を $4$ で割った余りは $0,$ $1,$ $1$ (順不同) であるから, $a^2+b^2+c^2$ を $4$ で割った余りは $2$ である. よって, $a^2+b^2+c^2$ は平方数でない.
- (B)
- 正の整数 $a,$ $b,$ $c,$ $d$ が $a^2+b^2+c^2 = d^2$ を満たすとする. 整数 $k$ に対して \[ (3k\pm 1)^2 = 3(3k^2\pm 2k)+1\] が成り立つから, $3$ の倍数でない整数の平方を $3$ で割った余りは $1$ である. よって, $a,$ $b,$ $c$ が $3$ の倍数でないとき, $a^2+b^2+c^2$ を $3$ で割った余りは $0$ であるから, $d^2$ は $3$ の倍数であり, $d$ は $3$ の倍数である. これは, $a,$ $b,$ $c,$ $d$ のうち少なくとも $1$ つは $3$ の倍数であることを示している.
参考
- $(1,2,2,3)$ のように, $a^2+b^2+c^2 = d^2$ を満たす正の整数の組 $(a,b,c,d)$ を「ピタゴラスの $4$ つ組」(Pythagorean quadruple) と呼ぶ. この $a,$ $b,$ $c,$ $d$ は, 互いに素であるとき, 必要に応じて並べ替えれば, 非負整数 $k,$ $l,$ $m,$ $n$ を用いて \[\begin{aligned} a &= k^2+l^2-m^2-n^2, \\ b &= 2(km-ln), \\ c &= 2(kn+lm), \\ d &= k^2+l^2+m^2+n^2 \end{aligned}\] と表されることが知られている (証明は高校の範囲を超えるが, 興味があればこちらを参照).
- すべての「ピタゴラスの $4$ つ組」$(a,b,c,d)$ に対して $abcd$ を割り切る最大の整数は $12$ であることが知られている.
問題《$x^2-y^2 = a$ の整数解》
$a$ を $1$ より大きい整数とする.
各正の整数 $n$ に対して, その正の約数の個数を $d(n)$ で表す.
- (1)
- $a$ が $4$ の倍数のとき, $a = a'a''$ なる正の偶数 $a',$ $a''$ の組の個数は $d\left(\dfrac{a}{4}\right)$ であることを示せ.
- (2)
- $x^2-y^2 = a$ の正の整数解は, $a$ の正の約数 $a',$ $a''$ ($a = a'a'',$ $a' > a''$ であり, $a,$ $a',$ $a''$ の偶奇は一致) を用いて \[ x = \frac{a'+a''}{2}, \quad y = \frac{a'-a''}{2}\] と表されることを示せ.
- (3)
- $x^2-y^2 = a$ の正の整数解の個数 $N$ を, $d(a),$ $d\left(\dfrac{a}{4}\right)$ を用いて表せ.
(参考: $1983$ 大阪市立大)
解答例
- (1)
- $a$ を $4$ の倍数とする. 正の偶数 $a',$ $a''$ が $a = a'a''$ を満たすとき, $\dfrac{a'}{2},$ $\dfrac{a''}{2}$ は, \[\frac{a}{4} = \frac{a'}{2}\cdot\frac{a''}{2}\] を満たすから, $\dfrac{a}{4}$ の正の約数である. 逆に, $\dfrac{a}{4}$ の正の約数を $2$ 倍すると, $a = a'a''$ なる正の偶数 $a',$ $a''$ が得られる. よって, 条件を満たす正の偶数の組の個数は $d\left(\dfrac{a}{4}\right)$ である.
- (2)
- 正の整数 $x,$ $y$ が
を満たすとして, \[ x+y = a', \quad x-y = a''\] とおく. このとき, $a',$ $a''$ は $a = a'a'',$ $a' > a''$ なる $a$ の正の約数である. 整数 $x,$ $y$ の $2$ 倍 \[ 2x = a'+a'' \quad \cdots [1], \quad 2y = a'-a'' \quad \cdots [2]\] は偶数であるから, $a',$ $a''$ の偶奇は一致する. よって, $a$ が奇数のとき $a',$ $a''$ は奇数, $a$ が $4$ の倍数のとき $a',$ $a''$ は偶数であり, $[1],$ $[2]$ の両辺を $2$ で割ると \[ x = \frac{a'+a''}{2}, \quad y = \frac{a'-a''}{2}\] が得られる. $a$ を $4$ で割った余りが $2$ のとき, $a = a'a''$ を満たす整数 $a',$ $a''$ の偶奇は異なるから, $[1],$ $[2]$ は成り立たず, よって $x^2-y^2 = a$ は整数解をもたない.
$x^2-y^2 = a$ つまり $(x+y)(x-y) = a$ - (3)
- (2) の議論から, $x^2-y^2 = a$ の正の整数解の個数は, $a = a'a'',$ $a' > a''$ を満たし, $a$ と偶奇が等しい正の整数 $a',$ $a''$ の組の個数に等しい. その個数は, $a$ が平方数でないとき $a$ または $\dfrac{a}{4}$ の正の約数の個数の半分であり, $a$ が平方数のとき $a$ または $\dfrac{a}{4}$ の正の約数の個数から $\sqrt a$ または $\dfrac{\sqrt a}{2}$ の $1$ 個を引いた個数の半分であるから, \[ N = \begin{cases} \dfrac{1}{2}d(a) & (a\text{ が奇数で, 平方数でない}) \\[2mm] \dfrac{1}{2}\{ d(a)-1\} & (a\text{ が奇数で, 平方数}) \\[2mm] 0 & (a\text{ を }4\text{ で割った余りが }2) \\ \dfrac{1}{2}d\left(\dfrac{a}{4}\right) & (a\text{ が }4\text{ の倍数で, 平方数でない}) \\[2mm] \dfrac{1}{2}\left\{ d\left(\dfrac{a}{4}\right) -1\right\} & (a\text{ が }4\text{ の倍数で, 平方数}) \end{cases}\] である.
参考
\[ x^2+y^2 = z^2 \iff z^2-y^2 = x^2 \iff z^2-x^2 = y^2\]
であるから, 本問の結果を使うと, 与えられた整数 $k$ に対して「ピタゴラスの方程式」$x^2+y^2 = z^2$ が $x = k$ または $y = k$ のときにいくつ解をもつかを調べられる.
$k$ の素因数分解が $k = 2^{e_0}p_1{}^{e_1}\cdots p_r{}^{e_r}$ $(e_0,e_1,\cdots,e_r \geqq 0)$ であるとき, $a = k$ または $b = k$ であるような「ピタゴラスの $3$ つ組」 $(a,b,c)$ の個数は
\[\begin{cases}
\dfrac{(2e_0-1)(2e_1+1)\cdots (2e_r+1)-1}{2} & (e_0 > 0), \\
\dfrac{(2e_1+1)\cdots (2e_r+1)-1}{2} & (e_0 = 0)
\end{cases}\]
である.
問題《ペル方程式の一般解》
$\alpha = a_1+a_1\sqrt 2$ ($a_1,$ $a_2$: 整数) の形に表される各実数 $\alpha$ に対して, $\alpha ' = a_1-a_2\sqrt 2$ と定める.
- (1)
- $\alpha = a_1+a_2\sqrt 2,$ $\beta = b_1+b_2\sqrt 2$ ($a_1,$ $a_2,$ $b_1,$ $b_2$: 整数) とする. このとき, $(\alpha\beta )' = \alpha '\beta '$ が成り立つことを示せ.
- (2)
- $x^2-2y^2 = 1$ の正の整数解 $(x,y)$ を用いて $x+y\sqrt 2$ の形に表される実数の最小値を $\varepsilon$ とおく. $\varepsilon$ の値を求めよ.
- (3)
- (2) の $\varepsilon,$ 正の整数 $n$ に対して, \[\varepsilon ^n = x_n+y_n\sqrt 2 \quad \cdots [\mathrm A]\] により整数 $x_n,$ $y_n$ を定める. $(x,y) = (x_n,y_n)$ は $x^2-2y^2 = 1$ の解であることを示せ. さらに, $\varepsilon,$ $\varepsilon'$ と $n$ を用いて $x_n,$ $y_n$ を表せ.
- (4)
- $(x,y)$ を $x^2-2y^2 = 1$ の正の整数解とする. このとき, $(x,y)$ はある正の整数 $n$ に対して (3) の解 $(x_n,y_n)$ と一致することを示せ. $\sqrt 2$ が無理数であることは証明なしに使ってよい.
(参考: $1985$ 東京工業大)
解答例
- (1)
- \[\begin{aligned} \alpha\beta &= (a_1+a_2\sqrt 2)(b_1+b_2\sqrt 2) \\ &= (a_1b_1+2a_2b_2)+(a_1b_2+a_2b_1)\sqrt 2 \end{aligned}\] から, \[\begin{aligned} \alpha '\beta ' &= (a_1-a_2\sqrt 2)(b_1-b_2\sqrt 2) \\ &= (a_1b_1+2a_2b_2)-(a_1b_2+a_2b_1)\sqrt 2 = (\alpha\beta )' \end{aligned}\] が成り立つ.
- (2)
- $x+y\sqrt 2$ は $x,$ $y$ に関してそれぞれ単調増加であり, \[\begin{aligned} 1^2-2\cdot 1^2 &\neq 1, \quad 1^2-2\cdot 2^2 \neq 1, \\ 2^2-2\cdot 1^2 &\neq 1, \quad 2^2-2\cdot 2^2 \neq 1, \\ 3^2-2\cdot 1^2 &\neq 1, \quad 3^2-2\cdot 2^2 = 1 \end{aligned}\] であるから, $\varepsilon = 3+2\sqrt 2$ である.
- (3)
- $[\mathrm A]$ から, \[ x_n-y_n\sqrt 2 = (\varepsilon ^n)' \quad \cdots [\mathrm B]\] が成り立つ. よって, $[\mathrm A],$ $[\mathrm B]$ の辺々を掛け合わせると, (1) の結果により, \[\begin{aligned} x_n{}^2-2y_n{}^2 &= (x_n+y_n\sqrt 2)(x_n-y_n\sqrt 2) \\ &= \varepsilon ^n(\varepsilon ^n)' = \varepsilon ^n(\varepsilon ') ^n = (\varepsilon\varepsilon ')^n \\ &= \{ (3+2\sqrt 2)(3-2\sqrt 2)\} ^n = 1^n = 1 \end{aligned}\] となる. さらに, $[\mathrm A],$ $[\mathrm B]$ から, \[ x_n = \frac{\varepsilon ^n+\varepsilon '^n}{2}, \quad y_n = \frac{\varepsilon ^n-\varepsilon '^n}{2\sqrt 2}\] が得られる.
- (4)
- $x+y\sqrt 2 \geqq \varepsilon > 1$ であるから, \[\varepsilon ^n \leqq x+y\sqrt 2 < \varepsilon ^{n+1}\] を満たす正の整数 $n$ が存在する. 両辺を $\varepsilon ^n$ で割ると, \[ 1 \leqq (x+y\sqrt 2)\varepsilon ^{-n} < \varepsilon\] となる. $\varepsilon\varepsilon ' = 1$ から $\varepsilon ^{-n} = (\varepsilon ^{-1})^n = \varepsilon '^n = (\varepsilon ^n)' = x_n-y_n\sqrt 2$ であるので, \[\begin{aligned} (x+y\sqrt 2)\varepsilon ^{-n} &= (x+y\sqrt 2)(x_n-y_n\sqrt 2) \\ &= (xx_n-yy_n)+(-xy_n+yx_n)\sqrt 2 \end{aligned}\] が成り立つ. そこで, $a = xx_n-yy_n,$ $b = -xy_n+yx_n$ とおく. このとき, \[\begin{aligned} a+b\sqrt 2 &= (x+y\sqrt 2)\varepsilon ^{-n}, \\ a-b\sqrt 2 &= (x-y\sqrt 2)\varepsilon ^n \end{aligned}\] となるから, 辺々を掛け合わせると \[ a^2-2b^2 = x^2-2y^2 = 1\] となる. これと $\varepsilon$ の最小性により $a+b\sqrt 2 = 1$ が成り立つから, \[ x+y\sqrt 2 = \varepsilon ^n = x_n+y_n\sqrt 2\] が得られる. よって, \[ (y-y_n)\sqrt 2 = x_n-x\] であり, $x_n-x$ と $y-y_n$ は整数, $\sqrt 2$ は無理数であるから, $y-y_n = 0$ でなければならない. ゆえに, $(x,y) = (x_n,y_n)$ が成り立つ.
参考
- $d$ を平方数でない正の整数とする.
の形の方程式を「ペル方程式」(Pell's equation) と呼ぶ. さらに $d$ を $4$ で割った余りが $1$ であるとき,$x^2-dy^2 = 1,$ $x^2-dy^2 = -1,$ または $|x^2-dy^2| = 1$
の形の方程式も「ペル方程式」と呼ぶ.$x^2-dy^2 = 4,$ $x^2-dy^2 = -4,$ または $|x^2-dy^2| = 4$ - 方程式 $x^2-2y^2 = 1$ の意味づけについては, こちらを参照.
- 「ペル方程式」$|x^2-dy^2| = 1$ の正の整数解 $(x,y)$ のうち $y$ の値が $n$ 番目に小さいもの $(x,y) = (Q_n,P_n)$ (本問では $(x_n,y_n)$ で表した) について, $x$ 成分 $Q_n$ を「半同伴ペル数」(half-companion Pell number), $y$ 成分 $P_n$ を「ペル数」(Pell number) と呼ぶ. $\{ Q_n\}$ を「半同伴ペル数列」, $\{ P_n\}$ を「ペル数列」と呼ぶ.
- 「リュカ数」$L_n,$「フィボナッチ数」$F_n$ はそれぞれ「ペル方程式」 \[ |x^2-5y^2| = 4\] の正の整数解の $x$ 成分, $y$ 成分として定まる. そのため, $L_n,$ $F_n$ と $Q_n,$ $P_n$ の間には多くの類似が見られる.
- $|x^2-dy^2| = 1,$ $|x^2-dy^2| = 4$ のすべての整数解は $|x^2-dy^2| = 1,$ $|x^2-dy^2| = 4$ の非負整数解 $(x,y)$ を用いて $(\pm x,\pm y)$ (複号任意) の形に表される.
さらに, 次のことが知られている.
- (i)
- $d$ を $4$ で割った余りが $1$ であるとき.
$|x^2-dy^2| = 1$ のすべての整数解は $|x^2-dy^2| = 4$ の整数解で $x$ 成分, $y$ 成分が偶数であるもの $(x,y)$ を用いて $\left(\dfrac{x}{2},\dfrac{y}{2}\right)$ の形に表される.
また, $|x^2-dy^2| = 4$ のすべての正の整数解は正の整数解 $(x,y)$ で $x+y\sqrt d$ の値が最小であるもの $(x,y) = (x_1,y_1)$ から定まる実数 $\varepsilon = x_1+y_1\sqrt d$ を用いて
の形に表される. $x^2-dy^2 = -4$ の解が存在すれば, $x^2-dy^2 = 4$ の解は $n$ が偶数のときの解, $x^2-dy^2 = -4$ の解は $n$ が奇数のときの解である.$\left(\dfrac{\varepsilon ^n+\varepsilon '^n}{2},\dfrac{\varepsilon ^n-\varepsilon '^n}{2\sqrt d}\right)$ ($n$: 正の整数) - (ii)
- $d$ を $4$ で割った余りが $2,$ $3$ であるとき.
$|x^2-dy^2| = 1$ のすべての正の整数解は正の整数解 $(x,y)$ で $x+y\sqrt d$ の値が最小であるもの $(x,y) = (x_1,y_1)$ から定まる実数 $\varepsilon = x_1+y_1\sqrt d$ を用いて
の形に表される. $x^2-dy^2 = -1$ の解が存在すれば, $x^2-dy^2 = 1$ の解は $n$ が偶数のときの解, $x^2-dy^2 = -1$ の解は $n$ が奇数のときの解である.$\left(\dfrac{\varepsilon ^n+\varepsilon '^n}{2},\dfrac{\varepsilon ^n-\varepsilon '^n}{2\sqrt d}\right)$ ($n$: 正の整数)
問題《解をもたないペル方程式》
方程式 $x^2-3y^2 = -1$ の整数解は存在しないことを示せ.
解答例
$x,$ $y$ を整数とする.
- (i)
- $x = 3d$ ($d$: 整数) のとき. \[ x^2-3y^2 = (3d)^2-3y^2 = 3(3d^2-y^2)\] ($3d^2-y^2$ は整数) は $3$ で割り切れるから, $x^2-3y^2 \neq -1$ である.
- (ii)
- $x = 3d\pm 1$ ($d$: 整数) のとき. \[ x^2-3y^2 = (3d\pm 1)^2-3y^2 = 3(3d^2\pm 2d-y^2)+1\] ($3d^2\pm 2d-y^2$ は整数) を $3$ で割った余りは $1$ であり, $-1$ を $3$ で割った余りは $2$ であるから, $x^2-3y^2 \neq -1$ である.
参考
$d$ を平方数でない正の整数とする.
- $x^2-dy^2 = 1$ または $x^2-dy^2 = -1$ の形の方程式を「ペル方程式」(Pell's equation) と呼ぶ.
- $x^2-dy^2 = 1$ は, $d$ の値によらず無限に多くの整数解をもつことが知られている.
- 正方形の隊列に $1$ 人を加えて隊列を組み直すとき, 同じ大きさの正方形の隊列が $2$ 個作れることはあるが ($1^2+1 = 2\cdot 1^2,$ $7^2+1 = 2\cdot 5^2$ など), 同じ大きさの正方形の隊列が $3$ 個作れることはない ($x^2+1 = 3y^2$ は整数解をもたない). つまり, $x^2-dy^2 = -1$ は $d$ の値によって, 無限に多くの整数解をもつこともあれば, 全く整数解をもたないこともある.
問題《円周の方程式の有理数解》
$x^2+y^2 = 3$ の有理数解は存在しないことを示せ.
解答例
$x = \dfrac{a}{c},$ $y = \dfrac{b}{c}$ ($a,$ $b,$ $c$: 整数, $c > 0$) のとき,
\[ x^2+y^2 = 3 \iff a^2+b^2 = 3c^2\ \cdots [1]\]
であるから, $[1]$ の整数解が存在しても $a,$ $b,$ $c$ は互いに素でないことを示す.
- (i)
- $a,$ $b$ の少なくとも一方が $3$ の倍数のとき. $a$ が $3$ の倍数であるとしてよい. このとき, $b^2 = 3c^2-a^2$ は $3$ の倍数であるから, $b$ は $3$ の倍数である. よって, $3c^2 = a^2+b^2$ は $9$ の倍数であるから, $c^2$ は $3$ の倍数で, $c$ は $3$ の倍数である. したがって, $[1]$ の整数解は互いに素でない.
- (ii)
- $a = 3d\pm 1,$ $b = 3e\pm 1$ ($d,$ $e$: 整数, 複号任意) のとき. \[\begin{aligned} a^2+b^2 &= (3d\pm 1)^2+(3e\pm 1)^2 \\ &= 3(3d^2+3e^2\pm 2d\pm 2e)+2 \end{aligned}\] (かっこ内は整数) は $3$ で割り切れない. よって, $[1]$ の整数解は存在しない.
参考
一般に, $ax^2+by^2 = c$ ($a,$ $b,$ $c$: $0$ でない有理数) は無限に多くの有理数解をもつか, 全く有理数解をもたないかのいずれかであることが知られている.
これは, $1$ 個でも $ax^2+by^2 = c$ の有理数解 $(x,y) = (x_0,y_0)$ が存在すれば, 点 $(x_0,y_0)$ を通る傾きが有理数の直線と曲線 $ax^2+by^2 = c$ の交点の各座標が有理数になることからわかる.
問題《周長と面積が等しい直角三角形》
$3$ 辺の長さが整数であり, 周の長さと面積が等しい直角三角形はちょうど $2$ 個存在する.
それらの $3$ 辺の長さを求めよ.
解答例
直角を挟む $2$ 辺の長さが整数 $x,$ $y$ $(x \leqq y),$ 斜辺の長さが整数 $z$ の直角三角形において, 周の長さと面積が等しいとする.
このとき,
\[\begin{aligned}
x^2+y^2 &= z^2 \quad \cdots [1], \\
x+y+z &= \frac{xy}{2} \quad \cdots [2]
\end{aligned}\]
が成り立つ.
$[2]$ から得られる $2z = xy-2(x+y)$ を $[1]\times 4$ に代入すると,
\[\begin{aligned}
4(x^2+y^2) &= \{ xy-2(x+y)\} ^2 \\
&= x^2y^2-4xy(x+y)+4(x+y)^2 \\
&= x^2y^2-4xy(x+y)+4(x^2+2xy+y^2) \\
0 &= x^2y^2-4xy(x+y)+8xy \\
&= xy(xy-4x-4y+8)
\end{aligned}\]
が得られる.
$x,$ $y > 0$ であるから,
\[\begin{aligned}
xy-4x-4y+8 &= 0 \\
(x-4)(y-4) &= 8
\end{aligned}\]
が成り立つ.
$x-4,$ $y-4$ は整数で $-4 < x-4 \leqq y-4$ であるから,
\[\begin{aligned}
(x-4,y-4) &= (1,8),\ (2,4) \\
(x,y) &= (5,12),\ (6,8)
\end{aligned}\]
である.
$(x,y) = (5,12)$ のとき $z = 13,$ $(x,y) = (6,8)$ のとき $z = 10$ であるから, 求める直角三角形の $3$ 辺の長さは
\[ (5,12,13),\ (6,8,10)\]
である.
参考
高次不定方程式
問題《非自明な平方四角錐数》
方程式
\[ y^2 = \frac{1}{6}x(x+1)(2x+1) \quad \cdots [*]\]
の正の整数解 $(x,y)$ について, 次の問いに答えよ.
- (1)
- $x,$ $x+1,$ $2x+1$ はどの $2$ つも互いに素であることを示せ.
- (2)
- $5$ 以上の各素数 $p$ に対して, $x,$ $x+1,$ $2x+1$ が $p$ で割り切れる回数はいずれも偶数 ($0$ を含む) であることを示せ.
- (3)
- $[*]$ の $(x,y) = (1,1)$ 以外の正の整数解で $x$ が最小のものを求めよ.
(参考:『新しいカギ』「第 $1$ 回高校生クイズ何問目」決勝 $2$ 問目)
解答例
- (1)
- $x+1,$ $2x+1$ を $x$ で割った余りは $1$ であるから, $x$ と $x+1,$ $x$ と $2x+1$ は互いに素である. また, $-(2x+1) = -2(x+1)+1$ を $x+1$ で割った余りは $1$ であるから, $x+1$ と $-(2x+1)$ は互いに素であり, よって $x+1$ と $2x+1$ は互いに素である.
- (2)
- $[*]$ は \[ 6y^2 = x(x+1)(2x+1)\] と同値である. $5$ 以上の各素数 $p$ に対して, $6y^2$ つまり $x(x+1)(2x+1)$ が $p$ で割り切れる回数は偶数であり, (1) の結果から $x,$ $x+1,$ $2x+1$ のうち高々 $1$ つしか $p$ で割り切れないので, $x,$ $x+1,$ $2x+1$ が $p$ で割り切れる回数はいずれも偶数である.
- (3)
- $(x,y)$ を $[*]$ の正の整数解とする.
(2) の結果から, $x,$ $x+1,$ $2x+1$ が $5$ 以上の素数で割り切れる回数が奇数になることはない.
- $x = 5,$ $7,$ $10,$ $11,$ $13,$ $14,$ $15,$ $17,$ $19,$ $20,$ $21,$ $22,$ $23$ は, $x$ が $5$ 以上の素数で割り切れる回数が奇数になることがあるから, 不適.
- $x = 4,$ $6,$ $9,$ $12,$ $16,$ $18$ は, それぞれ $x+1 = 5,$ $7,$ $10,$ $13,$ $17,$ $19$ が $5$ 以上の素数で割り切れる回数が奇数になることがあるから, 不適.
- $x = 2,$ $3,$ $8$ は, それぞれ $2x+1 = 5,$ $7,$ $17$ が $5$ 以上の素数であるから, 不適.
- $\dfrac{1}{6}\cdot 24\cdot 25\cdot (2\cdot 24+1) = 4900 = 70^2$ であるから, $(x,y) = (24,70)$ は $[*]$ を満たす.
参考
- 正の整数 $x,$ $y$ を用いて $N = \dfrac{1}{6}x(x+1)(2x+1) = y^2$ の形に表される正の整数 $N$ は, $x$ 段の正四角錐状にも $y$ 行 $y$ 列の正方形状にも並べられるような球の個数であるから,「平方四角錐数」と呼ばれる. $y^2 = \dfrac{1}{6}x(x+1)(2x+1)$ が $(x,y) = (1,1),$ $(24,70)$ 以外の正の整数解をもつか, つまり「平方四角錐数」が $1,$ $4900$ のみであるかという「リュカのキャノンボール問題」(Lucas' cannonball problem) は, $1918$ 年に肯定的に解決された.
- $f(x) = 0$ が重解をもたないような $3$ 次多項式 $f(x)$ を用いて $y^2 = f(x)$ で定義される曲線は, 「楕円曲線」(elliptic curve) と呼ばれ, 現代整数論の主要な研究対象である. この形の方程式は有理数係数の場合に高々有限個の整数解しかもたないという「ジーゲルの定理」(Siegel's theorem) が知られている.
問題《フェルマー予想の $n = 4$ の場合》
$x^4+y^4 = z^4$ を満たす正の整数 $x,$ $y,$ $z$ は存在しないという定理を証明したい.
- (1)
- $16a^4+b^4 = c^2$ を満たし, $2a,$ $b,$ $c$ が互いに素であるような正の整数 $a,$ $b,$ $c$ が存在しないことを示せば, 定理が証明されることを示せ.
- (2)
- $2a,$ $c$ も互いに素であることを示せ.
- (3)
- $c+4a^2 = m^4,$ $c-4a^2 = n^4$ を満たす互いに素な正の奇数 $m,$ $n$ が存在することを示せ.
- (4)
- (3) の $m,$ $n$ について, $m+n = 2s,$ $m-n = 2t$ ($s,$ $t$: 整数) とする. $s,$ $t$ を用いて $a^2$ を表せ.
- (5)
- $a = 2a_1b_1c_1,$ $16a_1{}^4+b_1{}^4 = c_1{}^2$ を満たし, $2a_1,$ $b_1,$ $c_1$ が互いに素であるような正の整数 $a_1,$ $b_1,$ $c_1$ が存在することを示せ.
- (6)
- (5) までの議論から矛盾を導くことで, 定理の証明を完成せよ.
(参考: $2010$ 福島県立医科大)
解答例
- (1)
- すべての整数 $n$ は $n = 2q$ または $n = 2q+1$ ($q$: 整数) の形に表され, \[ (2q)^2 = 4q^2, \quad (2q+1)^2 = 4(q^2+q)+1\] が成り立つから, $n^2$ を $4$ で割った余りは $0$ または $1$ である (前者は $n$ が偶数のとき, 後者は $n$ が奇数のとき). 正の整数 $x,$ $y,$ $z$ に対して, $x^4,$ $y^4,$ $z^4$ は平方数であるから, $x^4+y^4 = z^4$ が成り立つためには, $x^4,$ $y^4$ を $4$ で割った余りの組合せが $\{ 0,0\}$ または $\{ 0,1\}$ であること, つまり $x,$ $y$ の少なくとも一方が偶数であることが必要である. ここで, $x^4+y^4 = z^4$ の両辺を $x,$ $y,$ $z$ の最大公約数の $4$ 乗で割ると, $x,$ $y,$ $z$ が互いに素である場合に置き換えられる. このとき, $x$ が偶数, $y$ が奇数であるとしても一般性を失わないから, その場合に $a = \dfrac{x}{2},$ $b = y,$ $c = z^2$ とおくと, $16a^4+b^4 = c^2$ を満たし, $2a,$ $b,$ $c$ が互いに素であるような正の整数 $a,$ $b,$ $c$ が得られる. よって, このような正の整数 $a,$ $b,$ $c$ が存在しないことを示せば, 定理が証明される.
- (2)
- $2a,$ $c$ の共通の素因数 $p$ の存在を仮定する.
このとき, $2a = pa',$ $c = pc'$ ($a',$ $c'$: 整数) とすると,
\[ b^4 = c^2-16a^4 = (pc')^2-(pa')^4 = p^2(c'^2-p^2a'^4)\]
となる.
ここで, $b^4$ は $p^2$ の倍数であるから, $b^2$ は $p$ の倍数であり, よって $b$ は $p$ の倍数であるが,
これは $2a,$ $b,$ $c$ が互いに素であることに反する.
よって, $2a,$ $c$ も互いに素である. - (3)
- $16a^4+b^4 = c^2$ から, \[ b^4 = c^2-16a^4 = (c+4a^2)(c-4a^2)\] が成り立つ. $c+4a^2,$ $c-4a^2$ の最大公約数を $g$ とおく. さらに, $c+4a^2 = gx,$ $c-4a^2 = gy$ ($x,$ $y$: 整数) とする. $c$ は奇数, $4a^2$ は偶数であるから $g,$ $x,$ $y$ はすべて奇数であるので, $x+y,$ $x-y$ は偶数であり, よって \[ c = g\cdot\frac{x+y}{2}, \quad 4a^2 = g\cdot\frac{x-y}{2}\] は $g$ の倍数である. このことと (2) の結果から $g = 1$ であるので, \[ c+4a^2 = m^4 \quad \cdots [1], \quad c-4a^2 = n^4 \quad \cdots [2]\] を満たす互いに素な正の奇数 $m,$ $n$ が存在する.
- (4)
- $m+n = 2s,$ $m-n = 2t$ から, \[ m = s+t, \quad n = s-t\] である. $[1],$ $[2]$ の辺々を引くと, \[\begin{aligned} 8a^2 &= m^4-n^4 = (m^2+n^2)(m+n)(m-n) \\ &= \{ (s+t)^2+(s-t)^2\}\cdot 2s\cdot 2t \\ &= 8st(s^2+t^2) \\ a^2 &= st(s^2+t^2) \quad \cdots [3] \end{aligned}\] が得られる.
- (5)
- $m = s+t,$ $n = s-t$ が互いに素であることから $s,$ $t$ は互いに素であり, よって $s,$ $t,$ $s^2+t^2$ のどの $2$ つも互いに素である. さらに, $m = s+t,$ $n = s-t$ は奇数であるから, $s,$ $t$ の一方は偶数, 他方は奇数であり, よって $s^2+t^2$ は奇数である. よって, $[3]$ から, $2a_1,$ $b_1,$ $c_1$ が互いに素であるような正の整数 $a_1,$ $b_1,$ $c_1$ を用いて $\{ s,t\} = \{ (2a_1)^2,b_1{}^2\},$ $s^2+t^2 = c_1{}^2$ とおけて, \[\begin{aligned} &a^2 = (2a_1)^2b_1{}^2c_1{}^2, \quad a = 2a_1b_1c_1, \\ &16a_1{}^4+b_1{}^4 = c_1{}^2 \end{aligned}\] となる.
- (6)
- $a_1,$ $b_1,$ $c_1$ に (5) の結果を適用すると, $a_1 = 2a_2b_2c_2,$ $16a_2{}^4+b_2{}^4 = c_2{}^2$ を満たし, $2a_2,$ $b_2,$ $c_2$ が互いに素であるような正の整数 $a_2,$ $b_2,$ $c_2$ が得られる.
これを続けると, $a > a_1 > \cdots > a_n > \cdots$ を満たす正の整数 $a_1,$ $\cdots,$ $a_n,$ $\cdots$ が得られるが, これは $a$ 未満の正の整数が有限個しかないことに反する.
ゆえに, 定理が成り立つ.
参考
- フェルマーが証明を書くには余白が狭すぎると述べた, $3$ 以上の整数 $n$ に対して $x^n+y^n = z^n$ は正の整数解をもたないという定理は, 長らく「フェルマー予想」(Fermat conjecture) または「フェルマーの最終定理」と呼ばれていたが, $20$ 世紀末にワイルズらによって証明された ($n = 3,$ $4$ の場合は個別に証明される).
- (6) のように, 条件を満たすより小さい整数を次々と作って矛盾を導く論法は, 「無限降下法」(infinite descent) と呼ばれる.
分数型の不定方程式
問題《エジプト分数に関する不定方程式》
- (A)
- \[\frac{1}{x}+\frac{1}{y} = 1\ \cdots [1], \quad 0 < x < y\ \cdots [2]\] の整数解は存在しないことを示せ.
- (B)
- \[\frac{1}{x}+\frac{1}{y}+\frac{1}{z} = 1\ \cdots [1], \quad 0 < x < y < z\ \cdots [2]\] の整数解をすべて求めよ.
解答例
- (A)
- $x,$ $y > 0$ のとき \[\begin{aligned} [1] &\iff y+x = xy \iff xy-x-y+1 = 1 \\ &\iff (x-1)(y-1) = 1 \\ &\iff x-1 = y-1 = 1 \iff x = y = 2 \end{aligned}\] であるから, $[1],$ $[2]$ の整数解は存在しない.
- (B)
- 整数 $x,$ $y,$ $z$ が $[1],$ $[2]$ を満たすとする. $y,$ $z > 0$ から $\dfrac{1}{y}+\dfrac{1}{z} > 0$ であるので, $x = 1$ は不適で, $x \geqq 2$ である. また, $[1],$ $[2]$ から \[ 1 = \dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z} < \frac{1}{x}+\frac{1}{x}+\frac{1}{x} = \frac{3}{x}\] であるので, $x < 3$ である. よって, $x = 2$ である. $[2]$ から $0 = x-2 < y-2 < z-2$ であることに注意すると, \[\begin{aligned} [1] &\iff \frac{1}{2}+\frac{1}{y}+\frac{1}{z} = 1 \iff \frac{1}{y}+\frac{1}{z} = \frac{1}{2} \\ &\iff 2z+2y = yz \iff yz-2y-2z+4 = 4 \\ &\iff (y-2)(z-2) = 4 \\ &\iff (y-2,z-2) = (1,4) \iff (y,z) = (3,6) \end{aligned}\] となる. ゆえに, 求める整数解は, $(x,y,z) = (2,3,6)$ である.
参考
- 古代エジプトでは, 整数でない有理数を表すとき, $\dfrac{2}{3}$ を唯一の例外として, 相異なる「単位分数」(分子が $1$ の分数) の和として表した. このように表された有理数を「エジプト分数」と呼ぶ. 「エジプト分数」は, 中世までヨーロッパで広く使われていた.
- 真分数 $\dfrac{m}{n}$ ($m,$ $n$: 互いに素な正の整数, $m < n$) について, $n$ を $m$ で割ったときの商を $q,$ 余りを $r$ とすると \[\frac{m}{n} = \frac{1}{q+1}+\frac{m-r}{n(q+1)}, \quad 0 < m-r < m\] となるから, この操作を高々 $m$ 回繰り返すことにより, $\dfrac{m}{n}$ を「エジプト分数」として表せる (こちらを参照).
- $\dfrac{5}{6} = \dfrac{1}{2}+\dfrac{1}{3} = \dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{12}$ のように,「エジプト分数」による表し方は一意的でない.
- 本問では,「エジプト分数」による $1$ の表示で項数が最小のものを決定した.
問題《$1$ 種類の正多角形による平面充填形》
$1$ 種類の合同な正 $p$ 角形で平面を隙間も重なりもなく敷き詰めて, 各頂点で $q$ 個の正 $p$ 角形の辺が同じ形状で交わるようにする.
このとき, 考えられる整数 $p,$ $q$ の値の組をすべて求めよ.
解答例
$1$ つの頂点に集まる角の和は $360^\circ$ であり, 正 $p$ 角形の内角の大きさは $180^\circ\times (p-2)\div p$ であるから,
\[\frac{180(p-2)q}{p} = 360\]
が成り立つ.
整理すると,
\[\begin{aligned}
(p-2)q &= 2p \\
pq-2p-2q &= 0 \\
(p-2)(q-2) &= 4
\end{aligned}\]
となる.
$p \geqq 3,$ $q \geqq 3$ から $p-2 \geqq 1,$ $q-2 \geqq 1$ であることに注意すると,
\[\begin{aligned}
(p-2,q-2) &= (1,4),\ (2,2),\ (4,1) \\
(p,q) &= (3,6),\ (4,4),\ (6,3)
\end{aligned}\]
が得られる.
参考
- 有限種類の合同な図形で平面を隙間も重なりもなく敷き詰めることを「平面充填」(tessellation) と呼ぶ. 敷き詰めに使われる平面図形を「タイル」(tile) と呼び,「タイル」で敷き詰められた平面を「平面充填形」(tessellation) と呼ぶ. 与えられた「タイル」を使った「平面充填形」が存在するとき, それらの「タイル」は「平面充填可能」であるという.
- ピタゴラスは, $1$ 種類の正多角形を「タイル」とする「平面充填形」($3$ 枚以上の「タイル」は頂点のみを共有するもの) は正三角形, 正方形, 正六角形を使う $3$ パターンに限ることを証明した.
これらの「平面充填形」を「正平面充填形」(regular tessellation) と呼ぶ.
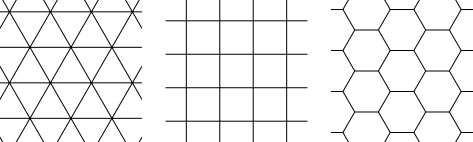
- 任意の三角形, 四角形は「平面充填可能」である.
- 「平面充填可能」な凸五角形は現在までに $15$ 種類発見されている.
- 「平面充填可能」な凸六角形は全部で $3$ 種類あることが知られている.
- $7$ 本以上の辺をもつ凸多角形は「平面充填可能」でないことが知られている.
問題《多種類の正多角形による平面充填形》
$1$ 辺の長さが等しい正 $p_1$ 角形, $\cdots,$ 正 $p_r$ 角形 $(p_1 \leqq \cdots \leqq p_r)$ で平面を隙間も重なりもなく敷き詰めて, 各頂点でこれら $r$ 個の正多角形の辺が同じ形状で交わるようにする.
ただし, これら $r$ 個の中に互いに合同な正多角形が含まれていてもよいとする.
- (1)
- \[\frac{1}{p_1}+\cdots +\frac{1}{p_r} = \frac{r}{2}-1\] が成り立つことを示せ.
- (2)
- $3 \leqq r \leqq 6$ であることを示せ.
- (3)
- (1), (2) と次の条件 (A), (B) から考えられる整数 $p_1,$ $\cdots,$ $p_r$ の値の組をすべて求めよ (解答では正 $p_1$ 角形, $\cdots,$ 正 $p_r$ 角形が実際に平面に敷き詰められるかどうかを確かめなくてもよいとする).
- (A)
- $r = 3$ のとき, $p_1,$ $p_2,$ $p_3$ はすべて偶数であるか, $p_1,$ $p_2,$ $p_3$ のうち $1$ つが奇数であれば残り $2$ つは等しい偶数である.
- (B)
- $r = 4$ のとき, $(p_1,p_2,p_3,p_4) = (3,3,4,12)$ となることはない.
(参考: $2017$ 名古屋大)
(参考文献: 一松信,『正多面体を解く』, 東海大学出版部, $2002$)
(参考文献: 一松信,『正多面体を解く』, 東海大学出版部, $2002$)
解答例
- (1)
- $1$ つの頂点に集まる角の和は $360^\circ$ であり, 正 $p_k$ 角形の内角の大きさは $180^\circ\times (p_k-2)\div p_k$ であるから, \[\frac{180(p_1-2)}{p_1}+\cdots +\frac{180(p_r-2)}{p_r} = 360\] が成り立つ. 整理すると, \[\begin{aligned} \frac{p_1-2}{2p_1}+\cdots +\frac{p_r-2}{2p_r} &= 1 \\ \left(\frac{1}{2}-\frac{1}{p_1}\right) +\cdots +\left(\frac{1}{2}-\frac{1}{p_r}\right) &= 1 \\ \frac{1}{p_1}+\cdots +\frac{1}{p_r} &= \frac{r}{2}-1 \quad \cdots [*] \end{aligned}\] となる.
- (2)
- 正多角形の内角の大きさは $180^\circ$ 未満であるから $r \leqq 2$ となることはなく, $r \geqq 3$ である. また, $3 \leqq p_1 \leqq \cdots \leqq p_r$ から, \[\begin{aligned} \frac{1}{p_1}+\cdots +\frac{1}{p_r} &\leqq r\cdot\frac{1}{3} \\ \frac{r}{2}-1 &\leqq r\cdot\frac{1}{3} \quad (\because [*]) \\ 3r-6 &\leqq 2r \\ r &\leqq 6 \end{aligned}\] が成り立つ. よって, $3 \leqq r \leqq 6$ である.
- (3)
- (I)
- $r = 3$ のとき.
\[ [*] \iff \frac{1}{p_1}+\frac{1}{p_2}+\frac{1}{p_3} = \frac{1}{2} \quad \cdots [1]\]
である.
$p_1 \leqq p_2 \leqq p_3$ から,
\[\begin{aligned}
\frac{1}{2} &\leqq 3\cdot\frac{1}{p_1} \\
p_1 &\leqq 6
\end{aligned}\]
である.
- (i)
- $p_1 = 3$ のとき. 条件 (A) から $p_2 = p_3$ であるので, $[1]$ から \[\begin{aligned} \frac{1}{3}+2\cdot\frac{1}{p_2} &= \frac{1}{2} \\ p_2 = p_3 &= 12 \end{aligned}\] が得られる.
- (ii)
- $p_1 = 4$ のとき. $[1]$ を整理すると, \[\begin{aligned} \frac{1}{p_2}+\frac{1}{p_3} &= \frac{1}{4} \\ p_2p_3-4p_2-4p_3 &= 0 \\ (p_2-4)(p_3-4) &= 16 \end{aligned}\] となる. $4 \leqq p_2 \leqq p_3$ から $0 \leqq p_2-4 \leqq p_3-4$ であることに注意すると, \[\begin{aligned} (p_2-4,p_3-4) &= (1,16),\ (2,8),\ (4,4) \\ (p_2,p_3) &= (5,20),\ (6,12),\ (8,8) \end{aligned}\] が得られる. このうち, 条件 (A) を満たすのは, $(p_2,p_3) = (6,12),$ $(8,8)$ である.
- (iii)
- $p_1 = 5$ のとき. 条件 (A) から $p_2 = p_3$ であるので, $[1]$ から \[\begin{aligned} \frac{1}{5}+2\cdot\frac{1}{p_2} &= \frac{1}{2} \\ p_2 = p_3 &= \frac{3}{20} \end{aligned}\] が得られる. これは $p_2,$ $p_3$ が整数であることに反する.
- (iv)
- $p_1 = 6$ のとき. $[1]$ を整理すると, \[\begin{aligned} \frac{1}{p_2}+\frac{1}{p_3} &= \frac{1}{3} \\ p_2p_3-3p_2-3p_3 &= 0 \\ (p_2-3)(p_3-3) &= 9 \end{aligned}\] となる. $6 \leqq p_2 \leqq p_3$ から $3 \leqq p_2-3 \leqq p_3-3$ であることに注意すると, \[\begin{aligned} (p_2-3,p_3-3) &= (3,3) \\ (p_2,p_3) &= (6,6) \end{aligned}\] が得られる. これは (A) を満たす.
- (II)
- $r = 4$ のとき.
\[ [*] \iff \frac{1}{p_1}+\frac{1}{p_2}+\frac{1}{p_3}+\frac{1}{p_4} = 1 \quad \cdots [2]\]
である.
$p_1 \leqq p_2 \leqq p_3 \leqq p_4$ から,
\[\begin{aligned}
1 &\leqq 4\cdot\frac{1}{p_1} \\
p_1 &\leqq 4
\end{aligned}\]
である.
- (i)
- $p_1 = 3$ のとき.
\[ [2] \iff \frac{1}{p_2}+\frac{1}{p_3}+\frac{1}{p_4} = \frac{2}{3} \quad \cdots [2]'\]
である.
$p_2 \leqq p_3 \leqq p_4$ から,
\[\begin{aligned}
\frac{2}{3} &\leqq 3\cdot\frac{1}{p_2} \\
p_2 &\leqq \frac{9}{2} \\
p_2 &= 3,\ 4
\end{aligned}\]
である.
- $p_2 = 3$ のとき. $[2]'$ を整理すると, \[\begin{aligned} \frac{1}{p_3}+\frac{1}{p_4} &= \frac{1}{3} \\ p_3p_4-3p_3-3p_4 &= 0 \\ (p_3-3)(p_4-3) &= 9 \end{aligned}\] となる. $3 \leqq p_3 \leqq p_4$ から $0 \leqq p_3-3 \leqq p_4-3$ であることに注意すると, \[\begin{aligned} (p_3-3,p_4-3) &= (1,9),\ (3,3) \\ (p_3,p_4) &= (4,12),\ (6,6) \end{aligned}\] が得られる. このうち, 条件 (B) を満たすのは, $(p_3,p_4) = (6,6)$ である.
- $p_2 = 4$ のとき. $[2]'$ を整理すると, \[\frac{1}{p_3}+\frac{1}{p_4} = \frac{5}{12}\] となる. $4 \leqq p_3 \leqq p_4$ から $4 \leqq p_3 \leqq \dfrac{24}{5}$ であることに注意すると, \[ (p_3,p_4) = (4,6)\] が得られる. これは条件 (B) を満たす.
- (ii)
- $p_1 = 4$ のとき. $[2]$ から \[\frac{1}{p_2}+\frac{1}{p_3}+\frac{1}{p_4} = \frac{3}{4}\] であるので, $p_2 \leqq p_3 \leqq p_4$ から \[\begin{aligned} \frac{3}{4} &\leqq 3\cdot\frac{1}{p_2} \\ p_2 &\leqq 4 \\ p_2 &= 4 \end{aligned}\] である. よって, \[\begin{aligned} \frac{1}{p_3}+\frac{1}{p_4} &= \frac{1}{2} \\ p_3p_4-2p_3-2p_4 &= 0 \\ (p_3-2)(p_4-2) &= 4 \end{aligned}\] となる. $4 \leqq p_3 \leqq p_4$ から $2 \leqq p_3-2 \leqq p_4-2$ であることに注意すると, \[\begin{aligned} (p_3-2,p_4-2) &= (2,2) \\ (p_3,p_4) &= (4,4) \end{aligned}\] が得られる. これは条件 (B) を満たす.
- (III)
- $r = 5$ のとき. \[ [*] \iff \frac{1}{p_1}+\frac{1}{p_2}+\frac{1}{p_3}+\frac{1}{p_4}+\frac{1}{p_5} = \frac{3}{2} \quad \cdots [3]\] である. $p_1 \leqq p_2 \leqq p_3 \leqq p_4 \leqq p_5$ から, \[\begin{aligned} \frac{3}{2} &\leqq 5\cdot\frac{1}{p_1} \\ p_1 &\leqq \frac{10}{3} \\ p_1 &= 3 \end{aligned}\] である. $[3]$ から \[\frac{1}{p_2}+\frac{1}{p_3}+\frac{1}{p_4}+\frac{1}{p_5} = \frac{7}{6} \quad \cdots [3]'\] であるので, $p_2 \leqq p_3 \leqq p_4 \leqq p_5$ から \[\begin{aligned} \frac{7}{6} &\leqq 4\cdot\frac{1}{p_2} \\ p_2 &\leqq \frac{24}{7} \\ p_2 &= 3 \end{aligned}\] である. $[3]'$ から \[\frac{1}{p_3}+\frac{1}{p_4}+\frac{1}{p_5} = \frac{5}{6} \quad \cdots [3]''\] であるので, $p_3 \leqq p_4 \leqq p_5$ から \[\begin{aligned} \frac{5}{6} &\leqq 3\cdot\frac{1}{p_3} \\ p_3 &\leqq \frac{18}{5} \\ p_3 &= 3 \end{aligned}\] である. $[3]''$ を整理すると, \[\begin{aligned} \frac{1}{p_4}+\frac{1}{p_5} &= \frac{1}{2} \\ p_4p_5-2p_4-2p_5 &= 0 \\ (p_4-2)(p_5-2) &= 4 \end{aligned}\] となる. $3 \leqq p_4 \leqq p_5$ から $1 \leqq p_4-2 \leqq p_5-2$ であることに注意すると, \[\begin{aligned} (p_4-2,p_5-2) &= (1,4),\ (2,2) \\ (p_4,p_5) &= (3,6),\ (4,4) \end{aligned}\] が得られる.
- (IV)
- $r = 6$ のとき. \[ [*] \iff \frac{1}{p_1}+\cdots +\frac{1}{p_6} = 2\] である. ここで, $3 \leqq p_1 \leqq \cdots \leqq p_6$ から $\dfrac{1}{p_k} \leqq \dfrac{1}{3}$ であり, $6\cdot\dfrac{1}{3} = 2$ であるので, \[ (p_1,p_2,p_3,p_4,p_5,p_6) = (3,3,3,3,3,3)\] である.
参考
- 上記の解のうち $3$ つは「正平面充填形」を表す.
- $1$ 辺の長さが等しい複数種類の正多角形を「タイル」とする「平面充填形」は,「準正平面充填形」(semiregular tessellation) または「アルキメデスの平面充填形」(Archimedean tessellation) と呼ばれ, 全部で $8$ パターンある. このうちの $2$ パターンは, 各頂点の周りに順に, 正三角形 $3$ 枚, 正方形 $2$ 枚が集まる「平面充填形」と, 正三角形 $2$ 枚, 正方形 $1$ 枚, 正三角形 $1$ 枚, 正方形 $1$ 枚が集まる「平面充填形」である.
指数関数を含む不定方程式
問題《カタラン予想に関する方程式》
- (A)
- $x^2-2^n = 1$ を満たす正の整数 $x,$ $n$ の組をすべて求めよ.
- (B)
- $3^m-y^3 = 1$ を満たす正の整数 $m,$ $y$ の組をすべて求めよ.
($2017$ オリジナル)
- (C)
- $3^m-2^n = 1$ を満たす正の整数 $m,$ $n$ の組をすべて求めよ.
ヒント: $n > 1$ ならば, $m$ は偶数である.
(参考: $2018$ 東北大)
解答例
- (A)
- 正の整数 $x,$ $n$ が $x^2-2^n = 1$ を満たすとする. これは \[ x^2 = 2^n+1\] と変形できるから, $x$ は奇数でなければならない. よって, $x = 2d-1$ ($d$: 正の整数) とおける. このとき, \[ 2^n = (2d-1)^2-1 = 4d(d-1)\] となる. したがって, $n \geqq 2$ である. 両辺を $4$ で割って得られる \[ 2^{n-2} = d(d-1)\] は, $d = 2$ のとき解 $n = 3$ をもつが, $d = 1$ のとき左辺が正であることから解をもたず, $d \geqq 3$ のとき $d(d-1)$ が奇数の素因数をもつことから解をもたない (左辺は $2$ の累乗であるから, 右辺の各因数は $2$ の累乗か $1$ でなければならない). ゆえに, 求める解は $(x,n) = (3,3)$ である.
- (B)
- 正の整数 $m,$ $y$ が $3^m-y^3 = 1$ を満たすとする. これは \[ y^3 = 3^m-1\] と変形できるから, $y$ を $3$ で割った余りは $2$ である(実際, $y$ が $3$ の倍数のとき $y^3$ を $3$ で割った余りは $0$ になり, $y =3d+1$ ($d$: 非負整数)のとき $y^3 = 3(9d^3+9d^2+3d)+1$ を $3$ で割った余りは $1$ になってしまうからである). よって, $y = 3d-1$ ($d$: 正の整数) とおける. このとき, \[ 3^m = (3d-1)^3+1 = 9d(3d^2-3d+1)\] となる. したがって, $m \geqq 2$ である. 両辺を $9$ で割って得られる \[ 3^{m-2} = d(3d^2-3d+1)\] は, $d = 1$ のとき解 $m = 2$ をもつが, $d > 1$ のとき $3d^2-3d+1$ が $3$ の倍数でも $1$ でもないことから解をもたない (左辺は $3$ の累乗であるから, 右辺の各因数は $3$ の累乗か $1$ でなければならない). ゆえに, 求める解は $(m,y) = (2,2)$ である.
- (C)
- まず, $n > 1$ ならば, $m$ は偶数であることを示す.
$n$ は整数であるから, $n > 1$ のとき, $n \geqq 2$ である.
このとき, 仮に $m$ が奇数であるとすると, $m = 2k+1$ ($k$: 非負整数) と書けて,
\[\begin{aligned}
3^m-2^n &= 3^{2k+1}-2^n = 3\cdot 9^k-4\cdot 2^{n-2} \\
&\equiv 3\cdot 1^k = 3 \pmod 4
\end{aligned}\]
となってしまうから, $m$ は偶数である.
これをもとにして, $3^m-2^n = 1$ を満たす正の整数 $m,$ $n$ の組を求める.- (i)
- $n = 1$ のとき. $(m,n) = (1,1)$ は $[\ast ]$ を満たす.
- (ii)
- $n > 1$ のとき. $m$ は偶数であるので, $m = 2k$ ($m$: 正の整数) と書けて \[\begin{aligned} [\ast ] &\iff 3^{2k}-1 = 2^n \\ &\iff (3^k+1)(3^k-1) = 2^n \end{aligned}\] となる. よって, ある非負整数 $i,$ $j$ に対して \[ 3^k+1 = 2^i, \quad 3^k-1 = 2^j, \quad i+j = n\] となり, 第 $1$ 式から第 $2$ 式を引くと \[ 2^i-2^j = (3^k+1)-(3^k-1)\] から \[ 2^j(2^{i-j}-1) = 2\] となるので, $j = i-j = 1$ から $(i,j) = (2,1)$ となる. このとき, $(m,n) = (2,3)$ である.
参考
「カタラン方程式」と呼ばれる方程式 $x^m-y^n = 1$ の $x,$ $y > 0,$ $m,$ $n > 1$ なる整数解は $(x,m,y,n) = (3,2,2,3)$ に限る,
つまり差が $1$ であるような正の累乗数は $9$ と $8$ のみであるというのが有名な「カタラン予想」(Catalan's conjecture) で,
2002 年に P・ミハイレスクによって肯定的に解決された.
問題《イェスマノヴィッチ予想に関する方程式》
正の整数 $x,$ $y,$ $z$ が
\[ 3^x+4^y = 5^z\]
を満たすとする.
- (1)
- $x$ は偶数であることを示せ.
- (2)
- $z$ は偶数であることを示せ.
- (3)
- $5^{\frac{z}{2}}+3^{\frac{x}{2}} = 2^s,$ $5^{\frac{z}{2}}-3^{\frac{x}{2}} = 2^t,$ $s+t = 2y,$ $s > t$ を満たす正の整数 $s,$ $t$ が存在することを示し, $t$ の値を求めよ.
- (4)
- $x = y = z = 2$ であることを示せ.
解答例
- (1)
- $3^x = 5^z-4^y$ かつ $3 \equiv -1,$ $5 \equiv 1 \pmod 4$ であるから, \[ (-1)^x \equiv 1^z-0^y = 1 \pmod 4\] が成り立つ. よって, $x$ は偶数である.
- (2)
- $5^z = 3^x+4^y$ かつ $5 \equiv -1,$ $4 \equiv 1 \pmod 3$ であるから, \[ (-1)^z \equiv 0^x+1^y = 1 \pmod 3\] が成り立つ. よって, $z$ は偶数である.
- (3)
- $5^x-3^x = 4^y,$ (1), (2) により, \[ (5^{\frac{z}{2}}+3^{\frac{x}{2}})(5^{\frac{z}{2}}-3^{\frac{x}{2}}) = 2^{2y}\] が成り立つ. よって, \[ 5^{\frac{z}{2}}+3^{\frac{x}{2}} = 2^s, \quad 5^{\frac{z}{2}}-3^{\frac{x}{2}} = 2^t, \quad s+t = 2y, \quad s > t\] を満たす正の整数 $s,$ $t$ が存在する. 第 $1$ 式から第 $2$ 式を引いて $2$ で割ると, \[ 3^{\frac{x}{2}} = \frac{2^s-2^t}{2} = 2^{t-1}(2^{s-t}-1)\] が得られる. ここで, $3^{\frac{x}{2}},$ $2^{t-1},$ $2^{s-t}-1$ は正の整数であるから, $t = 1$ である.
- (4)
- (3) により $s = 2y-1,$ $t = 1,$ したがって $2^{2y-2}-1 = 3^{\frac{x}{2}}$ であるから, \[ (2^{y-1}+1)(2^{y-1}-1) = 3^{\frac{x}{2}}\] が成り立つ. よって, \[ 2^{y-1}+1 = 3^u, \quad 2^{y-1}-1 = 3^v, \quad u+v = \frac{x}{2}, \quad u > v\] を満たす非負整数 $u,$ $v$ が存在する. 第 $1$ 式から第 $2$ 式を引くと, \[ 2 = 3^u-3^v = 3^v(3^{u-v}-1)\] が得られる. ここで, $3^v,$ $3^{u-v}-1$ は正の整数であるから, $(3^v,3^{u-v}-1) = (1,2)$ つまり $(u,v) = (1,0)$ である. このとき, $2^{y-1}-1 = 3^0 = 1$ から $y = 2$ であるので, $3^{\frac{x}{2}} = 2^{2\cdot 2-2}-1 = 3$ から $x = 2$ であり, さらに $5^z = 3^2+4^2 = 25$ から $z = 2$ が得られる. ゆえに, $x = y = z = 2$ である.
参考
本問は,「ピタゴラスの $3$ つ組」$(a,b,c)$ に対して
\[ a^x+b^y = c^z\]
の正の整数解は $(x,y,z) = (2,2,2)$ に限るという「イェスマノヴィッチ予想」 (Jesmanowicz conjecture) の $(a,b,c) = (3,4,5)$ の場合であり, 一般の場合は未解決である ($2024$ 年 $7$ 月現在).
次の場合などにこの予想が正しいことが確認されている.
- $(a,b,c) = (3,4,5)$ の場合 (Sierpinski, $1956$ 年).
- $(a,b,c) = (5,12,13),$ $(7,24,25),$ $(9,40,41),$ $(11,60,61)$ の場合 (Jesmanowicz, $1956$ 年).
- $(a,b,c) = (2k+1,2k(k+1),2k(k+1)+1)$ ($k$: 正の整数) の場合 (Demjanenko, $1965$ 年).
- $(a,b,c) = (4k^2-1,4k,4k^2+1)$ ($k$: 正の整数) の場合 (Grytczuk, Grelak, $1984$ 年).
- $(a,b,c) = (4k^2-p^2,4kp,4k^2+p^2)$ ($k$: 正の奇数, $p$: 素数, $p \equiv 3 \pmod 4$) かつ $y \neq 1$ の場合 (Takakuwa, Asaeda, $1993$ 年).
- $(a,b,c) = (4k^2-p^2,4kp,4k^2+p^2)$ ($k$: 正の奇数, $p$: 素数, $p \equiv 5 \pmod 8$) かつ $y$ が偶数の場合 (Takakuwa, $1993$ 年).
- $a,$ $b,$ $c$ が互いに素, $ab$ の素因数分解における $2$ の指数が $2,$ $c$ が奇素数の累乗の場合 (Le, $1995$ 年).
- $(a,b,c) = (m^2-n^2,2mn,m^2+n^2)$ ($m,$ $n$: 互いに素で偶奇の異なる正の整数, $m > n,$ $m$ の素因数分解における $2$ の指数が $1,$ $n \equiv 3 \pmod 4,$ $m \geqq 81n$) の場合 (Le, $1996$ 年).
問題《指数関数を含む方程式の整数解》
- (1)
- 関数 $f(x) = \dfrac{2^x}{x^2}$ について, $x \geqq 3$ のとき $f(x) < f(x+1)$ が成り立つことを示せ.
- (2)
- $2^x = x^2$ の整数解をすべて求めよ.
解答例
- (1)
- $x \neq 0$ のとき, $2^x > 0,$ $x^2 > 0$ から, $f(x) > 0$ であることに注意する. $x \geqq 3$ であるとする. このとき, $\dfrac{1}{x} \leqq \dfrac{1}{3}$ つまり $1+\dfrac{1}{x} \leqq \dfrac{4}{3}$ から, \[\left( 1+\frac{1}{x}\right) ^2 \leqq \frac{16}{9}\] が成り立つ. よって, \[\frac{f(x)}{f(x+1)} = \frac{2^x}{x^2}\cdot\frac{(x+1)^2}{2^{x+1}} = \frac{1}{2}\left( 1+\frac{1}{x}\right) ^2 \leqq \frac{1}{2}\cdot\frac{16}{9} < 1\] から, $f(x) < f(x+1)$ が成り立つ.
- (2)
- $x$ が負の整数のとき, $2^x < 1 \leqq x^2$ から, $2^x \neq x^2$ である.
- $x = 0$ のとき, $2^0 = 1 \neq 0 = 0^2$ から, $2^x \neq x^2$ である.
参考
$2^x = x^2$ の実数解は $3$ 個で, そのうちの $2$ 個が整数解 $x = 2,$ $4$ である (こちらを参照).
