累乗和の公式
累乗和の公式
定理《累乗和の公式》
すべての正の整数 $n$ に対して,
\[\begin{aligned}
\sum_{k = 1}^nk &= \frac{1}{2}n(n+1) \quad \cdots [1], \\
\sum_{k = 1}^nk^2 &= \frac{1}{6}n(n+1)(2n+1) \quad \cdots [2], \\
\sum_{k = 1}^nk^3 &= \frac{1}{4}n^2(n+1)^2 \quad \cdots [3]
\end{aligned}\]
が成り立つ.
証明 1
\[ 2x = (x+1)^2-x^2-1\]
に $x = 1,$ $\cdots,$ $n$ を代入して辺々を加えると
\[\begin{aligned}
2\sum_{k = 1}^nk &= (n+1)^2-1^2-n \\
&= (n+1)^2-(n+1) \\
&= n(n+1)
\end{aligned}\]
となるから, $[1]$ が成り立つ.
\[ 3x^2 = (x+1)^3-x^3-1-3x\]
に $x = 1,$ $\cdots,$ $n$ を代入して辺々を加えると
\[\begin{aligned}
3\sum_{k = 1}^nk^2 &= (n+1)^3-1^3-n-3\sum_{k = 1}^nk \\
&= (n+1)^3-(n+1)-3\cdot\frac{1}{2}n(n+1) \\
&= \frac{1}{2}(n+1)\{ 2(n+1)^2-2-3n\} \\
&= \frac{1}{2}(n+1)(2n^2+n) \\
&= \frac{1}{2}n(n+1)(2n+1)
\end{aligned}\]
となるから, $[2]$ が成り立つ.
\[ 4x^3 = (x+1)^4-x^4-1-4x-6x^2\]
に $x = 1,$ $\cdots,$ $n$ を代入して辺々を加えると
\[\begin{aligned}
4\sum_{k = 1}^nk^3 &= (n+1)^4-1^4-n-4\sum_{k = 1}^nk-6\sum_{k = 1}^nk^2 \\
&= (n+1)^4-(n+1) \\
&\qquad -4\cdot\frac{1}{2}n(n+1)-6\cdot\frac{1}{6}n(n+1)(2n+1) \\
&= (n+1)^4-(n+1)\\
&\qquad -2n(n+1)-n(n+1)(2n+1) \\
&= (n+1)\{ (n+1)^3-1-2n-n(2n+1)\} \\
&= (n+1)(n^3+n^2) \\
&= n^2(n+1)^2
\end{aligned}\]
となるから, $[3]$ が成り立つ.
証明 2
$\displaystyle\sum_{k = 1}^nk$ は, 初項 $1,$ 公差 $1,$ 項数 $n$ の等差数列の和であるから,
\[\displaystyle\sum_{k = 1}^nk = \frac{n}{2}\{ 2\cdot 1+1\cdot (n-1)\} = \frac{1}{2}n(n+1)\]
である.
また, $c_n = (n-1)n(n+1)$ とおくと,
\[ c_{n+1}-c_n = n(n+1)\{ (n+2)-(n-1)\} = 3n(n+1)\]
となるから,
\[\begin{aligned}
\sum_{k = 1}^nk(k+1) &= \frac{1}{3}\sum_{k = 1}^n(c_{k+1}-c_k) \\
\sum_{k = 1}^nk^2+\sum_{k = 1}^nk &= \frac{1}{3}n(n+1)(n+2)
\end{aligned}\]
であり,
\[\begin{aligned}
\sum_{k = 1}^nk^2 &= \frac{1}{3}n(n+1)(n+2)-\sum_{k = 1}^nk \\\
&= \frac{1}{3}n(n+1)(n+2)-\frac{1}{2}n(n+1) \\
&= \frac{1}{6}n(n+1)\{ 2(n+2)-3\} \\
&= \frac{1}{6}n(n+1)(2n+1)
\end{aligned}\]
が成り立つ.
同様に,
\[\begin{aligned}
\sum_{k = 1}^nk(k+1)(k+2) = \frac{1}{4}n(n+1)(n+2)(n+3)
\end{aligned}\]
であるから,
\[\begin{aligned}
\sum_{k = 1}^nk^3 &= \frac{1}{4}n(n+1)(n+2)-3\sum_{k = 1}^nk^2-2\sum_{k = 1}^nk \\
&= \frac{1}{4}n(n+1)(n+2)(n+3) \\
&\qquad -3\cdot\frac{1}{6}n(n+1)(2n+1)-2\cdot\frac{1}{2}n(n+1) \\
&= \frac{1}{4}n(n+1)\{ (n+2)(n+3)-2(2n+1)-4\} \\
&= \frac{1}{4}n(n+1)(n^2+n) \\
&= \frac{1}{4}n^2(n+1)^2
\end{aligned}\]
が成り立つ.
証明 3:「ベルヌーイ多項式」を利用
\[\begin{aligned}
&\int_x^{x+1}\left( t-\frac{1}{2}\right) dt = \left[\frac{t^2}{2}-\frac{t}{2}\right] _x^{x+1} = \frac{1}{2}[t(t-1)]_x^{x+1} \\
&= \frac{1}{2}\{ (x+1)x-x(x-1)\} = \frac{1}{2}\cdot 2x = x
\end{aligned}\]
であるから,
\[\begin{aligned}
\sum_{k = 1}^nk &= \sum_{k = 1}^n\int_k^{k+1}\left( t-\frac{1}{2}\right) dt = \int_1^{n+1}\left( t-\frac{1}{2}\right) dt \\
&= \frac{1}{2}[t(t-1)]_1^{n+1} = \frac{1}{2}n(n+1) \quad \cdots [1]
\end{aligned}\]
が成り立つ.
$[2]$ は, \[\int_x^{x+1}\left( t^2-t+\frac{1}{6}\right) dt = x^2\] を利用して, $[1]$ と同様に証明できる (こちらを参照).
また, \[\int_x^{x+1}\left( t^3-\frac{3}{2}t^2+\frac{1}{2}t\right) dt = x^3\] (計算は省略) を利用すると, \[\begin{aligned} \sum_{k = 1}^nk^3 &= \sum_{k = 1}^n\int_k^{k+1}\left( t^3-\frac{3}{2}t^2+\frac{1}{2}t\right) dt \\ &= \int_1^{n+1}\left( t^3-\frac{3}{2}t^2+\frac{1}{2}t\right) dt \\ &= \left[\frac{t^4}{4}-\frac{t^3}{2}+\frac{t^2}{4}\right] _1^{n+1} \\ &= \frac{1}{4}[t(t-1)(t^2-t-1)]_1^{n+1} \\ &= \frac{1}{4}(n+1)n\{ (n+1)^2-(n+1)-1\} \\ &= \frac{1}{4}n^2(n+1)^2 \quad \cdots [3] \end{aligned}\] が得られる.
$[2]$ は, \[\int_x^{x+1}\left( t^2-t+\frac{1}{6}\right) dt = x^2\] を利用して, $[1]$ と同様に証明できる (こちらを参照).
また, \[\int_x^{x+1}\left( t^3-\frac{3}{2}t^2+\frac{1}{2}t\right) dt = x^3\] (計算は省略) を利用すると, \[\begin{aligned} \sum_{k = 1}^nk^3 &= \sum_{k = 1}^n\int_k^{k+1}\left( t^3-\frac{3}{2}t^2+\frac{1}{2}t\right) dt \\ &= \int_1^{n+1}\left( t^3-\frac{3}{2}t^2+\frac{1}{2}t\right) dt \\ &= \left[\frac{t^4}{4}-\frac{t^3}{2}+\frac{t^2}{4}\right] _1^{n+1} \\ &= \frac{1}{4}[t(t-1)(t^2-t-1)]_1^{n+1} \\ &= \frac{1}{4}(n+1)n\{ (n+1)^2-(n+1)-1\} \\ &= \frac{1}{4}n^2(n+1)^2 \quad \cdots [3] \end{aligned}\] が得られる.
問題《平方三角数とペル方程式》
- (1)
- 図のように, $l$ 行 $l$ 列の正方形の形に並べられていた石を崩した後, $1$ 段目に $1$ 個, $\cdots,$ $k$ 段目に $k$ 個, $\cdots$ と $m$ 段目まで並べていくと, 正三角形の形に石を余すことなく並べられたとする.
このとき, $(x,y) = (2m+1,2l)$ は $x^2-2y^2 = 1$ の解であることを示せ.
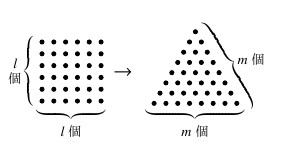
- (2)
- $(x,y)$ を $x^2-2y^2 = 1$ の正の整数解とする.
このとき, $x$ は $3$ 以上の奇数であり, $y$ は偶数であることを示せ.
さらに, $l = \dfrac{y}{2},$ $m = \dfrac{x-1}{2}$ とおくと, 上記のように, $l$ 行 $l$ 列の正方形の形に並べられた石は $m$ 段の正三角形の形にも並べられることを示せ.
(参考: $1994$ 津田塾大)
解答例
- (1)
- 石の個数に関する条件から \[ l^2 = \displaystyle\sum_{k = 1}^mk = \frac{1}{2}m(m+1)\] であるので, \[\begin{aligned} &(2m+1)^2-2(2l)^2 = (2m+1)^2-8l^2 \\ &= (2m+1)^2-8\cdot\frac{1}{2}m(m+1) \\ &= (4m^2+4m+1)-(4m^2+4m) = 1 \end{aligned}\] が成り立つ. よって, $(x,y) = (2m+1,2l)$ は $x^2-2y^2 = 1$ の解である.
- (2)
- $x^2 = 2y^2+1$ は奇数で, $x$ は奇数であるから, $x = 2m+1$ ($m$: 非負整数) とおける. $x = 1$ とすると, $-2y^2 = 0$ となり, $y = 0$ となってしまうから, $x \geqq 3$ である. また, $y = 2k+1$ ($k$: 非負整数) とすると, $x^2-2y^2 = 4(m^2+m-2k^2-2k)-1$ を $4$ で割った余りが $3 \neq 1$ となってしまうから, $y$ は偶数である. そこで, $y = 2l$ ($l$: 正の整数) とおくと, $(2m+1)^2-8l^2 = 1$ から \[\begin{aligned} l^2 &= \frac{(2m+1)^2-1}{8} = \frac{4m^2+4m}{8} \\ &= \frac{1}{2}m(m+1) = \sum_{k = 1}^mk \end{aligned}\] となるので, $l$ 行 $l$ 列の正方形の形に並べられた石は $m$ 段の正三角形の形にも並べられる.
参考
- 正三角形の形に点を並べたときの点の総数を「三角数」と呼び, 平方数でも「三角数」でもある整数を「平方三角数」と呼ぶ.
- 平方数でないある正の整数 $d$ に対して, $x^2-dy^2 = 1$ または $x^2-dy^2 = -1$ の形の方程式を「ペル方程式」と呼ぶ. 本問で示したように,「平方三角数」と「ペル方程式」$x^2-2y^2 = 1$ の正の整数解 $(x,y)$ は $1$ 対 $1$ に対応している. このことと $x^2-2y^2 = 1$ の一般解 (こちらを参照) を合わせると, 小さい方から $n$ 番目の「平方三角数」 $l^2$ は, $y = 2l$ から, $l^2 = \dfrac{y^2}{4} = \dfrac{\{ (3+2\sqrt 2)^n-(3-2\sqrt 2)^n\} ^2}{32}$ と表せることがわかる (L・オイラー, $1778$ 年). 小さい順に「平方三角数」を列記すると, $1,$ $36,$ $1225,$ $41616,$ $1413721,$ $\cdots$ となる.
問題《多角錐数の一般項》
$p$ を $3$ 以上の整数とする.
\[ a_n = \frac{(p-2)n^2-(p-4)n}{2}\]
で定まる数列 $\{ a_n\}$ の初項から第 $n$ 項までの和 $S_n$ を求めよ.
解答例
求める和は,
\[\begin{aligned}
S_n &= \sum_{k = 1}^na_k \\
&= \sum_{k = 1}^n\frac{(p-2)k^2-(p-4)k}{2} \\
&= \frac{p-2}{2}\sum_{k = 1}^nk^2-\frac{p-4}{2}\sum_{k = 1}^nk \\
&= \frac{p-2}{2}\cdot\frac{n(n+1)(2n+1)}{6}-\frac{p-4}{2}\cdot\frac{n(n+1)}{2} \\
&= \frac{n(n+1)}{12}\{ (p-2)(2n+1)-3(p-4)\} \\
&= \frac{n(n+1)}{12}\{ 2(p-2)n-2(p-5)\} \\
&= \frac{n(n+1)\{ (p-2)n-(p-5)\}}{6}
\end{aligned}\]
である.
参考
- $S_n$ $(n \geqq 1)$ は,「$p$ 角数」$a_n$ $(n \geqq 1)$ (こちらを参照) の $3$ 次元版であり, 「$p$ 角錐数」と呼ばれる.
- $n$ 番目の正の整数は $n,$ $n$ 番目の「三角数」は $\dfrac{n(n+1)}{2},$ $n$ 番目の「三角錐数」は $\dfrac{n(n+1)(n+2)}{6}$ である. $1$ 番目から $n$ 番目までの「三角錐数」の和は, $\dfrac{n(n+1)(n+2)(n+3)}{24}$ であり,「五胞体数」と呼ばれる.
問題《数列の積の和の最大値》
$\{ a_1,\cdots,a_n\} = \{ 1,\cdots,n\}$ とする.
数列 $\{ ka_k\}$ の和 $S = \displaystyle\sum_{k = 1}^nka_k$ の最大値を求めよ.
解答例
$(a_k-k)^2 = a_k{}^2-2ka_k+k^2$ であるから,
\[ ka_k = \frac{1}{2}\{ a_k{}^2+k^2-(a_k-k)^2\}\]
が成り立つ.
$k = 1,$ $\cdots,$ $n$ を代入して辺々を加えると
\[\begin{aligned}
S &= \sum_{k = 1}^nka_k \\
&= \frac{1}{2}\left\{\sum_{k = 1}^na_k{}^2+\sum_{k = 1}^nk^2-\sum_{k = 1}^n(a_k-k)^2\right\} \\
&= \sum_{k = 1}^nk^2-\frac{1}{2}\sum_{k = 1}^n(a_k-k)^2 \\
&= \frac{1}{6}n(n+1)(2n+1)-\frac{1}{2}\sum_{k = 1}^n(a_k-k)^2
\end{aligned}\]
が得られるから, $S$ は $a_k = k$ $(1 \leqq k \leqq n)$ のとき最大値
\[\frac{1}{6}n(n+1)(2n+1)\]
をとる.
参考
一般に, $x_1 \geqq \cdots \geqq x_n,$ $y_1 \geqq \cdots \geqq y_n,$ $\{\sigma (1),\cdots,\sigma (n)\} = \{ 1,\cdots,n\}$ のとき,「並べ替え不等式」
\[\sum_{k = 1}^nx_ky_k \geqq \sum_{k = 1}^nx_ky_{\sigma (k)} \geqq \sum_{k = 1}^nx_ky_{n-k+1}\]
が成り立つ.
問題《$4$ 乗数の和の公式》
すべての正の整数 $n$ に対して
\[\sum_{k = 1}^nk^4 = \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1)\]
が成り立つことを示せ.
解答例
\[ 5x^4 = (x+1)^5-x^5-1-5x-10x^2-10x^3\]
に $x = 1,$ $\cdots,$ $n$ を代入して辺々を加えると
\[\begin{aligned}
5\sum_{k = 1}^nk^4 &= (n+1)^5-1^5-n-5\!\sum_{k = 1}^n\!k-10\!\sum_{k = 1}^n\!k^2-10\!\sum_{k = 1}^n\!k^3 \\
&= (n+1)^5-(n+1)-5\cdot\frac{1}{2}n(n+1) \\
&\qquad -10\cdot\frac{1}{6}n(n+1)(2n+1)-10\cdot\frac{1}{4}n^2(n+1)^2 \\
&= \frac{1}{6}(n+1)\{ 6(n+1)^4-6-15n \\
&\qquad -10n(2n+1)-15n^2(n+1)\} \\
&= \frac{1}{6}(n+1)(6n^4+9n^3+n^2-n) \\
&= \frac{1}{6}n(n+1)(6n^3+9n^2+n-1) \\
&= \frac{1}{6}n(n+1)\left( n+\frac{1}{2}\right) (6n^2+6n-2) \\
&= \frac{1}{6}n(n+1)(2n+1)(3n^2+3n-1)
\end{aligned}\]
となるから, 両辺を $5$ で割ると
\[\sum_{k = 1}^nk^4 = \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1)\]
が得られる.
参考
\[\int_x^{x+1}\left( t^4-2t^3+t^2-\frac{1}{30}\right) dt = x^4\]
(計算は省略) を利用すると,
\[\begin{aligned}
\sum_{k = 1}^nk^4 &= \sum_{k = 1}^n\int_k^{k+1}\left( t^4-2t^3+t^2-\frac{1}{30}\right) dt \\
&= \int_1^{n+1}\left( t^4-2t^3+t^2-\frac{1}{30}\right) dt \\
&= \left[\frac{t^5}{5}-\frac{t^4}{2}+\frac{t^3}{3}-\frac{t}{30}\right] _1^{n+1} \\
&= \frac{1}{30}[t(t-1)(2t-1)(3t^2-3t-1)]_1^{n+1} \\
&= \frac{1}{30}(n+1)n(2n+1)\{ 3(n+1)^2-3(n+1)-1\} \\
&= \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1)
\end{aligned}\]
が得られる.
問題《格子に含まれる長方形の面積の平均値》
$n$ を $1$ より大きい整数とする.
$1$ 辺の長さが $n$ の正方形において, 各辺を $n$ 等分する点をとり, 向かい合う $2$ 辺の等分点を通って辺に平行な直線 $2(n-1)$ 本を引く.
もとの正方形の辺やこれらの直線が囲む長方形について,
- (1)
- 個数を求めよ.
- (2)
- 面積の総和 (のべ面積) を求めよ.
- (3)
- 面積の平均値を求めよ.
(オリジナル)
解答例
隣り合う $2$ 辺の長さが $k,$ $l$ $(1 \leqq k \leqq n,$ $1 \leqq l \leqq n)$ である長方形は $(n-k+1)(n-l+1)$ 個ある.
- (1)
- 求める個数は, \[\begin{aligned} &\sum_{k = 1}^n\sum_{l = 1}^n(n-k+1)(n-l+1) \\ &= \sum_{k = 1}^n\sum_{l = 1}^nkl = \left(\sum_{k = 1}^nk\right)\left(\sum_{l = 1}^nl\right) = \left(\sum_{k = 1}^nk\right) ^2 \\ &= \left\{\frac{1}{2}n(n+1)\right\} ^2 \quad \cdots [1] \end{aligned}\] である.
- (2)
- 求める面積は, \[\begin{aligned} &\sum_{k = 1}^n\sum_{l = 1}^n(n-k+1)(n-l+1)kl \\ &= \left\{\sum_{k = 1}^n(n-k+1)k\right\}\left\{\sum_{l = 1}^n(n-l+1)l\right\} \\ &= \left\{\sum_{k = 1}^n(n-k+1)k\right\} ^2 \\ &= \left\{ \frac{1}{6}n(n+1)(n+2)\right\} ^2 \quad \cdots [2] \end{aligned}\] である. ここで, \[\begin{aligned} &\sum_{k = 1}^n(n-k+1)k = \sum_{k = 1}^n\{ (n+1)k-k^2\} \\ &= (n+1)\sum_{k = 1}^nk-\sum_{k = 1}^nk^2 \\ &= (n+1)\frac{1}{2}n(n+1)-\frac{1}{6}n(n+1)(2n+1) \\ &= \frac{1}{6}n(n+1)\{ 3(n+1)-(2n+1)\} \\ &= \frac{1}{6}n(n+1)(n+2) \end{aligned}\] であることを使った.
- (3)
- 求める面積の平均値は, $[2]\div [1]$ から, \[\left\{ \frac{1}{6}n(n+1)(n+2)\right\} ^2\div\left\{\frac{1}{2}n(n+1)\right\} ^2 = \frac{(n+2)^2}{9}\] である.
参考
全体の面積に対する小長方形の面積の比の極限については, こちらを参照.
問題《格子に含まれる正方形の面積の平均値》
$n$ を $1$ より大きい整数とする.
$1$ 辺の長さが $n$ の正方形において, 各辺を $n$ 等分する点をとり, 向かい合う $2$ 辺の等分点を通って辺に平行な直線 $2(n-1)$ 本を引く.
もとの正方形の辺やこれらの直線が囲む正方形について,
- (1)
- 個数を求めよ.
- (2)
- 面積の総和 (のべ面積) を求めよ. ただし, \[\sum_{k = 1}^nk^4 = \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1)\] が成り立つこと (こちらを参照) は, 証明なしに使ってよい.
- (3)
- 面積の平均値を求めよ.
(オリジナル)
解答例
$1$ 辺の長さが $k$ $(1 \leqq k \leqq n)$ である正方形は $(n-k+1)^2$ 個ある.
- (1)
- 求める個数は, \[\sum_{k = 1}^n(n-k+1)^2 = \sum_{k = 1}^nk^2 = \frac{1}{6}n(n+1)(2n+1) \quad \cdots [1]\] である.
- (2)
- 求める面積は, \[\begin{aligned} &\sum_{k = 1}^n(n-k+1)^2k^2 \\ &= \sum_{k = 1}^n\{ (n+1)^2-2(n+1)k+k^2\} k^2 \\ &= \sum_{k = 1}^n\{ (n+1)^2k^2-2(n+1)k^3+k^4\} \\ &= (n+1)^2\sum_{k = 1}^nk^2-2(n+1)\sum_{k = 1}^nk^3+\sum_{k = 1}^nk^4 \\ &= (n+1)^2\cdot\frac{1}{6}n(n+1)(2n+1) \\ &\qquad -2(n+1)\cdot\frac{1}{4}n^2(n+1)^2 \\ &\qquad +\frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1) \\ &= \frac{1}{30}n(n+1)\{ 5(n+1)^2(2n+1) \\ &\qquad -15n(n+1)^2+(2n+1)(3n^2+3n-1)\} \\ &= \frac{1}{30}n(n+1)(n^3+4n^2+6n+4) \\ &= \frac{1}{30}n(n+1)(n+2)(n^2+2n+2) \quad \cdots [2] \end{aligned}\] である.
- (3)
- 求める面積の平均値は, $[2]\div [1]$ から, \[\begin{aligned} &\frac{1}{30}n(n+1)(n+2)(n^2+2n+2)\div\frac{1}{6}n(n+1)(2n+1) \\ &= \frac{(n+2)(n^2+2n+2)}{5(2n+1)} \end{aligned}\] である.
参考
全体の面積に対する小正方形の面積の比の極限については, こちらを参照.
問題《累乗数の和を表す多項式の存在》
すべての正の整数 $m$ に対して
\[\sum_{k = 1}^nk^m = S_m(n) \quad (n \geqq 1)\]
を満たす $m+1$ 次多項式 $S_m(x)$ が存在することを示せ.
(参考: $2023$ 大阪公立大)
解答例
$m$ に関する数学的帰納法で示す.
- (i)
- $m = 1$ のとき. \[ 2x = (x+1)^2-x^2-1\] に $x = 1,$ $\cdots,$ $n$ を代入して辺々を加えると \[\begin{aligned} 2\sum_{k = 1}^nk &= (n+1)^2-1^2-n \\ &= (n+1)^2-(n+1) \\ &= n(n+1) \end{aligned}\] となるから, \[ S_1(x) = \frac{1}{2}x(x+1)\] は \[\sum_{k = 1}^nk = S_1(n) \quad (n \geqq 1)\] を満たす.
- (ii)
- $m > 1$ として $S_1(x),$ $\cdots,$ $S_{m-1}(x)$ の存在を仮定する. 二項定理により, \[\begin{aligned} (x+1)^{m+1} &= 1+\sum_{j = 1}^{m-1}{}_{m+1}\mathrm C_jx^j+(m+1)x^m+x^{m+1} \\ (m+1)x^m &= (x+1)^{m+1}-x^{m+1}-1-\sum_{j = 1}^{m-1}{}_{m+1}\mathrm C_jx^j \end{aligned}\] が成り立つ. $x = 1,$ $\cdots,$ $n$ を代入して辺々を加えると \[\begin{aligned} &(m+1)\sum_{k = 1}^nk^m \\ &= (n+1)^{m+1}-1^{m+1}-n-\sum_{k = 1}^n\sum_{j = 1}^{m-1}{}_{m+1}\mathrm C_jk^j \\ &= (n+1)^{m+1}-(n+1)-\sum_{j = 1}^{m-1}{}_{m+1}\mathrm C_j\sum_{k = 1}^nk^j \\ &= (n+1)^{m+1}-(n+1)-\sum_{j = 1}^{m-1}{}_{m+1}\mathrm C_jS_j(n) \\ \end{aligned}\] となるから, \[ S_m(x) = \frac{1}{m+1}\left\{ (x+1)^{m+1}-(x+1)-\sum_{j = 1}^{m-1}{}_{m+1}\mathrm C_jS_j(x)\right\}\] とおくと, 右辺の $(x+1)^{m+1}$ は $m+1$ 次でそれ以外の項は $m$ 次以下であるから $S_m(x)$ は $m+1$ 次になり, \[\sum_{k = 1}^nk^m = S_m(n) \quad (n \geqq 1)\] となる.
参考
一般に,「ファウルハーバーの公式」(Faulhaber's formula)
\[\sum_{k = 1}^nk^m = \frac{1}{m+1}\sum_{k = 0}^m(-1)^k{}_{m+1}\mathrm C_kB_kn^{m-k+1}\]
が成り立つ.
ここで, $B_0,$ $\cdots,$ $B_m$ は「ベルヌーイ数」(Bernoulli number) と呼ばれる有理数で, $B_0 = 1$ と
\[\sum_{k = 0}^m{}_{m+1}\mathrm C_kB_k = 0\]
という関係式で定まる (こちらも参照).
問題《累乗数の和を表す多項式の性質》
$m$ を正の整数とする.
$S_m(0) = 0$ と各正の整数 $n$ に対して $\displaystyle\sum_{k = 1}^nk^m = S_m(n)$ を満たす $m+1$ 次多項式 $S_m(x)$ (こちらを参照) について, 次のことを示せ.
- (1)
- 多項式 $f(x)$ に対して,
- (i)
- $f(x) = S_m(x)$
- (ii)
- $f(0) = 0,$ $f(n)-f(n-1) = n^m$ ($n$: 正の整数)
- (iii)
- $f(0) = 0,$ $f(x)-f(x-1) = x^m$
- (2)
- $S_m(x) = (-1)^{m-1}S_m(-x-1)$ が成り立つ.
- (3)
- $y = S_m(x)$ のグラフは, $m$ が偶数のとき点 $\left( -\dfrac{1}{2},0\right)$ に関して対称, $m$ が奇数のとき直線 $x = -\dfrac{1}{2}$ に関して対称である.
- (4)
- $S_m(x)-\dfrac{1}{2}x^m$ は, $m$ が偶数のとき奇関数, $m$ が奇数のとき偶関数である.
- (5)
- $m \geqq 2$ とする. $S_m(x)$ は, $m$ が偶数のとき $S_2(x)$ で, $m$ が奇数のとき $S_1(x)^2$ で割り切れる.
解答例
- (1)
- (i) $\Longrightarrow$ (ii) は明らかである.
(ii) $\Longrightarrow$ (i) を示すため, $f(x)$ が (ii) を満たすとする. \[ f(k)-f(k-1) = k^m \quad (1 \leqq k \leqq n)\] の辺々を加えると, \[ f(n) = f(n)-f(0) = \sum_{k = 1}^nk^m = S_m(n)\] が得られる. 方程式 $f(x)-S_m(x) = 0$ はすべての正の整数を解にもつから, 多項式の差 $f(x)-S_m(x)$ は $0$ にならざるを得ない ($0$ でないとすると, $f(x)-S_m(x) = 0$ の解の個数が有限になってしまう). よって, $f(x) = S_m(x)$ が成り立つ.
(ii) $\Longrightarrow$ (iii) を示すため, $f(x)$ が (ii) を満たすとする. 方程式 $f(x)-f(x-1)-x^m = 0$ はすべての正の整数を解にもつから, 多項式の差 $f(x)-f(x-1)-x^m$ は $0$ にならざるを得ない (理由は上記と同じ). よって, $f(x)-f(x-1) = x^m$ が成り立つ.
(iii) $\Longrightarrow$ (ii) は明らかである.
以上から, (i)~(iii) は同値である. - (2)
- $f(x) = (-1)^{m-1}S_m(-x-1)$ とおく. \[ S_m(x)-S_m(x-1) = x^m\] に $0$ を代入すると $S_m(0) = 0,$ $S_m(0)-S_m(-1) = 0$ から $S_m(-1) = 0$ が得られるので, \[ f(0) = (-1)^{m-1}S_m(-1) = 0\] が成り立つ. \[\begin{aligned} &f(x)-f(x-1) \\ &= (-1)^{m-1}S_m(-x-1)-(-1)^{m-1}S_m(-x) \\ &= -(-1)^{m-1}\{ S_m(-x)-S_m(-x-1)\} \\ &= (-1)^m(-x)^m = x^m \end{aligned}\] も成り立つから, (1) により, $f(x) = S_m(x)$ つまり \[ S_m(x) = (-1)^{m-1}S_m(-x-1) \quad \cdots [1]\] が成り立つ.
- (3)
- 実数 $x,$ $x',$ $a$ に対して, $\dfrac{x+x'}{2} = a$ $\iff$ $x' = -x+2a$ から,
- $y = f(x)$ が点 $(a,0)$ に関して対称 \[\iff f(-x+2a) = -f(x)\]
- $y = f(x)$ が直線 $x = a$ に関して対称 \[\iff f(-x+2a) = f(x)\]
- (4)
- $S_m(-x)-S_m(-x-1) = (-x)^m$ と $[2]$ から \[\begin{aligned} S_m(-x)-\frac{1}{2}(-x)^m &= S_m(-x-1)+\frac{1}{2}(-x)^m \\ &= (-1)^{m-1}S_m(x)-(-1)^{m-1}\frac{1}{2}x^m \\ &= (-1)^{m-1}\left\{ S_m(x)-\frac{1}{2}x^m\right\} \end{aligned}\] が成り立つので, $S_m(x)-\dfrac{1}{2}x^m$ は, $m$ が偶数のとき奇関数, $m$ が奇数のとき偶関数である.
- (5)
- $m$ が偶数のとき. $S_m(0) = 0$ であり, $y = S_m(x)$ のグラフは点 $\left( -\dfrac{1}{2},0\right)$ に関して対称であるから, $S_m(-1) = 0,$ $S_m\left( -\dfrac{1}{2}\right) = 0$ も成り立つ. ゆえに, 因数定理により, $S_m(x)$ は $x,$ $x+1,$ $x+\dfrac{1}{2}$ で割り切れるから, $\dfrac{1}{6}x(x+1)(2x+1) = S_2(x)$ で割り切れる.
- $m$ が $3$ 以上の奇数のとき. $S_m(0) = 0$ であり, $S_m(x)-\dfrac{1}{2}x^m$ は偶関数であるから, $S_m(x)$ の定数項と $1$ 次の項は $0$ であり, $S_m(x)$ は $x^2$ で割り切れる. $y = S_m(x)$ のグラフは原点で $x$ 軸に接し, 直線 $x = -\dfrac{1}{2}$ に関して対称であるから, 点 $(-1,0)$ でも $x$ 軸に接し, $S_m(x)$ は $(x+1)^2$ で割り切れる. ゆえに, $S_m(x)$ は $\dfrac{1}{4}x^2(x+1)^2 = S_1(x){}^2$ で割り切れる.
参考
\[\begin{aligned}
S_3(x) &= S_1(x)^2, \\
S_4(x) &= \dfrac{1}{5}S_2(x)(3x^2+3x-1), \\
S_5(x) &= \dfrac{1}{3}S_1(x)^2(2x^2+2x-1), \\
S_6(x) &= \dfrac{1}{7}S_2(x)(3x^4+6x^3-3x+1)
\end{aligned}\]
が成り立つ.
問題《平方根の整数部分の和》
実数 $x$ に対して, $x$ 以下の整数の最大値を $[x]$ で表す.
$a_n = [\sqrt n]$ で定まる数列 $\{ a_n\}$ の初項から第 $n$ 項までの和を $S_n$ とおく.
$k,$ $m$ を正の整数とする.
- (1)
- $a_n = k$ を満たす数列 $\{ a_n\}$ の項の個数を求めよ.
- (2)
- $S_{m^2}$ を $m$ の式で表せ.
解答例
- (1)
- \[\begin{aligned} a_n = k &\iff [\sqrt n] = k \\ &\iff k \leqq \sqrt n < k+1 \\ &\iff k^2 \leqq n < (k+1)^2 \end{aligned}\] が成り立つから, $a_n = k$ を満たす数列 $\{ a_n\}$ の項の個数は, \[ (k+1)^2-k^2 = 2k+1\] である.
- (2)
- $n = m^2$ は $a_n = m$ を満たす最小の番号であるので, (1) の結果から, \[\begin{aligned} S_{m^2} &= \sum_{k = 1}^{m-1}(2k+1)k+m \\ &= 2\sum_{k = 1}^{m-1}k^2+\sum_{k = 1}^{m-1}k+m \\ &= 2\cdot\frac{1}{6}(m-1)m(2m-1)+\frac{1}{2}(m-1)m+m \\ &= \frac{1}{6}m\{ 2(m-1)(2m-1)+3(m-1)+6\} \\ &= \frac{1}{6}m(4m^2-3m+5) \end{aligned}\] である.
問題《整数の組と整数の対応》
すべての正の整数の組 $(k,l)$ を, $k+l$ の値が小さい順に並べ, $k+l$ の値が等しい組については $k$ の値が大きい順に並ぶようにする.
このとき, 正の整数の組 $(k,l)$ は何番目に並べられるか.
解答例
正の整数の組 $(k,l)$ に対して, $n = k+l$ とおく.
すべての正の整数の組を上記のように並べ, $n$ の値ごとに群に分ける.
\[ (1,1) \mid (2,1),(1,2) \mid (3,1),(2,2),(1,3) \mid \cdots\]
このとき, $k+l = n$ を満たす整数の組が属するのは第 $n-1$ 群で, その群に属する整数の組は $n-1$ 個である.
よって, 第 $1$ 群から第 $n-1$ 群までに属する整数の組の個数は,
\[\sum_{m = 1}^{n-1}m = \frac{(n-1)n}{2}\]
である.
$(k,l)$ は第 $n-1$ 群の末尾から $k$ 番目の位置にあるので, $(k,l)$ が並ぶのは,
$\dfrac{(n-1)n}{2}-k+1 = \dfrac{(k+l-1)(k+l)}{2}-k+1$ (番目)
である.
参考
- 本問の結果から, 正の整数の組と正の整数は, \[ f(k,l) = \frac{(k+l-1)(k+l)}{2}-k+1\] という $2$ 変数関数によって, もれも重複もなく対応していることがわかる. このように, 集合 $X$ の要素 $x$ を集合 $Y$ のある要素 $f(x)$ にそれぞれ対応させる, もれも重複もない対応を, $X$ から $Y$ への「全単射」(bijection) と呼ぶ. $X$ から $Y$ への「全単射」が存在するとき, $X,$ $Y$ は「対等」(equivalent) であるという.
- 次のことがよく知られている.
ただし, 非負整数全体の集合を $\mathbb N,$ 整数全体の集合を $\mathbb Z,$ 正の整数全体の集合を $\mathbb Z_+,$ 偶数全体の集合を $2\mathbb Z$ で表す.
また, 有理数全体の集合を $\mathbb Q,$ 実数全体の集合を $\mathbb R$ で表す.
- 有限集合, $\mathbb Z_+$ は「対等」でない.
- $\mathbb N$ と $\mathbb Z_+$ の間には「全単射」$f(n) = n+1$ $(n \in \mathbb N)$ があるから, $\mathbb N,$ $\mathbb Z_+$ は「対等」である.
- $\mathbb Z$ と $2\mathbb Z$ の間には「全単射」$f(n) = 2n$ $(n \in \mathbb Z)$ があるから, $\mathbb Z,$ $2\mathbb Z$ は「対等」である.
- $\mathbb N,$ $\mathbb Z,$ $\mathbb Q$ は「対等」である.
- 「カントールの定理」: $\mathbb N,$ $\mathbb R$ は「対等」でない ($1874$ 年).
