数列の極限
数列の極限
数列の極限の厳密な定義は, 高校数学の範囲を超えるが, 参考のためにここで紹介しておく.
定義《数列の極限》
$\{ a_n\}$ を実数列, $\alpha$ を実数とする.
- (1)
- 任意の正の数 $\varepsilon$ に対して, ある正の整数 $n_0$ が存在して, \[ n \geqq n_0 \Longrightarrow |a_n-\alpha | < \varepsilon\] が成り立つとき, $\{ a_n\}$ は $\alpha$ に収束する (converge) といい, $\lim\limits_{n \to \infty}a_n = \alpha$ または $a_n \to \infty\ (n \to \infty )$ と表す. $\alpha$ を $\{ a_n\}$ の極限値 (limit) と呼ぶ.
- (2)
- $\{ a_n\}$ がどの実数にも収束しないとき, $\{ a_n\}$ は発散する (diverge) という.
- (i)
- 任意の実数 $G$ に対して, ある正の整数 $n_0$ が存在して, \[ n \geqq n_0 \Longrightarrow a_n > G\] が成り立つとき, $\{ a_n\}$ は $\infty$ に発散するといい, $\lim\limits_{n \to \infty}a_n = \infty$ または $a_n \to \infty\ (n \to \infty )$ と表す.
- (ii)
- 任意の実数 $G$ に対して, ある正の整数 $n_0$ が存在して, \[ n \geqq n_0 \Longrightarrow a_n < G\] が成り立つとき, $\{ a_n\}$ は $-\infty$ に発散するといい, $\lim\limits_{n \to \infty}a_n = -\infty$ または $a_n \to -\infty\ (n \to \infty )$ と表す.
- (iii)
- $\{ a_n\}$ が発散して, $\infty$ にも $-\infty$ にも発散しないとき, $\{ a_n\}$ は振動する (oscillate) という.
定理《等差数列・調和数列の極限》
\[\lim\limits_{n \to \infty}n = \infty, \quad \lim\limits_{n \to \infty}\frac{1}{n} = 0\]
が成り立つ.
定理《数列の極限と四則演算の交換可能性》
$c$ を実数とする.
数列 $\{ a_n\},$ $\{ b_n\}$ が収束するとき,
\[\begin{aligned}
\lim\limits_{n \to \infty}(a_n\pm b_n) &= \lim\limits_{n \to \infty}a_n\pm\lim\limits_{n \to \infty}b_n \quad \cdots [1] \\
\lim\limits_{n \to \infty}a_nb_n &= \left(\lim\limits_{n \to \infty}a_n\right)\left(\lim\limits_{n \to \infty}b_n\right) \quad \cdots [2] \\
\lim\limits_{n \to \infty}ca_n &= c\lim\limits_{n \to \infty}a_n \quad \cdots [2]' \\
\lim\limits_{n \to \infty}\frac{a_n}{b_n} &= \frac{\lim\limits_{n \to \infty}a_n}{\lim\limits_{n \to \infty}b_n} \quad \cdots [3] \\
\end{aligned}\]
が成り立つ.
ただし, $[3]$ では $b_n \neq 0,$ $\lim\limits_{n \to \infty}b_n \neq 0$ を仮定する.
定理《挟みうち・追い出しの原理》
- (A)
- 数列 $\{ a_n\},$ $\{ b_n\},$ $\{ c_n\},$ 実数 $L$ に対して, \[ a_n \leqq b_n \leqq c_n,\ \lim\limits_{n \to \infty}a_n = \lim\limits_{n \to \infty}c_n = L \Longrightarrow \lim\limits_{n \to \infty}b_n = L\] が成り立つ.
- (B)
- 数列 $\{ a_n\},$ $\{ b_n\}$ に対して, \[\begin{aligned} a_n \leqq b_n,\ \lim\limits_{n \to \infty}a_n = \infty &\Longrightarrow \lim\limits_{n \to \infty}b_n = \infty, \\ a_n \leqq b_n,\ \lim\limits_{n \to \infty}b_n = -\infty &\Longrightarrow \lim\limits_{n \to \infty}a_n = -\infty \end{aligned}\] が成り立つ.
問題《格子に含まれる長方形の面積の平均値の極限》
$n$ を $1$ より大きい整数とする.
$1$ 辺の長さが $1$ の正方形において, 各辺を $n$ 等分する点をとり, 向かい合う $2$ 辺の等分点を通って辺に平行な直線 $2(n-1)$ 本を引く.
このとき, もとの正方形の辺やこれらの直線が囲む長方形の面積の平均値 $a_n$ は
\[ a_n = \dfrac{(n+2)^2}{9n^2}\]
である (こちらを参照).
極限値 $\lim\limits_{n \to \infty}a_n$ を求めよ.
(オリジナル)
解答例
\[ a_n = \frac{(n+2)^2}{9n^2} = \frac{1}{9}\left( 1+\dfrac{2}{n}\right) ^2 \to \frac{1}{9} \quad (n \to \infty )\]
であるから, $\lim\limits_{n \to \infty}a_n = \dfrac{1}{9}$ である.
参考
本問の結果は高次元に一般化され,「$d$ 次元超立方体」における「標準大の超直方体」の「$d$ 次元体積」は $\dfrac{1}{3^d}$ である (こちらを参照; 廣津, $2021$ 年).
本問の答えの $9$ は $3^2$ からきている.
問題《格子に含まれる正方形の面積の平均値の極限》
$n$ を $1$ より大きい整数とする.
$1$ 辺の長さが $1$ の正方形において, 各辺を $n$ 等分する点をとり, 向かい合う $2$ 辺の等分点を通って辺に平行な直線 $2(n-1)$ 本を引く.
このとき, もとの正方形の辺やこれらの直線が囲む正方形の面積の平均値 $a_n$ は
\[ a_n = \dfrac{(n+2)(n^2+2n+2)}{5n^2(2n+1)}\]
である (こちらを参照).
極限値 $\lim\limits_{n \to \infty}a_n$ を求めよ.
(オリジナル)
解答例
\[\begin{aligned}
a_n &= \frac{(n+2)(n^2+2n+2)}{5n^2(2n+1)} = \frac{\left( 1+\dfrac{2}{n}\right)\left( 1+\dfrac{2}{n}+\dfrac{2}{n^2}\right)}{5\left( 2+\dfrac{1}{n}\right)} \\
&\to \frac{1}{10} \quad (n \to \infty )
\end{aligned}\]
であるから, $\lim\limits_{n \to \infty}a_n = \dfrac{1}{10}$ である.
参考
本問の結果は高次元に一般化され,「$d$ 次元超立方体」における「標準大の超立方体」の「$d$ 次元体積」は $\dfrac{1}{{}_{2d+1}\mathrm C_d}$ である (こちらを参照; 廣津, $2021$ 年).
本問の答えの $10$ は ${}_{2\cdot 2+1}\mathrm C_2$ からきている.
無限等比数列の極限
定理《無限等比数列の極限》
$r > -1$ のとき,
\[\lim\limits_{n \to \infty}r^n = \begin{cases}
\infty & (r > 1), \\
1 & (r = 1), \\
0 & (|r| < 1)
\end{cases}\]
が成り立つ.
$r \leqq -1$ のとき, $\{ r^n\}$ は振動する.
問題《フィボナッチ数列の隣接項の比の極限》
$F_1 = F_2 = 1,$ $F_{n+2} = F_n+F_{n+1}$ で定まる数列 $\{ F_n\}$ は「フィボナッチ数列」と呼ばれ, その一般項は
\[ F_n = \frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^n-\left(\frac{1-\sqrt 5}{2}\right) ^n\right\}\]
であることが知られている (証明はこちらを参照).
この数列について, 隣り合う項の比の極限 $\lim\limits_{n \to \infty}\dfrac{F_{n+1}}{F_n}$ を求めよ.
解答例
$\alpha = \dfrac{1+\sqrt 5}{2},$ $\beta = \dfrac{1-\sqrt 5}{2}$ とおく.
$\left|\dfrac{\beta}{\alpha}\right| = \dfrac{\sqrt 5-1}{\sqrt 5+1} < 1$ から
\[\begin{aligned}
\lim\limits_{n \to \infty}\frac{F_{n+1}}{F_n} &= \lim\limits_{n \to \infty}\frac{\alpha ^{n+1}-\beta ^{n+1}}{\alpha ^n-\beta ^n} = \lim\limits_{n \to \infty}\frac{\alpha -\beta\left(\dfrac{\beta}{\alpha}\right) ^n}{1-\left(\dfrac{\beta}{\alpha}\right) ^n} \\
&= \frac{\alpha -\beta\cdot 0}{1-0} = \alpha = \frac{1+\sqrt 5}{2}
\end{aligned}\]
である.
参考
無理数 $\dfrac{1+\sqrt 5}{2}$ は「黄金数」(golden number), 比 $1:\dfrac{1+\sqrt 5}{2}$ (約 $3:5$) は「黄金比」(golden ratio) と呼ばれる.
「黄金比」は最も美しい比であると言われ, 多くの美術作品の中にこの比を見ることができる.
問題《ペル方程式の解の成分の比の極限》
「ペル方程式」$x^2-2y^2 = 1$ の正の整数解 $(x,y)$ のうち $x$ の値が $n$ 番目に小さいもの $(x_n,y_n)$ は
\[ (x_n,y_n) = \left(\frac{(3\!+\!2\sqrt 2)^n+(3\!-\!2\sqrt 2)^n}{2},\frac{(3\!+\!2\sqrt 2)^n-(3\!-\!2\sqrt 2)^n}{2\sqrt 2}\right)\]
と表されることが知られている (証明はこちらを参照).
極限 $\lim\limits_{n \to \infty}\dfrac{x_n}{y_n}$ を求めよ.
(参考: 香川医大)
解答例
$0 < \dfrac{3-2\sqrt 2}{3+2\sqrt 2} < 1$ であるから,
\[\begin{aligned}
\lim\limits_{n \to \infty}\frac{x_n}{y_n} &= \lim\limits_{n \to \infty}\frac{(3+2\sqrt 2)^n+(3-2\sqrt 2)^n}{(3+2\sqrt 2)^n-(3-2\sqrt 2)^n}\cdot\sqrt 2 \\
&= \sqrt 2\lim\limits_{n \to \infty}\frac{1+\left(\dfrac{3-2\sqrt 2}{3+2\sqrt 2}\right) ^n}{1-\left(\dfrac{3-2\sqrt 2}{3+2\sqrt 2}\right) ^n} \\
&= \sqrt 2\cdot\frac{1+0}{1-0} = \sqrt 2
\end{aligned}\]
である.
参考
$d$ を平方数でない正の整数とする.
「ペル方程式」$x^2-dy^2 = 1$ の正の整数解 $(x,y)$ のうち $x$ の値が $n$ 番目に小さいもの $(x_n,y_n)$ は定数 $\varepsilon\,(> 1)$ を用いて
\[ (x_n,y_n) = \left(\frac{\varepsilon ^n+\varepsilon ^{-n}}{2},\frac{\varepsilon ^n-\varepsilon ^{-n}}{2\sqrt d}\right)\]
と表され,
\[\begin{aligned}
\lim\limits_{n \to \infty}\frac{x_n}{y_n} &= \lim\limits_{n \to \infty}\frac{\varepsilon ^n+\varepsilon ^{-n}}{\varepsilon ^n-\varepsilon ^{-n}}\cdot\sqrt d \\
&= \sqrt d\lim\limits_{n \to \infty}\frac{1+\varepsilon ^{-2n}}{1-\varepsilon ^{-2n}} \\
&= \sqrt d\cdot\frac{1+0}{1-0} = \sqrt d
\end{aligned}\]
が成り立つ.
いろいろな数列の極限
問題《無理数の連分数展開にまつわる数列の極限》
$\{ a_n\}$ を初期条件 $a_0 = 1$ と漸化式
\[ a_{n+1} = 1+\frac{1}{1+a_n}\]
で定まる数列とする.
- (1)
- 数列 $\{ a_n\}$ が $\alpha$ に収束すると仮定して, $\alpha$ の値を求めよ.
- (2)
- 数列 $\{ a_n\}$ が (1) の値に収束することを示せ.
解答例
- (1)
- 漸化式により, \[\begin{aligned} \alpha &= 1+\frac{1}{1+\alpha} \\ \alpha (1+\alpha ) &= (1+\alpha )+1 \\ \alpha ^2 &= 2 \end{aligned}\] であり, $a_n > 0$ から $\alpha \geqq 0$ であるので, \[\alpha = \sqrt 2\] である.
- (2)
- \[\begin{aligned} &|\sqrt 2-a_{n+1}| = \left|\sqrt 2-\left( 1+\frac{1}{1+a_n}\right)\right| \\ &= \left|\frac{(\sqrt 2-1)(1+a_n)-1}{1+a_n}\right| = \left|\frac{(\sqrt 2-2)+(\sqrt 2-1)a_n}{1+a_n}\right| \\ &= \left| -\frac{(\sqrt 2-1)(\sqrt 2-a_n)}{1+a_n}\right| = \frac{(\sqrt 2-1)|\sqrt 2-a_n|}{1+a_n} \\ &< (\sqrt 2-1)|\sqrt 2-a_n| \end{aligned}\] であるから, \[\begin{aligned} &|\sqrt 2-a_n| \leqq (\sqrt 2-1)^n|\sqrt 2-a_0| = (\sqrt 2-1)^{n+1} \\ &-(\sqrt 2-1)^{n+1} \leqq \sqrt 2-a_n \leqq (\sqrt 2-1)^{n+1} \end{aligned}\] が成り立つ. $|\sqrt 2-1| < 1$ から左辺と右辺は $0$ に収束するので, 挟みうちの原理により, \[\lim\limits_{n \to \infty}(\sqrt 2-a_n) = 0, \quad \lim\limits_{n \to \infty}a_n = \sqrt 2\] である.
別解
\[ a_n = \sqrt 2\cdot\frac{1-(-1)^n(\sqrt 2-1)^{2(n+1)}}{1+(-1)^n(\sqrt 2-1)^{2(n+1)}}\]
であり (こちらを参照), $|(-1)^n(\sqrt 2-1)^2| < 1$ であるから,
\[\lim\limits_{n \to \infty}a_n = \sqrt 2\cdot\frac{1-0}{1+0} = \sqrt 2\]
である.
参考
$\sqrt 2$ は
\[\sqrt 2 = 1+\frac{1}{2+\dfrac{1}{2+\dfrac{1}{\ddots}}}\]
と「連分数展開」される (こちらを参照).
問題《算術幾何平均に関する極限》
$a,$ $b$ を $a \geqq b \geqq 0$ なる実数として, 数列 $\{ a_n\},$ $\{ b_n\}$ を
\[ a_1 = a, \quad b_1 = b, \quad a_{n+1} = \frac{a_n+b_n}{2}, \quad b_{n+1} = \sqrt{a_nb_n}\]
で定める.
- (1)
- すべての正の整数 $n$ に対して $a_n \geqq b_n$ を示せ.
- (2)
- すべての正の整数 $n$ に対して $\sqrt{a_n}-\sqrt{b_n} \leqq \sqrt{a_n-b_n}$ を示せ.
- (3)
- 極限値 $\lim\limits_{n \to \infty}(a_n-b_n)$ を求めよ.
(参考: $2016$ 九州大, $2010$ 北海道大)
解答例
- (1)
- 仮定から $a_1 = a \geqq b = b_1$ であり, \[\begin{aligned} &a_{n+1}-b_{n+1} = \frac{a_n+b_n}{2}-\sqrt{a_nb_n} \\ &= \frac{a_n-2\sqrt{a_nb_n}+b_n}{2} = \frac{(\sqrt{a_n}-\sqrt{b_n})}{2} \geqq 0 \end{aligned}\] から $a_{n+1} \geqq b_{n+1}$ であるので, すべての正の整数 $n$ に対して $a_n \geqq b_n$ である.
- (2)
- (1) の結果により \[\begin{aligned} &(\sqrt{a_n-b_n})^2-(\sqrt{a_n}-\sqrt{b_n})^2 \\ &= (a_n-b_n)-(a_n-2\sqrt{a_nb_n}+b_n) \\ &= 2\sqrt{a_nb_n}-2b_n \\ &= 2(\sqrt{a_n}-\sqrt{b_n})\sqrt{b_n} \geqq 0 \end{aligned}\] であるから, \[ (\sqrt{a_n}-\sqrt{b_n})^2 \leqq (\sqrt{a_n-b_n})^2\] つまり \[\sqrt{a_n}-\sqrt{b_n} \leqq \sqrt{a_n-b_n}\] が成り立つ ($\sqrt{a_n}-\sqrt{b_n} \geqq 0$ に注意).
- (3)
- (1) の式変形と (2) の結果により \[\begin{aligned} a_{n+1}-b_{n+1} &= \frac{a_n+b_n}{2}-\sqrt{a_nb_n} = \frac{(\sqrt{a_n}-\sqrt{b_n})^2}{2} \\ &\leqq \frac{(\sqrt{a_n-b_n})^2}{2} = \frac{a_n-b_n}{2} \end{aligned}\] であるので, 数学的帰納法により \[ 0 \leqq a_n-b_n \leqq \frac{a_1-b_1}{2^{n-1}}\] が成り立つ. 左側の不等号は (1) の結果による. 右辺は $0$ に収束するから, 挟みうちの原理により \[\lim_{n \to \infty}(a_n-b_n) = 0\] が成り立つ.
参考
- $a_1 \geqq b_1 \geqq 0$ と連立漸化式 \[ a_{n+1} = \dfrac{a_n+b_n}{2}, \quad b_{n+1} = \sqrt{a_nb_n} \quad \cdots [*]\] で定まる数列 $\{ a_n\},$ $\{ b_n\}$ は共通の値に収束することが知られており, その極限値は $a_1,$ $b_1$ の「算術幾何平均」(arithmetic-geometric mean) と呼ばれる. $[*]$ において, $a_n \geqq b_n$ を仮定すると \[ a_n \geqq a_{n+1} = \dfrac{a_n+b_n}{2} \geqq \sqrt{a_nb_n} = b_{n+1} \geqq b_n\] となるから, \[ a_1 \geqq \cdots \geqq a_n \geqq \cdots \geqq b_n \geqq \cdots \geqq b_1\] が成り立つ. よって, $\{ a_n\}$ は $b_1$ 以上の値をとる単調減少数列であり, $\{ b_n\}$ は $a_1$ 以下の値をとる単調増加数列である. 常に一定値以下の値をとる単調増加数列 (または常に一定値以上の値をとる単調減少数列) は収束することが知られているから, $\{ a_n\}$ と $\{ b_n\}$ は収束する. よって, $2a_{n+1} = a_n+b_n$ の両辺の極限をとると, $2\lim\limits_{n \to \infty}a_n = \lim\limits_{n \to \infty}a_n+\lim\limits_{n \to \infty}b_n$ つまり $\lim\limits_{n \to \infty}a_n = \lim\limits_{n \to \infty}b_n$ が得られる.
- 正の数 $a,$ $b$ の「算術幾何平均」は \[\frac{\pi}{2}\div\int_0^{\frac{\pi}{2}}\frac{d\theta}{\sqrt{a^2\cos ^2\theta +b^2\sin ^2\theta}}\] に等しいことが知られている (分母の定積分は,「楕円積分」と呼ばれるタイプの定積分であり, 一般に計算が難しい).
- 円周率の近似値の計算方法として,「算術幾何平均」を使った次の公式が知られている: $[*]$ において $a_1 = 1,$ $b_1 = \dfrac{1}{\sqrt 2}$ とし, 数列 $\{ c_n\}$ を \[ c_1 = \dfrac{1}{4}, \quad c_{n+1} = c_n-2^n(a_n-a_{n+1})^2\] で定めると, $\pi = \lim\limits_{n \to \infty}\dfrac{a_{n+1}{}^2}{c_n}$ が成り立つ.
問題《ニュートン法》
$d > 1,$ $x_1 > \sqrt d$ とし, 点 $(x_n,x_n{}^2-d)$ における放物線 $y = x^2-d$ の接線と $x$ 軸の交点の $x$ 座標を $x_{n+1}$ として, 数列 $\{ x_n\}$ を定める.
次のことを示せ.
- (1)
- $x_{n+1} = \dfrac{x_n{}^2+d}{2x_n}$ が成り立つ.
- (2)
- $x_{n+1}-\sqrt d < \dfrac{x_n-\sqrt d}{2}$ が成り立つ.
- (3)
- $\lim\limits_{n \to \infty}x_n = \sqrt d$ である.
(参考: $1995$ 名古屋大)
解答例
- (1)
- 点 $(x_n,x_n{}^2-d)$ における放物線 $y = x^2-d$ の接線の方程式は,
\[ y = 2x_n(x-x_n)+x_n{}^2-d\]
つまり
\[ y = 2x_nx-x_n{}^2-d\]
である.
この直線と $x$ 軸の交点の $x$ 座標が $x_{n+1}$ であるから,
\[\begin{aligned}
0 &= 2x_nx_{n+1}-x_n{}^2-d \\
2x_nx_{n+1} &= x_n{}^2+d \quad \cdots [1]
\end{aligned}\]
が成り立つ.
$x_1 > 0$ と $[1]$ から $x_n > 0$ であることに注意すると (証明は数学的帰納法), $[1]$ の両辺を $2x_n$ で割ることで, 求める等式が得られる.
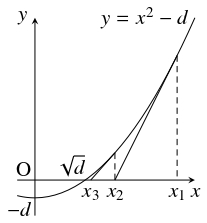
- (2)
- (1) から, \[ x_{n+1}-\sqrt d = \frac{x_n{}^2-2x_n\sqrt d+d}{2x_n} = \frac{(x_n-\sqrt d)^2}{2x_n} \quad \cdots [2]\] が成り立つ. $x_1-\sqrt d > 0$ と $[2]$ から $x_n > x_n-\sqrt d > 0$ であることに注意すると (証明は数学的帰納法), \[ x_{n+1}-\sqrt d < \frac{(x_n-\sqrt d)^2}{2(x_n-\sqrt d)} = \frac{x_n-\sqrt d}{2} \quad \cdots [3]\] が得られる.
- (3)
- $[3]$ から \[ 0 < x_n-\sqrt d \leqq \frac{x_1-\sqrt d}{2^{n-1}}\] であり, 右辺は $0$ に収束するから, 挟みうちの原理により $\lim\limits_{n \to \infty}(x_n-\sqrt d) = 0$ つまり $\lim\limits_{n \to \infty}x_n = \sqrt d$ である.
参考
グラフが上に凸または下に凸である微分可能な関数 $f(x)$ について, $f(x) = 0$ の解は, 点 $(x_{n-1},f(x_{n-1}))$ における $y = f(x)$ の接線と $x$ 軸の交点の $x$ 座標 $x_n$ の極限として求めることができる.
この $f(x) = 0$ の解の近似値の計算法は「ニュートン法」(Newton's method) と呼ばれる (こちらを参照).
問題《縮小関数で定まる数列の極限》
数列 $\{ a_n\}$ を $a_1 = \sqrt 2,$ $a_{n+1} = \sqrt{2+a_n}$ で定める.
- (1)
- $\sqrt 2 \leqq a_n < 2$ が成り立つことを示せ.
- (2)
- $a_n < a_{n+1}$ が成り立つことを示せ.
- (3)
- $2-a_{n+1} \leqq \dfrac{1}{2+\sqrt{2+\sqrt 2}}(2-a_n)$ が成り立つことを示せ.
- (4)
- 極限値 $\lim\limits_{n \to \infty}a_n$ を求めよ.
(参考: 京都府立大)
解答例
- (1)
- $\sqrt 2 \leqq a_n < 2\ \cdots [1]$ を数学的帰納法で示す.
- (i)
- $n = 1$ のとき. $a_1 = \sqrt 2$ から, $[1]$ が成り立つ.
- (ii)
- $n = k$ ($k$: 正の整数) のとき $[1]$ が成り立つとする. このとき, \[\begin{aligned} 2+\sqrt 2 &\leqq 2+a_k < 2+2 \\ \sqrt{2+\sqrt 2} &\leqq \sqrt{2+a_k} < \sqrt{2+2} \\ \sqrt 2 &\leqq a_{k+1} < 2 \end{aligned}\] となり, $n = k+1$ のとき $[1]$ が成り立つ.
- (2)
- $[1]$ から \[\begin{aligned} a_{n+1}-a_n &= \sqrt{2+a_n}-a_n \\ &= \frac{(\sqrt{2+a_n}-a_n)(\sqrt{2+a_n}+a_n)}{\sqrt{2+a_n}+a_n} \\ &= \frac{2+a_n-a_n{}^2}{\sqrt{2+a_n}+a_n} \\ &= \frac{(1+a_n)(2-a_n)}{\sqrt{2+a_n}+a_n} > 0 \end{aligned}\] であるので, \[ a_n < a_{n+1} \quad \cdots [2]\] が成り立つ.
- (3)
- $[2]$ から $a_1 \leqq \cdots \leqq a_n$ よって $a_1 \leqq a_n$ であるので, \[\begin{aligned} 2-a_{n+1} &= 2-\sqrt{2+a_n} = \frac{2-a_n}{2+\sqrt{2+a_n}} \\ &\leqq \frac{2-a_n}{2+\sqrt{2+a_1}} = \frac{1}{2+\sqrt{2+\sqrt 2}}(2-a_n) \quad \cdots [3] \end{aligned}\] が成り立つ.
- (4)
- $[1],$ $[3]$ から \[ 0 < 2-a_n \leqq \cdots \leqq \left(\frac{1}{2+\sqrt{2+\sqrt 2}}\right) ^{n-1}(2-a_1)\] が成り立ち, 右辺は $0$ に収束するから, $\lim\limits_{n \to \infty}(2-a_n) = 0$ つまり $\lim\limits_{n \to \infty}a_n = 2$ である.
参考
- 区間 $I$ を定義域とし, $I$ の中に値をとる連続関数 $f(x)$ について, \[ |f(x_2)-f(x_1)| \leqq r|x_2-x_1| \quad (x_1,\ x_2 \in I)\] が成り立つような定数 $r$ が $0 \leqq r < 1$ の範囲に存在するとき, $f(x)$ を「縮小関数」(shrinking function) と呼ぶ. このような関数について, 次の「バナッハの不動点定理」の成り立つことが知られている: $f(x)$ が「縮小関数」であるならば, 方程式 $f(x) = x$ の実数解 $x = \alpha$ がただ $1$ つ存在して, 漸化式 $a_{n+1} = f(a_n)$ と任意の初期条件で定まる数列 $\{ a_n\}$ は $\alpha$ に収束する. ここで, $\alpha$ は $f(x)$ の「不動点」(fixed point) と呼ばれる. $f(x) = \sqrt{2+x}\ (x > 0)$ は「縮小関数」であり, $\sqrt{2+x} = x$ の解は $x = 2$ であるから,「バナッハの不動点定理」により, 問題の数列 $\{ a_n\}$ は $2$ に収束する. この $f(x)$ が「縮小関数」であることは, $0 < x_1 < x_2$ のとき, 平均値の定理により \[\frac{f(x_2)-f(x_1)}{x_2-x_1} = f'(c)\] つまり \[\frac{\sqrt{2+x_2}-\sqrt{2+x_1}}{x_2-x_1} = \frac{1}{2\sqrt{2+c}}\] を満たす実数 $c$ が $x_1 < c < x_2$ の範囲に存在し, よって \[ |\sqrt{2+x_2}-\sqrt{2+x_1}| = \frac{1}{2\sqrt{2+c}}|x_2-x_1| < \frac{1}{2\sqrt 2}|x_2-x_1|\] が成り立つことから示される.
- ちなみに, $\cos\dfrac{\pi}{2^{n+1}} = \dfrac{a_n}{2}$ からも, \[\lim\limits_{n \to \infty}a_n = 2\lim\limits_{n \to \infty}\cos\dfrac{\pi}{2^{n+1}} = 2\cos 0 = 2\] であることがわかる. 本問の数列は,「ヴィエトの公式」(Viète's formula) \[\pi = 2\cdot\frac{2}{\sqrt 2}\cdot\frac{2}{\sqrt{2+\sqrt 2}}\cdot\frac{2}{\sqrt{2+\sqrt{2+\sqrt 2}}}\cdot\cdots\] に現れる (こちらを参照). つまり, $\dfrac{2}{\pi}$ は $2$ の「多重平方根」とその極限値である $2$ の比をすべて掛け合わせた値である.
- 一般に, 正の数 $a$ に対して, $a_1 = \sqrt a,$ $a_{n+1} = \sqrt{a+a_n}$ で定まる数列 $\{ a_n\}$ は $\dfrac{1+\sqrt{1+4a}}{2}$ に収束する.
- $1$ より大きい実数 $a$ に対して, $a_1 = \sqrt a,$ $a_{n+1} = \sqrt{aa_n}$ で定まる数列 $\{ a_n\}$ は $a$ に収束する.
問題《$nr^n$ とじゃんけんの勝者数の期待値の極限》
$n$ を $2$ 以上の整数とする.
- (1)
- $h > 0$ のとき, $(1+h)^n > \dfrac{n(n-1)}{2}h^2$ であることを示せ.
- (2)
- $0 < r < 1$ のとき, $\lim\limits_{n \to \infty}nr^n = 0$ であることを示せ.
- (3)
- $n$ 人で $1$ 回だけじゃんけんをするとき, 勝者の数 $X_n$ の期待値は $E(X_n) = \dfrac{n(2^{n-1}-1)}{3^{n-1}}$ であることが知られている (こちらを参照). 極限値 $\lim\limits_{n \to \infty}E(X_n)$ を求めよ.
解答例
- (1)
- $h > 0$ のとき, 二項定理により, \[\begin{aligned} (1+h)^n &= 1+nh+\frac{n(n-1)}{2}h^2+\cdots +h^n \\ &> \frac{n(n-1)}{2}h^2 \end{aligned}\] が成り立つ.
- (2)
- $0 < r < 1$ とする. $\dfrac{1}{r} > 1$ であるから, $\dfrac{1}{r} = 1+h$ $(h > 0)$ とおく. $n \geqq 2$ のとき, (1) の結果から \[ 0 < nr^n = \frac{n}{(1+h)^n} < \frac{n}{\dfrac{n(n-1)}{2}h^2} = \frac{2}{(n-1)h^2}\] が成り立つ. $n \to \infty$ のとき右辺は $0$ に収束するから, 挟みうちの原理により \[\lim\limits_{n \to \infty}nr^n = 0\] である.
- (3)
- \[ 0 < E(X_n) = \frac{n(2^{n-1}-1)}{3^{n-1}} < \frac{n\cdot 2^{n-1}}{3^{n-1}} = \frac{3}{2}n\left(\frac{2}{3}\right) ^n\] であり, (2) の結果により右辺は $0$ に収束するから, 挟みうちの原理により \[\lim\limits_{n \to \infty}E(X_n) = 0\] である.
参考
一般に, $|r| < 1$ のとき, すべての多項式 $f(x)$ に対して $\lim\limits_{n \to \infty}f(n)r^n = 0$ が成り立つ.
問題《オイラーの定数にまつわる数列の極限》
数列 $\left\{\displaystyle\sum\limits_{k = 1}^n\frac{1}{k}-\log n\right\}$ は有限の極限値 $\gamma$ を持つことが知られている.
数列 $\left\{\displaystyle\sum\limits_{k = 1}^n\frac{1}{2k-1}-c\log n\right\}$ が収束するとき, 極限値 $\gamma '$ と定数 $c$ の値を求めよ.
(参考: $1982$ 防衛医科大)
解答例
\[\begin{aligned}
&\sum\limits_{k = 1}^{2n}\frac{1}{k}-\log 2n \\
&= \left(\sum\limits_{k = 1}^n\frac{1}{2k-1}-c\log n\right) +\left(\sum\limits_{k = 1}^n\frac{1}{2k}-\frac{1}{2}\log n\right) \\
&\qquad +c\log n+\frac{1}{2}\log n-\log n-\log 2 \\
&= \left(\sum\limits_{k = 1}^n\frac{1}{2k-1}-c\log n\right) +\frac{1}{2}\left(\sum\limits_{k = 1}^n\frac{1}{k}-\log n\right) \\
&\qquad +\left( c-\frac{1}{2}\right)\log n-\log 2 \quad \cdots [1]
\end{aligned}\]
であるから, 数列 $\left\{\displaystyle\sum\limits_{k = 1}^n\frac{1}{2k-1}-c\log n\right\}$ が収束するとき $\left\{\left( c-\dfrac{1}{2}\right)\log n\right\}$ は収束しなければならず
\[ c = \dfrac{1}{2}\]
となる.
このとき, $[1]$ の両辺の極限をとると
が得られる.
| $\gamma = \gamma '+\dfrac{1}{2}\gamma -\log 2$ つまり $\gamma ' = \dfrac{\gamma}{2}+\log 2$ |
参考
- 極限値 $\gamma = \lim\limits_{n \to \infty}\left(\displaystyle\sum\limits_{k = 1}^n\frac{1}{k}-\log n\right)$ は「オイラーの定数」(Euler's constant) と呼ばれ, 数学の諸分野で現れる重要な定数であるが, 有理数, 無理数のどちらであるかさえもわかっていない ($2019$ 年 $8$ 月現在).
- 「ある定数より各項が大きい単調減少数列は収束する」という事実を使うと, 極限値 $\gamma$ が実際に存在することは, $a_n = \displaystyle\sum\limits_{k = 1}^n\frac{1}{k}-\log n$ とおくと, \[\begin{aligned} a_n &= \sum\limits_{k = 1}^n\frac{1}{k}-\int _1^n\frac{dx}{x} \\ &\geqq \sum\limits_{k = 1}^n\frac{1}{k}-\sum\limits_{k = 1}^n\frac{1}{k+1} = \sum_{k = 1}^n\frac{1}{k(k+1)} > 0 \end{aligned}\] となり, \[\begin{aligned} a_n-a_{n+1} &= \sum\limits_{k = 1}^n\dfrac{1}{k}-\log n-\sum\limits_{k = 1}^{n+1}\dfrac{1}{k}+\log (n+1) \\ &= \log\frac{n+1}{n}-\frac{1}{n+1} \\ &= \int _n^{n+1}\frac{dx}{x}-\frac{1}{n+1} > 0 \end{aligned}\] から $a_n > a_{n+1}$ となることからわかる.
無限級数
こちらを参照.
