無理関数
無理関数
問題《無理関数を含む不等式とその応用》
$a,$ $b$ を正の数とする.
- (1)
- $a < b$ のとき, 不等式 $\sqrt x > \dfrac{\sqrt b-\sqrt a}{b-a}(x-a)+\sqrt a$ を解け.
- (2)
- $\dfrac{a+b}{2} \geqq \sqrt{ab}$ が成り立つことを示し, 等号成立条件を求めよ.
解答例
- (1)
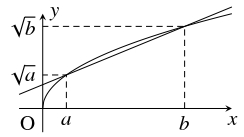
- 曲線 $y = \sqrt x$ が $2$ 点 $(a,\sqrt a),$ $(b,\sqrt b)$ を結ぶ直線 $y = \dfrac{\sqrt b-\sqrt a}{b-a}(x-a)+\sqrt a$ より上方にあるような $x$ の値の範囲 $a < x < b$ が求める解である.
- (2)
- (i)
- $a < b$ のとき. $x = \dfrac{a+b}{2}$ のとき (1) の不等式の右辺は \[\begin{aligned} &\frac{\sqrt b-\sqrt a}{b-a}\left(\frac{a+b}{2}-a\right) +\sqrt a \\ &= \frac{\sqrt b-\sqrt a}{b-a}\cdot\frac{b-a}{2}+\sqrt a = \frac{\sqrt a+\sqrt b}{2} \end{aligned}\] となるから, $\sqrt{\dfrac{a+b}{2}} > \dfrac{\sqrt a+\sqrt b}{2}$ よって $\dfrac{a+b}{2} > \dfrac{a+2\sqrt{ab}+b}{4}$ である. ゆえに, $\dfrac{a+b}{4} > \dfrac{\sqrt{ab}}{2}$ つまり $\dfrac{a+b}{2} > \sqrt{ab}$ が成り立つ.
- (ii)
- $b < a$ のとき. (i) で $a,$ $b$ を入れ替えると, $\dfrac{a+b}{2} > \sqrt{ab}$ が得られる.
- (iii)
- $a = b$ のとき. $\dfrac{a+b}{2} = \sqrt{ab} = a$ が成り立つ.
別解
- (1)
- $x \geqq 0$ とする.
$x-a = (\sqrt x+\sqrt a)(\sqrt x-\sqrt a)$ であるから, 与式は
\[ (\sqrt x+\sqrt a)(\sqrt x-\sqrt a) < (\sqrt a+\sqrt b)(\sqrt x-\sqrt a) \quad \cdots [1]\]
と変形できる.
- (i)
- $0 \leqq x < a$ のとき. $\sqrt x < \sqrt a$ つまり $\sqrt x-\sqrt a < 0$ から, \[\begin{aligned} [1] &\iff \sqrt x+\sqrt a > \sqrt a+\sqrt b \\ &\iff \sqrt x > \sqrt b \iff x > b \end{aligned}\] となり, $b < x < a$ となる. 仮定から, 不等式の解は存在しない.
- (ii)
- $x = a$ のとき. $[1]$ の両辺は $0$ となるから, 不等式の解は存在しない.
- (iii)
- $a < x$ のとき. $\sqrt x > \sqrt a$ つまり $\sqrt x-\sqrt a > 0$ から, \[\begin{aligned} [1] &\iff \sqrt x+\sqrt a < \sqrt a+\sqrt b \\ &\iff \sqrt x < \sqrt b \iff x < b \end{aligned}\] となる. よって, 不等式の解は $a < x < b$ である.
参考
相加・相乗平均の不等式は, $y = \sqrt x$ のグラフが上に凸であるという性質を反映している.
