無限級数
無限等比級数
定理《無限等比級数の収束・発散》
$a,$ $r$ を実数とし, $\{ a_n\}$ を初項 $a,$ 公比 $r$ の無限等比数列とする.
- (1)
- $a \neq 0,$ $|r| < 1$ ならば, \[\sum_{n = 1}^\infty a_n = \frac{a}{1-r}\] が成り立つ.
- (2)
- $a \neq 0,$ $|r| \geqq 1$ のとき, $\displaystyle\sum_{n = 1}^\infty a_n$ は発散する.
- (3)
- $a = 0$ のとき, $\displaystyle\sum_{n = 1}^\infty a_n = 0$ である.
証明
等比数列の和の公式により,
\[\sum_{k = 1}^nar^{n-1} = \begin{cases}
\dfrac{a(1-r^n)}{1-r} & (r \neq 1), \\
na & (r = 1)
\end{cases}\]
が成り立つ.
$\{ r^n\}$ は, $|r| < 1$ のとき $0$ に収束し, $r > 1$ のとき発散し, $r \leqq -1$ のとき振動する.
これから, 求める結果が得られる.
問題《黄金長方形にまつわる無限等比級数》
$\varphi = \dfrac{1+\sqrt 5}{2}$ のとき, 無限等比級数 $\displaystyle\sum_{n = 0}^\infty (\varphi -1)^{2n}$ の和を求めよ.
解答例
$1 < \sqrt 5 < 3$ から $0 < -1+\sqrt 5 < 2$ であり,
\[ 0 < \varphi -1 = \dfrac{-1+\sqrt 5}{2} < 1, \quad 0 < (\varphi -1)^2 < 1\]
であるので, 無限等比級数 $\displaystyle\sum_{n = 0}^\infty (\varphi -1)^{2n}$ は収束して, 求める和は
\[\begin{aligned}
\sum_{n = 0}^\infty (\varphi -1)^{2n} &= \frac{1}{1-(\varphi -1)^2} = \frac{1}{2\varphi -\varphi ^2} \\
&= \frac{1}{2\varphi -(\varphi +1)} \quad (\because\varphi ^2 -\varphi -1 = 0) \\
&= \frac{1}{\varphi -1} = \frac{2}{\sqrt 5-1} = \frac{2(\sqrt 5+1)}{(\sqrt 5-1)(\sqrt 5+1)} \\
&= \frac{2(\sqrt 5+1)}{4} = \frac{1+\sqrt 5}{2} = \varphi
\end{aligned}\]
である.
参考
短辺の長さが $1,$ 長辺の長さが $\varphi = \dfrac{1+\sqrt 5}{2}$ の長方形 $R$ の端から $1$ 辺の長さが $1$ の正方形を取り除くと, 短辺の長さが $\varphi -1,$ 長辺の長さが $1$ の長方形 $R'$ が得られるが,
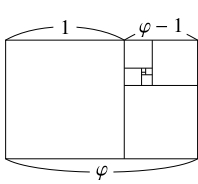 さらに, 残りの長方形の端から正方形を取り除くという操作を無限に繰り返すことによって,
長方形 $R$ のすべての部分を取りつくすことができる.
辺の長さの比が $1:\varphi$ の長方形を「黄金長方形」(golden rectangle) と呼ぶ.
さらに, 残りの長方形の端から正方形を取り除くという操作を無限に繰り返すことによって,
長方形 $R$ のすべての部分を取りつくすことができる.
辺の長さの比が $1:\varphi$ の長方形を「黄金長方形」(golden rectangle) と呼ぶ.
$\varphi ^2-\varphi -1 = 0$ つまり $1:\varphi = (\varphi -1):1$
から, $R$ と $R'$ は $1:(\varphi -1)$ の比で相似である.

問題《コッホ雪片》
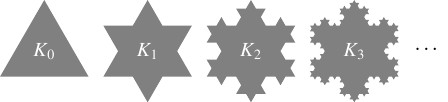
$1$ 辺の長さが $1$ の正三角形を $K_0$ として, 次のような規則で多角形 $K_n$ $(n \geqq 0)$ を順次定めていく.
多角形 $K_n$ の各辺において, 辺を $3$ 等分する $2$ 点を頂点とするような正三角形を $K_n$ の外側に貼り合わせ, できた多角形を $K_{n+1}$ とする.
- (1)
- 多角形 $K_n$ の周の長さを $L_n$ とおく. 極限 $\lim\limits_{n \to \infty}L_n$ を求めよ.
- (2)
- 多角形 $K_n$ の面積を $S_n$ とおく. 極限 $\lim\limits_{n \to \infty}S_n$ を求めよ.
(参考: $2010$ 北海道大ほか)
解答例
- (1)
- $K_n$ から $K_{n+1}$ を作るとき, $K_n$ の各辺はその $\dfrac{1}{3}$ 倍の長さの辺 $4$ 本になるから,
$L_{n+1} = \dfrac{4}{3}L_n$ が成り立つ.
よって, \[ L_n = \left(\frac{4}{3}\right) ^nL_0 = 3\cdot\left(\frac{4}{3}\right) ^n \quad (\because L_0 = 3)\] から, $\lim\limits_{n \to \infty}L_n = \infty$ である.
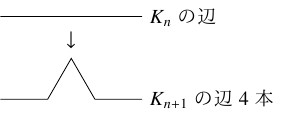
- (2)
- $K_n$ から $K_{n+1}$ を作るとき, $1$ 辺の長さが $\dfrac{1}{3^{n+1}}$ の正三角形 $3\cdot 4^n$ 個が貼り合わせられるから, \[\begin{aligned} S_{n+1}-S_n &= (3\cdot 4^n)\cdot\left(\frac{1}{3^{n+1}}\right)^2S_0 \\ &= \frac{\sqrt 3}{12}\left(\frac{4}{9}\right) ^n \quad \left(\because S_0 = \frac{\sqrt 3}{4}\right) \end{aligned}\] が成り立つ. よって, 求める極限は, \[\begin{aligned} \lim\limits_{n \to \infty}S_n &= \lim\limits_{n \to \infty}S_{n+1} \\ &= \lim\limits_{n \to \infty}\left\{ S_0+\sum_{k = 0}^n(S_{k+1}-S_k)\right\} \\ &= S_0+\sum_{n = 0}^\infty (S_{n+1}-S_n) \\ &= \frac{\sqrt 3}{4}+\frac{\sqrt 3}{12}\sum_{n = 0}^\infty\left(\frac{4}{9}\right) ^n \\ &= \frac{\sqrt 3}{4}+\frac{\sqrt 3}{12}\cdot\frac{1}{1-\dfrac{4}{9}} \\ &= \frac{2\sqrt 3}{5} \end{aligned}\] である.
参考
- 本問の操作を無限に繰り返すことで得られる図形 (つまり $K_0,$ $K_1,$ $\cdots,$ $K_n,$ $\cdots$ の共通部分) を「コッホ雪片」(Koch snowflake) と呼ぶ.
- 単位正方形から始めて, 直前に貼り合わせた正方形の各辺の中央外側に $3$ 分の $1$ の大きさの正方形を貼り合わせるという操作を無限に繰り返すことで得られる多角形の面積の極限値は $\dfrac{5}{3}$ である (参考: お茶の水女子大).
- 正三角形から各辺の中点を結ぶ正三角形を取り除き, 新たにできたすべての小三角形から同様に正三角形を取り除くという操作を無限に続けると,「シェルピンスキーのギャスケット」(Sierpinski gasket) と呼ばれる図形が得られる.

- これらの図形は, 一部が全体に相似であるという性質をもち, 「フラクタル図形」(fractal, 定義は省略) の代表的な例である.
問題《メンガーのスポンジ》
$1$ 辺の長さが $1$ の立方体を $M_0$ として, 次のような規則で立体 $M_n$ $(n \geqq 0)$ を順次定めていく.
$M_n$ を構成する $20^{n-1}$ 個の立方体をそれぞれ互いに合同な $27$ 個の小立方体に分割して, その中心の小立方体と各面の中央の小立方体を取り除き, 合計 $20^n$ 個の小立方体からなる立体を $M_{n+1}$ とする.
- (1)
- 立体 $M_n$ の体積を $V_n$ とおく. 極限 $\lim\limits_{n \to \infty}V_n$ を求めよ.
- (2)
- 立体 $M_n$ の表面積を $S_n$ とおく. 極限 $\lim\limits_{n \to \infty}S_n$ を求めよ.
解答例
- (1)
- 上記の操作により, $M_n$ を構成する各立方体は互いに合同な $27$ 個の小立方体に分割されて $7$ 個が取り除かれるから, \[ V_{n+1} = \frac{20}{27}V_n\] が成り立つ. また, $V_0 = 1^3 = 1$ であるから \[ V_n = \left(\frac{20}{27}\right) ^nV_0 = \left(\frac{20}{27}\right) ^n\] であり, \[\lim\limits_{n \to \infty}V_n = 0\] である.
- (2)
- $M_n$ と $M_0$ に共通する表面の面積の総和を $a_n$ とおき, $b_n = S_n-a_n$ とおく. このとき, \[ a_{n+1} = \frac{8}{9}a_n, \quad a_0 = 6\cdot 1^2 = 6\] から \[ a_n = \left(\frac{8}{9}\right) ^na_0 = 6\left(\frac{8}{9}\right) ^n\] である. また, \[\begin{aligned} b_{n+1} &= 24\cdot\frac{1}{6}\cdot\frac{a_n}{9}+20\cdot\frac{b_n}{9} \\ &= \frac{20}{9}b_n+\frac{8}{3}\left(\frac{8}{9}\right) ^n \quad \cdots [1] \end{aligned}\] であるから, \[ b_{n+2} = \frac{20}{9}b_{n+1}+\frac{8}{3}\left(\frac{8}{9}\right) ^{n+1} \quad \cdots [2]\] が成り立つ. よって, $[2]-[1]\times\dfrac{8}{9}$ から \[ b_{n+2}-\frac{8}{9}b_{n+1} = \frac{20}{9}\left( b_{n+1}-\frac{8}{9}b_n\right)\] であり, \[ b_0 = 0, \quad b_1 = \dfrac{24}{9} = \dfrac{8}{3}\] であるので, \[\begin{aligned} b_{n+1}-\frac{8}{9}b_n &= \left( b_1-\frac{8}{9}b_0\right)\left(\frac{20}{9}\right) ^n = \frac{8}{3}\left(\frac{20}{9}\right) ^n \\ b_{n+1} &= \frac{8}{9}b_n+\frac{8}{3}\left(\frac{20}{9}\right) ^n \quad \cdots [3] \end{aligned}\] が成り立つ. $[1]$ に $[3]$ を代入して整理すると, \[\begin{aligned} \frac{12}{9}b_n &= \frac{8}{3}\left(\frac{20}{9}\right) ^n-\frac{8}{3}\left(\frac{8}{9}\right) ^n \\ b_n &= 2\left(\frac{20}{9}\right) ^n-2\left(\frac{8}{9}\right) ^n \end{aligned}\] が得られる. よって, \[ S_n = a_n+b_n = 2\left(\frac{20}{9}\right) ^n+4\left(\frac{8}{9}\right) ^n\] であるから, \[\lim\limits_{n \to \infty}S_n = \infty\] である.
参考
本問の操作を無限に繰り返すことで得られる図形 (つまり $M_0,$ $M_1,$ $\cdots,$ $M_n,$ $\cdots$ の共通部分) を「メンガーのスポンジ」(Menger sponge) と呼ぶ.
いろいろな無限級数
問題《$nr^n$ の無限和と硬貨を投げる回数の期待値》
- (1)
- $0 < r < 1$ とする. 無限級数 $\displaystyle\sum_{n = 1}^\infty nr^n$ の和を求めよ. $\lim\limits_{n \to \infty}nr^n = 0$ であること (こちらを参照) は証明なしに使ってよい.
- (2)
- $1$ 枚の硬貨を $n$ 回投げるとき, $n$ 回目に初めて表が出る確率を $p_n$ とおく. 無限級数 $\displaystyle\sum_{n = 1}^\infty np_n$ の和を求めよ.
解答例
- (1)
- 第 $n$ 項までの部分和を \[ S_n = 1\cdot r+2r^2+\cdots +nr^n\] とおく. 両辺に $r$ を掛けると \[ rS_n = 1\cdot r^2+\cdots +(n-1)r^n+nr^{n+1}\] となるから, 辺々を引くと \[\begin{aligned} (1-r)S_n &= r+r^2+\cdots +r^n-nr^{n+1} \\ &= \frac{r(1-r^n)}{1-r}-nr^{n+1} \end{aligned}\] が得られる. 両辺を $1-r$ で割ると \[ S_n = \frac{r(1-r^n)}{(1-r)^2}-\frac{r}{1-r}nr^n\] となるから, \[\sum_{n = 1}^\infty nr^n \!=\! \lim\limits_{n \to \infty}S_n \!=\! \frac{r}{(1-r)^2} \quad \left(\because\lim\limits_{n \to \infty}r^n \!=\! \lim\limits_{n \to \infty}nr^n \!=\! 0\right)\] である.
- (2)
- $n$ 回目に初めて表が出る確率は \[ p_n = \left(\frac{1}{2}\right) ^{n-1}\cdot\frac{1}{2} = \left(\frac{1}{2}\right) ^n\] であるから, (1) の結果により \[\sum_{n = 1}^\infty np_n = \sum_{n = 1}^\infty n\left(\frac{1}{2}\right) ^n = \frac{\dfrac{1}{2}}{\left( 1-\dfrac{1}{2}\right) ^2} = 2\] である.
参考
- $0 < p < 1$ なる実数 $p$ について, \[ P(X = n) = (1-p)^{n-1}p \quad \cdots [*]\] ($n$: 正の整数) で定まる確率分布を「幾何分布」(geometric distribution) と呼ぶ. ここで, 各回の成功する確率が $p,$ 失敗する確率が $1-p$ である反復試行において, $[*]$ は $n$ 回目に初めて成功する確率を表す.
- 上記の「幾何分布」に従う確率変数 $X$ の期待値は, \[\begin{aligned} E(X) &= \sum_{n = 1}^\infty n(1-p)^{n-1}p = \frac{p}{1-p}\sum_{n = 1}^\infty n(1-p)^n \\ &= \frac{p}{1-p}\cdot\frac{1-p}{\{ 1-(1-p)\} ^2} = \frac{1}{p} \end{aligned}\] である. 特に, 無限級数 $\displaystyle\sum_{n = 1}^\infty n\left(\frac{1}{2}\right) ^n$ は, 表が出るまで硬貨を投げるときの試行の回数の期待値を表す.
問題《クーポン・コレクターの問題の期待値》
- (1)
- $0 < r < 1$ とする. 無限級数 $\displaystyle\sum_{n = 1}^\infty nr^{n-1}$ の和を求めよ. $\lim\limits_{n \to \infty}nr^n = 0$ であること (こちらを参照) は証明なしに使ってよい.
- (2)
- ある試行において, 事象 $A_1,$ $\cdots,$ $A_n$ のいずれかが等確率で起こるとする. この試行を繰り返して, 事象 $A_1,$ $\cdots,$ $A_n$ のうち $k$ 個 $(0 \leqq k \leqq n-1)$ が起こった状態からさらに $m$ 回繰り返すとき, $m$ 回目に初めて別の事象が起こる確率を $p_m$ とおき, \[ E_k = \displaystyle\sum_{m = 1}^\infty mp_m\] と定める. $\displaystyle\sum_{k = 1}^n\frac{1}{k}$ を用いて $\displaystyle\sum_{k = 0}^{n-1}E_k$ の値を表せ.
解答例
- (1)
- 第 $n$ 項までの部分和を \[ S_n = 1\cdot 1+2r+\cdots +nr^{n-1}\] とおく. 両辺に $r$ を掛けると \[ rS_n = 1\cdot r+\cdots +(n-1)r^{n-1}+nr^n\] となるから, 辺々を引くと \[\begin{aligned} (1-r)S_n &= 1+r+\cdots +r^{n-1}-nr^n \\ &= \frac{1-r^n}{1-r}-nr^n \end{aligned}\] が得られる. 両辺を $1-r$ で割ると \[ S_n = \frac{1-r^n}{(1-r)^2}-\frac{nr^n}{1-r}\] となるから, \[\sum_{n = 1}^\infty nr^{n-1} \!=\! \lim\limits_{n \to \infty}S_n \!=\! \frac{1}{(1-r)^2} \quad \left(\because\lim\limits_{n \to \infty}r^n \!=\! \lim\limits_{n \to \infty}nr^n \!=\! 0\right)\] である.
- (2)
- $p_m$ は, $m-1$ 回はすでに起こった $k$ 個の事象以外は起こらず, その次に残り $n-k$ 個のうち $1$ つの事象が起こる確率であるから, \[ p_m = \left(\dfrac{k}{n}\right) ^{m-1}\dfrac{n-k}{n}\] である. よって, \[\begin{aligned} E_k &= \sum_{m = 1}^\infty mp_m = \sum_{m = 1}^\infty m\left(\frac{k}{n}\right) ^{m-1}\frac{n-k}{n} \\ &= \frac{n-k}{n}\left( 1-\dfrac{k}{n}\right) ^{-2} = \frac{n-k}{n}\left(\dfrac{n-k}{n}\right) ^{-2} \\ &= \frac{n}{n-k} \end{aligned}\] である. ここで第 $3$ の等号では, (1) により \[\sum_{m = 1}^\infty m\left(\frac{k}{n}\right) ^{m-1} = \left( 1-\dfrac{k}{n}\right) ^{-2}\] であることを使った (これは $k = 0$ のときも成り立つ). ゆえに, \[\sum_{k = 0}^{n-1}E_k = \sum_{k = 0}^{n-1}\frac{n}{n-k} = n\sum_{k = 1}^n\dfrac{1}{k}\] である.
参考
- 正の整数全体を値域とする確率変数 $W$ の期待値は \[ E(W) = \sum_{m = 1}^\infty m\,P(W = m)\] で定義される. (2) の試行を繰り返すとき, 事象 $A_1,$ $\cdots,$ $A_n$ のうち $k$ 個 $(0 \leqq k \leqq n-1)$ が起こった状態から別の $1$ 個が起こるまでにかかる試行の回数 $X_k$ の期待値は \[ E(X_k) = \frac{n}{n-k}\] である.
- (2) の試行を $X$ 回繰り返したときに初めて $A_1,$ $\cdots,$ $A_n$ がすべて $1$ 回以上起こったとするとき, \[ X = \sum_{k = 0}^{n-1}X_k\] であるから, 期待値の線形性により \[ E(X) = \sum_{k = 0}^{n-1}E(X_k) = \sum_{k = 0}^{n-1}\frac{n}{n-k} = n\sum_{k = 1}^n\frac{1}{k}\] である. 例えば, $n$ 種類のアイテムのうち $1$ 種類がランダムに封入されたカプセル・トイで全種類のアイテムを集める ($n$ 面のさいころですべての目を出す) には, 平均的にこの回数繰り返せばよいと見込まれる. この種の問題はしばしば「クーポン・コレクターの問題」(coupon collector's problem) または「食玩問題」と呼ばれる.
- 無限級数 $\displaystyle\lim_{n \to \infty}\left(\sum_{k = 1}^n\frac{1}{k}-\log n\right)$ は収束し, その和 $\gamma = 0.57721\cdots$ を「オイラーの定数」(Euler's constant) と呼ぶ. \[\lim_{n \to \infty}n\sum_{k = 1}^n\frac{1}{k}\!-\!\lim_{n \to \infty}n(\log n\!+\!\gamma ) \!=\! \lim_{n \to \infty}\left(\sum_{k = 1}^n\frac{1}{k}\!-\!\log n\!-\!\gamma\right) \!=\! 0\] であるから, $n$ が十分に大きいとき, $E(X)$ は近似的に $n(\log n+\gamma )$ に等しいと言える.
- $n$ が小さいときの $E(X)$ の値は, 次の表の通りである.
$n$ $1$ $2$ $3$ $4$ $E(X)$ $1$ $3$ $\dfrac{11}{2}$
$= 5.5$$\dfrac{25}{3}$
$= 8.33\cdots$$n$ $5$ $6$ $7$ $8$ $E(X)$ $\dfrac{137}{12}$
$= 11.41\cdots$$\dfrac{147}{10}$
$= 14.7$$\dfrac{363}{20}$
$= 18.15$$\dfrac{761}{35}$
$= 21.74\cdots$$n$ $9$ $10$ $11$ $12$ $E(X)$ $\dfrac{7129}{280}$
$= 25.46\cdots$$\dfrac{7381}{252}$
$= 29.28\cdots$$\dfrac{83711}{2520}$
$= 33.21\cdots$$\dfrac{86021}{2310}$
$= 37.23\cdots$
問題《正接がフィボナッチ数の逆数である角の和》
数列 $\{ F_n\}$ を $F_1 = F_2 = 1,$ $F_{n+2} = F_n+F_{n+1}$ で定め, $\tan x$ $\left( -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\right)$ の逆関数を $\arctan x$ で表す.
- (1)
- $F_{n+1}F_{n+2}-(-1)^n = F_n(F_{n+1}+F_{n+2})$ が成り立つことを示せ.
- (2)
- $\arctan\dfrac{1}{F_{2n}} = \arctan\dfrac{1}{F_{2n+1}}+\arctan\dfrac{1}{F_{2n+2}}$ が成り立つことを示せ.
- (3)
- 無限級数 $\displaystyle\sum_{n = 1}^\infty\arctan\dfrac{1}{F_{2n-1}}$ の和を求めよ.
(参考: $2013$ 京都府立医科大)
解答例
各正の整数 $n$ に対して, $\theta _n = \arctan\dfrac{1}{F_n}$ とおく.
つまり, $\theta _n$ を $\tan\theta _n = \dfrac{1}{F_n},$ $0 < \theta _n < \dfrac{\pi}{2}$ を満たす実数とする.
- (1)
- $a_n = F_{n+1}F_{n+2}-F_n(F_{n+1}+F_{n+2})$ とおく. \[\begin{aligned} a_n &= F_{n+1}F_{n+2}-F_nF_{n+1}-F_nF_{n+2} \\ &= F_{n+1}F_{n+2}-F_nF_{n+1}-F_nF_{n+2} \\ &= F_{n+1}(F_{n+2}-F_n)-F_nF_{n+2} \\ &= F_{n+1}{}^2-F_nF_{n+2} \end{aligned}\] であるから, \[\begin{aligned} a_{n+1} &= F_{n+2}{}^2-F_{n+1}F_{n+3} \\ &= F_{n+2}{}^2-F_{n+1}(F_{n+1}+F_{n+2}) \\ &= F_{n+2}{}^2-F_{n+1}{}^2-F_{n+1}F_{n+2} \\ &= F_{n+2}(F_{n+2}-F_{n+1})-F_{n+1}{}^2 \\ &= F_{n+2}F_n-F_{n+1}{}^2 \\ &= -a_n \end{aligned}\] が成り立つ. よって, $\{ a_n\}$ は初項 \[ F_2{}^2-F_1F_3 = 1^2-1\cdot (1+1) = -1,\] 公比 $-1$ の等比数列であるから, \[ a_n = (-1)^n\] つまり \[ F_{n+1}F_{n+2}-(-1)^n = F_n(F_{n+1}+F_{n+2}) \quad \cdots [1]\] が成り立つ.
- (2)
- 定義により $\{ F_n\}$ は $n \geqq 2$ において単調増加であり, $F_3 = 2> 1$ であるから, $n \geqq 3$ において $F_n > 1,$ $0 < \dfrac{1}{F_n} < 1$ つまり \[ 0 < \theta _n < \frac{\pi}{4}\] が成り立つ. よって, 各正の整数 $n$ に対して, \[ 0 < \theta _{2n+1} < \frac{\pi}{4}, \quad 0 < \theta _{2n+2} < \frac{\pi}{4}\] であるから, \[ 0 < \theta _{2n+1}+\theta _{2n+2} < \frac{\pi}{2}\] が成り立つ. さらに, \[\begin{aligned} &\tan\left(\theta _{2n+1}+\theta _{2n+2}\right) \\ &= \frac{\tan\theta _{2n+1}+\tan\theta _{2n+2}}{1-\tan\theta _{2n+1}\tan\theta _{2n+2}} = \frac{\dfrac{1}{F_{2n+1}}+\dfrac{1}{F_{2n+2}}}{1-\dfrac{1}{F_{2n+1}}\cdot\dfrac{1}{F_{2n+2}}} \\ &= \frac{F_{2n+1}+F_{2n+2}}{F_{2n+1}F_{2n+2}-1} = \frac{F_{2n+1}+F_{2n+2}}{F_{2n+1}F_{2n+2}-(-1)^{2n}} \\ &= \frac{F_{2n+1}+F_{2n+2}}{F_{2n}(F_{2n+1}+F_{2n+2})} \quad (\because [1]) \\ &= \frac{1}{F_{2n}} \end{aligned}\] が成り立つ. 以上から, \[\theta _{2n} = \theta _{2n+1}+\theta _{2n+2} \quad \cdots [2]\] つまり \[\arctan\frac{1}{F_{2n}} = \arctan\frac{1}{F_{2n+1}}+\arctan\frac{1}{F_{2n+2}}\] が成り立つ.
- (3)
- $n \geqq 2$ のとき $[2]$ により \[\begin{aligned} \sum_{k = 1}^n\theta _{2k-1} &= \theta _1+\sum_{k = 1}^{n-1}\theta _{2k+1} = \theta _1+\sum_{k = 1}^{n-1}(\theta _{2k}-\theta _{2k+2}) \\ &= \theta _1+\theta _2-\theta _{2n} = \frac{\pi}{2}-\theta _{2n} \quad \left(\because\theta _1 = \theta _2 = \frac{\pi}{4}\right) \end{aligned}\] であり, $\lim\limits_{n \to \infty}F_n = \infty$ から \[\lim\limits_{n \to \infty}\tan\theta _n = \lim\limits_{n \to \infty}\frac{1}{F_n} = 0\] よって \[\lim\limits_{n \to \infty}\theta _n = 0\] であるので, \[\begin{aligned} \sum_{n = 1}^\infty\arctan\dfrac{1}{F_{2n-1}} &= \sum_{n = 1}^\infty\theta _{2n-1} = \lim\limits_{n \to \infty}\sum_{k = 1}^n\theta _{2k-1} \\ &= \lim\limits_{n \to \infty}\left(\frac{\pi}{2}-\theta _{2n}\right) = \frac{\pi}{2} \end{aligned}\] である.
参考
- 初期条件 $F_1 = F_2 = 1$ と漸化式 $F_{n+2} = F_n+F_{n+1}$ で定まる数列 $\{ F_n\}$ を「フィボナッチ数列」(Fibonacci sequence) と呼ぶ. $F_{n+1}{}^2-F_nF_{n+2} = (-1)^n$ は, $F_{n+2} = F_n+F_{n+1}$ と同値であり (こちらを参照), 「カッシーニの公式」(Cassini's identity) として知られている.
- $\arctan\dfrac{1}{F_2} = \arctan\dfrac{1}{F_3}+\arctan\dfrac{1}{F_4}$ から \[\frac{\pi}{4} = \arctan\frac{1}{2}+\arctan\frac{1}{3}\] が成り立つ.
- $\arctan\dfrac{1}{F_1}+\arctan\dfrac{1}{F_3}+\arctan\dfrac{1}{F_5} = \arctan\dfrac{1}{F_1}+\arctan\dfrac{1}{F_2}-\arctan\dfrac{1}{F_6}$ つまり $\arctan\dfrac{1}{F_2} = \arctan\dfrac{1}{F_3}+\arctan\dfrac{1}{F_5}+\arctan\dfrac{1}{F_6}$ から \[\frac{\pi}{4} = \arctan\frac{1}{2}+\arctan\frac{1}{5}+\arctan\frac{1}{8}\] が成り立つ.
- これらは, 円周率の近似値の計算への応用をもつ「マチンの公式」(Machin's formula) \[\frac{\pi}{4} = 4\arctan\frac{1}{5}-\arctan\frac{1}{239}\] (こちらを参照) の類似である.
問題《シルヴェスター数列の逆数の総和》
初期条件 $s_1 = 2$ と漸化式
\[ s_{n+1} = s_n{}^2-s_n+1 \quad \cdots [1]\]
で定まる「シルヴェスター数列」$\{ s_n\}$ について,
\[\begin{aligned}
s_{n+1} &= s_1\cdots s_n+1 \quad \cdots [2], \\
\sum_{k = 1}^n\frac{1}{s_k} &= 1-\frac{1}{s_{n+1}-1} \quad \cdots [3]
\end{aligned}\]
の成り立つことが知られている (こちらを参照).
- (1)
- $n \geqq 3$ のとき \[ s_n-1 > 2^{2^{n-2}} \quad \cdots [4]\] が成り立つことを示せ.
- (2)
- 無限級数 $\displaystyle\sum_{n = 1}^\infty\frac{1}{s_n}$ の和を求めよ.
(参考: $2017$ 千葉大)
解答例
- (1)
- $n \geqq 3$ のとき $[4]$ が成り立つことを数学的帰納法で示す.
- (i)
- $n = 3$ のとき. $s_1 = 2$ と $[2]$ により \[ s_2 = 2+1 = 3, \quad s_3 = 2\cdot 3+1 = 7\] であるから, \[ s_3-1 = 6 > 4 = 2^{2^1}\] であり, $[4]$ が成り立つ.
- (ii)
- $n = k$ ($k$: $3$ 以上の整数) のとき $[4]$ が成り立つとする. このとき, \[\begin{aligned} s_{k+1}-1 &= s_k{}^2-s_k = s_k(s_k-1) \quad (\because [1]) \\ &> (s_k-1)^2 \\ &> (2^{2^{k-2}})^2 = 2^{2^{k-1}} \end{aligned}\] となるから, $n = k+1$ のとき $[4]$ が成り立つ.
- (2)
- $n \geqq 3$ のとき, $[3],$ $[4]$ により \[ 0 < 1-\sum_{k = 1}^n\frac{1}{s_k} = \frac{1}{s_{n+1}-1} < \frac{1}{2^{2^{n-1}}}\] が成り立ち, 右辺は $0$ に収束するから, 挟みうちの原理により \[ 1-\sum_{n = 1}^\infty\frac{1}{s_n} = 0, \quad \sum_{n = 1}^\infty\frac{1}{s_n} = 1\] である.
参考
- $s_1 = 2,$ $s_{n+1} = s_n{}^2-s_n+1$ で定まる数列 $\{ s_n\}$ は「シルヴェスター数列」(Sylvester sequence) と呼ばれる (注意: $s_{n+1} = s_1\cdots s_n+1$ を定義の漸化式に採用することもあり, $s_0 = 2$ とする流儀もある).
- 次の「カーティスの定理」が知られている: 連立不等式 \[\frac{1}{x_1}+\cdots +\frac{1}{x_n} < 1, \quad 0 < x_1 < \cdots < x_n\] の整数解に対して, $\dfrac{1}{x_1}+\cdots +\dfrac{1}{x_n}$ は $(x_1,\cdots,x_n) = (s_1,\cdots,s_n)$ のとき最大値をとる ($n = 2,$ $3$ の場合はこちらを参照).
- (2) において, 部分和からなる数列 $\displaystyle\left\{\sum_{k = 1}^n\frac{1}{s_k}\right\}$ は $1$ 未満の値をとり, 単調増加であるから, 常に一定値以下の値をとる単調増加数列は収束するという定理により, $\displaystyle\sum_{n = 1}^\infty\frac{1}{s_n}$ は収束する.
問題《調和級数の発散》
- (1)
- $\displaystyle\sum_{n = 1}^\infty\frac{1}{n} = \infty$ であることを示せ.
- (2)
- $0 < s \leqq 1$ のとき, $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^s} = \infty$ であることを示せ.
解答例
- (1)
- \[\begin{aligned} \sum_{k = 1}^{2^m}\frac{1}{k} &= 1+\sum_{l = 1}^m\sum_{k = 2^{l-1}+1}^{2^l}\frac{1}{k} \\ &\geqq 1+\sum_{l = 1}^m2^{l-1}\cdot\frac{1}{2^l} = 1+\sum_{l = 1}^m\frac{1}{2} \\ &= 1+\frac{m}{2} \end{aligned}\] において, $m \to \infty$ のとき右辺は $\infty$ に発散するから, 追い出しの原理により \[\sum_{n = 1}^\infty\frac{1}{n} = \lim_{m \to \infty}\sum_{k = 1}^{2^m}\frac{1}{k} = \infty\] である.
- (2)
- $0 < s \leqq 1$ とする. 正の整数 $k$ に対して $k^s \leqq k$ から $\dfrac{1}{k^s} \geqq \dfrac{1}{k}$ であるので, \[\sum_{k = 1}^n\frac{1}{k^s} \geqq \sum_{k = 1}^n\frac{1}{k}\] が成り立つ. (1) から右辺は $\infty$ に発散するので, 追い出しの原理により \[\sum_{n = 1}^\infty\frac{1}{n^s} = \lim_{n \to \infty}\sum_{k = 1}^n\frac{1}{n^s} = \infty\] である.
参考
- 無限級数 $\displaystyle\sum_{n = 1}^\infty a_n$ が収束するとき $\displaystyle\lim\limits_{n \to \infty}a_n = 0$ が成り立つが, この逆は必ずしも成り立たない.
- $\displaystyle\sum_{n = 1}^\infty\frac{1}{n}$ を「調和級数」(harmonic series), $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^s}$ を「汎調和級数」と呼ぶ. $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^s}$ の定義域を複素数の範囲に拡げることで「リーマン・ゼータ関数」(Riemann zeta function) が定義される.
- $s > 1$ のときの $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^s}$ の挙動についてはこちらを参照.
