分数関数
分数関数
問題《周長と面積が等しい長方形》
縦の長さが $x,$ 横の長さが $y$ の長方形の周の長さと面積が等しいとする.
- (1)
- $y$ を $x$ の関数で表し, そのグラフをかけ.
- (2)
- $x,$ $y$ が整数のとき, $x,$ $y$ の値を求めよ.
解答例
- (1)
- $2x+2y = xy$ から,
\[\begin{aligned}
(x-2)y &= 2x \\
y &= \dfrac{2x}{x-2} \\
y &= \dfrac{4}{x-2}+2
\end{aligned}\]
である.
よって, この関数のグラフは双曲線 $y = \dfrac{4}{x}$ を $x$ 軸方向に $2,$ $y$ 軸方向に $2$ だけ平行移動した曲線で, その概形は次の通りである.
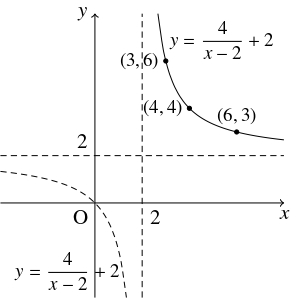
- (2)
- $x,$ $y$ が整数のとき, $\dfrac{4}{x-2}$ は整数であるので,
\[ x-2 = \pm 1,\ \pm 2,\ \pm 4\]
から,
$x = -2,$ $0,$ $1,$ $3,$ $4,$ $6$ である.
$x > 0$ から $x = -2,$ $0$ は不適で, $x = 1,$ $3,$ $4,$ $6$ である.
このとき, $y = -2,$ $6,$ $4,$ $3$ であるが, $y > 0$ から $y = -2$ は不適で, \[ (x,y) = (3,6),\ (4,4),\ (6,3)\] である.
参考
- 周の長さと面積が等しい図形を「等長積図形」と呼ぶ (equable shape の和訳として提案したい).
- 各辺の長さが整数である「等長積三角形」, つまり周の長さと面積が等しい「ヘロンの三角形」については, こちらを参照.
問題《分数関数を含む方程式と不等式》
$a,$ $b,$ $c,$ $d$ は実数で, $ad-bc < 0,$ $c \neq 0$ とする.
このとき, 次のことを示せ.
- (1)
- $x$ の方程式 $\dfrac{ax+b}{cx+d} = x$ は $x = -\dfrac{d}{c}$ の両側に $1$ つずつ実数解をもつ.
- (2)
- (1) の $2$ 解を $\alpha,$ $\beta$ $\left(\alpha < -\dfrac{d}{c} < \beta\right)$ とおくとき, $\alpha < x < \beta$ かつ $x \neq -\dfrac{d}{c}$ ならば, $\dfrac{ax+b}{cx+d} < \alpha$ または $\beta < \dfrac{ax+b}{cx+d}$ である.
(参考: 東京工業大)
解答例
- (1)
- \[\frac{ax+b}{cx+d} = x \quad \cdots [1]\] の両辺に $c(cx+d)$ を掛けて整理すると, $x$ の $2$ 次方程式 \[ c^2x^2+c(d-a)x-bc = 0 \quad \cdots [2]\] が得られる. 左辺に $-\dfrac{d}{c}$ を代入すると, 仮定から \[ d^2-d(d-a)-bc = ad-bc < 0\] となるので, $[2]$ は $x = -\dfrac{d}{c}$ の両側に $1$ つずつ実数解をもつ. それらの解は $[1]$ の分母 $cx+d$ を $0$ にしないから, $[1]$ は $x = -\dfrac{d}{c}$ の両側に $1$ つずつ実数解をもつ.
- (2)
- $y = \dfrac{ax+b}{cx+d}$ とおく. $(y-\alpha )(y-\beta ) > 0$ を示せばよい. \[ y = \frac{a}{c}-\frac{ad-bc}{c(cx+d)}\] であるので, \[\begin{aligned} y\!-\!\alpha &= \frac{ad\!-\!bc}{c(c\alpha \!+\!d)}\!-\!\frac{ad\!-\!bc}{c(cx\!+\!d)} \!=\! \frac{(ad\!-\!bc)(x\!-\!\alpha )}{(cx\!+\!d)(c\alpha\!+\!d)}, \\ y\!-\!\beta &= \frac{(ad\!-\!bc)(x\!-\!\beta )}{(cx\!+\!d)(c\beta\!+\!d)} \end{aligned}\] と $\alpha < x < \beta,$ $\alpha < -\dfrac{d}{c} < \beta$ から \[ (y-\alpha )(y-\beta ) = \frac{(ad-bc)^2(x-\alpha )(x-\beta )}{(cx+d)^2(c\alpha +d)(c\beta +d)} > 0\] が成り立つ.
