$H$ は座標軸に関して対称であるから, 第 $1$ 象限の部分が $y = \dfrac{b}{a}x$ を漸近線にもつことを示せば十分である. $H$ は第 $1$ 象限において \[ y = \frac{b}{a}\sqrt{x^2-a^2}\] で表され, \[\begin{aligned} &\left| y-\frac{b}{a}x\right| = \frac{b}{a}x-\frac{b}{a}\sqrt{x^2-a^2} \\ &= \frac{b}{a}(x-\sqrt{x^2-a^2}) = \frac{b}{a}\cdot\frac{(x-\sqrt{x^2-a^2})(x+\sqrt{x^2-a^2})}{x+\sqrt{x^2-a^2}} \\ &= \frac{b}{a}\cdot\frac{x^2-(x^2-a^2)}{x+\sqrt{x^2-a^2}} = \frac{b}{a}\cdot\frac{a^2}{x+\sqrt{x^2-a^2}} \\ &\to 0 \quad (x \to \infty ) \end{aligned}\] が成り立つから, $H$ は $y = \dfrac{b}{a}x$ を漸近線にもつ.

　まず, $\lim\limits_{x \to +0}\dfrac{\sin x}{x} = 1$ を示す. $0 < x < \dfrac{\pi}{2}$ の範囲で考えれば十分である. 点 $\mathrm O$ を中心とする半径 $1,$ 中心角 $x$ の扇形 $\mathrm{OAB}$ を考える. 点 $\mathrm B$ から線分 $\mathrm{OA}$ に下ろした垂線の足を $\mathrm H$ とおき, 点 $\mathrm A$ を通り $\mathrm{HB}$ と平行な直線が直線 $\mathrm{OB}$ と交わる点を $\mathrm T$ とおく. 扇形 $\mathrm{OAB}$ の面積を $S$ とおくと, \[\triangle\mathrm{OAB} < S < \triangle\mathrm{OAT}\] となる. $\mathrm{BH} = \sin x,$ $\mathrm{AT} = \tan x$ であるから, \[\frac{1}{2}\cdot 1\cdot \sin x < \frac{1}{2}\cdot 1^2\cdot x < \frac{1}{2}\cdot 1\cdot\tan x\] となり, \[\sin x < x < \tan x\] となる. 各辺を $\sin x$ で割ると \[ 1 < \frac{x}{\sin x} < \frac{1}{\cos x}\] となるから, 各辺の逆数をとると \[ 1 > \frac{\sin x}{x} > \cos x\] となる. $\lim\limits_{x \to +0}\cos x = 1$ であるから, 挟みうちの原理により \[\lim\limits_{x \to +0}\frac{\sin x}{x} = 1 \quad \cdots [1]\] が成り立つ. よって, \[\lim\limits_{x \to -0}\frac{\sin x}{x} = \lim\limits_{x \to -0}\frac{\sin (-x)}{-x} = \lim\limits_{x \to +0}\frac{\sin x}{x} = 1 \quad \cdots [2]\] が成り立つ. $[1],$ $[2]$ から, 求める等式が得られる.

(1)

倍角の公式により \[\cos\frac{\theta}{2^k}\sin\frac{\theta}{2^k} = \frac{1}{2}\cos\frac{\theta}{2^{k-1}}\] であるから, \[\begin{aligned} \cos\frac{\theta}{2}\cdots\cos\frac{\theta}{2^n}\sin\frac{\theta}{2^n} &= \frac{1}{2}\cos\frac{\theta}{2}\cdots\cos\frac{\theta}{2^{n-1}}\sin\frac{\theta}{2^{n-1}} \\ &= \cdots \\ &= \frac{1}{2^{n-1}}\cos\frac{\theta}{2}\sin\frac{\theta}{2} \\ &= \frac{1}{2^n}\sin\theta \end{aligned}\] が成り立つ.

(2)

(1) の結果に $\theta = \dfrac{\pi}{2}$ を代入すると, \[ \cos\frac{\pi}{4}\cdots\cos\frac{\pi}{2^{n+1}}\sin\frac{\pi}{2^{n+1}} = \frac{1}{2^n}\] から \[\begin{aligned} \cos\frac{\pi}{4}\cdots\cos\frac{\pi}{2^{n+1}} &= \frac{1}{2^n}\div\sin\frac{\pi}{2^{n+1}} \\ &= \frac{2}{\pi}\cdot\frac{\pi}{2^{n+1}}\div\sin\frac{\pi}{2^{n+1}} \\ &\to \frac{2}{\pi}\cdot 1 = \frac{2}{\pi} \quad (n \to \infty ) \end{aligned}\] となる.

　円の半径が $1$ であるとしても一般性を失わない. このとき, 円の中心を $\mathrm O$ とおき, $\theta = \angle\mathrm{OAR}$ とおく. 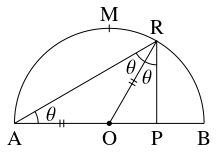反射角は入射角に等しいことと $\mathrm{OR} = \mathrm{OA}$ から \[\angle\mathrm{ORP} = \angle\mathrm{ORA} = \theta\] であるので, \[\angle\mathrm{OPR} = \pi -3\theta\] が成り立つ. よって, $\triangle\mathrm{OPR}$ に正弦定理を適用すると, \[\frac{\mathrm{OP}}{\sin\theta} = \frac{1}{\sin (\pi -3\theta )} = \frac{1}{\sin 3\theta}\] が得られる. 点 $\mathrm R$ を点 $\mathrm B$ に限りなく近づけていくとき, 点 $\mathrm P$ が近づいていく点を $\mathrm P_0$ とすると, $\theta \to +0$ であるから, \[\begin{aligned} \mathrm{OP}_0 &= \lim_{\theta \to +0}\mathrm{OP} = \lim_{\theta \to +0}\frac{\sin\theta}{\sin 3\theta} = \frac{1}{3}\lim_{\theta \to +0}\frac{\sin\theta}{\theta}\cdot\frac{3\theta}{\sin 3\theta} \\ &= \frac{1}{3}\cdot 1\cdot\frac{1}{1} = \frac{1}{3} \end{aligned}\] となる. よって, 求める距離の比は \[\mathrm{AP}_0:\mathrm P_0\mathrm B = \left( 1+\frac{1}{3}\right) :\left( 1-\frac{1}{3}\right) = 2:1\] である.

　正 $2n$ 角形は頂角の大きさが $\dfrac{2\pi}{2n} = \dfrac{\pi}{n}$ の二等辺三角形 $2n$ 個に分けられるから, 単位円に内接するとき, その $1$ 辺の長さは \[ 2\sin\left(\frac{1}{2}\cdot\frac{\pi}{n}\right) = 2\sin\frac{\pi}{2n}\] である. また, 正 $2n$ 角形の外角の大きさは $\dfrac{2\pi}{2n} = \dfrac{\pi}{n}$ である.

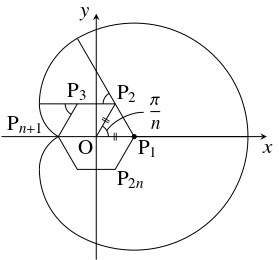
(1)

ひもの長さは, 正 $2n$ 角形の周の長さの半分であり, $n$ 本分の辺の長さに等しいから, \[ L = 2n\sin\frac{\pi}{2n}\] である.

(2)

原点を $\mathrm O$ とおく. $\triangle\mathrm O\mathrm P_1\mathrm P_2$ において $\angle\mathrm P_1$ の内角の大きさは \[\frac{1}{2}\left(\pi -\frac{\pi}{n}\right) = \dfrac{n-1}{2n}\pi,\] $\angle\mathrm P_1$ の外角の大きさは \[\pi -\frac{n-1}{2n}\pi = \frac{n+1}{2n}\pi\] であるから, \[\begin{aligned} T_0 &= \frac{1}{2}L^2\frac{n+1}{2n}\pi \\ &= \frac{1}{2}\left( 2n\sin\frac{\pi}{2n}\right) ^2\frac{n+1}{2n}\pi \\ &= n(n+1)\pi\sin ^2\frac{\pi}{2n} \end{aligned}\] である.

(3)

$1 \leqq k \leqq n-1$ とする. 頂点 $\mathrm P_{k+1}$ までひもを巻きつけたとき, ひもの可動部分の長さは \[ L-k\cdot 2\sin\frac{\pi}{2n} = 2(n-k)\sin\frac{\pi}{2n}\] であるから, \[\begin{aligned} T_k &= \frac{1}{2}\left\{ 2(n-k)\sin\frac{\pi}{2n}\right\} ^2\frac{\pi}{n} \\ &= \frac{2(n-k)^2}{n}\pi\sin ^2\frac{\pi}{2n} \end{aligned}\] である.

(4)

ヤギが動き回れる範囲は $x$ 軸に関して対称であるから, \[ S_{2n} = 2\left( T_0+\sum_{k = 1}^{n-1}T_k\right)\] である. ここで, \[\begin{aligned} \sum_{k = 1}^{n-1}T_k &= \sum_{k = 1}^{n-1}\frac{2(n-k)^2}{n}\pi\sin ^2\frac{\pi}{2n} \\ &= \frac{2\pi}{n}\sin ^2\frac{\pi}{2n}\sum_{k = 1}^{n-1}(n-k)^2 \\ &= \frac{2\pi}{n}\sin ^2\frac{\pi}{2n}\sum_{k = 1}^{n-1}k^2 \\ &= \frac{2\pi}{n}\sin ^2\frac{\pi}{2n}\cdot\frac{(n-1)n(2n-1)}{6} \\ &= \frac{(n-1)(2n-1)}{3}\pi\sin ^2\frac{\pi}{2n}, \\ T_0+\sum_{k = 1}^{n-1}T_k &= n(n+1)\pi\sin ^2\!\frac{\pi}{2n}+\frac{(n-1)(2n-1)}{3}\pi\sin ^2\!\frac{\pi}{2n} \\ &= \frac{3n(n+1)+(n-1)(2n-1)}{3}\pi\sin ^2\frac{\pi}{2n} \\ &= \frac{5n^2+1}{3}\pi\sin ^2\frac{\pi}{2n} \end{aligned}\] であるから, 求める面積は \[ S_{2n} = \frac{2(5n^2+1)}{3}\pi\sin ^2\frac{\pi}{2n}\] である.

(5)

\[\begin{aligned} S_{2n} &= \left(\frac{\pi}{2n}\right)^2\frac{2(5n^2+1)}{3}\pi\left(\frac{\sin\dfrac{\pi}{2n}}{\dfrac{\pi}{2n}}\right) ^2 \\ &= \frac{5n^2+1}{6n^2}\pi ^3\left(\frac{\sin\dfrac{\pi}{2n}}{\dfrac{\pi}{2n}}\right) ^2 \\ &\to \frac{5}{6}\pi ^3 \quad (n \to \infty ) \end{aligned}\] であるから, 求める極限値は $\lim\limits_{n \to \infty}S_{2n} = \dfrac{5}{6}\pi ^3$ である.