長さ $1$ の棒が入る円柱形の容器において, 底面の半径を $r,$ 高さを $h,$ 容積を $V$ とおく. 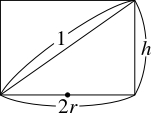このとき, $0 < h < 1$ であり, 三平方の定理により

$1^2 = (2r)^2+h^2$　つまり　$r^2 = \dfrac{1-h^2}{4}$

が成り立つ. \[\begin{aligned} V &= \pi r^2h = \frac{\pi}{4}(h-h^3), \\ \frac{dV}{dh} &= \frac{\pi}{4}(1-3h^2) \end{aligned}\] であるから, $V$ の増減は下表のようにまとめられる. したがって, $V$ は $h = \dfrac{1}{\sqrt 3}$ のとき極大かつ最大の値をとる. ゆえに, 底面の直径, 高さ, 棒の長さの比が \[ 2r:h:1 = \frac{2}{\sqrt 6}:\frac{1}{\sqrt 3}:1 = \sqrt 2:1:\sqrt 3\] であれば, 容積は最大になる.

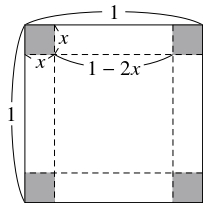
　$1$ 辺の長さが $1$ の正方形の紙で考える. 箱の高さを $x,$ 容積を $V$ とおく. このとき, 底面の $1$ 辺の長さは $1-2x$ であり, $0 < x < \dfrac{1}{2}$ である. \[\begin{aligned} V &= x(1-2x)^2 = 4x^3-4x^2+x, \\ \frac{dV}{dx} &= 12x^2-8x+1 = (2x-1)(6x-1) \end{aligned}\] であるから, $V$ の増減は下表のようにまとめられる. したがって, $V$ は $x = \dfrac{1}{6}$ のとき極大かつ最大の値をとる. ゆえに, 底面の $1$ 辺の長さと高さの比が $1-2\cdot\dfrac{1}{6}:\dfrac{1}{6} = 4:1$ であれば, 容積は最大になる.

　円に内接する最大の三角形は正三角形であるから (証明は省略), 半径 $1$ の球に内接する正三角柱 $\mathrm{ABC}$-$\mathrm{DEF}$ の体積 $V$ の最大値を求める. 底面の $1$ 辺の長さを $a,$ 球の中心を $\mathrm O$ とおき, $2\theta = \angle\mathrm{AOD}$ とおく.

(1)

$\theta$ を用いて $V$ を表す. 辺 $\mathrm{AD}$ の中点を $\mathrm M,$ $\triangle\mathrm{ABC}$ の重心を $\mathrm G$ とおく. 直角三角形 $\mathrm{OAM}$ に着目すると \[\cos\theta = \cos\angle\mathrm{AOM} = \frac{\mathrm{OM}}{\mathrm{OA}} = \frac{\mathrm{AG}}{1} = \dfrac{2}{3}\cdot\frac{\sqrt 3}{2}a = \frac{a}{\sqrt 3}\] となるから, $a$ は \[ a = \sqrt 3\cos\theta\] と表せる. また, この正三角柱の高さは $2\sin\theta$ であるから, 体積は \[\begin{aligned} V &= \frac{1}{2}a^2\sin 60^\circ\cdot 2\sin\theta \\ &= \frac{\sqrt 3}{2}\cdot (\sqrt 3\cos\theta )^2\cdot\sin\theta \\ &= \frac{3\sqrt 3}{2}\sin\theta\cos ^2\theta \end{aligned}\] と表せる.

(2)

$V$ の最大値を求め, 体積比を求める. $x = \sin\theta$ とおく. \[\frac{2}{3\sqrt 3}V = \sin\theta (1-\sin ^2\theta ) = \sin\theta -\sin ^3\theta = x-x^3\] であるから, この右辺を $f(x)$ とおく. \[ f'(x) = 1-3x^2\] であるから, $f(x)$ の増減は下表のようにまとめられる ($0 < x < 1$ に注意).

$x$	$0$	$\cdots$	$\dfrac{1}{\sqrt 3}$	$\cdots$	$1$
$f'(x)$		$+$	$0$	$-$
$f(x)$		$\nearrow$	極大	$\searrow$

よって, $f(x)$ は $x = \dfrac{1}{\sqrt 3}$ のとき極大かつ最大の値をとるから, $V$ の最大値は \[\frac{3\sqrt 3}{2}\cdot\frac{1}{\sqrt 3}\left( 1-\frac{1}{3}\right) = 1\] である. ゆえに, 求める体積比は, \[ 1\div\pi\cdot 1^2 = \dfrac{1}{\pi}\] である.

　扇形の半径を $1$ とし, できる円錐の底面の半径を $x$ とおく. このとき, 容器の高さ $h$ は三平方の定理により \[ h = \sqrt{1-x^2}\] であるから, 容器の容積 $V$ は \[ V = \frac{1}{3}\pi x^2h = \frac{1}{3}\pi x^2\sqrt{1-x^2}\] である. $f(x) = (x^2\sqrt{1-x^2})^2$ とおく. \[ f(x) = x^4(1-x^2) = x^4-x^6\] であるから \[ f'(x) = 4x^3-6x^5 = -6x^3\left( x^2-\frac{2}{3}\right)\] であり, $f(x)$ の増減は下表のようにまとめられる ($0 < x < 1$ に注意). よって, $x = \sqrt{\dfrac{2}{3}}$ のとき, $f(x)$ は極大かつ最大の値をとる. このとき, $V$ は最大であり, 扇形の中心角の大きさは \[ 2\pi x = 2\pi\sqrt{\frac{2}{3}}\] である.

　角を通過するとき, 長さが最大の棒は, 曲がり角, 幅 $x$ の通路の壁, 幅 $y$ の通路の壁の $3$ 点で廊下に接する. このような棒のうち角を通過できるのは長さが最小のものであるから, その最小値を求めればよい. 棒が $3$ 点で廊下に接するとして, 棒と幅 $y$ の通路のなす鋭角を $\theta$ とおき, 棒の長さを $f(\theta )$ とおく. 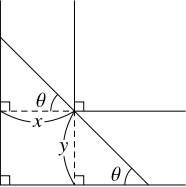棒を曲がり角で $2$ つに分けると, 棒の長さは \[ f(\theta ) = \frac{x}{\cos\theta}+\frac{y}{\sin\theta}\] と表される. \[ f'(\theta ) = \frac{x\sin\theta}{\cos ^2\theta}-\frac{y\cos\theta}{\sin ^2\theta} = \frac{x\sin ^3\theta -y\cos ^3\theta}{\sin ^2\theta\cos ^2\theta}\] であるから, \[\cos\alpha = \frac{x^{\frac{1}{3}}}{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}, \quad \sin\alpha = \frac{y^{\frac{1}{3}}}{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}\] なる鋭角 $\alpha$ について, $f(\theta )$ の増減は下表のようにまとめられる. よって, $f(\theta )$ は $\theta = \alpha$ のとき極小かつ最小の値 \[\begin{aligned} f(\alpha ) &= \frac{x}{\cos\alpha}+\frac{y}{\sin\alpha} = x\cdot\frac{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}{x^{\frac{1}{3}}}+y\cdot\frac{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}{y^{\frac{1}{3}}} \\ &= (x^{\frac{2}{3}}+y^{\frac{2}{3}})\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}} = (x^{\frac{2}{3}}+y^{\frac{2}{3}})^{\frac{3}{2}} \end{aligned}\] sをとる. ゆえに, 求める棒の長さの最大値は $(x^{\frac{2}{3}}+y^{\frac{2}{3}})^{\frac{3}{2}}$ である.

　単位円 $\mathrm O$ に内接する $\triangle\mathrm{ABC}$ について考えれば十分である. 辺 $\mathrm{BC}$ の中点を $\mathrm M$ とおき, $a = \mathrm{BM}$ とおく. さらに, $\mathrm{BC}$ を底辺としたときの高さを $h$ $(0 < h < 2)$ として, $S = \triangle\mathrm{ABC}$ とおく. 辺 $\mathrm{BC}$ を固定した場合に $h$ が最大になるとき $S$ は最大になるから, $\mathrm{AB} = \mathrm{AC}$ の場合を考えれば十分である. このとき, $\triangle\mathrm{OBM}$ は直角三角形であるから, 三平方の定理により \[\begin{aligned} a^2+|h-1|^2 &= 1^2 \\ (h-1)^2 &= 1-a^2 \\ h^2-2h+1 &= 1-a^2 \\ a^2 &= 2h-h^2 \\ a &= \sqrt{2h-h^2} \end{aligned}\] が成り立つ. よって, \[ S = \frac{1}{2}\cdot\mathrm{BC}\cdot h = ah = h\sqrt{2h-h^2}\] である. $S > 0$ により $S^2$ が最大であるとき $S$ は最大になるから, \[ S^2 = h^2(2h-h^2) = -h^4+2h^3\] の最大値を求める. \[\frac{dS^2}{dh} = -4h^3+6h^2 = -4h^2\left( h-\frac{3}{2}\right)\] であるから, $S^2$ は $h = \dfrac{3}{2}$ のとき最大値をとる. このとき, \[ a = \sqrt{2\cdot\frac{3}{2}-\left(\frac{3}{2}\right) ^2} = \frac{\sqrt 3}{2}\] であり, \[\mathrm{BC}:h = \sqrt 3:\frac{3}{2} = 2:\sqrt 3\] が成り立つから, $\triangle\mathrm{ABC}$ は正三角形である. ゆえに, $\triangle\mathrm{ABC}$ が正三角形であるとき, $S$ は最大になる.

　単位円に内接する $\triangle\mathrm{ABC}$ について考えれば十分である. $\mathrm{BC} = a,$ $\mathrm{CA} = b,$ $\angle\mathrm A = x,$ $\angle\mathrm B = y,$ $\angle\mathrm C = z,$ $S = \triangle\mathrm{ABC}$ とおく.

(1)

正弦定理により \[ a = 2\sin x, \quad b = 2\sin y\] であるから, \[\begin{aligned} S &= \frac{1}{2}ab\sin z \\ &= \frac{1}{2}\cdot 2\sin x\cdot 2\sin y\cdot\sin z \\ &= 2\sin x\sin y\sin z \end{aligned}\] が成り立つ.

(2)

(1) と $z = \pi -x-y$ から, \[\begin{aligned} S &= 2\sin x\sin y\sin (x+y) \\ &\qquad (0 < x < \pi,\ 0 < y < \pi,\ 0 < x+y < \pi) \end{aligned}\] が成り立つ. まず, $y$ を定数とみなして, \[ f(x) = 2\sin y\sin x\sin (x+y)\] の最大値を求める. \[\begin{aligned} f'(x) &= 2\sin y\{\cos x\sin (x+y)+\sin x\cos (x+y)\} \\ &= 2\sin y\sin (2x+y) \end{aligned}\] であり, $0 < y < \pi$ から $\sin y > 0$ であるので, \[\begin{aligned} f'(x) \geqq 0 &\iff \sin (2x+y) \geqq 0 \\ &\iff 2x+y \leqq \pi \iff x \leqq \frac{\pi -y}{2}, \\ f'(x) \leqq 0 &\iff x \geqq \frac{\pi -y}{2} \end{aligned}\] が成り立つ ($0 < 2x+y < 2\pi$ に注意).

$x$	$0$	$\cdots$	$\dfrac{\pi -y}{2}$	$\cdots$	$\pi$
$f'(x)$		$+$	$0$	$-$
$f(x)$		$\nearrow$	極大	$\searrow$

よって, $f(x)$ は $x = \dfrac{\pi -y}{2}$ の場合に限って, 極大かつ最大の値 \[\begin{aligned} f\left(\frac{\pi -y}{2}\right) &= 2\sin y\sin\frac{\pi +y}{2}\sin\frac{\pi -y}{2} \\ &= 2\sin y\cos ^2\frac{y}{2} = \sin y(1+\cos y) \end{aligned}\] をとる (余角公式, 半角の公式による). そこで, $x = \dfrac{\pi -y}{2}$ のもとで, この式を $g(y)$ とおき, その最大値を求める. \[\begin{aligned} g'(y) &= \cos y(1+\cos y)-\sin ^2y \\ &= 2\cos ^2y+\cos y-1 \\ &= (\cos y+1)(2\cos y-1) \end{aligned}\] であり, $0 < y < \pi$ から $\cos y+1 > 0$ であるので, \[\begin{aligned} g'(y) \geqq 0 &\iff 2\cos y-1 \geqq 0 \\ &\iff \cos y \geqq \frac{1}{2} \iff y \leqq \frac{\pi}{3}, \\ g'(y) \leqq 0 &\iff y \geqq \frac{\pi}{3}, \\ \end{aligned}\] が成り立つ.

$y$	$0$	$\cdots$	$\dfrac{\pi}{3}$	$\cdots$	$\pi$
$g'(y)$		$+$	$0$	$-$
$g(y)$		$\nearrow$	極大	$\searrow$

よって, $g(y)$ は $y = \dfrac{\pi}{3}$ の場合に限って, 極大かつ最大の値 \[\begin{aligned} g\left(\frac{\pi}{3}\right) &= \sin\frac{\pi}{3}\left( 1+\cos\frac{\pi}{3}\right) \\ &= \frac{\sqrt 3}{2}\left( 1+\frac{1}{2}\right) = \frac{3\sqrt 3}{4} \end{aligned}\] をとる. このとき, \[ x = \frac{\pi-y}{2} = \frac{\pi}{3}, \quad z = \pi -x-y = \frac{\pi}{3}\] である. ゆえに, $x = y = z = \dfrac{\pi}{3}$ のとき, $S$ は最大値 $\dfrac{3\sqrt 3}{4}$ をとる.

　四角形 $\mathrm{ABCD}$ において, $a = \mathrm{AB},$ $b = \mathrm{BC},$ $c = \mathrm{CD},$ $d = \mathrm{DA},$ $\theta = \angle\mathrm{ABC},$ $\varphi = \angle\mathrm{CDA}$ とおき, 面積を $S$ とおく. このとき, \[ S = \frac{1}{2}ab\sin\theta +\frac{1}{2}cd\sin\varphi\] が成り立つ. $S$ を $\theta$ で微分すると, \[\frac{dS}{d\theta} = \frac{1}{2}ab\cos\theta +\frac{1}{2}cd\cos\varphi\frac{d\varphi}{d\theta} \quad \cdots [1]\] となる. ここで, 余弦定理により \[\mathrm{AC}^2 = a^2+b^2-2ab\cos\theta = c^2+d^2-2cd\cos\varphi\] となるから, 両辺を $\theta$ で微分すると \[ 2ab\sin\theta = 2cd\sin\varphi\frac{d\varphi}{d\theta} \quad \cdots [2]\] となる. $[2]$ を使って $[1]$ の $\dfrac{d\varphi}{d\theta}$ を消去して整理すると, \[\frac{dS}{d\theta} = \frac{ab}{2\sin\varphi}\sin (\theta +\varphi )\] が得られる. $0 < \varphi < \pi,$ $0 < \theta +\varphi < 2\pi$ から, \[\begin{aligned} \frac{dS}{d\theta} \geqq 0 &\iff \theta +\varphi \leqq \pi, \\ \frac{dS}{d\theta} \leqq 0 &\iff \theta +\varphi \geqq \pi \end{aligned}\] が成り立つ. よって, $S$ は $\theta +\varphi = \pi$ のとき, 極大かつ最大の値をとる. ゆえに, 四角形が円に内接するとき, 四角形の面積は最大になる.

(1)

単位円に内接する $n$ 角形 $\mathrm P_1\cdots\mathrm P_n$ の周の長さ $L$ について考えれば十分である. $\mathrm P_{n+1} = \mathrm P_1$ として, $\theta _k = \angle\mathrm P_k\mathrm{OP}_{k+1}$ とおく. $\sin x$ に関する「イェンゼンの不等式」により \[\begin{aligned} L &= \sum_{k = 1}^n\mathrm P_k\mathrm P_{k+1} = \sum_{k = 1}^n2\sin\frac{\theta _k}{2} = 2n\sum_{k = 1}^n\frac{1}{n}\sin\frac{\theta _k}{2} \\ &\leqq 2n\sin\left(\sum_{k = 1}^n\frac{1}{n}\cdot\frac{\theta _k}{2}\right) = 2n\sin\frac{\pi}{n} \end{aligned}\] であり, 等号成立は $\dfrac{\theta _1}{2} = \cdots = \dfrac{\theta _n}{2}$ の場合に限るから, 単位円に内接する $n$ 角形のうち周の長さ $L$ が最大になるものは正 $n$ 角形である.

(2)

$\sin x$ に関する「イェンゼンの不等式」を示す.

(i)

$n = 2$ のとき. $x_2$ を定数とみなして, $0 < x_1 < \pi$ の範囲で $x_1$ の関数 \[ f(x_1) = \sin (t_1x_1+t_2x_2)-t_1\sin x_1-t_2\sin x_2\] を考える. \[ f'(x_1) = t_1\{\cos (t_1x_1+t_2x_2)-\cos x_1\}\] であり, $\cos x$ $(0 < x < \pi )$ は単調減少であるから, $t_1x_1+t_2x_2 \leqq x_1$ つまり $x_1 \geqq x_2$ のとき $f'(x_1) \geqq 0$ であり, $t_1x_1+t_2x_2 \geqq x_1$ つまり $x_1 \leqq x_2$ のとき $f'(x_1) \leqq 0$ である. よって, $f(x_1) \geqq f(x_2) = 0$ であるから, \[\sin (t_1x_1+t_2x_2) \geqq t_1\sin x_1+t_2\sin x_2 \quad (0 < x_1 < \pi )\] が成り立ち, 等号成立は $x_1 = x_2$ の場合に限る.

(ii)

$n = m$ ($m$: $2$ 以上の整数) のとき不等式と等号成立条件が成り立つとする. $n = m+1$ の場合に, $s = t_1+\cdots +t_m$ とおく. \[ u_k = \frac{t_k}{s} \quad (1 \leqq k \leqq m)\] とおくと, \[\begin{aligned} &\sin\left(\sum_{k = 1}^{m+1}t_kx_k\right) \\ &= \sin\left(\sum_{k = 1}^mt_kx_k+t_{m+1}x_{m+1}\right) \\ &= \sin\left( s\sum_{k = 1}^mu_kx_k+t_{m+1}x_{m+1}\right) \\ &\geqq s\sin\left(\sum_{k = 1}^mu_kx_k\right) +t_{m+1}\sin x_{m+1} \quad (\because\text{(i)}) \\ &\geqq s\sum_{k = 1}^mu_k\sin x_k+t_{m+1}\sin x_{m+1} \\ &= \sum_{k = 1}^{m+1}t_k\sin x_k \end{aligned}\] が得られる. 等号成立は, “ $\displaystyle\sum\limits_{k = 1}^mu_kx_k = x_{m+1},$ $x_1 = \cdots = x_m$ ” つまり $x_1 = \cdots = x_m = x_{m+1}$ の場合に限る.

(i), (ii) から, $2$ 以上のすべての整数 $n$ に対して不等式, 等号成立条件が成り立つ.

　$1$ 辺の長さが $1$ の正方形 $\mathrm{ABCD}$ の形をした紙を考える. その対角線の交点を $\mathrm O,$ 辺 $\mathrm{AB}$ の中点を $\mathrm M$ とおく. 対称性により, $\mathrm O$ を通り $\mathrm{AM}$ と共有点をもつ直線 $l$ で折る場合について考えれば十分である. $l$ と $\mathrm{AB}$ の交点を $\mathrm E$ とおき, $l$ に関して $\mathrm A,$ $\mathrm D$ と対称な点を $\mathrm A',$ $\mathrm D'$ とおく. 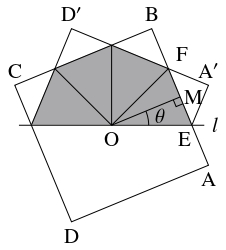さらに, $\theta = \angle\mathrm{MOE}$ とおいて, 紙が重なった部分の面積を $S$ とおく. このとき, $0 \leqq \theta \leqq \dfrac{\pi}{4}$ となる. $0 < \theta \leqq \dfrac{\pi}{4}$ のとき, $\mathrm{AB},$ $\mathrm A'\mathrm D'$ の交点を $\mathrm F$ とおくと, 対称性と \[\begin{aligned} \mathrm{OE} &= \frac{\mathrm{OM}}{\cos\theta} = \frac{1}{2\cos\theta}\ \left(\because\mathrm{OM} = \dfrac{1}{2}\right), \\ \mathrm{OF} &= \frac{\mathrm{OM}}{\cos\left(\dfrac{\pi}{4}-\theta\right)} = \frac{1}{2\cos\left(\dfrac{\pi}{4}-\theta\right)} \end{aligned}\] であることから, \[\begin{aligned} S &= 4\triangle\mathrm{OEF} = 4\cdot\frac{1}{2}\mathrm{OE}\cdot\mathrm{OF}\sin\frac{\pi}{4}\ \left(\because\angle\mathrm{EOF} = \frac{\pi}{4}\right) \\ &= \frac{1}{2\sqrt 2\cos\theta\cos\left(\dfrac{\pi}{4}-\theta\right)} \quad \cdots [1] \end{aligned}\] が得られる. これは $\theta = 0$ のときにも成り立つ. $0 \leqq \theta \leqq \dfrac{\pi}{4}$ として, 積和の公式により $[1]$ を変形すると, \[\begin{aligned} S &= \frac{1}{\sqrt 2\left\{\cos\dfrac{\pi}{4}+\cos\left( 2\theta -\dfrac{\pi}{4}\right)\right\}} \\ &= \frac{1}{1+\sqrt 2\cos\left( 2\theta -\dfrac{\pi}{4}\right)} \end{aligned}\] が得られる. ゆえに, $S$ は $2\theta -\dfrac{\pi}{4} = 0$ つまり $\theta = \dfrac{\pi}{8}$ のとき最小値 $\dfrac{1}{1+\sqrt 2} = \sqrt 2-1$ をとるから, 求める割合は \[ (\sqrt 2-1)\div 1 = \sqrt 2-1\] である.