本格数学クイズ (積分法)
面積
クイズ《棒の通過範囲の面積》
鉛直な壁に垂直に立てかけられた細い棒が水平な床に, 上端が壁に接したまま下端が床をすべりながら倒れた.
このときの棒の通過範囲の面積は, 下端を中心に回転して倒れたときの何倍か.
(有名問題)
答え
$\dfrac{3}{8}$ 倍.
解説
床を $x$ 軸 $(x \geqq 0)$, 壁を $y$ 軸 ($y \geqq 0$), 棒を長さ $1$ の線分として考える.
上端が壁に接したまま下端が床をすべりながら倒れたときの棒の通過範囲は $x$ 軸, $y$ 軸に接する長さ $1$ の線分の通過範囲に等しく,
下端を中心に回転して倒れたときの棒の通過範囲は半径 $1$ の四分円である.
- (1)
- まず, 線分の通過範囲を表す式を求める.
点 $(x,y)$ $(0 < x < 1,$ $0 < y < 1)$ が線分の通過範囲にあることは,
\[ y = \sin\theta -x\tan\theta\]
を満たす鋭角 $\theta$ の存在と同値である.
ここで,
\[\frac{dy}{d\theta} = \cos\theta -\frac{x}{\cos ^2\theta} = \frac{\cos ^3\theta -x}{\cos ^2\theta}\]
であるから, $\cos ^3\alpha = x$ なる鋭角 $\alpha$ について, $y$ の増減は下表のようにまとめられる.
また, \[\cos\alpha = x^{\frac{1}{3}}, \quad \sin\alpha = (1-x^{\frac{2}{3}})^{\frac{1}{2}}\] であるから, $y$ は $\theta = \alpha$ のとき極大かつ最大の値 \[\begin{aligned} \sin\alpha -x\tan\alpha &= (1-x^{\frac{2}{3}})^{\frac{1}{2}}-x\cdot\frac{(1-x^{\frac{2}{3}})^{\frac{1}{2}}}{x^{\frac{1}{3}}} \\ &= (1-x^{\frac{2}{3}})(1-x^{\frac{2}{3}})^{\frac{1}{2}} \\ &= (1-x^{\frac{2}{3}})^{\frac{3}{2}} \end{aligned}\] をとる. よって, 線分の通過範囲は, \[ y \leqq (1-x^{\frac{2}{3}})^{\frac{3}{2}}, \quad x \geqq 0, \quad y \geqq 0\] つまり \[ x^{\frac{2}{3}}+y^{\frac{2}{3}} \leqq 1, \quad x \geqq 0, \quad y \geqq 0\] と表される.
$\theta$ $0$ $\cdots$ $\alpha$ $\cdots$ $\dfrac{\pi}{2}$ $\dfrac{dy}{d\theta}$ $+$ $0$ $-$ $y$ $\nearrow$ 極大 $\searrow$ 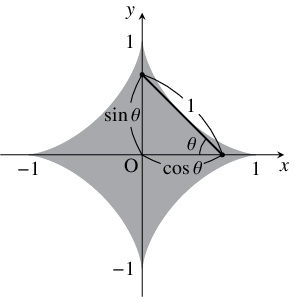
- (2)
- 線分の通過範囲の面積を求め, 面積比を求める. (1) の領域は, 曲線 \[ x = \cos ^3\theta, \quad y = \sin ^3\theta \quad \left( 0 \leqq \theta \leqq \frac{\pi}{2}\right)\] と $x$ 軸, $y$ 軸で囲まれた部分に等しい. $\theta$ が $0$ から $\dfrac{\pi}{2}$ まで増加するとき, $x$ は $1$ から $0$ まで単調に減少する. $\dfrac{dx}{d\theta} = -3\cos ^2\theta\sin\theta$ であるから, 求める面積は \[\begin{aligned} \int_0^1y\,dx &= \int_{\frac{\pi}{2}}^0y\dfrac{dx}{d\theta}\,d\theta \\ &= \int_{\frac{\pi}{2}}^0\sin ^3\theta (-3\cos ^2\theta\sin\theta )\,d\theta \\ &= 3\int_0^{\frac{\pi}{2}}\sin ^4\theta\cos ^2\theta\,d\theta \\ &= 3\int_0^{\frac{\pi}{2}}\sin ^4\theta (1-\sin ^2\theta )\,d\theta \\ &= 3\int_0^{\frac{\pi}{2}}(\sin ^4\theta -\sin ^6\theta )\,d\theta \\ &= 3\left(\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2}-\frac{5}{6}\cdot\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2}\right) \\ &= \frac{3}{32}\pi \end{aligned}\] である. よって, 求める面積比は, \[\frac{3}{32}\pi\div\frac{\pi}{4} = \frac{3}{8}\] である.
クイズ《円の周りを回転する円上の動点の軌跡》
円 $C$ は半径が同じ定円 $O$ の周りをすべることなく回転している.
$C$ 上の点 $\mathrm P$ が $O$ と接したときから再び $O$ と接するまで動くとき, $\mathrm P$ の軌跡が囲む領域の面積は $C$ の面積の何倍か.
(有名問題)
答え
$6$ 倍.
解説
- (1)
- 原点 $\mathrm O$ を中心とする半径 $a$ の円に, 点 $\mathrm C$ を中心とする半径 $b$ の円が, 接しながらすべることなく転がるとする.
$\overrightarrow{\mathrm{OP}} = \overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{CP}}$ である.
円 $\mathrm O$ と円 $\mathrm C$ の接点を $\mathrm T$ とおき, 線分 $\mathrm{CP}$ の線分 $\mathrm{CT}$ からの回転角を $\varphi$ とおく.
このとき, 弧 $\mathrm{AT}$ と弧 $\mathrm{TP}$ の長さは等しいから,
が成り立つ.
$a\theta = b\varphi$ つまり $\varphi = \dfrac{a}{b}\theta$ - (i)
- 円 $\mathrm O$ に円 $\mathrm C$ が外接するとき.
$\overrightarrow{\mathrm{OC}} = (a+b)(\cos\theta,\sin\theta )$ である.
また, 線分 $\mathrm{CP}$ の $x$ 軸の正方向からの回転角は
\[\theta +\pi +\varphi = \theta +\pi +\dfrac{a}{b}\theta = \pi +\dfrac{a+b}{b}\theta\]
であるから,
\[\overrightarrow{\mathrm{CP}} = -b\left(\cos\frac{a+b}{b}\theta ,\sin\frac{a+b}{b}\theta\right)\]
が成り立つ.
よって,
\[\begin{aligned}
x &= (a+b)\cos\theta -b\cos\frac{a+b}{b}\theta, \\
y &= (a+b)\sin\theta -b\sin\frac{a+b}{b}\theta
\end{aligned}\]
である.
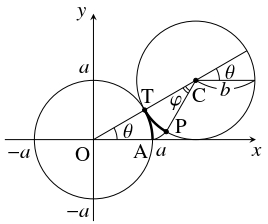
- (2)
- (1) において $a = b = \dfrac{1}{2}$ とすると, 点 $\mathrm P$ の軌跡 (「カージオイド」と呼ばれる曲線になる) の媒介変数表示
\[\begin{aligned}
x &= \cos\theta -\frac{1}{2}\cos 2\theta \\
&= \cos\theta -\frac{1}{2}(2\cos ^2\theta -1) \\
&= \frac{1}{2}+(1-\cos\theta )\cos\theta, \\
y &= \sin\theta -\frac{1}{2}\sin 2\theta \\
&= \sin\theta -\sin\theta\cos\theta \\
&= (1-\cos\theta )\sin\theta
\end{aligned}\]
が得られる.
この曲線が囲む領域の面積 $S$ と半径 $\dfrac{1}{2}$ の円の面積の比を求めればよい.
$x$ 軸方向に $-\dfrac{1}{2}$ だけ平行移動して $y$ 軸に関して対称移動した曲線の媒介変数表示
\[\begin{cases}
x = -(1-\cos\theta )\cos\theta, \\
y = (1-\cos\theta )\sin\theta
\end{cases}\]
において $\theta$ を $\pi -\theta$ に置き換えることにより,「カージオイド」の有名な媒介変数表示
\[\begin{cases}
x = (1+\cos\theta )\cos\theta, \\
y = (1+\cos\theta )\sin\theta
\end{cases}\]
が得られる.
ここで,
\[\begin{aligned}
\{ 1+\cos (-\theta )\}\cos (-\theta ) &= (1+\cos\theta )\cos\theta \\
\{ 1+\cos (-\theta )\}\sin (-\theta ) &= -(1+\cos\theta )\sin\theta
\end{aligned}\]
であるから, 曲線の $-\pi \leqq \theta \leqq 0$ の部分と $0 \leqq \theta \leqq \pi$ の部分は $x$ 軸に関して対称である.
\[\begin{aligned}
\frac{dx}{d\theta} &= -\sin\theta\cos\theta +(1+\cos\theta )(-\sin\theta ) \\
&= -\sin\theta (1+2\cos\theta )
\end{aligned}\]
であるから,
$\theta$ が $0$ から $\dfrac{2}{3}\pi$ まで増加するとき $x$ は $2$ から $-\dfrac{1}{4}$ まで単調に減少し,
$\theta$ が $\dfrac{2}{3}\pi$ から $\pi$ まで増加するとき $x$ は $-\dfrac{1}{4}$ から $0$ まで単調に増加する.
$0 \leqq \theta \leqq \dfrac{2}{3}\pi$ の部分の $y$ 座標を $y_1,$
$\dfrac{2}{3}\pi \leqq \theta \leqq \pi$ の部分の $y$ 座標を $y_2$ とおくと,
\[\begin{aligned}
&S = 2\left(\int_{-\frac{1}{4}}^2y_1\,dx-\int_{-\frac{1}{4}}^0y_2\,dx\right) \\
&= 2\left[\int_{\frac{2}{3}\pi}^0(1+\cos\theta )\sin\theta\{ -\sin\theta (1+2\cos\theta )\}\,d\theta\right. \\
&\qquad \left.\int_{\frac{2}{3}\pi}^\pi (1+\cos\theta )\sin\theta\{ -\sin\theta (1+2\cos\theta )\}\,d\theta\right] \\
&= 2\int_0^\pi\sin ^2\theta (1+\cos\theta )(1+2\cos\theta )\,d\theta \\
&= 2\int_0^\pi (-2\cos ^4\theta -3\cos ^3\theta +\cos ^2\theta +3\cos\theta +1)\,d\theta \\
&= 2\!\int_0^\pi\!\left(-\frac{\cos 4\theta}{4}\!-\!\frac{3\cos 3\theta}{4}\!-\!\frac{\cos 2\theta}{2}\!+\!\frac{3\cos\theta}{4}\!+\!\frac{3}{4}\right)d\theta \\
&= 2\left[ -\frac{\sin 4\theta}{16}-\frac{\sin 3\theta}{4}-\frac{\sin 2\theta}{4}+\frac{3\sin\theta}{4}+\frac{3\theta}{4}\right] _0^\pi \\
&= \frac{3}{2}\pi
\end{aligned}\]
が得られる.
ゆえに, 動点 $\mathrm P$ の軌跡が囲む領域の面積は円 $C$ の面積の
である.$S\div\left(\dfrac{1}{2}\right) ^2\pi = \dfrac{3}{2}\pi\div\dfrac{1}{4}\pi = 6$ (倍)
クイズ《ヤギの問題》
平らな農場で, ヤギが円柱形の柱の一端に伸び縮みのしないひもでつながれている.
ひもの長さが柱の周の長さに等しいとき, ヤギが動き回れる範囲の面積は, 柱の断面積の何倍か.
ただし, ヤギの大きさ, ひもの太さとつなぎ目は考えないものとする.
(有名問題)
答え
$\dfrac{5}{6}\pi ^2$ 倍.
解説
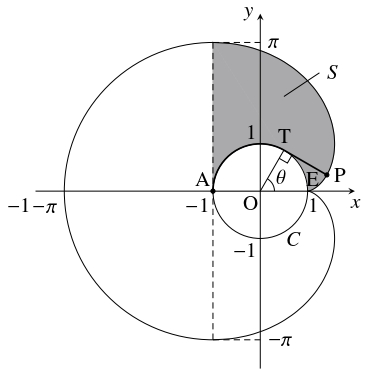
ひもの固定端を通る水平面が $xy$ 平面, 柱の断面が単位円となるように座標軸を定め, 固定端を点 $\mathrm A(-1,0)$ とする.
はじめ, 長さ $\pi$ のひもが円周 $C:x^2+y^2 = 1$ 上に時計回りにたるみなく巻きつけられているとする.
ヤギがひもをたるみなくほどいていくとき, ヤギの動点を $\mathrm P,$ ひものほどいた部分と $C$ の接点を $\mathrm T$ とおき, $\mathrm O(0,0),$ $\mathrm E(1,0)$ として $\theta = \angle\mathrm{EOT}$ $(0 \leqq \theta \leqq \pi )$ とおく.
- (1)
- まず, 点 $\mathrm P$ が描く曲線の媒介変数表示を求める.
$\overrightarrow{\mathrm{TP}}$ は $\overrightarrow{\mathrm{OT}} = (\cos\theta,\sin\theta )$ の単位法線ベクトルの $1$ つ $\vec n = (\sin\theta,-\cos\theta )$ を $\stackrel{\frown}{\mathrm{ET}} = \theta$ 倍に伸ばしたベクトルであるから,
$\overrightarrow{\mathrm{OP}}$ は
\[\begin{aligned}
\overrightarrow{\mathrm{OP}} &= \overrightarrow{\mathrm{OT}}+\overrightarrow{\mathrm{TP}} = \overrightarrow{\mathrm{OT}}+\theta\vec n \\
&= (\cos\theta,\sin\theta )+\theta (\sin\theta,-\cos\theta ) \\
&= (\cos\theta +\theta\sin\theta,\sin\theta -\theta\cos\theta )
\end{aligned}\]
と表される.
よって, 点 $\mathrm P$ が描く曲線は,
\[\begin{aligned}
x &= \cos\theta +\theta\sin\theta, \\
y &= \sin\theta -\theta\cos\theta
\end{aligned}\]
と表される.
- (2)
- ヤギが動き回れる範囲の面積を求め, 柱の断面積との比を求める. 点 $\mathrm A$ より左側では, ヤギは中心 $\mathrm A,$ 半径 $\pi$ の半円の上を動き回れる. 点 $\mathrm A$ より右側でヤギが動き回れる範囲は $x$ 軸に関して対称であるから, その $x$ 軸より上側の部分の面積を $S$ とおく. それは $0 \leqq \theta \leqq \pi$ におけるひもの先端 $\mathrm P\,(\neq \mathrm A)$ の軌跡と $x$ 軸, 直線 $x = -1$ が囲む図形から円の上半分を除いた部分の面積に等しい. 点 $\mathrm P(x,y)$ について (1) から \[\frac{dy}{d\theta}= \cos\theta -\cos\theta +\theta\sin\theta = \theta\sin\theta\] であるので, \[\begin{aligned} &S+\frac{\pi}{2} = \int_0^\pi\{ x-(-1)\}\,dy \\ &= \int_0^\pi (1+x)\frac{dy}{d\theta}\,d\theta \\ &= \int_0^\pi (1+\cos\theta +\theta\sin\theta )\theta\sin\theta\,d\theta \\ &= \int_0^\pi (\theta\sin\theta +\theta\sin\theta\cos\theta +\theta ^2\sin ^2\theta )\,d\theta \\ &= \int_0^\pi\left(\theta\sin\theta +\theta\cdot\frac{\sin 2\theta}{2}+\theta ^2\cdot\frac{1-\cos 2\theta}{2}\right)\,d\theta \\ &= \int_0^\pi\theta\sin\theta\,d\theta +\frac{1}{2}\int_0^\pi\theta\sin 2\theta\,d\theta \\ &\qquad +\frac{1}{2}\int_0^\pi\theta ^2\,d\theta -\frac{1}{2}\int_0^\pi\theta ^2\cos 2\theta\,d\theta \\ &= [\theta (-\cos\theta )]_0^\pi -\int_0^\pi (-\cos\theta )\,d\theta \\ &\qquad +\frac{1}{2}\left[\theta\cdot\frac{-\cos 2\theta}{2}\right] _0^\pi -\frac{1}{2}\int_0^\pi\frac{-\cos 2\theta}{2}\,d\theta \\ &\qquad +\frac{1}{2}\left[\frac{\theta ^3}{3}\right] _0^\pi -\frac{1}{2}\left[\theta ^2\cdot\frac{\sin 2\theta}{2}\right] _0^\pi +\frac{1}{2}\int_0^\pi 2\theta\cdot\frac{\sin 2\theta}{2}\,d\theta \\ &= \pi +[\sin\theta ]_0^\pi -\frac{\pi}{4}+\frac{1}{4}\left[\frac{\sin 2\theta}{2}\right] _0^\pi +\frac{\pi ^3}{6}+\frac{1}{2}\int_0^\pi\theta\sin 2\theta\,d\theta \\ &= \pi-\frac{\pi}{4}+\frac{\pi ^3}{6}-\frac{\pi}{4} \\ &= \frac{\pi ^3}{6}+\frac{\pi}{2} \end{aligned}\] から \[ S = \frac{\pi ^3}{6}\] が得られる. ゆえに, ヤギが動き回れる範囲の面積は, \[\frac{\pi ^3}{2}+2S = \frac{\pi ^3}{2}+2\cdot\frac{\pi ^3}{6} = \frac{5}{6}\pi ^3\] であり, 柱の断面積の \[\frac{5}{6}\pi ^3\div (\pi\cdot 1^2) = \frac{5}{6}\pi ^2\] 倍である.
体積
クイズ《パイプの共通部分の体積》
前後, 左右, 上下方向に延びる内径の等しいパイプの軸が $1$ 点で直交するとき, $3$ 本のパイプの共通部分の体積は, パイプが円柱状である場合, 正四角柱である場合の何倍になるか.
(有名問題)
答え
$2-\sqrt 2$ 倍 ($0.58578\cdots$ 倍).
解説
- (1)
- 内径が $2$ である直交する $3$ 本の正四角柱の共通部分の体積 $W$ は \[ W = 2^3 = 8\] である.
- (2)
- 内径が $2$ である直交する $3$ 本の円柱
\[ y^2+z^2 \leqq 1, \quad z^2+x^2 \leqq 1,\quad x^2+y^2 \leqq 1\]
の共通部分の体積 $V$ を求める.
共通部分は, 中央の立方体の部分と, その面に接する $6$ つの合同な部分からなる.
立方体の部分について, 面の対角線の長さは円柱の直径 $2$ に等しいから, $1$ 辺の長さは $\sqrt 2$ である.
また, $6$ つの合同な部分のうち, $\dfrac{1}{\sqrt 2} \leqq z \leqq 1$ における部分について, 平面 $z = t$ による切り口の面積は図のように長方形
になるから, 平面 $z = t$ による円柱の共通部分の切り口は正方形 \[\left\{\begin{array}{l} |x| \leqq \sqrt{1-t^2}, \\ |y| \leqq \sqrt{1-t^2} \end{array}\right.\] になる.$\left\{\begin{array}{l} |x| \leqq 1, \\ |y| \leqq \sqrt{1-t^2} \end{array}\right.$ と $\left\{\begin{array}{l} |y| \leqq 1, \\ |x| \leqq \sqrt{1-t^2} \end{array}\right.$ この面積は \[ S(t) = (2\sqrt{1-t^2})^2 = 4(1-t^2)\] であるから, 求める体積は \[\begin{aligned} V &= (\sqrt 2)^3+6\int_{\frac{1}{\sqrt 2}}^1S(t),dt \\ &= 2\sqrt 2+24\int_{\frac{1}{\sqrt 2}}^1(1-t^2)\,dt \\ &= 2\sqrt 2+24\left[ t-\frac{t^3}{3}\right] _{\frac{1}{\sqrt 2}}^1 \\ &= 16-8\sqrt 2 \end{aligned}\] である.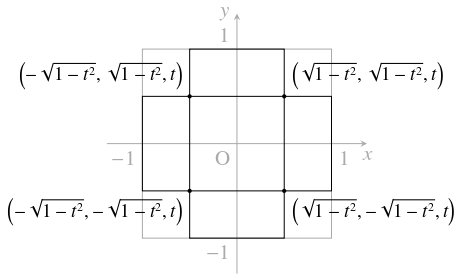
- (3)
- ゆえに, 求める体積比は \[\frac{V}{W} = \frac{16-8\sqrt 2}{8} = 2-\sqrt 2\] である.
参考
- 複数の円柱の共通部分として定まる立体を「シュタインメッツの立体」(Steinmetz solid) と呼ぶ.
- 底面の半径が $1$ であって軸が四面体の頂点と重心を通る $4$ 本の円柱の共通部分の体積は $12\sqrt 2(2-\sqrt 3)$ であることが知られている.
- 底面の半径が $1$ であって軸が立方体の面の対角線に平行で重心を通る $6$ 本の円柱の共通部分の体積は $\dfrac{16}{3}(3+2\sqrt 3-4\sqrt 2)$ であることが知られている.
長さ
クイズ《タイヤの周上の点が動く長さ》
タイヤの周上の $1$ 点はタイヤが $1$ 回転する間にタイヤの半径の何倍の長さを動くか.
(有名問題)
答え
$8$ 倍.
解説
タイヤの半径を $1$ とする.
周期性により, タイヤの周上の点としてはじめに道路と接地している点を考えればよい.
このような点が描く軌跡は, 進行方向を $x$ 軸, 進行方向に対して垂直上方向を $y$ 軸, 回転角を $\theta$ とすると,
\[ x = \theta -\sin\theta, \quad y = 1-\cos\theta\]
で表される (こちらを参照).
$x = \theta -\sin\theta,$ $y = 1-\cos\theta$ を $\theta$ で微分すると
\[\frac{dx}{d\theta} = 1-\cos\theta, \quad \frac{dy}{d\theta} = \sin\theta\]
となるから
\[\begin{aligned}
\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2 &= (1-\cos\theta )^2+\sin ^2\theta \\
&= 1-2\cos\theta +\cos ^2\theta +\sin ^2\theta \\
&= 2-2\cos\theta = 4\sin ^2\frac{\theta}{2} \\
\end{aligned}\]
であり, $0 \leqq \theta \leqq 2\pi$ において $\sin\dfrac{\theta}{2} \geqq 0$ である.
よって, タイヤが $1$ 回転するとき, 上記の点の軌跡の長さは
\[\begin{aligned}
&\int_0^{2\pi}\sqrt{\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2 }\,d\theta \\
&= \int_0^{2\pi}\sqrt{4\sin ^2\frac{\theta}{2}}\,d\theta \\
&= 2\int_0^{2\pi}\sin\frac{\theta}{2}\,d\theta \\
&= 2\left[ -2\cos\frac{\theta}{2}\right] _0^{2\pi} \\
&= 2\cdot (-2)(-1-1) = 8
\end{aligned}\]
である.
ゆえに, タイヤの周上の $1$ 点はタイヤの半径の
の長さを動く.
| $8\div 1 = 8$ (倍) |
クイズ《円の伸開線の長さ》
円に伸び縮みのしないひもをたるみなく巻きつけていくと, ちょうど $1$ 周したところで巻き終わった.
このとき, ひもの先端が描く曲線の長さはひもの長さの何倍か.
ただし, ひもの太さは無視して考えるものとする.
(有名問題)
答え
$\pi$ 倍.
解説
伸び縮みのしない長さ $2\pi$ のひもの一端を原点 $\mathrm O(0,0)$ に固定し, 他端 $\mathrm P$ が点 $\mathrm A(2\pi,0)$ 上にある状態から, ひもを円周 $C:x^2+(y-1)^2 = 1$ 上に反時計回りにたるみなく巻きつける.
- (1)
- まず, 点 $\mathrm P$ が描く曲線の媒介変数表示を求める.
円周 $C$ の中心を $\mathrm B$ とおき, $C$ 上の点 $\mathrm Q$ までひもを巻きつけたとき, $\theta = \angle\mathrm{OBQ}$ とおく.
$\angle\mathrm{OBQ} = \theta$ のとき $\mathrm Q(\sin\theta,1-\cos\theta )$ であるから,
\[\begin{aligned}
\overrightarrow{\mathrm{BQ}} &= \overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OB}} \\
&= (\sin\theta,1-\cos\theta )-(0,1) \\
&= (\sin\theta,-\cos\theta )
\end{aligned}\]
であり, この単位法線ベクトルは
\[\pm (\cos\theta,\sin\theta )\]
である.
$\overrightarrow{\mathrm{QP}}$ は $\vec n = (\cos\theta,\sin\theta )$ を $\mathrm{PQ} = \mathrm{OA}-\stackrel{\frown}{\mathrm{OQ}} = 2\pi -\theta$ 倍に伸ばしたベクトルであるから,
\[\begin{aligned}
&\overrightarrow{\mathrm{OP}} = \overrightarrow{\mathrm{OQ}}+\overrightarrow{\mathrm{QP}} \\
&= \overrightarrow{\mathrm{OQ}}+(2\pi -\theta )\vec n \\
&= (\sin\theta,1-\cos\theta )+(2\pi -\theta )(\cos\theta,\sin\theta ) \\
&= (\sin\theta+(2\pi -\theta )\cos\theta,1-\cos\theta +(2\pi -\theta )\sin\theta )
\end{aligned}\]
である.
よって, 点 $\mathrm P$ が描く曲線は,
\[\begin{aligned}
x &= \sin\theta+(2\pi -\theta )\cos\theta, \\
y &= 1-\cos\theta +(2\pi -\theta )\sin\theta
\end{aligned}\]
と表される.
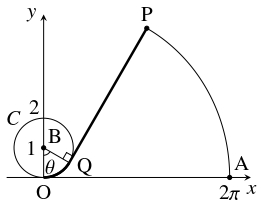
- (2)
- (1) の曲線について \[\begin{aligned} \frac{dx}{d\theta} &= \cos\theta -\cos\theta +(2\pi -\theta )(-\sin\theta ) \\ &= -(2\pi -\theta )\sin\theta, \\ \frac{dy}{d\theta} &= \sin\theta -\sin\theta +(2\pi -\theta )\cos\theta \\ &= (2\pi -\theta )\cos\theta \end{aligned}\] であるから, 点 $\mathrm P$ が描く曲線の長さは \[\begin{aligned} \int _0^{2\pi}\sqrt{\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2}\,d\theta &= \int _0^{2\pi}(2\pi -\theta )\,d\theta \\ &= \left[ 2\pi\theta -\frac{\theta ^2}{2}\right] _0^{2\pi} \\ &= 2\pi ^2 \end{aligned}\] であり, これはひもの長さの \[ 2\pi ^2\div 2\pi = \pi\] 倍である.
参考
伸び縮みのしないひもをある図形にたるみなく巻きつけていくとき, またはそれをたるみなくほどいていくとき, ひもの先端が描く軌跡はその図形の「伸開線」または「インボリュート」(involute) と呼ばれる.
クイズ《放物線の長さ》
動点が放物線 $y = \dfrac{x^2}{4p}$ $(p \neq 0)$ 上の $0 \leqq x \leqq b$ の範囲を動くとき, どれだけの道のりを動くか.
(有名問題)
答え
$\dfrac{1}{4|p|}\left( b\sqrt{b^2+4p^2}+4p^2\log\dfrac{b+\sqrt{b^2+4p^2}}{2|p|}\right).$
解説
求める道のりを $L$ とおく.
- (1)
- $y = \dfrac{x^2}{4p}$ を微分すると, \[\frac{dy}{dx} = \frac{2x}{4p} = \frac{x}{2p}\] となる. よって, 曲線の長さの公式により, \[\begin{aligned} L &= \int_0^b\sqrt{1+\left(\frac{dy}{dx}\right) ^2}\,dx \\ &= \int_0^b\sqrt{1+\left(\frac{x}{2p}\right) ^2}\,dx \\ &= \frac{1}{2|p|}\int_0^b\sqrt{x^2+4p^2}\,dx \end{aligned}\] である.
- (2)
- 不定積分 $\displaystyle\int\sqrt{x^2+a^2}\,dx$ $(a = 2p)$ を求める. \[\begin{aligned} &\int\sqrt{x^2+a^2}\,dx = \int (x)'\sqrt{x^2+a^2}\,dx \\ &= x\sqrt{x^2+a^2}-\int x\cdot\frac{2x}{2\sqrt{x^2+a^2}}\,dx \\ &= x\sqrt{x^2+a^2}-\int\frac{(x^2+a^2)-a^2}{\sqrt{x^2+a^2}}\,dx \\ &= x\sqrt{x^2+a^2}-\int\sqrt{x^2+a^2}\,dx+a^2\int\frac{dx}{\sqrt{x^2+a^2}} \end{aligned}\] であり, $t = x+\sqrt{x^2+a^2}$ とおくと \[\frac{dt}{dx} = 1+\frac{2x}{2\sqrt{x^2+a^2}} = \frac{t}{\sqrt{x^2+a^2}}\] よって \[\frac{1}{\sqrt{x^2+a^2}}\cdot\frac{dx}{dt} = \frac{1}{t}\] となり, したがって \[\begin{aligned} &\int\frac{dx}{\sqrt{x^2+a^2}} = \int\frac{dt}{t} \\ &= \log t+C = \log (x+\sqrt{x^2+a^2})+C \end{aligned}\] ($C$: 積分定数) であることから, \[\begin{aligned} &\int\sqrt{x^2+a^2}\,dx \\ &= \frac{1}{2}\left( x\sqrt{x^2+a^2}+a^2\int\frac{dx}{\sqrt{x^2+a^2}}\right) \\ &= \frac{1}{2}\left\{ x\sqrt{x^2+a^2}+a^2\log (x+\sqrt{x^2+a^2})\right\} +C \end{aligned}\] ($C$: 積分定数) である.
- (3)
- (1), (2) により, 求める道のりは, \[\begin{aligned} &L = \frac{1}{2|p|}\cdot\frac{1}{2}\left[ x\sqrt{x^2+4p^2}+4p^2\log (x+\sqrt{x^2+4p^2})\right] _0^b \\ &= \frac{1}{4|p|}\{ b\sqrt{b^2+4p^2}+4p^2\log (b+\sqrt{b^2+4p^2})-4p^2\log 2|p|\} \\ &= \frac{1}{4|p|}\left( b\sqrt{b^2+4p^2}+4p^2\log\frac{b+\sqrt{b^2+4p^2}}{2|p|}\right) \end{aligned}\] である.
微分方程式
クイズ《バクテリアの増殖》
あるバクテリアの増殖率はその時点の数に比例するという.
このバクテリアが $n$ 倍に増殖するまでにかかる時間と, $n$ 倍から $n^2$ 倍に増殖するまでにかかる時間はどちらが長いか.
(有名問題, 参考: 東海大)
答え
同じ.
解説
バクテリアの数を $x\,(> 0)$ で表し, 増殖率の比例定数を $k$ とおく.
- (1)
-
このとき, 仮定により
が成り立つ. 両辺を $t$ で積分すると,$\dfrac{dx}{dt} = kx$ つまり $\dfrac{1}{x}\dfrac{dx}{dt} = k$
が得られる. (なお, $x = e^{kt+C} = e^Ce^{kt}$ により, $x = ce^{kt}$ $(c = e^C)$ が得られる.)$\log x = kt+C$ ($C$: 積分定数) - (2)
- バクテリアの数 $x$ が時刻 $t = t_1$ から $t = t_2$ までに $n$ 倍になるとすると, \[\begin{aligned} \log x &= kt_1+C \quad \cdots [1], \\ \log nx &= kt_2+C \quad \cdots [2] \end{aligned}\] となるから, $([2]-[1])\div k$ により \[ t_2-t_1 = \frac{\log nx-\log x}{k} = \frac{(\log n+\log x)-\log x}{k} = \frac{\log n}{k}\] が得られる. よって, このバクテリアが $n$ 倍に増殖するまでにかかる時間は最初の数によらず一定である.