本格数学クイズ (整数論)
初等整数論
クイズ《素数の無限性》
素数が無限に存在することを複数の方法で示せ.
(有名問題, 参考: $1973$ 大阪歯科大)
答え
解説を参照.
解説 1 (ユークリッド, 紀元前 $3$ 世紀頃)
$p_1,$ $\cdots,$ $p_r$ を素数として,
\[ q = p_1\cdots p_r+1\,(> 1)\]
とおく.
- (i)
- $q$ が素数であるとき. $q$ は $p_1,$ $\cdots,$ $p_r$ と異なる素数の例を与える.
- (ii)
- $q$ が合成数であるとき. $q$ は, $p_1,$ $\cdots,$ $p_r$ と互いに素であるから, $p_1,$ $\cdots,$ $p_r$ と異なる素因数をもつ.
解説 2: 階乗を利用
$p$ を素数として,
\[ q = p!+1\,(> 1)\]
とおく.
- (i)
- $q$ が素数であるとき. $q$ は $p$ より大きい素数の例を与える.
- (ii)
- $q$ が合成数であるとき. $q$ は, $1,$ $\cdots,$ $p$ と互いに素であるから, $p$ より大きい素因数をもつ.
解説 3:「シルヴェスター数列」を利用
こちらを参照.
解説 4:「フェルマー数」の数列を利用 (ゴールドバッハ, $1730$ 年)
こちらを参照.
解説 5 (サイダック, $2006$ 年)
$a$ を $1$ より大きい整数として,
\[ a_1 = a, \quad a_{n+1} = a_n(a_n+1)\]
で数列 $\{ a_n\}$ を定める.
このとき, $a_1$ は少なくとも $1$ つの素因数をもつ.
また, $a_n+1$ は, $a_n$ と互いに素であるから $a_n$ と異なる素因数をもち, $a_{n+1}$ は $a_n$ より多くの素因数をもつ.
$\{ a_n\}$ において各項の素因数の個数は単調に増加するので, 素数は無限に存在する.
クイズ《完全数》
$p,$ $q$ を素数とする.
$p\times q$ マスの余白のない方眼紙を罫線に沿って $1$ 個以上の合同な小長方形に分ける.
このような分け方すべてにわたる小長方形の個数の総和がマス目の個数の $2$ 倍に等しいとき, $pq$ の値はいくらか.
(オリジナル)
答え
$6.$
解説
$p \leqq q$ としても一般性を失わない.
$p,$ $q$ は素数であるから, $1\times 1$ の長方形 $pq$ 個, $1\times q$ の長方形 $p$ 個, $p\times 1$ の長方形 $q$ 個, $p\times q$ の長方形 $1$ 個に分ける方法がある.
これらの長方形の個数の総和がマス目の個数 $pq$ の $2$ 倍に等しいとき,
\[\begin{aligned}
pq+p+q+1 &= 2pq \\
pq-p-q+1 &= 2 \\
(p-1)(q-1) &= 2
\end{aligned}\]
が成り立つ.
$2 \leqq p \leqq q$ から $1 \leqq p-1 \leqq q-1$ であるので,
\[\begin{aligned}
(p-1,q-1) &= (1,2) \\
(p,q) &= (2,3)
\end{aligned}\]
である.
ゆえに, 求める値は $pq = 6$ である.
参考
- 正の整数 $a$ の正の約数の総和 $\sigma (a)$ が $2a$ になるとき, つまり $a$ のそれ自身を除く正の約数の総和が $a$ になるとき, $a$ を「完全数」(perfect number) と呼ぶ.
- 偶数の「完全数」は $2^p-1$ が素数であるような素数 $p$ を用いて $2^{p-1}(2^p-1)$ と表される (こちらを参照).
- 奇数の「完全数」は発見されていない.
- 「完全数」が無限に存在するかどうかは未解決である.
- 上記のクイズに関して, 一般に, 隣り合う $2$ 辺の長さが互いに素な整数 $m,$ $n$ である長方形の $1$ 個以上の合同な「整数長方形」のタイルへの分割すべてにわたるタイル数の総和が最大のタイル数 $mn$ の $2$ 倍に等しいとき, $mn$ は「完全数」になる.
ここで, 辺の長さが整数である長方形を「整数長方形」と呼び, 分割でできたタイルは「内部」が合同であるとき合同であるという.
実際, タイル数の総和は $m$ の正の約数 $d,$ $n$ の正の約数 $e$ すべてにわたる $\dfrac{m}{d}\cdot\dfrac{n}{e}$ の総和に等しく, これは $de$ の総和に等しい. 分配法則により, これは $\sigma (m)\sigma (n)$ に等しいから, \[\sigma (m)\sigma (n) = 2mn \quad \cdots [\ast ]\] が成り立つ. $m,$ $n$ が互いに素であれば, $\sigma (m)\sigma (n) = \sigma (mn)$ が成り立つから, $[\ast ]$ は \[\sigma (mn) = 2mn\] つまり $mn$ が「完全数」であることを意味する.
クイズ《カルキン=ウィルフ木》
$\dfrac{1}{1}$ から始めて, 既存の各分数に対して,
①分子はそのままで, もとの分母ともとの分子の和を分母として, 新たな分数を作る,
②分母はそのままで, もとの分母ともとの分子の和を分子として, 新たな分数を作る,
という $2$ つの操作を延々と繰り返す.
このとき, 作られる分数の中に現れない正の有理数は存在するか.
存在する場合にはその例を挙げ, 存在しない場合にはそのことを証明せよ.
(ヒント: 逆の操作を考えてみよ.)
(有名問題, 参考: $2019$ 大阪大)
答え
存在しない (証明は解説を参照).
解説
- (1)
- $\dfrac{a}{1}$ ($a$: 正の整数) の形の分数も既約分数とみなすとき, 各操作でできる分数は既約分数であることに注意する. 実際, $\dfrac{1}{1}$ は既約分数であり, 既約分数 $\dfrac{a}{b}$ ($a,$ $b$: 互いに素な正の整数) に対して, $a+b$ と $a$ も, $a+b$ と $b$ も互いに素であるから, ①, ②の操作で作られる分数も既約分数である.
- (2)
- ①, ②の操作で作られた分数 $\dfrac{a}{b}$ ($a,$ $b$: 互いに素な正の整数) に対して, もとの分数は, $a > b$ のとき $\dfrac{a-b}{b},$ $a < b$ のとき $\dfrac{a}{b-a}$ である.
- (3)
- $c = \dfrac{a}{b}$ ($a,$ $b$: 互いに素な正の整数) を任意の正の有理数とする.
$a = b$ のとき, $c = \dfrac{1}{1}$ である.
$a \neq b$ のとき, この分数から始めて, (2) のいずれかの分数を作るという操作 (逆操作と呼ぶ) を繰り返すことで分数 $\dfrac{1}{1}$ が作られることを示せばよい.
- (i)
- $a > b$ のとき. $a$ を $b$ で割った商を $q,$ 余りを $r$ とすると, $c$ から $q$ 回の逆操作で分数 $c' = \dfrac{r}{b}$ が作られる. $r \neq 1$ であれば, $b$ を $r$ で割った商を $q',$ 余りを $r'$ とすると, $c'$ から $q'$ 回の逆操作で分数 $c'' = \dfrac{r}{r'}$ が作られる. これを繰り返すと, $a,$ $b$ が互いに素であるという仮定とユークリッドの互除法により, 分母または分子は $1$ になる. 分母, 分子の一方が $1,$ 他方が $s$ の分数からは, $s-1$ 回の逆操作で分数 $\dfrac{1}{1}$ が作られる.
- (ii)
- $a < b$ のとき. (i) と同様に, 逆操作を繰り返すことで分数 $\dfrac{1}{1}$ が作られる.
クイズ《有理数の単位分数の和への分解》
$0$ より大きく $1$ より小さいすべての有理数は, 有限個の相異なる正の整数の逆数の和として表すことができるか.
可能な場合には証明を述べ, 不可能な場合には反例を挙げよ.
(ヒント: 分母を分子で割った商が $q$ であるとき, $q+1$ の逆数を $1$ つの項として考えてみよ.)
(有名問題, 参考: $2021$ 広島大)
答え
できる (証明は解説を参照).
解説
有理数 $\dfrac{a}{b}$ ($a,$ $b$: 互いに素な整数, $0 < a < b$) が
の形に表されることを示す.
| $\dfrac{a}{b} = \dfrac{1}{d_1}+\cdots +\dfrac{1}{d_n}$ ($d_k$: 整数, $1 < d_1 < \cdots < d_n$) $\cdots [\ast ]$ |
- (1)
- $b$ を $a$ で割った商が $q,$ 余りが $r$ であるとき, \[\begin{aligned} &\frac{a}{b} = \frac{1}{q+1}+\frac{a-r}{b(q+1)} \quad \cdots [1], \\ &0 < a-r < a \end{aligned}\] が成り立つことに注意する.
- (2)
- $a = 1$ のとき, $d_1 = b$ とおけばよい. $a \geqq 2$ のとき, $\dfrac{a}{b}$ を $[1]$ のように表し, $d_1 = q+1$ とおく. $a-r = 1$ のとき, $q+1 < b(q+1)$ に注意して, $d_2 = b(q+1)$ とおけばよい. $a-r \geqq 2$ のとき, 同様の議論により, $\dfrac{a-r}{b(q+1)}$ は $d_1$ より大きい整数 $d_2$ の逆数と分子がより小さい分数 (分母, 分子は正) の和として表せる. $a$ 以下の正の整数は $a$ 個しかないから, この操作を高々 $a$ 回繰り返すと, 残りの分数の分子も $1$ になり, 求める表示 $[\ast ]$ が得られる.
参考
古代エジプトでは, 整数でない有理数を表すとき, $\dfrac{2}{3}$ を唯一の例外として, 相異なる「単位分数」(分子が $1$ の分数) の和として表した.
このように表された有理数を「エジプト分数」と呼ぶ.
「エジプト分数」は, 中世までヨーロッパで広く使われていた.
不定方程式
クイズ《フロベニウスの硬貨交換問題》
$a,$ $b$ を互いに素な $1$ より大きい整数とする.
$a$ 円硬貨, $b$ 円硬貨のみを使ってちょうど支払えない金額は最大で何円か.
ただし, 各硬貨は何枚使ってもよいが, おつりはもらえないものとする.
(有名問題)
答え
$ab-a-b$ 円.
解説
$c$ 円が $a$ 円硬貨, $b$ 円硬貨のみを使って支払えるとき,
\[ ax+by = c \quad \cdots [\ast ]\]
は非負の整数解をもつ.
よって, $[\ast ]$ が非負の整数解をもたないような正の整数 $c$ の最大値を求めればよい.
例えば, $a,$ $b$ $(a < b)$ が $1$ 桁の素数であるとき, そのような $c$ の値は,
\[ c = \begin{cases}
1 & (a = 2,\ b = 3), \\
3 & (a = 2,\ b = 5), \\
5 & (a = 2,\ b = 7), \\
7 & (a = 3,\ b = 5), \\
11 & (a = 3,\ b = 7), \\
23 & (a = 5,\ b = 7)
\end{cases}\]
である.
これらの数値から求める金額は $ab-a-b$ 円であると推測できるので, そのことを証明する.
- (1)
- $c = ab-a-b$ のとき $[\ast ]$ は非負の整数解をもたないことを示す. 整数 $x,$ $y$ が \[ ax+by = ab-a-b \quad \cdots [1]\] つまり \[ a(x+1)+b(y+1) = ab \quad \cdots [2]\] を満たすとする. \[ a(x+1) = b(a-y-1), \quad a(b-x-1) = b(y+1)\] であり, $a,$ $b$ は互いに素であるから, $x+1$ は $b$ の倍数, $y+1$ は $a$ の倍数である. $[2]$ の左辺が $ab$ を超える $ab$ の倍数になることはないから, $x,$ $y \geqq 0$ となることはない. ゆえに, $[1]$ は非負の整数解をもたない.
- (2)
- $c \geqq ab-a-b+1$ のとき, $[\ast ]$ は非負の整数解をもつことを示す. $a,$ $b$ は互いに素であるから, \[ ax+by = c \quad \cdots [3]\] は整数解 $(x,y) = (x_0,y_0)$ をもつ. $x_0$ を $b$ で割った商 $q$ について $(x,y) = (x_0-bq,y_0+aq)$ も $[3]$ の整数解であるから, $0 \leqq x \leqq b-1$ なる整数解が存在する. このような $[3]$ の整数解 $(x,y)$ について, \[ y = \frac{c-ax}{b} \geqq \frac{ab-a-b+1-a(b-1)}{b} = \frac{1}{b}-1 > -1\] であるから, $y \geqq 0$ も成り立つ. ゆえに, $[3]$ は非負の整数解をもつ.
参考
$a_1,$ $\cdots,$ $a_n$ を互いに素な正の整数とする.
- $a_1$ 円硬貨 (切手), $\cdots,$ $a_n$ 円硬貨 (切手) のみを使ってちょうど支払えない金額 (郵便料金) の最大値を求める問題を「フロベニウスの硬貨交換問題」(coin-exchange problem of Frobenius) または「シルヴェスターの切手問題」(Sylvester's postage stamp problem) と呼び, その最大値を整数の組 $\{ a_1,\cdots,a_n\}$ の「フロベニウス数」(Frobenius number) と呼ぶ.
- $n \geqq 3$ のとき,「フロベニウス数」を求める明示的な公式は発見されていない. $n = 3$ のとき,「フロベニウス数」の上限, 下限が得られており,「フロベニウス数」を求める高速なアルゴリズムも発見されている.
- $a_1$ 円硬貨 (切手), $a_2$ 円硬貨 (切手) のみを使ってちょうど支払えない金額 (郵便料金) は $\dfrac{(a_1-1)(a_2-1)}{2}$ 通りであることが, シルヴェスターによって示されている.
クイズ《底面積と側面積が等しい整数三角柱》
高さが $1$ であり, 残りの辺の長さも整数であって, 底面積と側面積が等しい三角柱は何個あるか.
(有名問題, 脚色あり)
答え
$5$ 個.
解説
このような三角柱において, 底面の $3$ 辺の長さを $a,$ $b,$ $c$ $(a \leqq b \leqq c)$ とし, $s = \dfrac{a+b+c}{2}$ とおく.
底面積は「ヘロンの公式」により $\sqrt{s(s-a)(s-b)(s-c)},$ 側面積は $(a+b+c)\cdot 1 = 2s$ であるから,
\[\sqrt{s(s-a)(s-b)(s-c)} = 2s\]
が成り立つ.
両辺を $2$ 乗して $s$ で割ると
\[ (s-a)(s-b)(s-c) = 4s \quad \cdots [1]\]
が得られる.
\[ x = s-a, \quad y = s-b, \quad z = s-c \quad \cdots [2]\]
とおく.
このとき,
\[ x+y+z = 3s-(a+b+c) = 3s-2s = s \quad \cdots [3]\]
であるから, $[2]$ のもとで $[1]$ は
\[ xyz = 4(x+y+z)\]
つまり
\[ x = \frac{4(y+z)}{yz-4}\]
と同値である ($(yz-4)x = 4(y+z) > 0$ から $yz-4 > 0$ であることに注意).
\[ x \geqq y \geqq z > 0\]
であり, よって
\[ x \leqq \frac{4(y+y)}{z\cdot z-4} = \frac{8y}{z^2-4}\]
が成り立つから, 仮に $z \geqq 4$ であるとすると
\[ x \leqq \frac{8y}{4^2-4} = \frac{2}{3}y\]
となってしまい $x \geqq y$ であることに反する.
よって, $1 \leqq z \leqq 3$ である.
- (i)
- $z = 1$ のとき. \[ x = \frac{4(y+1)}{y-4} = \frac{4(y-4)+20}{y-4} = 4+\frac{20}{y-4}\] であるから, $y-4$ は $20$ の約数である. $y \geqq 0$ に注意すると \[\begin{aligned} y-4 &= -2,\ -1,\ 1,\ 2,\ 4,\ 5,\ 10,\ 20 \\ y &= 2,\ 3,\ 5,\ 6,\ 8,\ 9,\ 14,\ 24 \end{aligned}\] となるから, $x \geqq y$ に注意すると \[ (x,y) = (24,5),\ (14,6),\ (9,8)\] が得られる.
- (ii)
- $z = 2$ のとき. \[ x = \frac{4(y+2)}{2y-4} = \frac{2(y+2)}{y-2} = \frac{2(y-2)+8}{y-2} = 2+\frac{8}{y-2}\] であるから, $y-2$ は $8$ の約数である. $y \geqq 0$ に注意すると \[\begin{aligned} y-2 &= -1,\ 1,\ 2,\ 4,\ 8 \\ y &= 1,\ 3,\ 4,\ 6,\ 10 \end{aligned}\] となるから, $x \geqq y$ に注意すると \[ (x,y) = (10,3),\ (6,4)\] が得られる.
- (iii)
- $z = 3$ のとき. $y \geqq 3$ かつ \[ x = \frac{4(y+3)}{3y-4} = \frac{\dfrac{4}{3}(3y-4)+\dfrac{52}{3}}{3y-4} = \frac{4}{3}+\frac{52}{3(3y-4)}\] である. $y = 3$ のとき, 右辺は $\dfrac{4}{3}+\dfrac{52}{3(3\cdot 3-4)} = \dfrac{24}{5}$ となるから, 等式は成り立たない. 仮に $y \geqq 4$ であるとすると \[ x \leqq \frac{4}{3}+\frac{52}{3(3\cdot 4-4)} = \frac{21}{6} < 4\] となってしまい, $x \geqq y$ であることに反する. よって, 等式は成り立たない.
参考
周の長さと面積が等しい図形を「等長積図形」と呼ぶ (equable shape の和訳として提案したい).
クイズ《底面積と側面積が等しい整数直方体》
高さが整数 $z$ であり, 残りの辺の長さも整数であって, 底面積と側面積が等しい直方体は何個あるか.
(オリジナル)
答え
$z$ が $z = 2^{e_0}p_1{}^{e_1}\cdots p_r{}^{e_r}$ ($e_0$: 非負整数, $p_k$: 相異なる $3$ 以上の素数, $e_r$: 正の整数) と素因数分解されるとき,
| $\dfrac{(2e_0+3)(2e_1+1)\cdots (2e_r+1)+1}{2}$ 個. |
解説
このような直方体において, 横の長さを $x,$ 縦の長さを $y$ とおく.
底面積は $xy,$ 側面積は $2xz+2yz$ であるから,
\[ xy = 2xz+2yz\]
が成り立つ.
この方程式は
\[\begin{aligned}
xy-2xz-2yz+4z^2 &= 4z^2 \\
(x-2z)(y-2z) &= 4z^2
\end{aligned}\]
と変形できる.
よって, 整数の組 $(x-2z,y-2z)$ は $4z^2$ の正の約数と $1$ 対 $1$ に対応する.
したがって, 整数の組 $(x,y)$ も $4z^2$ の正の約数と $1$ 対 $1$ に対応する.
$4z^2$ は平方数であるから, その正の約数の個数 $N$ は奇数であり, $x = y = 4z$ のときに限り $x,$ $y$ の値は一致する.
また, 横の長さと縦の長さを入れ替えた直方体も同じ直方体であるから, 条件を満たす直方体の個数は
である.
ここで, $z$ が
と素因数分解されるとき,
\[ 4z^2 = 2^{e_0+2}p_1{}^{2e_1}\cdots p_r{}^{2e_r}\]
であり, 約数の和の公式により
\[ N = (2e_0+3)(2e_1+1)\cdots (2e_r+1)\]
であるから, 求める個数は
である.
| $\dfrac{N-1}{2}+1 = \dfrac{N+1}{2}$ (個) |
| $z = 2^{e_0}p_1{}^{e_1}\cdots p_r{}^{e_r}$ |
| ($e_0$: 非負整数, $p_k$: 相異なる $3$ 以上の素数, $e_r$: 正の整数) |
| $\dfrac{(2e_0+3)(2e_1+1)\cdots (2e_r+1)+1}{2}$ 個 |
参考
- $z = 1$ のとき, 上記のような直方体は $2$ 個ある.
- 周の長さと面積が等しい図形を「等長積図形」と呼ぶ (equable shape の和訳として提案したい). $z = 1$ のときの直方体の底面は「等長積長方形」である.
クイズ《ピタゴラスの $3$ つ組に現れる整数》
同じ長さのマッチ棒をつなげて直角三角形の枠を作るとき, $1$ 辺に使われるマッチ棒の本数として考えられない整数の最大値はいくらか.
(オリジナル)
答え
$2.$
解説
各辺のマッチ棒の本数を $a,$ $b,$ $c$ とおく.
三平方の定理により
\[ a^2+b^2 = c^2 \quad (a,\ b,\ c > 0) \quad \cdots [\ast ]\]
が成り立つ.
- (i)
- まず, $a = 2$ または $b = 2$ または $c = 2$ であるとき, $[\ast ]$ が成り立たないことを示す. \[ (c+b)(c-b) = c^2-b^2 = 2^2 \quad (b,\ c \geqq 0)\] の整数解は $c+b = c-b = 2$ から $(b,c) = (0,2)$ に限るので ($c+b = 4,$ $c-b = 1$ なら $c = \dfrac{5}{2}$ となってしまう), $a = 2$ のとき $[\ast ]$ は成り立たない. 同様に, $b = 2$ のときも $[\ast ]$ は成り立たない. また, \[ a^2+b^2 = 2^2 \quad (a,\ b \geqq 0)\] の整数解は $a,$ $b \in \{ 0,1,2\}$ から $(a,b) = (2,0),\ (0,2)$ に限るので, $c = 2$ のとき $[\ast ]$ は成り立たない.
- (ii)
- $a$ が奇数で $a \geqq 3$ であるとき. $a^2$ は $9$ 以上の奇数で $a^2\pm 1$ は正の偶数, よって $\dfrac{a^2\pm 1}{2}$ は正の整数であり, \[\begin{aligned} &\left(\frac{a^2+1}{2}\right) ^2-\left(\frac{a^2-1}{2}\right) ^2 \\ &= \frac{(a^4+2a^2+1)-(a^4-2a^2+1)}{4} = \frac{4a^2}{4} = a^2 \end{aligned}\] から \[ a^2+\left(\frac{a^2-1}{2}\right) ^2 = \left(\frac{a^2+1}{2}\right) ^2\] が成り立つので, $b = \dfrac{a^2-1}{2},$ $c = \dfrac{a^2+1}{2}$ とおけば $[\ast ]$ を満たす整数 $b,$ $c$ が得られる.
- (iii)
- $a$ が $4$ の倍数であるとき.
$a$ は $a = 2^ea'$ ($e$: $2$ 以上の整数, $a'$: 正の奇数) と表せる.
- $a' = 1$ のとき, \[ 4^2+3^2 = 5^2\] であるから, $b = 2^{e-2}\cdot 3,$ $c = 2^{e-2}\cdot 5$ とおけば $[\ast ]$ を満たす整数 $b,$ $c$ が得られる.
- $a' \geqq 3$ のとき. (ii) により \[ a'^2+b'^2 = c'^2\] を満たす正の整数 $b',$ $c'$ が存在する. よって, $b = 2^eb',$ $c = 2^ec'$ とおけば $[\ast ]$ を満たす整数 $b,$ $c$ が得られる.
- (iv)
- $a$ を $4$ で割った余りが $2$ で $a \geqq 6$ であるとき. $a' = \dfrac{a}{2}$ は $3$ 以上の奇数であるから, (ii) により \[ a'^2+b'^2 = c'^2\] を満たす正の整数 $b',$ $c'$ が存在する. よって, $b = 2b',$ $c = 2c'$ とおけば $[\ast ]$ を満たす整数 $b,$ $c$ が得られる.
クイズ《辺長が整数である格子三角形の面積》
方眼紙の罫線 (間隔は $1$) の交点を頂点とする三角形において, 各辺の長さが整数であるならば面積も整数である, という主張は正しいか.
正しければ証明し, 正しくなければ反例を挙げよ.
(オリジナル)
答え
正しい (証明は解説を参照).
解説
方眼紙の罫線の交点を頂点とする三角形 $T$ において, $3$ 辺の長さ $a,$ $b,$ $c$ ($a < c,$ $b < c$) が整数であるとする.
- (i)
- $T$ の $2$ 辺が方眼の罫線上にあるとき. $T$ は各辺の長さが整数の直角三角形である (このような三角形を「ピタゴラスの三角形」と呼ぶ). ここで, 直角を挟む $2$ 辺の長さ $a,$ $b$ の少なくとも一方は偶数である. 実際, 三平方の定理により \[ a^2+b^2 = c^2\] が成り立ち, 偶数 $2n$ の $2$ 乗 $4n^2$ を $4$ で割った余りは $0,$ 奇数 $2n+1$ の $2$ 乗 $4n(n+1)+1$ を $4$ で割った余りは $1$ であるから, $a$ も $b$ も奇数であるとすると $c^2$ を $4$ で割った余りは $2$ になって $c$ は偶数にも奇数にもならないという矛盾が起こるからである. よって, $T$ の面積 $\dfrac{ab}{2}$ は整数である.
- (ii)
- $T$ の $2$ 辺が方眼の罫線上にないとき. $T$ は, $4$ 辺が方眼の罫線上にある長方形の $2$ つまたは $3$ つの角 (かど) から「ピタゴラスの三角形」を取り除いて得られる. 長方形の面積は整数であり, (i) により取り除く三角形の面積も整数であるから, $T$ の面積も整数である.
参考
- $xy$ 平面上の $x$ 座標, $y$ 座標が整数である点を「格子点」(lattice point) と呼び, 各頂点が格子点であるような多角形を「格子多角形」(lattice polygon) と呼ぶ.
- $3$ 辺の長さが整数である三角形を「整数三角形」(integer triangle) と呼び, $3$ 辺の長さと面積が整数である三角形を「ヘロンの三角形」(Heronian triangle) と呼ぶ.
- 本問で示したことにより,「整数三角形」のうち,「格子三角形」である三角形は「ヘロンの三角形」である. 逆に,「ヘロンの三角形」は「格子三角形」として描けることが知られている.
クイズ《平方三角数》
正方形 (中実方陣) の形に並べられた複数個の石を, $1$ 段目に $1$ 個, $\cdots,$ $k$ 段目に $k$ 個, $\cdots$ と並べ直していくと, 正三角形の形に余すことなく並べられた.
このとき, 考えられる石の個数として最も少ない個数は何個か.
(有名問題)
答え
$36$ 個.
解説
複数個の石が $l$ 行 $l$ 列の正方形の形にも, $m$ 段の正三角形の形にも並べられたとする.
このとき, $l,$ $m \geqq 2$ と
が成り立つ.
$[1]$ の右辺の $m$ に $2$ 以上の整数を代入していくと, 初めて平方数になる値は $m = 8$ のときの
\[\frac{8\cdot 9}{2} = 36\]
である.
よって, 考えられる石の個数として最も少ない個数は $36$ 個である.
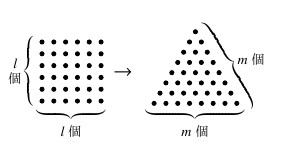

参考
- 正三角形の形に点を並べたときの点の総数を「三角数」と呼び, 平方数でも「三角数」でもある整数を「平方三角数」と呼ぶ.
- 「平方三角数」$l^2 = \dfrac{m(m+1)}{2}$ と「ペル方程式」$x^2-2y^2 = 1$ の正の整数解 $(x,y)$ は \[ (x,y) = (2m+1,2l)\] により $1$ 対 $1$ に対応している (こちらを参照). このことと $x^2-2y^2 = 1$ の解の公式 (こちらを参照) を合わせると, 小さい方から $n$ 番目の「平方三角数」は, \[\frac{\{ (1+\sqrt 2)^{2n}-(1-\sqrt 2)^{2n}\} ^2}{32}\] と表せることがわかる (L・オイラー, $1778$ 年). 小さい順に「平方三角数」を列記すると, $1,$ $36,$ $1225,$ $41616,$ $1413721,$ $\cdots$ となる.
クイズ《出席番号の和》
複数人の生徒からなるクラスの全員が出席番号順に $1$ 列に並んでいる.
列の先頭と最後尾からそれぞれ生徒の出席番号の和をとっていったとき, 出席番号が奇数である生徒で $2$ つの和が等しくなった.
この生徒の出席番号として考えられる値は最小でいくらか.
(有名問題)
答え
$35$ 番.
解説
生徒が $m$ 人 $(m \geqq 2)$ いるとして, 出席番号が $l$ 番 $(l \geqq 2)$ の生徒で $2$ つの和が等しくなったとする.
このとき,
\[\begin{aligned}
\sum_{k = 1}^lk &= \sum_{k = 1}^mk-\sum_{k = 1}^{l-1}k \\
\frac{l(l+1)}{2} &= \frac{m(m+1)}{2}-\frac{l(l-1)}{2} \\
l^2 &= \frac{m(m+1)}{2} \quad \cdots [1]
\end{aligned}\]
が成り立つ.
ここで, $l$ が奇数であるとすると, $m$ を $4$ で割った余りは $1$ または $2$ になる.
$[1]$ の右辺の $m$ にこのような $2$ 以上の整数を代入していくと, 初めて奇数の平方数になる値は $m = 49$ のときの
\[\frac{49\cdot 50}{2} = 35^2 = 1225\]
である.
よって, 生徒の出席番号として考えられる番号の最小値は $35$ である (このときクラスの人数は $49$ 人).
参考
出席番号順に並んだ生徒の列の先頭と最後尾からそれぞれ生徒の出席番号の和をとっていったとき, ある生徒で $2$ つの和が等しくなったとする.
- この生徒の出席番号として考えられる値の $2$ 乗は前問の「平方三角数」である.
- この生徒の出席番号として考えられる $n$ 番目に小さい値は $2n$ 番目の「ペル数」(Pell number) $y_{2n}$ を $2$ で割った値であり, \[\frac{y_{2n}}{2} = \frac{(1+\sqrt 2)^{2n}-(1-\sqrt 2)^{2n}}{4\sqrt 2}\] である. $y_{2n}$ は $y$ の値が $n$ 番目に小さい $x^2-2y^2 = 1$ の正の整数解の $y$ 成分である. なお, $2n-1$ 番目の「ペル数」$y_{2n-1}$ は $y$ の値が $n$ 番目に小さい $x^2-2y^2 = -1$ の正の整数解の $y$ 成分である.
クイズ《辺長が等差数列をなすヘロンの三角形》
$1$ 辺の長さが $1$ のマッチ棒をつなげて, 鋭角三角形の枠を作る.
各辺で使う本数が等差数列になり, 面積が整数になるようにするとき, 考えられるマッチ棒の本数として最も少ない本数は何本か.
(オリジナル)
答え
$42$ 本.
解説
三角形の $3$ 辺の長さ (マッチ棒の本数) を $a = b-z,$ $b,$ $c = b+z$ $(0 < z < b),$ 面積を $S$ とおく.
このとき, ヘロンの公式により,
\[\begin{aligned}
S &= \sqrt{\frac{3b}{2}\left(\frac{3b}{2}-b+z\right)\left(\frac{3b}{2}-b\right)\left(\frac{3b}{2}-b-z\right)} \\
&= \frac{\sqrt{3b(b+2z)b(b-2z)}}{4} \\
&= \frac{b\sqrt{3(b^2-4z^2)}}{4}
\end{aligned}\]
が成り立つ.
$b$ が奇数であるとすると, $b^2-4z^2$ も奇数になり, 右辺の分子は奇数になってしまい, $S$ が整数であることに反する.
よって, $b$ は偶数である. そこで, $x = \dfrac{b}{2}$ とおくと, \[ S = \frac{2x\sqrt{3(4x^2-4z^2)}}{4} = x\sqrt{3(x^2-z^2)}\] となる. これが整数であるとき, ある正の整数 $y$ に対して \[ x^2-z^2 = 3y^2\] つまり \[ x^2-3y^2 = z^2 \quad \cdots [\ast ]\] となる.
である.
$b$ が奇数であるとすると, $b^2-4z^2$ も奇数になり, 右辺の分子は奇数になってしまい, $S$ が整数であることに反する.
よって, $b$ は偶数である. そこで, $x = \dfrac{b}{2}$ とおくと, \[ S = \frac{2x\sqrt{3(4x^2-4z^2)}}{4} = x\sqrt{3(x^2-z^2)}\] となる. これが整数であるとき, ある正の整数 $y$ に対して \[ x^2-z^2 = 3y^2\] つまり \[ x^2-3y^2 = z^2 \quad \cdots [\ast ]\] となる.
- (I)
- $z = 1$ のとき. $[\ast ]$ の正の整数解のうち $x$ の値が最小のもの, $2$ 番目に小さいものは \[ (x,y) = (2,1),\ (7,4)\] であり, これらに対応する $3$ 辺の長さは \[ (a,b,c) = (3,4,5),\ (13,14,15)\] である. 前者は直角三角形をなし, 後者は鋭角三角形をなす.
- (II)
- $z \geqq 2$ のとき.
- (i)
- $2 \leqq z \leqq 12$ のとき. $[\ast ]$ は $(x,y) = (7,4)$ より $x$ の値が小さい正の整数解をもたないことが, 数値実験から確認できる. ちなみに, $2 \leqq z \leqq 10,$ $z = 12$ のとき $[\ast ]$ の整数解は $z = 1$ の場合の解の倍数であり (証明は省略), $z = 11$ のとき $[\ast ]$ の正の整数解のうち $x$ の値が最小のものは $(x,y) = (14,5)$ である.
- (ii)
- $z \geqq 13$ のとき. \[ x = \sqrt{z^2+3y^2} > z\] である.
| $13+14+15 = 42$ (本) |
クイズ《有理点の距離》
$xy$ 平面において $x$ 座標も $y$ 座標も有理数である点を有理点と呼ぶ.
$2$ つの有理点の間の距離が $1,$ $\sqrt 2$ となることはある.
それでは, $2$ つの有理点の間の距離が $\sqrt 3$ となることはあるか.
(有名問題)
答え
ない (理由は以下の通り).
解説
平行移動により $1$ 点は原点であるとしてよい.
もう $1$ 点の座標を $(x,y)$ とすると, $2$ 点間の距離は $\sqrt{x^2+y^2}$ となるから, $\sqrt{x^2+y^2} = \sqrt 3$ つまり
\[ x^2+y^2 = 3\]
が有理数解をもたないことを示せばよい.
$x = \dfrac{a}{c},$ $y = \dfrac{b}{c}$ ($a,$ $b,$ $c$: 整数, $c > 0$) のとき,
\[ x^2+y^2 = 3 \iff a^2+b^2 = 3c^2\ \cdots [1]\]
であるから, $[1]$ の整数解が存在しても $a,$ $b,$ $c$ は互いに素でないことを示す.
- (i)
- $a,$ $b$ の少なくとも一方が $3$ の倍数のとき. $a$ が $3$ の倍数であるとしてよい. このとき, $b^2 = 3c^2-a^2$ は $3$ の倍数であるから, $b$ は $3$ の倍数である. よって, $3c^2 = a^2+b^2$ は $9$ の倍数であるから, $c^2$ は $3$ の倍数で, $c$ は $3$ の倍数である. したがって, $[1]$ の整数解は互いに素でない.
- (ii)
- $a = 3d\pm 1,$ $b = 3e\pm 1$ ($d,$ $e$: 整数, 複号任意) のとき. \[\begin{aligned} a^2+b^2 &= (3d\pm 1)^2+(3e\pm 1)^2 \\ &= 3(3d^2+3e^2\pm 2d\pm 2e)+2 \end{aligned}\] (かっこ内は整数) は $3$ で割り切れない. よって, $[1]$ の整数解は存在しない.
クイズ《平方四角錐数》
正方形 (中実方陣) の形に並べられた複数個の球を, $1$ 段目に $1$ 個, $\cdots,$ $k$ 段目に $k$ 個, $\cdots$ となるように積み上げていくと, 正四角錐の形に余すことなく並べられた.
このとき, 考えられる球の個数として最も少ない個数は何個か.
(参考:『新しいカギ』「第 $1$ 回高校生クイズ何問目」決勝 $2$ 問目)
答え
$4900$ 個.
解説
複数個の球が $x$ 段の正四角錐の形にも, $y$ 行 $y$ 列の正方形の形にも並べられたとする.
このとき,
が成り立つ.
| $y^2 = \displaystyle\sum_{k = 1}^xk^2$ つまり $y^2= \dfrac{1}{6}x(x+1)(2x+1) \quad \cdots [*]$ |
- (1)
- $x,$ $x+1,$ $2x+1$ はどの $2$ つも互いに素であることに注意する. 実際, $x+1,$ $2x+1$ を $x$ で割った余りは $1$ であるから, $x$ と $x+1,$ $x$ と $2x+1$ は互いに素である. また, $-(2x+1) = -2(x+1)+1$ を $x+1$ で割った余りは $1$ であるから, $x+1$ と $-(2x+1)$ は互いに素であり, よって $x+1$ と $2x+1$ は互いに素である.
- (2)
- $5$ 以上の各素数 $p$ に対して, $x,$ $x+1,$ $2x+1$ が $p$ で割り切れる回数はいずれも偶数 ($0$ を含む) であることに注意する. 実際, $[*]$ は \[ 6y^2 = x(x+1)(2x+1)\] と同値である. $5$ 以上の各素数 $p$ に対して, $6y^2$ つまり $x(x+1)(2x+1)$ が $p$ で割り切れる回数は偶数であり, (1) の注意から $x,$ $x+1,$ $2x+1$ のうち高々 $1$ つしか $p$ で割り切れないので, $x,$ $x+1,$ $2x+1$ が $p$ で割り切れる回数はいずれも偶数である.
- (3)
- 最後に, $[*]$ の $(x,y) = (1,1)$ 以外の正の整数解のうち $x$ の値が最小のものを求め, 球の個数を求める.
$(x,y)$ を $[*]$ の正の整数解とする.
(2) の注意から, $x,$ $x+1,$ $2x+1$ が $5$ 以上の素数で割り切れる回数が奇数になることはない.
- $x = 5,$ $7,$ $10,$ $11,$ $13,$ $14,$ $15,$ $17,$ $19,$ $20,$ $21,$ $22,$ $23$ は, $x$ が $5$ 以上の素数で割り切れる回数が奇数になることがあるから, 不適.
- $x = 4,$ $6,$ $9,$ $12,$ $16,$ $18$ は, それぞれ $x+1 = 5,$ $7,$ $10,$ $13,$ $17,$ $19$ が $5$ 以上の素数で割り切れる回数が奇数になることがあるから, 不適.
- $x = 2,$ $3,$ $8$ は, それぞれ $2x+1 = 5,$ $7,$ $17$ が $5$ 以上の素数であるから, 不適.
- $\dfrac{1}{6}\cdot 24\cdot 25\cdot (2\cdot 24+1) = 4900 = 70^2$ であるから, $(x,y) = (24,70)$ は $[*]$ を満たす.
参考
- 正の整数 $x,$ $y$ を用いて $N = \dfrac{1}{6}x(x+1)(2x+1) = y^2$ の形に表される正の整数 $N$ は, $x$ 段の正四角錐状にも $y$ 行 $y$ 列の正方形状にも並べられるような球の個数であるから,「平方四角錐数」(square pyramidal number) と呼ばれる. $y^2 = \dfrac{1}{6}x(x+1)(2x+1)$ が $(x,y) = (1,1),$ $(24,70)$ 以外の正の整数解をもつか, つまり「平方四角錐数」が $1,$ $4900$ のみであるかという「リュカのキャノンボール問題」(Lucas' cannonball problem) は, $1918$ 年に肯定的に解決された.
- $f(x) = 0$ が重解をもたないような $3$ 次多項式 $f(x)$ を用いて $y^2 = f(x)$ で定義される曲線は, 「楕円曲線」(elliptic curve) と呼ばれ, 現代整数論の主要な研究対象である. この形の方程式は有理数係数の場合に高々有限個の整数解しかもたないという「ジーゲルの定理」(Siegel's theorem) が知られている.
クイズ《ハーディー=ラマヌジャンのタクシー数》
ラマヌジャンは療養中, ハーディー教授が見舞いに訪れた際に,
“乗ってきたタクシーの番号は $1729$ だった. さして特徴のない数字だったよ”という教授に対して, すぐさま
“そんなことはありません, とても興味深い数字です. それは $2$ つの立方数の和として $2$ 通りに表せる最小の数です”
と答えたという.
$1729$ は立方数の和としてどのように表されるか.
$2$ 通りの表し方を答えよ.
(有名問題, 参考: $2009$ 一橋大)
答え
$1729 = 1^3+12^3 = 9^3+10^3.$
解説
整数 $x,$ $y$ が $x^3+y^3 = 1729$ を満たすとし, $a = x+y,$ $b = x^2-xy+y^2$ とおく.
- (1)
- $a,$ $b$ を用いて $x$ を表す. $y = a-x$ を $x^2-xy+y^2 = b$ に代入して整理すると \[ 3x^2-3ax+a^2-b = 0\] となるから, $2$ 次方程式の解の公式により, $x$ は \[\begin{aligned} x &= \frac{3a\pm\sqrt{9a^2-12(a^2-b)}}{6} \\ &= \frac{3a\pm\sqrt{12b-3a^2}}{6} \quad \cdots [1] \end{aligned}\] と表される.
- (2)
- $a,$ $b > 0$ であることを示す.
$[1]$ は実数であるから,
$12b-3a^2 \geqq 0$ よって $b \geqq \dfrac{a^2}{4} \geqq 0$である. 一方, \[ ab = (x+y)(x^2-xy+y^2) = x^3+y^3 = 1729\] であるから, $a,$ $b > 0$ である.
- (3)
- $x^3+y^3 = 1729$ の整数解を求める. $[2]$ と \[ 1729 = 7\cdot 13\cdot 19\] から, \[ ab = 7\cdot 13\cdot 19\] が成り立つ. $a,$ $b$ は正の整数であるから, \[\begin{aligned} (a,b) = &(1,1729),\ (7,13\cdot 19),\ (13,7\cdot 19),\ (19,7\cdot 13),\\ &(7\cdot 13,19),\ (7\cdot 19,13),\ (13\cdot 19,7),\ (1729,1) \end{aligned}\] が成り立つ. このうち, $[1]$ が整数となるのは \[ (a,b) = (13,7\cdot 19),\ (19,7\cdot 13)\] の場合に限り, このとき \[ (x,y) = (1,12),\ (9,10),\ (10,9),\ (12,1)\] である. ゆえに, $1729$ は立方数の和として \[ 1729 = 1^3+12^3 = 9^3+10^3\] と $2$ 通りに表される.
参考
- $1729 = 1^3+12^3 = 9^3+10^3$ は $2$ 通りの立方数の和として表される最小の正の整数である. インドの魔術師という異名をもつ数学者 S・ラマヌジャンは療養中, G・H・ハーディーが見舞いに訪れた際に, “乗ってきたタクシーの番号は $1729$ だった. さして特徴のない数字だったよ”というハーディーに対して, すぐさま “そんなことはありません, とても興味深い数字です. それは $2$ つの立方数の和として $2$ 通りに表せる最小の数です” と答えたという. この逸話にちなんで, $1729$ は「ハーディー=ラマヌジャンのタクシー数」(Hardy–Ramanujan taxicab number) と呼ばれる.
- 本問の結果から, $1729$ は $3$ 通り以上の $2$ つの立方数の和としては表せないことがわかる.
クイズ《累乗の差》
バレーボール, キンボール ($3$ チームが $1$ つのコートに入って戦う球技) のトーナメント大会がそれぞれ開かれた.
$2$ つの大会の出場チーム数の差は $1$ であり, 各大会でどのチームも $1$ 回戦を戦ったという.
このとき, 各大会の出場チーム数はいくらか.
(オリジナル)
答え
$2$ チームと $3$ チーム, $4$ チームと $3$ チーム, または $8$ チームと $9$ チーム.
解説
バレーボール, キンボールの大会の決勝戦がそれぞれ $m$ 回戦, $n$ 回戦であるとき, 各大会の出場チーム数は $2^m,$ $3^n$ である.
よって, 方程式
\[ 2^m-3^n = \pm 1\]
を解けばよい.
- (1)
- 正の整数 $m,$ $n$ が
を満たすとする. このとき, \[ (-1)^m-1 \equiv 0 \pmod 3\] が成り立つから, $m$ は偶数である. そこで, $m = 2k$ ($k$: 正の整数) とおくと, \[ 3^n = 2^{2k}-1 = (2^k+1)(2^k-1)\] から,$2^m-3^n = 1$ つまり $2^m-1 = 3^n$
が得られる. このとき, $m = 2$ であるから, $3^n = 4-1 = 3$ よって $n = 1$ である.$(2^k-1,2^k+1) = (1,3)$ よって $k = 1$ - (2)
- 正の整数 $m,$ $n$ が
\[ 3^n-2^m = 1 \quad \cdots [\ast ]\]
を満たすとする.
まず, $m > 1$ ならば, $n$ は偶数であることを示す.
$m$ は整数であるから, $m > 1$ のとき, $m \geqq 2$ である.
このとき, 仮に $n$ が奇数であるとすると, $n = 2k+1$ ($k$: 非負整数) と書けて,
\[\begin{aligned}
3^n-2^m &= 3^{2k+1}-2^m = 3\cdot 9^k-4\cdot 2^{m-2} \\
&\equiv 3\cdot 1^k = 3 \pmod 4
\end{aligned}\]
となってしまうから, $n$ は偶数である.
これをもとにして, $[\ast ]$ の解を求める.- (i)
- $m = 1$ のとき. $(m,n) = (1,1)$ は $[\ast ]$ を満たす.
- (ii)
- $m > 1$ のとき. $n$ は偶数であるので, $n = 2k$ ($k$: 正の整数) と書けて \[\begin{aligned} [\ast ] &\iff 3^{2k}-1 = 2^m \\ &\iff (3^k+1)(3^k-1) = 2^m \end{aligned}\] となる. よって, ある非負整数 $i,$ $j$ に対して \[ 3^k+1 = 2^i, \quad 3^k-1 = 2^j, \quad i+j = m\] となり, 第 $1$ 式から第 $2$ 式を引くと \[ 2^i-2^j = (3^k+1)-(3^k-1)\] から \[ 2^j(2^{i-j}-1) = 2\] となるので, $j = i-j = 1$ から $(i,j) = (2,1)$ となる. このとき, $(m,n) = (3,2)$ である.
参考
「カタラン方程式」と呼ばれる方程式 $x^m-y^n = 1$ の $x,$ $y > 0,$ $m,$ $n > 1$ なる整数解は $(x,m,y,n) = (3,2,2,3)$ に限る,
つまり差が $1$ であるような正の累乗数は $9$ と $8$ のみであるというのが有名な「カタラン予想」(Catalan's conjecture) で,
2002 年に P・ミハイレスクによって肯定的に解決された.
クイズ《累乗の和》
三角柱, 四角柱, 五角柱の鉛筆があり, それらの側面には互いに異なる文字が $1$ 個ずつ彫られている.
A さんは三角柱, 四角柱の鉛筆のどちらかをランダムに選び, 三角柱の鉛筆であればそれを $x$ 回, 四角柱の鉛筆であればそれを $y$ 回転がす.
B さんは五角柱の鉛筆を $z$ 回転がす.
A さん, B さんの文字の出方の総数が一致するとき, $x,$ $y,$ $z$ の値はいくらか.
(オリジナル)
答え
$x = y = z = 2.$
解説
A さんの文字の出方は $3^x+4^y$ 通り, B さんの文字の出方は $5^z$ 通りあるから,
\[ 3^x+4^y = 5^z \quad \cdots [\ast ]\]
が成り立つ.
$(x,y,z) = (2,2,2)$ はこの方程式の解である.
以下, 正の整数 $x,$ $y,$ $z$ が $[\ast ]$ を満たすとして, $x = y = z$ であることを示す.
- (1)
- $x$ は偶数であることを示す. $3^x = 5^z-4^y$ かつ $3 \equiv -1,$ $5 \equiv 1 \pmod 4$ であるから, \[ (-1)^x \equiv 1^z-0^y = 1 \pmod 4\] が成り立つ. よって, $x$ は偶数である.
- (2)
- $z$ は偶数であることを示す. $5^z = 3^x+4^y$ かつ $5 \equiv -1,$ $4 \equiv 1 \pmod 3$ であるから, \[ (-1)^z \equiv 0^x+1^y = 1 \pmod 3\] が成り立つ. よって, $z$ は偶数である.
- (3)
- $5^{\frac{z}{2}}+3^{\frac{x}{2}} = 2^s,$ $5^{\frac{z}{2}}-3^{\frac{x}{2}} = 2^t,$ $s+t = 2y,$ $s > t$ を満たす正の整数 $s,$ $t$ が存在することを示し, $t$ の値を求める. $5^x-3^x = 4^y,$ (1), (2) により, \[ (5^{\frac{z}{2}}+3^{\frac{x}{2}})(5^{\frac{z}{2}}-3^{\frac{x}{2}}) = 2^{2y}\] が成り立つ. よって, \[ 5^{\frac{z}{2}}+3^{\frac{x}{2}} = 2^s, \quad 5^{\frac{z}{2}}-3^{\frac{x}{2}} = 2^t, \quad s+t = 2y, \quad s > t\] を満たす正の整数 $s,$ $t$ が存在する. 第 $1$ 式から第 $2$ 式を引いて $2$ で割ると, \[ 3^{\frac{x}{2}} = \frac{2^s-2^t}{2} = 2^{t-1}(2^{s-t}-1)\] が得られる. ここで, $3^{\frac{x}{2}},$ $2^{t-1},$ $2^{s-t}-1$ は正の整数であるから, $t = 1$ である.
- (4)
- $x = y = z = 2$ であることを示す. (3) により $s = 2y-1,$ $t = 1,$ したがって $2^{2y-2}-1 = 3^{\frac{x}{2}}$ であるから, \[ (2^{y-1}+1)(2^{y-1}-1) = 3^{\frac{x}{2}}\] が成り立つ. よって, \[ 2^{y-1}+1 = 3^u, \quad 2^{y-1}-1 = 3^v, \quad u+v = \frac{x}{2}, \quad u > v\] を満たす非負整数 $u,$ $v$ が存在する. 第 $1$ 式から第 $2$ 式を引くと, \[ 2 = 3^u-3^v = 3^v(3^{u-v}-1)\] が得られる. ここで, $3^v,$ $3^{u-v}-1$ は正の整数であるから, $(3^v,3^{u-v}-1) = (1,2)$ つまり $(u,v) = (1,0)$ である. このとき, $2^{y-1}-1 = 3^0 = 1$ から $y = 2$ であるので, $3^{\frac{x}{2}} = 2^{2\cdot 2-2}-1 = 3$ から $x = 2$ であり, さらに $5^z = 3^2+4^2 = 25$ から $z = 2$ が得られる. ゆえに, $x = y = z = 2$ である.
参考
本問は,「ピタゴラスの $3$ つ組」$(a,b,c)$ に対して
\[ a^x+b^y = c^z\]
の正の整数解は $(x,y,z) = (2,2,2)$ に限るという「イェスマノヴィッチ予想」 (Jesmanowicz conjecture) の $(a,b,c) = (3,4,5)$ の場合であり, 一般の場合は未解決である ($2024$ 年 $7$ 月現在).
次の場合などにこの予想が正しいことが確認されている.
- $(a,b,c) = (3,4,5)$ の場合 (Sierpinski, $1956$ 年).
- $(a,b,c) = (5,12,13),$ $(7,24,25),$ $(9,40,41),$ $(11,60,61)$ の場合 (Jesmanowicz, $1956$ 年).
- $(a,b,c) = (2k+1,2k(k+1),2k(k+1)+1)$ ($k$: 正の整数) の場合 (Demjanenko, $1965$ 年).
- $(a,b,c) = (4k^2-1,4k,4k^2+1)$ ($k$: 正の整数) の場合 (Grytczuk, Grelak, $1984$ 年).
- $(a,b,c) = (4k^2-p^2,4kp,4k^2+p^2)$ ($k$: 正の奇数, $p$: 素数, $p \equiv 3 \pmod 4$) かつ $y \neq 1$ の場合 (Takakuwa, Asaeda, $1993$ 年).
- $(a,b,c) = (4k^2-p^2,4kp,4k^2+p^2)$ ($k$: 正の奇数, $p$: 素数, $p \equiv 5 \pmod 8$) かつ $y$ が偶数の場合 (Takakuwa, $1993$ 年).
- $a,$ $b,$ $c$ が互いに素, $ab$ の素因数分解における $2$ の指数が $2,$ $c$ が奇素数の累乗の場合 (Le, $1995$ 年).
- $(a,b,c) = (m^2-n^2,2mn,m^2+n^2)$ ($m,$ $n$: 互いに素で偶奇の異なる正の整数, $m > n,$ $m$ の素因数分解における $2$ の指数が $1,$ $n \equiv 3 \pmod 4,$ $m \geqq 81n$) の場合 (Le, $1996$ 年).
クイズ《条件付きフェルマー方程式》
$n$ を正の整数とする.
$z \leqq n$ のとき, $x^n+y^n = z^n$ は正の整数解をもつか.
(参考: H・ステインハウス,『数学 100 の問題』, 問題 5)
答え
もたない.
解説
$x^n+y^n = z^n,$ $z \leqq n$ を満たす正の整数 $x,$ $y,$ $z$ が存在すると仮定する.
このとき, $x^n < z^n,$ $y^n < z^n$ から $x < z,$ $y < z$ が成り立つ.
$x \leqq y$ としても一般性を失わないから, その場合を考えると,
\[\begin{aligned}
z^n-y^n &= (z-y)(z^{n-1}+yz^{n-2}+\cdots +y^{n-2}z+y^{n-1}) \\
&> 1\cdot nx^{n-1} \quad (\because x \leqq y < z) \\
&> x^n \quad (\because x < z \leqq n)
\end{aligned}\]
となり, $x^n+y^n = z^n$ に反する.
ゆえに, $z \leqq n$ のとき, $x^n+y^n = z^n$ は正の整数解をもたない.
ゆえに, $z \leqq n$ のとき, $x^n+y^n = z^n$ は正の整数解をもたない.
クイズ《$3$ 種類のケーキ》
同じ大きさの $3$ 種類のホール型のケーキを, $1$ 切れの大きさが種類によって異なるように, それぞれ何等分かに切り分ける.
種類ごとに $1$ 切れずつ集めたときの合計の大きさが, $1$ ホール分未満で, できるだけ大きくなるようにするには, 各ケーキを何等分に切り分ければよいか.
(有名問題, 脚色あり, 参考: $2006$ 富山大)
答え
$1$ 切れの大きさが大きい方から順に $2$ 等分, $3$ 等分, $7$ 等分.
解説
$1$ 切れの大きさが大きい方から順に $x$ 等分, $y$ 等分, $z$ 等分であるとすると, 連立不等式
\[\frac{1}{x}+\frac{1}{y}+\frac{1}{z} < 1\ \cdots [1], \quad 0 < x < y < z\ \cdots [2]\]
が成り立つ.
よって, この整数解について, $[1]$ の左辺の最大値を求めればよい.
\[ S = \frac{1}{x}+\frac{1}{y}+\frac{1}{z}\]
とおく.
$y,$ $z > 0$ から $\dfrac{1}{y}+\dfrac{1}{z} > 0$ であるので, $x = 1$ は不適で, $x \geqq 2$ である.
これと $y > x$ から, $y \geqq 3$ であることが必要である.
- (i)
- $x = 2,$ $y = 3$ のとき. $[1]$ から \[ S = \frac{1}{2}+\frac{1}{3}+\frac{1}{z} < 1\] であるので, $\dfrac{1}{z} < \dfrac{1}{6},$ $z > 6$ つまり $z \geqq 7$ である. $S$ は $x,$ $y,$ $z$ に関してそれぞれ単調減少で, $\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{7} = \dfrac{41}{42} < 1$ であるから, $S$ は $(x,y,z) = (2,3,7)$ のとき最大値 $\dfrac{41}{42}$ をとる.
- (ii)
- $x = 2,$ $y \geqq 4$ のとき. $[2]$ から $z \geqq 5$ であり, $\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{5} = \dfrac{19}{20} < 1$ であるから, $S$ は $(x,y,z) = (2,4,5)$ のとき最大値 $\dfrac{19}{20}$ をとる.
- (iii)
- $x \geqq 3$ のとき. $[2]$ から $y \geqq 4,$ $z \geqq 5$ であり, $\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5} = \dfrac{47}{60} < 1$ であるから, $S$ は $(x,y,z) = (3,4,5)$ のとき最大値 $\dfrac{47}{60}$ をとる.
クイズ《$1$ 階と $2$ 階の部屋割り》
$1$ 階の $m$ 個の部屋には $n$ 人を泊め, $2$ 階の $n$ 個の部屋には $m$ 人を泊めた.
各階で考えられる部屋割りの総数は互いに等しく, 各階の宿泊者数は互いに異なるという.
このとき, 何人の宿泊者がいたか.
(有名問題)
答え
$6$ 人.
解説
- (1)
- $1$ 階, $2$ 階の考えられる部屋割りの総数はそれぞれ $m^n$ 通り, $n^m$ 通り. よって, $m^n = n^m,$ $m \neq n$ の正の整数解に対して $m+n$ の値を求めればよい. $m^n = n^m$ の両辺の $mn$ 乗根をとると, \[ m^{\frac{1}{m}} = n^{\frac{1}{n}} \quad \cdots [1]\] となる. \[ 0 < m < n \quad \cdots [2]\] としても一般性を失わない.
- (2)
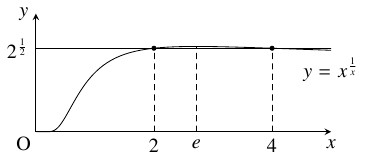
- $y = x^{\frac{1}{x}}$ の最大値を求める. $y > 0$ に注意して両辺の対数をとると, \[\log y = \frac{1}{x}\log x\] となる. 両辺を $x$ で微分すると \[\frac{y'}{y} = -\frac{1}{x^2}\cdot\log x+\frac{1}{x}\cdot\frac{1}{x} = \frac{1-\log x}{x^2}\] となるから, \[ y' = y\cdot\frac{1-\log x}{x^2} = x^{\frac{1}{x}-2}(1-\log x)\] である. $x^{\frac{1}{x}-2} > 0$ から \[\begin{aligned} y' \geqq 0 &\iff 1-\log x \geqq 0 \iff 0 < x \leqq e, \\ y' \leqq 0 &\iff x \geqq e \end{aligned}\] であるので, $y$ は $x = e$ で極大かつ最大の値 $e^{\frac{1}{e}}$ をとる.
- (3)
- 整数 $m,$ $n$ が $[1],$ $[2]$ を満たすとする.
(2) で見た $y = x^{\frac{1}{x}}$ の増減と $2 < e < 3$ から, $m = 1,$ $2$ が必要である.
$1^n = n^1$ の解は $n = 1$ に限るから, $m = 1$ は不適である.
したがって,
\[ x^{\frac{1}{x}} = 2^{\frac{1}{2}}\]
の正の整数解 $x\,(\neq 2)$ を求めればよい.
曲線 $y = x^{\frac{1}{x}}$ と直線 $y = 2^{\frac{1}{2}}$ はちょうど $2$ 点で交わるから,
$x^{\frac{1}{x}} = 2^{\frac{1}{2}}$ つまり $2^x = x^2$ は $x = 2$ 以外にただ $1$ つの実数解をもつ.
一方, $2^4 = 4^2 = 16$ であるから, それは $x = 4$ である. ゆえに, $[1],$ $[2]$ の整数解は $(m,n) = (2,4)$ であり, 求める宿泊者数は
である.$m+n = 2+4 = 6$ (人)