本格数学クイズ (数列)
数列
クイズ《$3$ 辺の長さが等差数列をなす直角三角形》
$3$ 辺の長さが等差数列をなすような直角三角形の $3$ 辺の長さの比はいくらか.
(有名問題)
答え
$3:4:5.$
解説
条件を満たす直角三角形の辺の長さを $a-d,$ $a,$ $a+d$ $(a > d > 0)$ とおく.
このとき, 三平方の定理により
\[\begin{aligned}
(a-d)^2+a^2 &= (a+d)^2 \\
a^2-2ad+d^2+a^2 &= a^2+2ad+d^2 \\
a^2 &= 4ad
\end{aligned}\]
が成り立つから, 両辺を $a\,(> 0)$ で割ると
\[ a = 4d\]
となる.
ゆえに, 条件を満たす直角三角形の $3$ 辺の長さの比は
\[ (a-d):a:(a+d) = 3d:4d:5d = 3:4:5\]
である.
クイズ《フォンタナの三角形》
番号札を A, B に配る.
番号の小さい方から A に $2$ 枚, B に $1$ 枚, $\cdots,$ A に $n+1$ 枚, B に $n$ 枚, $\cdots$ と配っていくとき, $n$ 回目に A に配られる札の番号の和 $S_n$ と B に配られる札の番号の和 $T_n$ の間にはどのような関係があるか.
| $S_n$ | $T_n$ |
| $1+2$ | $3$ |
| $4+5+6$ | $7+8$ |
| $9+10+11+12$ | $13+14+15$ |
| $16+17+18+19+20$ | $21+22+23+24$ |
| $25+26+27+28+29+30$ | $31+32+33+34+35$ |
| $\vdots$ | $\vdots$ |
(有名問題)
答え
$S_n = T_n.$
解説
$n-1$ 回目 $(n > 1)$ までに配られる札の枚数は
\[\begin{aligned}
(2+1)+\cdots +\{ n+(n-1)\} &= \sum_{k = 2}^n(2k-1) = \sum_{k = 1}^n(2k-1)-1 \\
&= 2\cdot\frac{n(n+1)}{2}-n-1 = n^2-1
\end{aligned}\]
であるから, $n$ 回目に A に配られる札の番号は $n^2$ から $n^2+n,$ B に配られる札の番号は $n^2+n+1$ から $n^2+2n$ である.
これは $n = 1$ のときも成り立つ. $\cdots [1]$
よって, 等差数列の和の公式により \[\begin{aligned} S_n &= n^2+\cdots +(n^2+n) = \frac{n+1}{2}\{ n^2+(n^2+n)\} \\ &= \frac{n+1}{2}(2n^2+n) = \frac{n(n+1)(2n+1)}{2}, \\ T_n &= (n^2+n+1)+\cdots +(n^2+2n) \\ &= \frac{n}{2}\{ (n^2+n+1)+(n^2+2n)\} \\ &= \frac{n}{2}(2n^2+3n+1) = \frac{n(n+1)(2n+1)}{2} \end{aligned}\] であるから, \[ S_n = T_n\] が成り立つ.
よって, 等差数列の和の公式により \[\begin{aligned} S_n &= n^2+\cdots +(n^2+n) = \frac{n+1}{2}\{ n^2+(n^2+n)\} \\ &= \frac{n+1}{2}(2n^2+n) = \frac{n(n+1)(2n+1)}{2}, \\ T_n &= (n^2+n+1)+\cdots +(n^2+2n) \\ &= \frac{n}{2}\{ (n^2+n+1)+(n^2+2n)\} \\ &= \frac{n}{2}(2n^2+3n+1) = \frac{n(n+1)(2n+1)}{2} \end{aligned}\] であるから, \[ S_n = T_n\] が成り立つ.
別解: $[1]$ 以降
$S_n$ の第 $1$ 項 $n^2$ を $n$ 個の $n$ の和に分けて残りの項に含めると,
\[\begin{aligned}
S_n &= n^2+(n^2+1)+\cdots +(n^2+n) \\
&= \overbrace{n+\cdots +n}^n+(n^2+1)+\cdots +(n^2+n) \\
&= \{ (n^2+1)+n\} +\cdots +\{ (n^2+n)+n\} \\
&= (n^2+n+1)+\cdots +(n^2+2n) \\
&= T_n
\end{aligned}\]
が得られる.
参考
- 本問の等式を $n$ が小さい順に並べてできる三角形 \[\begin{aligned} 1+2 &= 3, \\ 4+5+6 &= 7+8, \\ 9+10+11+12 &= 13+14+15, \\ 16+17+18+19+20 &= 21+22+23+24, \\ 25+26+27+28+29+30 &= 31+32+33+34+35, \\ &\ \ \vdots \end{aligned}\] を「フォンタナの三角形」(俗称「タルタリアの三角形」) と呼ぶ.
- 平方数の和については, すべての正の整数 $n$ に対して \[\begin{aligned} \sum_{k = 0}^n(2n^2+n+k)^2 &= \sum_{k = n+1}^{2n}(2n^2+n+k)^2 \\ &= \frac{n(n+1)(2n+1)(12n^2+12n+1)}{6} \end{aligned}\] が成り立つ.
クイズ《カードの番号の積の総和の最大値》
A, B がそれぞれ $1$ 番から $n$ 番までの番号札を持っている.
A, B が手札から $1$ 枚ずつ同時に番号札を切っていくとき, 各回の番号の積の総和は最大でいくらになるか.
(有名問題)
答え
$\dfrac{1}{6}n(n+1)(2n+1).$
解説
A, B が $k$ 回目に切る札の番号をそれぞれ $a_k,$ $b_k$ とおく.
このとき,
\[\{ a_1,\cdots,a_n\} = \{ b_1,\cdots,b_n\} = \{ 1,\cdots,n\}\]
であり, 数列 $\{ a_kb_k\}$ の和の最大値を求めればよい.
$b_k$ の値が小さい順に加えても和の値は変わらないから,
\[ S = \sum_{k = 1}^nka_k\]
の最大値を求めればよい.
$(a_k-k)^2 = a_k{}^2-2ka_k+k^2$ であるから,
\[ ka_k = \frac{1}{2}\{ a_k{}^2+k^2-(a_k-k)^2\}\]
が成り立つ.
$k = 1,$ $\cdots,$ $n$ を代入して辺々を加えると
\[\begin{aligned}
S &= \sum_{k = 1}^nka_k \\
&= \frac{1}{2}\left\{\sum_{k = 1}^na_k{}^2+\sum_{k = 1}^nk^2-\sum_{k = 1}^n(a_k-k)^2\right\} \\
&= \sum_{k = 1}^nk^2-\frac{1}{2}\sum_{k = 1}^n(a_k-k)^2 \\
&= \frac{1}{6}n(n+1)(2n+1)-\frac{1}{2}\sum_{k = 1}^n(a_k-k)^2
\end{aligned}\]
が得られるから, $S$ は $a_k = k$ $(1 \leqq k \leqq n)$ のとき最大値
\[\frac{1}{6}n(n+1)(2n+1)\]
をとる.
クイズ《ハノイの塔》
地面に $3$ 本の棒 A, B, C が立てられており, 棒 A に穴の開いた半径の異なる $n$ 枚の円盤が半径の大きい順に通されている.
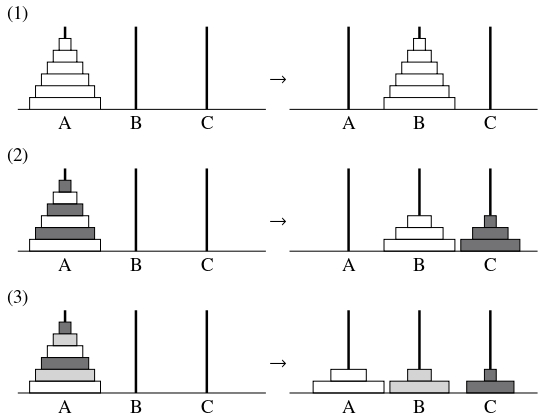
- (1)
- すべての円盤を棒 B に移す手数の最小値はいくらか.
- (2)
- 円盤に半径の大きい方から $2$ 枚ごとに白色, 黒色の順に色が塗られているとする. 白色の円盤を棒 B, 黒色の円盤を棒 C に移す手数の最小値はいくらか.
- (2)'
- (2) の最後の状態から棒 B と棒 C の円盤を入れ替える手数の最小値はいくらか.
- (3)
- 円盤に半径の大きい方から $3$ 枚ごとに白色, 灰色, 黒色の順に色が塗られているとする. 白色の円盤を棒 A, 灰色の円盤を棒 B, 黒色の円盤を棒 C に移す手数の最小値はいくらか.
(有名問題)

答え
- (1)
- $2^n-1.$
- (2)
- $n$ が $3$ の倍数のとき $\dfrac{5\cdot 2^n-5}{7},$ $n$ を $3$ で割った余りが $1$ のとき $\dfrac{5\cdot 2^n-3}{7},$ $n$ を $3$ で割った余りが $2$ のとき $\dfrac{5\cdot 2^n-6}{7}.$
- (2)'
- $n$ が $3$ の倍数のとき $\dfrac{5\cdot 2^n-5}{7},$ $n$ を $3$ で割った余りが $1$ のとき $\dfrac{5\cdot 2^n-3}{7},$ $n$ を $3$ で割った余りが $2$ のとき $\dfrac{5\cdot 2^n+1}{7}.$
- (3)
- $n$ が偶数のとき $\dfrac{2^n-1}{3},$ $n$ が奇数のとき $\dfrac{2^n-2}{3}.$
解説
- (1)
- $1$ 本の棒の最も上にある $n$ 枚を別の棒の最も上に移すときの手数の最小値を $a_n$ とおく.
棒 A の最も上にある $n+1$ 枚を棒 B の最も上に移すためには, まず上の $n$ 枚を棒 C に移し, 次に棒 A に残された $1$ 枚を棒 B に移し, 最後に棒 C に移された $n$ 枚を棒 B に移す必要がある.
よって,
\[ a_{n+1} = a_n+1+a_n = 2a_n+1 \quad \cdots [1]\]
が成り立つ.
\[ \alpha = 2\alpha +1 \quad \cdots [2]\] を解くと $\alpha = -1$ となるので, $[1]-[2]$ から
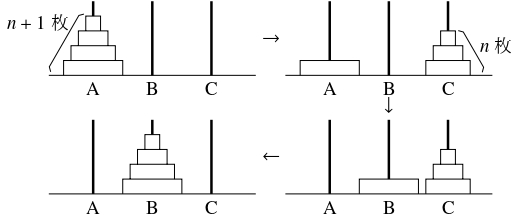
となる. $\{ a_n+1\}$ は初項 $a_1+1 = 1+1 = 2,$ 公比 $2$ の等比数列であるから,$a_{n+1}-\alpha = 2(a_n-\alpha )$ つまり $a_{n+1}+1 = 2(a_n+1)$
である.$a_n+1 = 2^n$ つまり $a_n = 2^n-1$ - (2)
- 棒 A の最も上にある $n$ 枚のうち, 白色の円盤を棒 B, 黒色の円盤を棒 C に移す (以下, 色ごとに分けるという) 手数の最小値を $b_n$ とおく.
棒 A の $n+3$ 枚を色ごとに分けるためには, まず上の $n+2$ 枚を棒 C に移してから残りの $1$ 枚を棒 B に移し,
次に棒 C に移された $n+2$ 枚のうち $n$ 枚を棒 A に移してから残りの $2$ 枚のうち上の $1$ 枚のみを棒 B に移し (下の $1$ 枚は動かす必要はない),
最後に棒 A に戻された $n$ 枚を色ごとに分ける必要がある.
よって,
\[ b_{n+3} = a_{n+2}+1+a_n+1+b_n\]
が成り立つから, (1) とあわせると
\[ b_{n+3}-b_n = 2^{n+2}+2^n = 5\cdot 2^n\]
が得られる.
また, 明らかに
\[ b_1 = 1, \quad b_2 = 2, \quad b_3 = 5\]
である.
- (i)
- $n = 3q$ ($q$: 正の整数) のとき. $q \geqq 2$ のとき \[\begin{aligned} b_n &= b_3+\sum_{k = 1}^{q-1}(b_{3k+3}-b_{3k}) \\ &= 5+\sum_{k = 1}^{q-1}5\cdot 2^{3k} = \sum_{k = 0}^{q-1}5\cdot 8^k \\ &= 5\cdot\frac{8^q-1}{8-1} = \frac{5\cdot 2^{3q}-5}{7} = \frac{5\cdot 2^n-5}{7} \end{aligned}\] であり, これは $q = 1$ のときも成り立つ.
- (ii)
- $n = 3q-2$ ($q$: 正の整数) のとき. $q \geqq 2$ のとき \[\begin{aligned} b_n &= b_1+\sum_{k = 1}^{q-1}(b_{3k+1}-b_{3k-2}) \\ &= 1+\sum_{k = 1}^{q-1}5\cdot 2^{3k-2} = 1+\sum_{k = 1}^{q-1}10\cdot 8^{k-1} \\ &= 1+10\cdot\frac{8^{q-1}-1}{8-1} = \frac{5\cdot 2^{3q-2}-3}{7} = \frac{5\cdot 2^n-3}{7} \end{aligned}\] であり, これは $q = 1$ のときも成り立つ.
- (iii)
- $n = 3q-1$ ($q$: 正の整数) のとき. $q \geqq 2$ のとき \[\begin{aligned} b_n &= b_2+\sum_{k = 1}^{q-1}(b_{3k+2}-b_{3k-1}) \\ &= 2+\sum_{k = 1}^{q-1}5\cdot 2^{3k-1} = 2+\sum_{k = 1}^{q-1}20\cdot 8^{k-1} \\ &= 2+20\cdot\frac{8^{q-1}-1}{8-1} = \frac{5\cdot 2^{3q-1}-6}{7} = \frac{5\cdot 2^n-6}{7} \end{aligned}\] であり, これは $q = 1$ のときも成り立つ.
- (2)'
- 求める手数の最小値を $b'_n$ とおく.
明らかに, $b'_1 = 1$ である.
$n > 1$ のとき, (2) の最後の状態から棒 B と棒 C の円盤を入れ替えるためには, まず最も大きい円盤以外を棒 A に戻し ((2) で $n-1$ 枚を色ごとに分ける操作の逆), 棒 B, C の間で最も大きい円盤の位置を入れ替え, 最後に棒 A に移された $n-1$ 枚を色ごとに分ける必要がある.
よって,
\[ b'_n = b_{n-1}+1+b_{n-1} = 2b_{n-1}+1\]
が成り立つ.
- (i)
- $n = 3q$ ($q$: 正の整数) のとき. (2) の (iii) の結果により, \[ b'_n = 2\cdot\frac{5\cdot 2^{n-1}-6}{7}+1 = \frac{5\cdot 2^n-5}{7}\] が成り立つ.
- (ii)
- $n = 3q-2$ ($q$: 正の整数) のとき. $q \geqq 2$ のとき, (2) の (i) の結果により, \[ b'_n = 2\cdot\frac{5\cdot 2^{n-1}-5}{7}+1 = \frac{5\cdot 2^n-3}{7}\] が成り立つ. これは $n = 1$ のときも成り立つ.
- (iii)
- $n = 3q-1$ ($q$: 正の整数) のとき. (2) の (ii) の結果により, \[ b'_n = 2\cdot\frac{5\cdot 2^{n-1}-3}{7}+1 = \frac{5\cdot 2^n+1}{7}\] が成り立つ.
- (3)
- $1$ 本の棒の最も上にある $n$ 枚のうち, 一番下の $1$ 枚を動かさずに, 白色の円盤を棒 A, 灰色の円盤を棒 B, 黒色の円盤を棒 C に移す (以下, 色ごとに移すという) 手数の最小値を $c_n$ とおく.
棒 A の $n+2$ 枚を色ごとに移すためには, まず上の $n$ 枚を棒 C に移してから残りの $1$ 枚を棒 B に移し, 最後に棒 C に移された $n$ 枚を色ごとに移す必要がある.
よって,
\[ c_{n+2} = a_n+1+c_n\]
が成り立つから, (1) とあわせると
\[ c_{n+2}-c_n = 2^n\]
が得られる.
また, 明らかに
\[ c_1 = 0, \quad c_2 = 1\]
である.
- (i)
- $n = 2q$ ($q$: 正の整数) のとき. $q \geqq 2$ のとき \[\begin{aligned} c_n &= c_2+\sum_{k = 1}^{q-1}(c_{2k+2}-c_{2k}) \\ &= 1+\sum_{k = 1}^{q-1}2^{2k} = \sum_{k = 0}^{q-1}4^k \\ &= \frac{4^q-1}{4-1} = \frac{2^{2q}-1}{3} = \frac{2^n-1}{3} \end{aligned}\] であり, これは $q = 1$ のときも成り立つ.
- (ii)
- $n = 2q-1$ ($q$: 正の整数) のとき. $q \geqq 2$ のとき \[\begin{aligned} c_n &= c_1+\sum_{k = 1}^{q-1}(c_{2k+1}-c_{2k-1}) \\ &= \sum_{k = 1}^{q-1}2^{2k-1} = \sum_{k = 1}^{q-1}2\cdot 4^{k-1} \\ &= 2\cdot\frac{4^{q-1}-1}{4-1} = \frac{2^{2q-1}-2}{3} = \frac{2^n-2}{3} \end{aligned}\] であり, これは $q = 1$ のときも成り立つ.
クイズ《うなぎの寝床での畳の敷き方》
ちょうど $n$ 枚の畳が敷けるような長方形のうなぎの寝床に畳を敷く方法は何通りあるか.
ただし, 寝床の縦の長さは畳の長い方の辺の長さに等しく, 横の長さは畳の短い方の辺の長さの $n$ 倍に等しいとする.
(有名問題)
答え
$\displaystyle\frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^{n+1}-\left(\frac{1-\sqrt 5}{2}\right) ^{n+1}\right\}$ 通り.
解説
畳をすべて縦に敷いたとき縦に $1$ 枚, 横に $n$ 枚の畳が敷けるようなうなぎの寝床において, 畳の敷き方の総数を $a_n$ とおく.
- (1)
- まず, 数列 $\{ a_n\}$ が満たす漸化式を求める.
$n > 2$ のとき, 最後に敷く畳の向きに着目すると, 次の $2$ つの場合が考えられる.
- (i)
- 最後に畳を横に敷く場合. $n$ 枚の畳を敷く方法は, $n-2$ 枚の畳の敷き方 $a_{n-2}$ 通りだけある.
- (ii)
- 最後に畳を縦に敷く場合. $n$ 枚の畳を敷く方法は, $n-1$ 枚の畳の敷き方 $a_{n-1}$ 通りだけある.
- (2)
- 次に, 数列 $\{ a_{n+1}-\alpha a_n\},$ $\{ a_{n+1}-\beta a_n\}$ がそれぞれ公比 $\beta,$ $\alpha$ の等比数列になるような定数 $\alpha,$ $\beta\ (\alpha > \beta )$ を求める. このとき, \[\begin{aligned} a_{n+2}-\alpha a_{n+1} &= \beta (a_{n+1}-\alpha a_n), \\ a_{n+2}-\beta a_{n+1} &= \alpha (a_{n+1}-\beta a_n) \end{aligned}\] から \[ a_{n+2} = (\alpha +\beta )a_{n+1}-\alpha\beta a_n \quad \cdots [2]\] が成り立つ. $[1],$ $[2]$ から, \[\alpha +\beta = 1,\quad \alpha\beta = -1\] が成り立てばよい. このとき, $\alpha,$ $\beta$ は $2$ 次方程式 $x^2-x-1 = 0$ の解であるから, 条件を満たす $\alpha,$ $\beta$ の組として \[ (\alpha,\beta ) = \left(\frac{1+\sqrt 5}{2},\frac{1-\sqrt 5}{2}\right)\] がとれる.
- (3)
- 最後に, 数列 $\{ a_n\}$ の一般項を求める. $a_1 = 1,$ $a_2 = 2$ である. よって, 数列 $\{ a_{n+1}-\alpha a_n\},$ $\{ a_{n+1}-\beta a_n\}$ の初項は, それぞれ \[\begin{aligned} a_2-\alpha a_1 = 2-\alpha &= \frac{3-\sqrt 5}{2} = \beta ^2, \\ a_2-\beta a_1 = 2-\beta &= \frac{3+\sqrt 5}{2} = \alpha ^2 \end{aligned}\] である. したがって, $\alpha,$ $\beta$ のとり方から, \[\begin{aligned} a_{n+1}-\alpha a_n &= \beta ^{n+1}, \\ a_{n+1}-\beta a_n &= \alpha ^{n+1} \end{aligned}\] が成り立つ. 辺々を引くと \[ (\alpha -\beta )a_n = \alpha ^{n+1}-\beta ^{n+1}\] となるので, $\alpha -\beta = \sqrt 5$ から \[ a_n = \frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^{n+1}-\left(\frac{1-\sqrt 5}{2}\right) ^{n+1}\right\}\] が成り立つ.
参考
- 数列 $\{ a_n\}$ は「フィボナッチ数列」$\{ F_n\}$ の第 $2$ 項以降を順に並べて得られる数列である. つまり, $a_n = F_{n+1}$ である.
- 初期条件 $F_1 = F_2 = 1$ と漸化式 $F_{n+2} = F_n+F_{n+1}$ で定まる数列 \[\{ F_n\}:1,1,2,3,5,8,13,21,34,55,89,144,\cdots\] を「フィボナッチ数列」(Fibonacci sequence) と呼ぶ. この数列の項は「フィボナッチ数」と呼ばれ, 花びらの枚数, 植物の種が並んでできるらせんの本数など, 自然界でよく見られる整数である.
- 公式 \[ F_n = \frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^n-\left(\frac{1-\sqrt 5}{2}\right) ^n\right\}\] は「ビネの公式」(Binet's formula) として知られている.
- $n$ 番目の「フィボナッチ数」$F_n$ は $\dfrac{1}{\sqrt 5}\left(\dfrac{1+\sqrt 5}{2}\right) ^n+\dfrac{1}{2}$ の整数部分に等しい. 実際,「ビネの公式」 \[ F_n = \frac{\alpha ^n-\beta ^n}{\sqrt 5}\] と $-1 < \beta < 0,$ $\sqrt 5 > 2$ により \[\left| F_n-\frac{\alpha ^n}{\sqrt 5}\right| = \left| -\frac{\beta ^n}{\sqrt 5}\right| = \frac{|\beta |^n}{\sqrt 5} < \frac{1}{2}\] であるから, \[\begin{aligned} -\frac{1}{2} &< F_n-\frac{\alpha ^n}{\sqrt 5} < \frac{1}{2} \\ \left(\frac{\alpha ^n}{\sqrt 5}+\frac{1}{2}\right) -1 = \frac{\alpha ^n}{\sqrt 5}-\frac{1}{2} &< F_n < \frac{\alpha ^n}{\sqrt 5}+\frac{1}{2} \end{aligned}\] が成り立つ. $F_n$ は整数であるから, これは $\dfrac{\alpha ^n}{\sqrt 5}+\dfrac{1}{2}$ の整数部分が $F_n$ に等しいことを意味する.
- 「フィボナッチ数列」の隣り合う項の比は「黄金比」$1:\dfrac{1+\sqrt 5}{2}$ に限りなく近づいていくこともよく知られている (こちらを参照).
クイズ《$1$ 段飛ばしを許した階段の登り方》
$1$ 歩目は $1$ 段だけ上るとし, $2$ 歩目以降は $1$ 歩で $1$ 段上ることも $2$ 段上ることもできるとするとき, $n$ 段以下の階段を上る方法は全部で何通りあるか.
(有名問題)
答え
$\displaystyle\frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^{n+2}-\left(\frac{1-\sqrt 5}{2}\right) ^{n+2}\right\}-1$ 通り.
解説
与えられたルールのもとで $n$ 段の階段を上る方法の総数を $F_n$ とおく.
また, $n$ 段以下の階段を上る方法の総数を $S_n$ とおく.
- (1)
- $n+2$ 段の階段を上るとき, 最後の $1$ 歩に着目すると, 次の $2$ つの場合が考えられる.
- (i)
- 最後の $1$ 歩で $2$ 段上る場合. $n+2$ 段を上る方法は, $n$ 段の上り方 $F_n$ 通りだけある.
- (ii)
- 最後の $1$ 歩で $1$ 段上る場合. $n+2$ 段を上る方法は, $n+1$ 段の上り方 $F_{n+1}$ 通りだけある.
- (2)
- $S_n = F_1+\cdots +F_n$ であるから, \[ F_k = -F_{k+1}+F_{k+2} \quad (1 \leqq k \leqq n)\] の辺々を加えると \[\begin{aligned} S_n &= (-F_2+F_3)+\cdots +(-F_{n+1}+F_{n+2}) \\ &= -F_2+F_{n+2} \\ &= F_{n+2}-1 \\ &= \frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^{n+2}-\left(\frac{1-\sqrt 5}{2}\right) ^{n+2}\right\} -1 \end{aligned}\] が得られる.
クイズ《円卓における席替え》
それぞれが動かないか隣に移るように円卓の周りに座った $n$ 人 $(n \geqq 3)$ を並べ替える方法は何通りあるか.
(有名問題)
答え
$\left(\dfrac{1+\sqrt 5}{2}\right) ^n+\left(\dfrac{1-\sqrt 5}{2}\right) ^n$ 通り.
解説
- (1)
- まず, それぞれが動かないか隣に移るように $1$ 列に並んだ $n$ 人を並べ替える方法の総数 $a_n$ を求める.
- (i)
- 最後尾の人が隣に移る場合. $n$ 人を並べ替える方法は, $n-2$ 人の並べ方 $a_{n-2}$ 通りだけある.
- (ii)
- 最後尾の人が動かない場合. $n$ 人を並べ替える方法は, $n-1$ 人の並べ方 $a_{n-1}$ 通りだけある.
- (2)
- $n$ 人の列の先頭と最後尾をつなげて, $n$ 人を円形に並べる.
求める場合の数を $L_n$ とおく.
- (i)
- 先頭と最後尾の人が入れ替わる場合. $n$ 人を並べ替える方法は, 列における $n-2$ 人の並べ方 $a_{n-2}$ 通りだけある.
- (ii)
- 先頭と最後尾の人が入れ替わらない場合. $n$ 人を並べ替える方法は, 列における $n$ 人の並べ方 $a_n$ 通りだけある.
参考
数列 $\{ L_n\}$ は「リュカ数列」(Lucas sequence) として知られている.
クイズ《正四面体の辺上のランダム・ウォーク》
正四面体 $\mathrm{ABCD}$ の頂点 $\mathrm A$ にいるアリが $1$ 秒ごとに異なる頂点に等確率で移動していくとき, $n$ 秒後に頂点 $\mathrm A$ にいる確率はいくらか.
(有名問題)
答え
$\dfrac{1}{4}+\dfrac{3}{4}\left( -\dfrac{1}{3}\right) ^n.$
解説
アリが $n$ 秒後に頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ にいる確率をそれぞれ $a_n,$ $b_n,$ $c_n,$ $d_n$ とおく.
このとき,
\[\begin{aligned}
&a_{n+1} = \frac{1}{3}b_n+\frac{1}{3}c_n+\frac{1}{3}d_n, \\
&a_n+b_n+c_n+d_n = 1
\end{aligned}\]
であるから,
$a_{n+1} = \dfrac{1}{3}(1-a_n)$ つまり $a_{n+1} = -\dfrac{1}{3}a_n+\dfrac{1}{3}$
が成り立つ.
両辺から $\alpha = -\dfrac{1}{3}\alpha +\dfrac{1}{3}$ の解 $\alpha = \dfrac{1}{4}$ を引いて整理すると,
\[ a_{n+1}-\frac{1}{4} = -\frac{1}{3}\left( a_n-\frac{1}{4}\right)\]
が得られる.
よって, $\left\{ a_n-\dfrac{1}{4}\right\}$ は第 $0$ 項 $a_0-\dfrac{1}{4} = 1-\dfrac{1}{4} = \dfrac{3}{4},$ 公比 $-\dfrac{1}{3}$ の等比数列であるから,
$a_n-\dfrac{1}{4} = \dfrac{3}{4}\left( -\dfrac{1}{3}\right) ^n$ つまり $a_n = \dfrac{1}{4}+\dfrac{3}{4}\left( -\dfrac{1}{3}\right) ^n$
である.
参考
アリが正三角形の辺上を動く場合については, こちらを参照.
クイズ《$1$ 人飛ばしの継子立て》
出席番号が $1$ 番から $n$ 番までの $n$ 人の生徒が順に $1$ つの輪を作るように並んでいる.
出席番号が $2$ 番の生徒から $1$ 人飛ばしで $1$ 人ずつ輪から抜けていくとき, 最後に残った生徒の出席番号はいくらか.
ただし, $1$ 人飛ばしというルールは, 各時点で残っている生徒に対して考えるものとする.
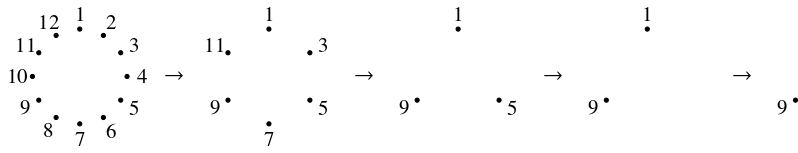
(有名問題)
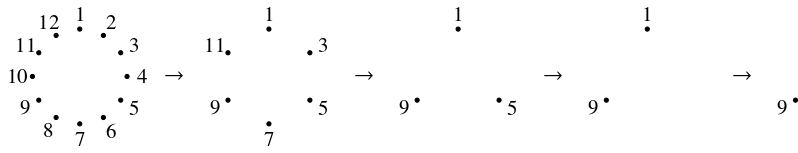
答え
$n = 2^m+r$ ($m$: 非負整数, $0 \leqq r < 2^m$) のとき, $2r+1$ 番の生徒.
解説
最後に残った生徒の出席番号を $f(n)$ とおく.
数値実験として, $1 \leqq n \leqq 30$ における $f(n)$ の値を求めると, 次のようになる.
表をよく観察すると, $n = 2^m+r$ ($m$: 非負整数, $0 \leqq r < 2^m$) のとき
\[ f(n) = 2r+1 \quad \cdots [*]\]
が成り立つと予想できるから, $n$ に関する数学帰納法でこれを示す.
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| $f(n)$ | $1$ | $1$ | $3$ | $1$ | $3$ | $5$ | $7$ | $1$ | $3$ | $5$ |
| $n$ | $11$ | $12$ | $13$ | $14$ | $15$ | $16$ | $17$ | $18$ | $19$ | $20$ |
| $f(n)$ | $7$ | $9$ | $11$ | $13$ | $15$ | $1$ | $3$ | $5$ | $7$ | $9$ |
| $n$ | $21$ | $22$ | $23$ | $24$ | $25$ | $26$ | $27$ | $28$ | $29$ | $30$ |
| $f(n)$ | $11$ | $13$ | $15$ | $17$ | $19$ | $21$ | $23$ | $25$ | $27$ | $29$ |
- (1)
- 証明に用いる数列 $\{ f(n)\}$ の漸化式を求める.
番号の偶奇に着目すると, $f(1) = 1$ から
\[\begin{aligned}
f(2) &= 1 = 2f(1)-1, & f(3) &= 3 = 2f(1)+1, \\
f(4) &= 1 = 2f(2)-1, & f(5) &= 3 = 2f(2)+1, \\
f(6) &= 5 = 2f(3)-1, & f(7) &= 7 = 2f(3)+1
\end{aligned}\]
となり,
\[ f(2n) = 2f(n)-1, \quad f(2n+1) = 2f(n)+1\]
が成り立つと予想できるから, これを示す.
- 生徒が $2n$ 人の場合. $n$ 人が輪から抜けたとき, 出席番号が \[ 1,\ \cdots,\ 2k-1,\ \cdots,\ 2n-1\] の $n$ 人の生徒が残っている. 最後の $1$ 人になるまで操作を続けると, このうちの $f(n)$ 番目の生徒が最後に残るから, その生徒の出席番号は \[ f(2n) = 2f(n)-1\] である.
- 生徒が $2n+1$ 人の場合. $n+1$ 人が輪から抜けたとき, 出席番号が \[ 3,\ \cdots,\ 2k+1,\ \cdots,\ 2n+1\] の $n$ 人の生徒が残っている. 最後の $1$ 人になるまで操作を続けると, このうちの $f(n)$ 番目の生徒が最後に残るから, その生徒の出席番号は \[ f(2n+1) = 2f(n)+1\] である.
- (2)
- 上記の予想を示す.
- (i)
- $f(1) = 1 = 2\cdot 0+1$ であるから, $n = 1$ のとき $[*]$ が成り立つ.
- (ii)
- $n > 1$ として, $n$ 未満のすべての正の整数に対して $[*]$ が成り立つとする.
- $n$ が偶数の場合. $r$ は偶数であり, \[\frac{n}{2} = 2^{m-1}+\frac{r}{2}\] であるから, \[\begin{aligned} f(n) &= f\left( 2\cdot\frac{n}{2}\right) \\ &= 2f\left(\frac{n}{2}\right) -1 \quad (\because (1)) \\ &= 2\left( 2\cdot\frac{r}{2}+1\right) -1 = 2r+1 \end{aligned}\] が成り立つ.
- $n$ が偶数の場合. $r$ は奇数であり, \[\frac{n-1}{2} = 2^{m-1}+\frac{r-1}{2}\] であるから, \[\begin{aligned} f(n) &= f\left( 2\cdot\frac{n-1}{2}+1\right) \\ &= 2f\left(\frac{n-1}{2}\right) +1 \quad (\because (1)) \\ &= 2\left( 2\cdot\frac{r-1}{2}+1\right) +1 = 2r+1 \end{aligned}\] が成り立つ.