本格数学クイズ (極限)
数列の極限
クイズ《方眼の中の正方形》
$n\times n$ マスの方眼の罫線に沿って描かれた正方形がマス目全体に占める面積の割合として見込まれる値は, $n$ が大きくなるにつれてどのような値に近づいていくか.
(オリジナル)
答え
$\dfrac{1}{10}.$
解説
$n\times n$ マスの方眼の罫線に沿って正方形を描けるだけ描くとき, 正方形がマス目全体に占める面積の割合の平均値を $a_n$ とおく.
求めるべきは, 極限値 $\displaystyle\lim\limits_{n \to \infty}a_n$ である.
方眼のマス目の $1$ 辺の長さが $1$ であるとする.
- (1)
- 数列 $\{ a_n\}$ の一般項を求める.
- 正方形の個数は, $1$ 辺の長さが $k$ $(1 \leqq k \leqq n)$ である正方形が $(n-k+1)^2$ 個あることから, \[\sum_{k = 1}^n(n-k+1)^2 = \sum_{k = 1}^nk^2 = \frac{1}{6}n(n+1)(2n+1) \quad \cdots [1]\] である.
- 正方形ののべ面積は, \[\begin{aligned} &\sum_{k = 1}^n(n-k+1)^2k^2 \\ &= \sum_{k = 1}^n\{ (n+1)^2-2(n+1)k+k^2\} k^2 \\ &= \sum_{k = 1}^n\{ (n+1)^2k^2-2(n+1)k^3+k^4\} \\ &= (n+1)^2\sum_{k = 1}^nk^2-2(n+1)\sum_{k = 1}^nk^3+\sum_{k = 1}^nk^4 \\ &= (n+1)^2\cdot\frac{1}{6}n(n+1)(2n+1) \\ &\qquad -2(n+1)\cdot\frac{1}{4}n^2(n+1)^2 \\ &\qquad +\frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1) \\ &= \frac{1}{30}n(n+1)\{ 5(n+1)^2(2n+1) \\ &\qquad -15n(n+1)^2+(2n+1)(3n^2+3n-1)\} \\ &= \frac{1}{30}n(n+1)(n^3+4n^2+6n+4) \\ &= \frac{1}{30}n(n+1)(n+2)(n^2+2n+2) \quad \cdots [2] \end{aligned}\] である. ここで, \[\sum_{k = 1}^nk^4 = \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1)\] であることを使った.
- 正方形がマス目全体に占める面積の割合の平均値 $a_n$ は, 正方形の面積の平均値のマス目全体の面積に対する割合 $[2]\div [1]\div n^2$ に等しいから, \[\begin{aligned} a_n &= \frac{\dfrac{1}{30}n(n+1)(n+2)(n^2+2n+2)}{\dfrac{1}{6}n(n+1)(2n+1)\cdot n^2} \\ &= \frac{(n+2)(n^2+2n+2)}{5n^2(2n+1)} \end{aligned}\] である.
- (2)
- 極限値 $\lim\limits_{n \to \infty}a_n$ を求める. \[\begin{aligned} a_n &= \frac{(n+2)(n^2+2n+2)}{5n^2(2n+1)} = \frac{\left( 1+\dfrac{2}{n}\right)\left( 1+\dfrac{2}{n}+\dfrac{2}{n^2}\right)}{5\left( 2+\dfrac{1}{n}\right)} \\ &\to \frac{1}{10} \quad (n \to \infty ) \end{aligned}\] であるから, $\lim\limits_{n \to \infty}a_n = \dfrac{1}{10}$ である.
参考
このクイズの結果は高次元に一般化され,「$d$ 次元超立方体」における「標準大の超立方体」の「$d$ 次元体積」は $\dfrac{1}{{}_{2d+1}\mathrm C_d}$ である (こちらを参照; 廣津, $2021$ 年).
本問の答えの $10$ は ${}_{2\cdot 2+1}\mathrm C_2$ からきている.
クイズ《方眼の中の長方形》
$n\times n$ マスの方眼の罫線に沿って描かれた長方形がマス目全体に占める面積の割合として見込まれる値は, $n$ が大きくなるにつれてどのような値に近づいていくか.
(オリジナル)
答え
$\dfrac{1}{9}.$
解説
$n\times n$ マスの方眼の罫線に沿って長方形を描けるだけ描くとき, 長方形がマス目全体に占める面積の割合の平均値を $a_n$ とおく.
求めるべきは, 極限値 $\displaystyle\lim\limits_{n \to \infty}a_n$ である.
方眼のマス目の $1$ 辺の長さが $1$ であるとする.
- (1)
- 数列 $\{ a_n\}$ の一般項を求める.
- 長方形の個数は, 隣り合う $2$ 辺の長さが $k,$ $l$ $(1 \leqq k \leqq n,$ $1 \leqq l \leqq n)$ である長方形が $(n-k+1)(n-l+1)$ 個あることから, \[\begin{aligned} &\sum_{k = 1}^n\sum_{l = 1}^n(n-k+1)(n-l+1) \\ &= \sum_{k = 1}^n\sum_{l = 1}^nkl = \left(\sum_{k = 1}^nk\right)\left(\sum_{l = 1}^nl\right) = \left(\sum_{k = 1}^nk\right) ^2 \\ &= \left\{\frac{1}{2}n(n+1)\right\} ^2 \quad \cdots [1] \end{aligned}\] である.
- 長方形ののべ面積は, \[\begin{aligned} &\sum_{k = 1}^n\sum_{l = 1}^n(n-k+1)(n-l+1)kl \\ &= \left\{\sum_{k = 1}^n(n-k+1)k\right\}\left\{\sum_{l = 1}^n(n-l+1)l\right\} \\ &= \left\{\sum_{k = 1}^n(n-k+1)k\right\} ^2 \\ &= \left\{ \frac{1}{6}n(n+1)(n+2)\right\} ^2 \quad \cdots [2] \end{aligned}\] である. ここで, \[\begin{aligned} &\sum_{k = 1}^n(n-k+1)k = \sum_{k = 1}^n\{ (n+1)k-k^2\} \\ &= (n+1)\sum_{k = 1}^nk-\sum_{k = 1}^nk^2 \\ &= (n+1)\frac{1}{2}n(n+1)-\frac{1}{6}n(n+1)(2n+1) \\ &= \frac{1}{6}n(n+1)\{ 3(n+1)-(2n+1)\} \\ &= \frac{1}{6}n(n+1)(n+2) \end{aligned}\] であることを使った.
- 長方形がマス目全体に占める面積の割合の平均値 $a_n$ は, 長方形の面積の平均値のマス目全体の面積に対する割合 $[2]\div [1]\div n^2$ に等しいから, \[\frac{\left\{\dfrac{1}{6}n(n+1)(n+2)\right\} ^2}{\left\{\dfrac{1}{2}n(n+1)\right\} ^2\cdot n^2} = \frac{(n+2)^2}{9n^2}\] である.
- (2)
- 極限値 $\lim\limits_{n \to \infty}a_n$ を求める. \[ a_n = \frac{(n+2)^2}{9n^2} = \frac{1}{9}\left( 1+\dfrac{2}{n}\right) ^2 \to \frac{1}{9} \quad (n \to \infty )\] であるから, $\lim\limits_{n \to \infty}a_n = \dfrac{1}{9}$ である.
参考
本問の結果は高次元に一般化され,「$d$ 次元超立方体」における「標準大の超直方体」の「$d$ 次元体積」は $\dfrac{1}{3^d}$ である (こちらを参照; 廣津, $2021$ 年).
本問の答えの $9$ は $3^2$ からきている.
クイズ《長方形の辺長の比の極限値》
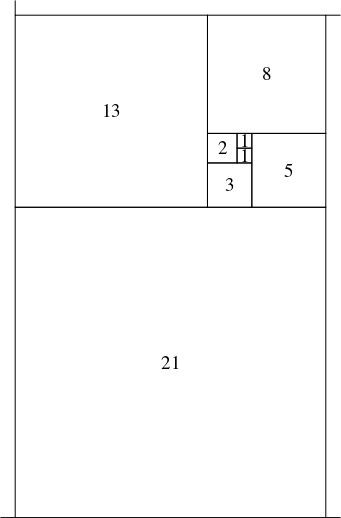
正方形の $1$ 辺に, それと $1$ 辺の長さが等しい正方形の辺を貼り合わせて長方形を作る.
その長い方の辺に, それと $1$ 辺の長さが等しい正方形の辺を貼り合わせて新たな長方形を作る.
この操作を続けるとき, 長方形の隣り合う $2$ 辺の長さの比はどのような値に近づいていくか.
(有名問題)

答え
$1:\dfrac{1+\sqrt 5}{2}$ (約 $1:1.61803$).
解説
最初の正方形の $1$ 辺の長さを $1$ とし, $n$ 個目の正方形の $1$ 辺の長さを $F_n$ とおく.
このとき, $n$ 個目まで正方形を貼り合わせてできる長方形の隣り合う $2$ 辺の長さは $F_n,$ $F_{n+1}$ になる.
\[ F_1 = F_2 = 1\]
であり, $n+2$ 個目の正方形の $1$ 辺の長さは $n+1$ 個目と $n$ 個目の正方形の $1$ 辺の長さの和に等しいから,
\[ F_{n+2} = F_n+F_{n+1}\]
が成り立ち, 数列 $\{ F_n\}$ の一般項は
\[ F_n = \frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^n-\left(\frac{1-\sqrt 5}{2}\right) ^n\right\}\]
である (こちらを参照, $F_n = a_{n-1}$).
$\alpha = \dfrac{1+\sqrt 5}{2},$ $\beta = \dfrac{1-\sqrt 5}{2}$ とおくと
\[\left|\frac{\beta}{\alpha}\right| = \frac{\sqrt 5-1}{\sqrt 5+1} < 1\] となるから,
\[\begin{aligned}
\lim\limits_{n \to \infty}\frac{F_{n+1}}{F_n} &= \lim\limits_{n \to \infty}\frac{\alpha ^{n+1}-\beta ^{n+1}}{\alpha ^n-\beta ^n} = \lim\limits_{n \to \infty}\frac{\alpha -\beta\left(\dfrac{\beta}{\alpha}\right) ^n}{1-\left(\dfrac{\beta}{\alpha}\right) ^n} \\
&= \frac{\alpha -\beta\cdot 0}{1-0} = \alpha
\end{aligned}\]
であり, 求める比の極限値は
\[ 1:\frac{1+\sqrt 5}{2}\]
である.
参考
- 初期条件 $F_1 = F_2 = 1$ と漸化式 $F_{n+2} = F_n+F_{n+1}$ で定まる数列 \[\{ F_n\}:1,1,2,3,5,8,13,21,34,55,89,144,\cdots\] を「フィボナッチ数列」(Fibonacci sequence) と呼ぶ. この数列の項は「フィボナッチ数」と呼ばれ, 花びらの枚数, 植物の種が並んでできるらせんの本数など, 自然界でよく見られる整数である.
- 公式 \[ F_n = \frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^n-\left(\frac{1-\sqrt 5}{2}\right) ^n\right\}\] は「ビネの公式」(Binet's formula) として知られている.
- 「黄金比」(golden ratio) と呼ばれる比 $1:\dfrac{1+\sqrt 5}{2}$ は最も美しい比であると言われ, 多くの美術作品の中にこの比を見ることができる.
クイズ《らせん状に並べられた正三角形》
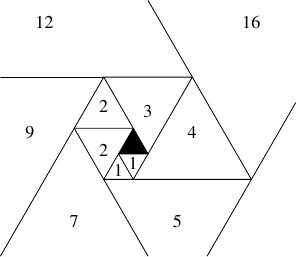
図のように黒塗りの正三角形の周りに正三角形をらせん状に並べていくとき, 正三角形とその直前に並べられた正三角形の辺の長さの比はどのような値に近づいていくか.
極限値が存在することは証明なしに認めてよい.
ヒント: $\omega$ を $1$ の虚数立方根とするとき $(x-u-v)(x-u\omega -v\omega ^2)(x-u\omega ^2-v\omega ) = x^3-3uvx-u^3-v^3$ が成り立つことを利用する.
(有名問題)

答え
$\displaystyle 1:\sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}+\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}.$
解説
黒塗りの正三角形の $1$ 辺の長さを $1$ とし, $n$ 番目に並べられた白塗りの正三角形の $1$ 辺の長さを $P_n$ とおく.
このとき,
\[ P_1 = P_2 = 1,\ P_3 = 2, \quad P_{n+3} = P_n+P_{n+1}\]
が成り立つ.
数列 $\left\{\dfrac{P_{n+1}}{P_n}\right\}$ が $x$ に収束する (証明は省略) とすると,
\[\frac{P_{n+3}}{P_{n+2}}\cdot\frac{P_{n+2}}{P_{n+1}}\cdot\frac{P_{n+1}}{P_n} = \frac{P_{n+3}}{P_n} = 1+\frac{P_{n+1}}{P_n}\]
から,
となる.
この $3$ 次方程式の実数解を求めればよい.
$x = u+v$ とし, $\omega$ を $1$ の虚数立方根とする.
このとき
\[ (x-u-v)(x-u\omega -v\omega ^2)(x-u\omega ^2-v\omega ) = x^3-3uvx-u^3-v^3\]
が成り立つから, 右辺と $x^3-x-1$ を比較すると
\[ -3uv = -1, \quad -u^3-v^3 = -1\]
よって
\[ u^3+v^3 = 1, \quad u^3v^3 = \frac{1}{27}\]
が得られる.
これは $u^3,$ $v^3$ が $2$ 次方程式
\[ t^2-t+\dfrac{1}{27} = 0\]
の解であることを意味するから, $u^3 = \dfrac{1}{2}+\dfrac{1}{6}\sqrt{\dfrac{23}{3}},$ $v^3 = \dfrac{1}{2}-\dfrac{1}{6}\sqrt{\dfrac{23}{3}}$ とすると,
\[\begin{aligned}
u &= \sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}\omega ^k \quad (k = 0,1,2), \\
v &= \sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}\omega ^l \quad (l = 0,1,2)
\end{aligned}\]
となる.
この $u,$ $v$ は $u^3+v^3 = 1$ を満たす.
\[\begin{aligned}
uv &= \sqrt[3]{\left(\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}\right)\left(\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}\right)}\omega ^{k+l} \\
&= \sqrt[3]{\frac{1}{4}-\frac{23}{4\cdot 27}}\omega ^{k+l} = \sqrt[3]{\frac{1}{27}}\omega ^{k+l} = \frac{1}{3}\omega ^{k+l}
\end{aligned}\]
から, $3uv = 1$ となるのは $(k,l) = (0,0),$ $(1,2),$ $(2,1)$ の場合に限る.
上記の等式により, これらの場合に $x = u+v$ は $[1]$ の解になる.
$3$ 次方程式の解は $3$ つしかないから, $[1]$ の解は
\[\begin{aligned}
x = &\sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}+\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}, \\
&\sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}\omega +\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}\omega ^2, \\
&\sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}\omega ^2+\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}\omega
\end{aligned}\]
と表される.
ゆえに, 正三角形とその直前に並べられた正三角形の辺の長さの比は
\[ 1:\sqrt[3]{\frac{1}{2}+\frac{1}{6}\sqrt{\frac{23}{3}}}+\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}\]
に近づいていく.
| $x^3 = 1+x$ つまり $x^3-x-1 = 0 \quad \cdots [1]$ |
クイズ《くじで当たらない確率の極限値》
$n$ 本中 $1$ 本だけ当たりが入ったくじを $n$ 回引くときに $1$ 回も当たらない確率は, $n$ が大きくなるにつれてどのような値に近づいていくか.
ただし, 引いたくじは毎回もとに戻すものとする.
(有名問題)
答え
$\dfrac{1}{e}$ ($e$: ネイピア数).
解説
このくじにおいて, 当たりの確率は $\dfrac{1}{n},$ はずれの確率は $1-\dfrac{1}{n}$ であるから, $n$ 回引くときに $1$ 回も当たらない確率は
\[\begin{aligned}
\left( 1-\frac{1}{n}\right)^n &= \frac{1}{\left( 1+\dfrac{1}{-n}\right)^{-n}} \\
&\to \frac{1}{e} \quad (n \to \infty)
\end{aligned}\]
である.
ここで,
\[ e = \lim\limits_{k \to 0}(1+k)^{\frac{1}{k}} = \lim\limits_{x \to \pm\infty}\left( 1+\frac{1}{x}\right) ^x\]
であることを使った.
参考
答えの近似値は,
\[\frac{1}{e} = 0.3678794411\cdots\]
である.
無限級数
クイズ《硬貨を投げる回数の期待値》
表が出る確率も裏が出る確率も $\dfrac{1}{2}$ である硬貨を表が出るまで投げ続けるとき, 何回目に投げ終わると見込まれるか.
(有名問題)
答え
$2$ 回目.
解説
$n$ 回目に初めて表が出る確率を $p_n$ とおく.
求める期待値 $E$ は
\[ E = \sum_{n = 1}^\infty np_n\]
と表される.
- (1)
- $p_n$ を求める. $n$ 回目に初めて表が出るのは, $n-1$ 回目までに裏が出て $n$ 回に表が出る場合であるから, その確率は \[ p_n = \left(\frac{1}{2}\right) ^{n-1}\cdot\frac{1}{2} = \left(\frac{1}{2}\right) ^n\] である.
- (2)
- $S_n = \displaystyle\sum_{k = 1}^nkp_k$ を求める. (1) の結果から, \[ S_n = 1\cdot\frac{1}{2}+2\cdot\left(\frac{1}{2}\right) ^2+\cdots +n\cdot\left(\frac{1}{2}\right) ^n\] である. 両辺に $\dfrac{1}{2}$ を掛けると \[\frac{1}{2}S_n = 1\cdot\left(\frac{1}{2}\right) ^2+\cdots +(n-1)\cdot\left(\frac{1}{2}\right) ^n+n\cdot\left(\frac{1}{2}\right) ^{n+1}\] となるから, 辺々を引くと \[\begin{aligned} \frac{1}{2}S_n &= \frac{1}{2}+\left(\frac{1}{2}\right) ^2+\cdots +\left(\frac{1}{2}\right) ^n-n\cdot\left(\frac{1}{2}\right) ^{n+1} \\ &= \frac{\dfrac{1}{2}\left\{ 1-\left(\dfrac{1}{2}\right) ^n\right\}}{1-\dfrac{1}{2}}-n\cdot\left(\frac{1}{2}\right) ^{n+1} \\ &= 1-\left(\frac{1}{2}\right) ^n-n\cdot\left(\frac{1}{2}\right) ^{n+1} \\ S_n &= 2-2\cdot\left(\frac{1}{2}\right) ^n-2n\cdot\left(\frac{1}{2}\right) ^{n+1} \end{aligned}\] が得られる.
- (3)
- $E$ の値を求める. (2) の結果から, \[\begin{aligned} E &= \lim_{n \to \infty}S_n \\ &= \lim_{n \to \infty}\left\{ 2-2\cdot\left(\frac{1}{2}\right) ^n-2n\cdot\left(\frac{1}{2}\right) ^{n+1}\right\} \\ &= 2 \end{aligned}\] である.
クイズ《労働者の報酬》
- (1)
- $1$ 日目に $1$ 人の労働者がおり, $n$ 日目 $(n \geqq 2)$ に $n$ 人の労働者が増える. 毎日 $a$ 円の報酬を労働者全員で均等割りするとして無限に働き続けるとき, $1$ 日目からいる労働者が得られる報酬は合わせて何円か.
- (2)
- $1$ 日目に $1$ 人の雇用人がおり, $n$ 日目 $(n \geqq 2)$ に $2n-1$ 人の労働者が増える. 毎日 $a$ 円の報酬を労働者全員で均等割りするとして無限に働き続けるとき, $2$ 日目からいる労働者が得られる報酬は合わせて何円か.
(有名問題, 脚色あり)
答え
- (1)
- $2a$ 円.
- (2)
- $\dfrac{3}{4}a$ 円.
解説
- (1)
- $n$ 日目に労働者は
いるから, $n$ 日目の報酬は$\displaystyle\sum_{k = 1}^nk = \frac{n(n+1)}{2}$ (人)
である. よって, $1$ 日目からいる労働者が $N$ 日目までに得られる報酬は \[\sum_{n = 1}^N\frac{2a}{n(n+1)} = 2a\sum_{n = 1}^N\left(\frac{1}{n}-\frac{1}{n+1}\right) = 2a\left( 1-\frac{1}{N+1}\right)\] (円) であるから, $\displaystyle\lim\limits_{N \to \infty}\dfrac{1}{N+1} = 0$ により, この労働者が無限に働き続けるときに得られる報酬は$\displaystyle a\div\frac{n(n+1)}{2} = \frac{2a}{n(n+1)}$ (円)
である.$2a$ 円 - (2)
- $n$ 日目 $(n \geqq 2)$ に労働者は
いるから, $n$ 日目の報酬は$\displaystyle\sum_{k = 2}^n(2k-1) = \displaystyle\sum_{k = 1}^n(2k-1)-1 = n^2-1$ (人)
である. よって, $2$ 日目からいる労働者が $N$ 日目までに得られる報酬は \[\begin{aligned} \sum_{n = 2}^N\frac{a}{(n+1)(n-1)} &= \frac{a}{2}\sum_{n = 2}^N\left(\frac{1}{n-1}-\frac{1}{n+1}\right) \\ &= \frac{a}{2}\left( 1+\frac{1}{2}-\frac{1}{N}-\frac{1}{N+1}\right) \end{aligned}\] (円) であるから, $\displaystyle\lim\limits_{N \to \infty}\dfrac{1}{N} = \lim\limits_{N \to \infty}\dfrac{1}{N+1} = 0$ により, この労働者が無限に働き続けるときに得られる報酬は$a\div (n^2-1) = \dfrac{a}{(n+1)(n-1)}$ (円)
である.$\dfrac{3}{4}a$ 円
参考
- $T_n = \dfrac{n(n+1)}{2}$ ($n$: 正の整数) の形の整数を「三角数」と呼ぶ.
- 「三角数」の逆数の総和 $\displaystyle\sum_{n = 1}^\infty\frac{1}{T_n} = 2$ はメンゴーリによって求められた.
- ヤコブ・ベルヌーイ, ヨハン・ベルヌーイは, 平方数の逆数の総和 $\sum_{n = 1}^\infty\frac{1}{n^2}$ の値を問う「バーゼル問題」を解けなかったため, その代わりに無限級数 $\sum_{n = 2}^\infty\frac{1}{n^2-1}$ の和を求めた.
クイズ《元気な犬が走った道のり》
主人が犬を連れて家に帰る途中, 家から $a$ m の地点に来たとき, 犬は先に家に向かって走り出し, 家に着くとすぐに引き返して主人の元へ戻ってきた.
すると, またすぐに家に向かって走り出し, 家に着くとすぐに引き返して主人の元へ戻る.
犬は, 主人が歩く速さの $r$ 倍の速さで, 主人が家に着くまで, このような往復運動を繰り返す.
犬が $n$ 回目に家に向かって走り出したときの家までの道のりは何 m か.
また, 主人が家に着くまでに犬は何 m 走るか.
(有名問題)
答え
$a\left(\dfrac{r-1}{r+1}\right) ^n$ m, $ar$ m.
解説
犬が $n$ 回目 $(n \geqq 0)$ に家に向かって走り出したときの家までの道のりを $a_n$ m とおく.
- (1)
- 犬が $n$ 回目に家に向かって走り出したときから $n+1$ 回目に家に向かって走り出すまでに走る道のりについて
\[ a_n+a_{n+1} = r(a_n-a_{n+1})\]
が成り立つから,
である. よって, 犬が $n$ 回目に家に向かって走り出したときの家までの道のりは$(r+1)a_{n+1} = (r-1)a_n$ つまり $a_{n+1} = \dfrac{r-1}{r+1}a_n$
である.$a_n = a\left(\dfrac{r-1}{r+1}\right) ^n$ (m) - (2)
- また,
\[\begin{aligned}
a_n+a_{n+1} &= a\left(\dfrac{r-1}{r+1}\right) ^n+a\left(\dfrac{r-1}{r+1}\right) ^{n+1} \\
&= a\left(\dfrac{r-1}{r+1}\right) ^n\left( 1+\frac{r-1}{r+1}\right) \\
&= \frac{2ar}{r+1}\left(\dfrac{r-1}{r+1}\right) ^n
\end{aligned}\]
であるから, 主人が家に着くまでに犬が走った道のりは
である.$\displaystyle\sum_{n = 0}^\infty (a_n+a_{n+1}) = \frac{2ar}{r+1}\cdot\frac{1}{1-\dfrac{r-1}{r+1}} = ar$ (m)
無限積
クイズ《ヴィエトの公式の幾何学的意味》
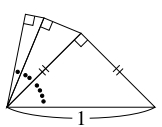
斜辺の長さが $1$ の直角二等辺三角形を $1$ 個目の直角三角形として, 直角三角形の大きい方の鋭角の対辺と $1$ 辺を共有する直角三角形を作るという操作を, 小さい方の鋭角の大きさが毎回半減するように続けていく.
このとき, 新たに作られる直角三角形の斜辺の長さはどのような値に近づいていくか.

(有名問題, 脚色あり)
答え
$\dfrac{2}{\pi}.$
解説
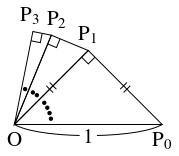
直角三角形 $\mathrm{OP}_0\mathrm P_1,$ $\cdots,$ $\mathrm{OP}_{n-1}\mathrm P_n,$ $\cdots$ を
\[\begin{aligned}
&\mathrm{OP}_0 = 1, \quad \angle\mathrm P_0\mathrm{OP}_1 = \frac{\pi}{4}, \\
&\angle\mathrm P_n\mathrm{OP}_{n+1} = \frac{1}{2}\angle\mathrm P_{n-1}\mathrm{OP}_n
\end{aligned}\]
となるように定める.
 このとき,
\[\mathrm{OP}_n = \mathrm{OP}_{n-1}\cos\frac{\pi}{2^{n+1}} \quad (n \geqq 1)\]
であるから,
\[\mathrm{OP}_n = \cos\frac{\pi}{4}\cdots\cos\frac{\pi}{2^{n+1}} \quad \cdots [1]\]
である.
倍角の公式により
\[\cos\frac{\theta}{2^k}\sin\frac{\theta}{2^k} = \frac{1}{2}\cos\frac{\theta}{2^{k-1}}\]
であるから,
\[\begin{aligned}
\cos\frac{\pi}{4}\cdots\cos\frac{\pi}{2^{n+1}}\sin\frac{\pi}{2^{n+1}} &= \frac{1}{2}\cos\frac{\pi}{4}\cdots\cos\frac{\pi}{2^n}\sin\frac{\pi}{2^n} \\
&= \cdots \\
&= \frac{1}{2^{n-1}}\cos\frac{\pi}{4}\sin\frac{\pi}{4} \\
&= \frac{1}{2^n}\sin\frac{\pi}{2} \\
&= \frac{1}{2^n} \quad \cdots [2]
\end{aligned}\]
が成り立つ.
よって, $[1],$ $[2]$ から,
\[\begin{aligned}
\mathrm{OP}_n &= \frac{1}{2^n}\div\sin\frac{\pi}{2^{n+1}} \\
&= \frac{2}{\pi}\cdot\frac{\pi}{2^{n+1}}\div\sin\frac{\pi}{2^{n+1}} \\
&\to \frac{2}{\pi}\cdot 1 = \frac{2}{\pi} \quad (n \to \infty )
\end{aligned}\]
が成り立つ.
ゆえに, 求める極限値は
\[\lim\limits_{n \to \infty}\mathrm{OP}_{n-1} = \frac{2}{\pi}\]
である.
このとき,
\[\mathrm{OP}_n = \mathrm{OP}_{n-1}\cos\frac{\pi}{2^{n+1}} \quad (n \geqq 1)\]
であるから,
\[\mathrm{OP}_n = \cos\frac{\pi}{4}\cdots\cos\frac{\pi}{2^{n+1}} \quad \cdots [1]\]
である.
倍角の公式により
\[\cos\frac{\theta}{2^k}\sin\frac{\theta}{2^k} = \frac{1}{2}\cos\frac{\theta}{2^{k-1}}\]
であるから,
\[\begin{aligned}
\cos\frac{\pi}{4}\cdots\cos\frac{\pi}{2^{n+1}}\sin\frac{\pi}{2^{n+1}} &= \frac{1}{2}\cos\frac{\pi}{4}\cdots\cos\frac{\pi}{2^n}\sin\frac{\pi}{2^n} \\
&= \cdots \\
&= \frac{1}{2^{n-1}}\cos\frac{\pi}{4}\sin\frac{\pi}{4} \\
&= \frac{1}{2^n}\sin\frac{\pi}{2} \\
&= \frac{1}{2^n} \quad \cdots [2]
\end{aligned}\]
が成り立つ.
よって, $[1],$ $[2]$ から,
\[\begin{aligned}
\mathrm{OP}_n &= \frac{1}{2^n}\div\sin\frac{\pi}{2^{n+1}} \\
&= \frac{2}{\pi}\cdot\frac{\pi}{2^{n+1}}\div\sin\frac{\pi}{2^{n+1}} \\
&\to \frac{2}{\pi}\cdot 1 = \frac{2}{\pi} \quad (n \to \infty )
\end{aligned}\]
が成り立つ.
ゆえに, 求める極限値は
\[\lim\limits_{n \to \infty}\mathrm{OP}_{n-1} = \frac{2}{\pi}\]
である.

参考
半角の公式 $\cos ^2\dfrac{\theta}{2} = \dfrac{1+\cos\theta}{2}$ により
\[\begin{aligned}
\cos\frac{\pi}{4} &= \frac{\sqrt 2}{2}, \\
\cos\frac{\pi}{8} &= \sqrt{\frac{1+\dfrac{\sqrt 2}{2}}{2}} = \frac{\sqrt{2+\sqrt 2}}{2}, \\
\cos\frac{\pi}{16} &= \sqrt{\frac{1+\dfrac{\sqrt{2+\sqrt 2}}{2}}{2}} = \frac{\sqrt{2+\sqrt{2+\sqrt 2}}}{2},\ \cdots
\end{aligned}\]
であるから, 上記の計算により
\[\frac{2}{\pi} = \cdot\frac{\sqrt 2}{2}\cdot\frac{\sqrt{2+\sqrt 2}}{2}\cdot\frac{\sqrt{2+\sqrt{2+\sqrt 2}}}{2}\cdot\cdots\]
が成り立つ.
これは, 「ヴィエトの公式」(Viète's formula) として知られており ($1593$ 年),
$\pi$ が現れる無限和または無限積の公式としてはヨーロッパで初めて発見されたものである.
それ以前には, $\tan x$ の逆関数 $\mathrm{arctan}\,x$ の展開公式 $\mathrm{arctan}\,x = \sum\limits_{n = 0}^\infty\dfrac{(-1)^n}{2n+1}x^{2n+1}$ $(-1 \leqq x \leqq 1)$ がインドのケーララ学派の間で知られていたため,
この種の公式としては $\dfrac{\pi}{4} = \sum\limits_{n = 0}^\infty\dfrac{(-1)^n}{2n+1}$ が最も古いと考えられている.
関数の極限
クイズ《半円形の鏡による光の反射》
円柱を縦に $2$ 等分した形の鏡張りの部屋の隅 $\mathrm A$ から曲面の壁に向かって水平に光を発射する.
その発射方向を部屋のもう一方の隅 $\mathrm B$ に近づけていくとき, 反射した光が平面の壁に当たる点 $\mathrm P$ と部屋の隅との距離の比 $\mathrm{AP}:\mathrm{BP}$ はどのような値に近づいていくか.
ただし, この部屋では, 曲面の壁と平面の壁が交差する部分を部屋の隅と呼ぶ.
(有名問題)
答え
$2:1.$
解説
円の半径が $1$ であるとしても一般性を失わない.
このとき, 円の中心を $\mathrm O,$ 光が反射する点を $\mathrm R$ とおき, $\theta = \angle\mathrm{OAR}$ とおく.
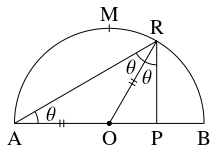 反射角は入射角に等しいことと $\mathrm{OR} = \mathrm{OA}$ から
\[\angle\mathrm{ORP} = \angle\mathrm{ORA} = \theta\]
であるので,
\[\angle\mathrm{OPR} = \pi -3\theta\]
が成り立つ.
よって, $\triangle\mathrm{OPR}$ に正弦定理を適用すると,
\[\frac{\mathrm{OP}}{\sin\theta} = \frac{1}{\sin (\pi -3\theta )} = \frac{1}{\sin 3\theta}\]
が得られる.
点 $\mathrm R$ を点 $\mathrm B$ に限りなく近づけていくとき, 点 $\mathrm P$ が近づいていく点を $\mathrm P_0$ とすると, $\theta \to +0$ であるから,
\[\begin{aligned}
\mathrm{OP}_0 &= \lim_{\theta \to +0}\mathrm{OP} = \lim_{\theta \to +0}\frac{\sin\theta}{\sin 3\theta} = \frac{1}{3}\lim_{\theta \to +0}\frac{\sin\theta}{\theta}\cdot\frac{3\theta}{\sin 3\theta} \\
&= \frac{1}{3}\cdot 1\cdot\frac{1}{1} = \frac{1}{3}
\end{aligned}\]
となる.
よって, 求める距離の比は
\[\mathrm{AP}_0:\mathrm P_0\mathrm B = \left( 1+\frac{1}{3}\right) :\left( 1-\frac{1}{3}\right) = 2:1\]
である.
反射角は入射角に等しいことと $\mathrm{OR} = \mathrm{OA}$ から
\[\angle\mathrm{ORP} = \angle\mathrm{ORA} = \theta\]
であるので,
\[\angle\mathrm{OPR} = \pi -3\theta\]
が成り立つ.
よって, $\triangle\mathrm{OPR}$ に正弦定理を適用すると,
\[\frac{\mathrm{OP}}{\sin\theta} = \frac{1}{\sin (\pi -3\theta )} = \frac{1}{\sin 3\theta}\]
が得られる.
点 $\mathrm R$ を点 $\mathrm B$ に限りなく近づけていくとき, 点 $\mathrm P$ が近づいていく点を $\mathrm P_0$ とすると, $\theta \to +0$ であるから,
\[\begin{aligned}
\mathrm{OP}_0 &= \lim_{\theta \to +0}\mathrm{OP} = \lim_{\theta \to +0}\frac{\sin\theta}{\sin 3\theta} = \frac{1}{3}\lim_{\theta \to +0}\frac{\sin\theta}{\theta}\cdot\frac{3\theta}{\sin 3\theta} \\
&= \frac{1}{3}\cdot 1\cdot\frac{1}{1} = \frac{1}{3}
\end{aligned}\]
となる.
よって, 求める距離の比は
\[\mathrm{AP}_0:\mathrm P_0\mathrm B = \left( 1+\frac{1}{3}\right) :\left( 1-\frac{1}{3}\right) = 2:1\]
である.
