本格数学クイズ (方程式論)
方程式論
クイズ《黄金長方形と超黄金長方形》
短辺の長さがともに $1$ である「黄金長方形」,「超黄金長方形」のキャンバスが $1$ 枚ずつある.
$1$ 本につき面積 $1$ の領域が塗れる絵の具でこれらのキャンバスを塗るとき, 何本の絵の具が必要か, 整数で答えよ.
ただし,「黄金長方形」とは, 端から最大の正方形を取り除いて得られる長方形が, もとの長方形と相似になる長方形のことである. また,「超黄金長方形」とは, $1$ 本の対角線が消えるように, 端から最大の正方形, 最小の長方形を順に取り除いて得られる長方形が, もとの長方形と相似になる長方形のことである.
ただし,「黄金長方形」とは, 端から最大の正方形を取り除いて得られる長方形が, もとの長方形と相似になる長方形のことである. また,「超黄金長方形」とは, $1$ 本の対角線が消えるように, 端から最大の正方形, 最小の長方形を順に取り除いて得られる長方形が, もとの長方形と相似になる長方形のことである.
(有名問題, 脚色あり)
答え
$4$ 本.
解説
- (1)
- 「黄金長方形」のキャンバスの面積を評価する.
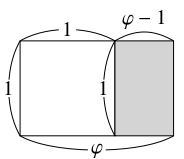
短辺の長さが $1$ である「黄金長方形」の長辺の長さを $\varphi$ とおく.
このキャンバスの面積は $\varphi$ である.
また, 端から最大の正方形を取り除いて得られる長方形の短辺の長さは $\varphi -1,$ 長辺の長さは $1$ である.
よって, 相似比により \[ 1:\varphi = (\varphi -1):1\] つまり \[\begin{aligned} \varphi (\varphi -1) &= 1 \\ \varphi ^2-\varphi-1 &= 0 \end{aligned}\] が成り立ち, $\varphi > 0$ から \[\varphi = \frac{1+\sqrt 5}{2} \quad \left(\because\frac{1-\sqrt 5}{2} < 0\right)\] である. したがって, $\varphi$ は $2$ 次関数 $y = x^2-x-1$ のグラフと $x$ 軸の正の部分との交点 ($1$ 個しかない) の $x$ 座標であり, \[\begin{aligned} 1.6^2-1.6-1 &= -0.04 < 0, \\ 1.7^2-1.7-1 &= 0.19 > 0 \end{aligned}\] であるから, \[ 1.6 < \varphi < 1.7\] である.
- (2)
- 「超黄金長方形」のキャンバスの面積を評価する.
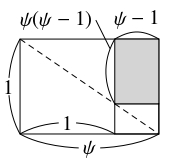
短辺の長さが $1$ である「超黄金長方形」の長辺の長さを $\psi$ とおく.
このキャンバスの面積は $\psi$ である.
また, $1$ 本の対角線が消えるように, 端から最大の正方形, 最小の長方形を順に取り除いて得られる長方形の短辺の長さは $\psi -1,$ 長辺の長さは $\psi (\psi -1)$ である (相似比を利用した).
よって, 取り除く正方形がもとの長方形の対角線から切り取る線分の長さは \[\frac{1}{\psi}\sqrt{1+\psi ^2} = \sqrt{1+\{\psi (\psi -1)\} ^2}\] と $2$ 通りに表される. 分母を払って両辺を $2$ 乗すると \[ 1+\psi ^2 = \psi ^2\{ 1+\psi ^2(\psi -1)^2\}\] となるから, 展開して整理すると \[\psi ^6-2\psi ^5+\psi ^4 -1 = 0\] となり, 左辺を因数分解すると \[ (\psi ^3-\psi ^2+1)(\psi ^3-\psi ^2-1) = 0\] が得られる. $3$ 次関数 $y = x^3-x^2+1$ のグラフを描くと $x$ 軸の正の部分と共有点をもたないことがわかるから, $\psi$ は $y = x^3-x^2-1$ のグラフと $x$ 軸の交点 ($1$ 個しかない) の $x$ 座標である (定数項の符号に注意).
さらに \[\begin{aligned} 1.4^3-1.4^2-1 &= -0.216 < 0, \\ 1.5^3-1.5^2-1 &= 0.125 > 0 \end{aligned}\] であるから, 中間値の定理により \[ 1.4 < \psi < 1.5\] である.
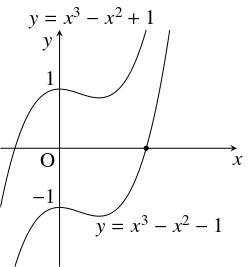
- (3)
- (1), (2) から
\[ 3 = 1.6+1.4 < \varphi +\psi < 1.7+1.5 = 3.2\]
であるので, 必要な絵の具は
である.$4\div 1 = 4$ (本)
参考
- $x^2-x-1 = 0$ の正の解 \[\varphi = \dfrac{1+\sqrt 5}{2} = 1.6180339887\cdots\] を「黄金数」(golden number) と呼ぶ. また, 比 $1:\varphi$ を「黄金比」(golden ratio) と呼び, 短辺と長辺の長さの比が「黄金比」である長方形を「黄金長方形」(golden rectangle) と呼ぶ.
- $x^3-x^2-1 = 0$ の唯一の実数解 \[\psi = \dfrac{1}{\sqrt[3]{\dfrac{1}{2}+\dfrac{1}{6}\sqrt{\dfrac{31}{3}}}+\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{6}\sqrt{\dfrac{31}{3}}}} = 1.4655712318\cdots\] を「超黄金数」(supergolden number) と呼ぶ. また, 比 $1:\psi$ を「超黄金比」(supergolden ratio) と呼び, 短辺と長辺の長さの比が「超黄金比」である長方形を「超黄金長方形」(supergolden rectangle) と呼ぶ.
クイズ《カラビの三角形》
$\angle\mathrm A$ が鈍角である二等辺三角形 $\mathrm{ABC}$ と, 互いに合同な $2$ つの正方形 $\mathrm{PQRS},$ $\mathrm{ATUV}$ があり, 頂点 $\mathrm P,$ $\mathrm T$ は辺 $\mathrm{AB}$ 上に, 辺 $\mathrm{QR}$ と頂点 $\mathrm U$ は辺 $\mathrm{BC}$ 上に, 頂点 $\mathrm S$ は辺 $\mathrm{AC}$ 上にあるとする.
$\triangle\mathrm{ABC}$ の等辺に対する底辺の長さの比はある $3$ 次方程式を満たす.
その $3$ 次方程式を求めよ.
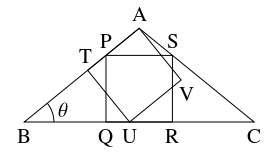(ヒント: $\mathrm{AB} = \mathrm{AC} = 1$ とし, $x = \mathrm{BC},$ $y = \mathrm{AP},$ $\angle\mathrm{ABC} = \theta$ とおく.
まず, 正方形 $\mathrm{PQRS}$ に着目することで, $\cos\theta,$ $\sin\theta$ を用いて $x,$ $y$ を表す式を導く.
次に, 正方形 $\mathrm{ATUV}$ に着目することで, $\cos\theta,$ $\sin\theta$ を用いて $y$ を表す式を導く.)
(有名問題)
答え
$2x^3-2x^2-3x+2 = 0.$
解説
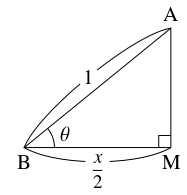
$\mathrm{AB} = \mathrm{AC} = 1$ とし, $x = \mathrm{BC},$ $y = \mathrm{AP},$ $\angle\mathrm{ABC} = \theta$ とおく.
さらに, 正方形 $\mathrm{PQRS},$ $\mathrm{ATUV}$ の $1$ 辺の長さを $l$ とおく.
- (1)
- 点 $\mathrm A$ から $\mathrm{BC},$ $\mathrm{PS}$ に下ろした垂線の足をそれぞれ $\mathrm M,$ $\mathrm N$ とおく.
直角三角形 $\mathrm{ABM}$ に着目すると
\[ x = 2\cos\theta \quad \cdots [1]\]
が得られる.
直角三角形 $\mathrm{APN},$ $\mathrm{PBQ}$ に着目すると \[ l = 2y\cos\theta = (1-y)\sin\theta \quad \cdots [2]\] から \[ y = \frac{\sin\theta}{\sin\theta + 2\cos\theta} \quad \cdots [3]\] が得られる.
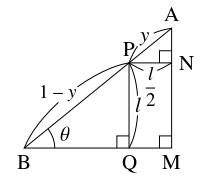
- (2)
- 直角三角形 $\mathrm{UBT}$ に着目すると, $[2]$ から
\[\tan\theta = \frac{l}{1-l} = \frac{2y\cos\theta}{1-2y\cos\theta},\]
よって
\[\begin{aligned}
\tan\theta (1-2y\cos\theta ) &= 2y\cos\theta \\
\tan\theta -2y\sin\theta &= 2y\cos\theta,
\end{aligned}\]
つまり
\[ y = \frac{\tan\theta}{2(\sin\theta +\cos\theta )} = \frac{\sin\theta}{2\cos\theta (\sin\theta +\cos\theta )} \quad \cdots [4]\]
が得られる.
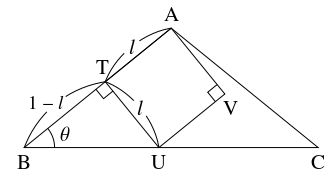
- (3)
- $[2],$ $[4]$ から \[\begin{aligned} \frac{\sin\theta}{\sin\theta + 2\cos\theta} &= \frac{\sin\theta}{2\cos\theta (\sin\theta +\cos\theta )} \\ 2\cos\theta (\sin\theta +\cos\theta ) &= \sin\theta + 2\cos\theta \quad (\because\sin\theta \neq 0) \end{aligned}\] が得られ, 整理した \[\sin\theta (2\cos\theta -1) = 2\cos\theta (1-\cos\theta )\] の両辺を $2$ 乗すると $\cos ^2\theta +\sin ^2\theta = 1$ から \[ (1-\cos ^2\theta )(2\cos\theta -1)^2 = 4\cos ^2\theta (1-\cos\theta )^2\] が得られる. $[1]$ から $\cos\theta = \dfrac{x}{2}$ であるので, \[\begin{aligned} \left( 1-\frac{x^2}{4}\right) (x-1)^2 &= x^2\left( 1-\frac{x}{2}\right) ^2 \\ (4-x^2)(x-1)^2 &= x^2(2-x)^2 \\ \end{aligned}\] つまり \[\begin{aligned} x^2(2-x)^2+(x^2-4)(x-1)^2 &= 0 \\ x^2(x-2)^2+(x+2)(x-2)(x-1)^2 &= 0 \\ (x-2)\{ x^2(x-2)+(x+2)(x-1)^2\} &= 0 \\ (x-2)\{ x^2(x-2)+(x+2)(x^2-2x+1)\} &= 0 \\ (x-2)(2x^3-2x^2-3x+2) &= 0 \\ \end{aligned}\] であり, 三角形の成立条件により $x \neq 2$ であることから \[ 2x^3-2x^2-3x+2 = 0\] である.
参考
- 正三角形の他に, 内接する最大の正方形が $3$ 通りの方法で配置できるような三角形 (鈍角二等辺三角形) がただ $1$ つ存在する.
この三角形を「カラビの三角形」(Calabi's triangle) と呼ぶ.
上記の問題の三角形は, 二等辺三角形の対称性により内接する最大の正方形が $3$ 通りの方法で配置できるから,「カラビの三角形」である.
- 「カラビの三角形」における等辺に対する底辺の長さの比 $x$ は, $3$ 次方程式 \[ 2x^3-2x^2-3x+2 = 0\] の $3$ つの実数解のうち最大の解であり,「カルダーノの公式」(こちらを参照) により \[ x = \frac{1}{3}\left( 1+\sqrt[3]{-\frac{23}{4}+\frac{3}{4}\sqrt{237}i}+\sqrt[3]{-\frac{23}{4}-\frac{3}{4}\sqrt{237}i}\right)\] と表され,「カラビの三角形定数」と呼ばれる. その近似値は \[ x = 1.55138\cdots\] であり (こちらを参照),「カラビの三角形」の鋭角, 鈍角の大きさの近似値はそれぞれ \[ 39.13202\cdots ^\circ, \quad 101.73594\cdots ^\circ\] である.
クイズ《奇数次方程式の実数解の存在》
実数係数の奇数次の方程式 $f(x) = 0$ は少なくとも $1$ つの実数解をもつ, という主張は正しいか.
正しければ証明し, 正しくなければ反例を挙げよ.
(有名問題)
答え
正しい (証明は解説を参照).
解説
$n$ を奇数として, 実数係数 $n$ 次多項式 $f(x) = \sum\limits_{k = 0}^na_kx^k$ $(a_n \neq 0)$ を考える.
- (i)
- $a_n > 0$ のとき. $x \to \pm\infty$ のとき, $n$ が奇数であることから \[ a_nx^n \to \pm\infty, \quad \sum_{k = 0}^n\frac{a_k}{a_n}x^{k-n} \to 1\] であり, \[ f(x) = a_nx^n\sum_{k = 0}^n\frac{a_k}{a_n}x^{k-n} \to \pm\infty\] であるから (複号同順), ある実数 $a,$ $b$ $(a < b)$ について \[ f(a) < 0, \quad f(b) > 0\] が成り立つ. よって, 中間値の定理により, $a < x < b$ の範囲に $f(x) = 0$ の実数解が存在する.
- (ii)
- $a_n < 0$ のとき. (i) の結果から $-f(x) = 0$ の実数解が存在するので, $f(x) = 0$ の実数解が存在する.
比
クイズ《合比の理》
昨年, A 部と B 部の人数比は C 部と D 部の人数比と同じであった.
今年は, A 部に昨年の B 部と同じ人数が増え B 部の人数は変わらず, C 部に昨年の D 部と同じ人数が増え, D 部の人数は変わらなかった.
このとき, 今年の A 部と B 部の人数比, C 部と D 部の人数比についてどのようなことが言えるか.
(有名問題, 脚色あり)
答え
今年も A 部と B 部の人数比は C 部と D 部の人数比と同じ.
解説
昨年の A 部, B 部, C 部, D 部の人数をそれぞれ $a$ 人, $b$ 人, $c$ 人, $d$ 人とする.
仮定により
\[\frac{a}{b} = \frac{c}{d}\]
であるから, 両辺に $1$ を加えると
\[\begin{aligned}
\frac{a}{b}+1 &= \frac{c}{d}+1 \\
\frac{a+b}{b} &= \frac{c+d}{d}
\end{aligned}\]
が得られる.
ゆえに, 今年も A 部と B 部の人数比は C 部と D 部の人数比と同じである.
参考
\[\frac{a}{b} = \frac{c}{d} \Longrightarrow \frac{a+b}{b} = \frac{c+d}{d}\]
を「合比の理」と呼ぶ.
\[\frac{a}{b} = \frac{c}{d} \Longrightarrow \frac{a-b}{b} = \frac{c-d}{d}\]
も成り立ち, これを「除比の理」と呼ぶ.