本格数学クイズ (離散幾何学)
平面充填形
クイズ《正平面充填形》
平面に $1$ 種類の正多角形を隙間も重なりもなく敷き詰める方法は, 全部で何通りあるか.
ただし, 使用する正多角形はすべて同じ大きさであり, $3$ 枚以上の正多角形は頂点のみを共有する方法のみを考えるものとする.
(有名問題)
答え
$3$ 通り.
解説
平面に合同な正 $p$ 角形が隙間も重なりもなく敷き詰めて, 各頂点で $q$ 個の正 $p$ 角形の辺が交わるようにできたとする.
$1$ つの頂点に集まる角の和は $360^\circ$ であり, 正 $p$ 角形の内角の大きさは $180^\circ\times (p-2)\div p$ であるから,
\[\frac{180(p-2)q}{p} = 360\]
が成り立つ.
整理すると,
\[\begin{aligned}
(p-2)q &= 2p \\
pq-2p-2q &= 0 \\
(p-2)(q-2) &= 4
\end{aligned}\]
となる.
$p \geqq 3,$ $q \geqq 3$ から $p-2 \geqq 1,$ $q-2 \geqq 1$ であることに注意すると,
\[\begin{aligned}
(p-2,q-2) &= (1,4),\ (2,2),\ (4,1) \\
(p,q) &= (3,6),\ (4,4),\ (6,3)
\end{aligned}\]
が得られる.
正三角形, 正方形, 正六角形はそれぞれ, 次の図のように平面に敷き詰められる.
ゆえに, 平面に $1$ 種類の正多角形を隙間も重なりもなく敷き詰める方法は全部で $3$ 通りある.
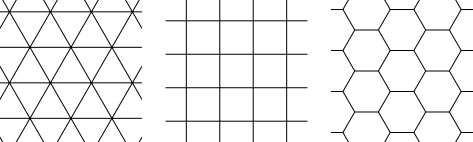

参考
- 有限種類の合同な図形で平面を隙間も重なりもなく敷き詰めることを「平面充填」(tessellation) と呼ぶ. 敷き詰めに使われる平面図形を「タイル」(tile) と呼び,「タイル」で敷き詰められた平面を「平面充填形」(tessellation) と呼ぶ.
- ピタゴラスは, $1$ 種類の正多角形を「タイル」とする「平面充填形」($3$ 枚以上の「タイル」は頂点のみを共有するもの) は正三角形, 正方形, 正六角形を使う $3$ パターンに限ることを証明した. これらの「平面充填形」を「正平面充填形」(regular tessellation) と呼ぶ.
グラフ理論
クイズ《一筆書きが可能な正多面体》
正多面体のうち, すべての辺が一筆書きでなぞれるものはどれか.
(有名問題)
答え
正八面体.
解説
オイラーの定理により, すべての辺をなぞる一筆書きができるためには, 各頂点に集まる辺の本数が偶数でなければならない,
各頂点に集まる辺の本数は, 正四面体が $3,$ 正六面体が $3,$ 正八面体が $4,$ 正十二面体が $3,$ 正二十面体が $5$ であるから, 条件を満たすのは正八面体のみである.
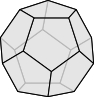
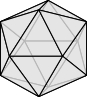





クイズ《正方形の頂点を結ぶ最短経路》
分岐点を新たに設けてもよいとするとき, 正方形の $4$ 個の頂点を結ぶ最短経路の長さは正方形の周の長さの何倍か.
(有名問題)
答え
$\dfrac{1+\sqrt 3}{4}$ 倍 (約 $0.68301$ 倍).
解説
$xy$ 平面上で $4$ 点 $\mathrm A(1,1),$ $\mathrm B(−1,1),$ $\mathrm C(−1,−1),$ $\mathrm D(1,−1)$ を結ぶ最短経路の長さを考える.
「三角不等式」$\mathrm P\mathrm P'+\mathrm P'\mathrm P'' \geqq \mathrm P\mathrm P''$ を使った議論により, $y$ 軸に関して対称な $x$ 軸上の $2$ 点 $\mathrm P,$ $\mathrm Q$ (点 $\mathrm P$ の $x$ 座標は $0$ 以上 $1$ 以下) を分岐点とする経路の長さ
\[ L = \mathrm{PQ}+\mathrm{PA}+\mathrm{QB}+\mathrm{QC}+\mathrm{PD}\]
の最小値を求める問題に帰着できる (詳細は省略).
対称性により, $L$ の最小値は関数
\[ f(x) = \mathrm{PO}+\mathrm{PA}+\mathrm{PD} = \mathrm{PO}+2\mathrm{PA}\]
の最小値の $2$ 倍である.
\[\begin{aligned}
f(x) &= x+2\sqrt{(1-x)^2+(1-0)^2} = x+2\sqrt{x^2-2x+2}, \\
f'(x) &= 1+\frac{2x-2}{\sqrt{x^2-2x+2}} = \frac{2(x-1)+\sqrt{x^2-2x+2}}{\sqrt{x^2-2x+2}}
\end{aligned}\]
から,
\[\begin{aligned}
f'(x) = 0 &\iff 2(1-x) = \sqrt{x^2-2x+2} \\
&\ \ \Longrightarrow\; 4(1-x)^2 = x^2-2x+2 \\
&\iff 3x^2-6x+2 = 0 \\
&\ \ \Longrightarrow\; x = 1-\frac{1}{\sqrt 3}
\end{aligned}\]
が成り立つ.
よって, $f(x)$ の増減表は次の通りであるから, $f(x)$ は $x = 1-\dfrac{1}{\sqrt 3}$ のとき極小かつ最小の値 $1+\sqrt 3$ をとる.
最小値は, 点 $\mathrm P$ から辺 $\mathrm{AD}$ に下ろした垂線の足 $\mathrm H$ について,
$\mathrm{AH}:\mathrm{HP} = 1:\dfrac{1}{\sqrt 3} = \sqrt 3:1$ から $\mathrm{PA} = \dfrac{2}{\sqrt 3}$ であることを使って
\[\left( 1-\frac{1}{\sqrt 3}\right) +2\cdot\frac{2}{\sqrt 3} = 1+\frac{3}{\sqrt 3} = 1+\sqrt 3\]
と求めた.
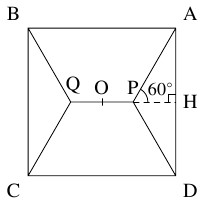 ゆえに, $L$ は $\mathrm P\left( 1-\dfrac{1}{\sqrt 3},0\right)$ のとき最小値 $2(1+\sqrt 3)$ をとるから, 最短経路の長さは正方形の周の長さの
ゆえに, $L$ は $\mathrm P\left( 1-\dfrac{1}{\sqrt 3},0\right)$ のとき最小値 $2(1+\sqrt 3)$ をとるから, 最短経路の長さは正方形の周の長さの
である.
| $x$ | $0$ | $\cdots$ | $1-\dfrac{1}{\sqrt 3}$ | $\cdots$ | $1$ |
| $f'(x)$ | $-$ | $0$ | $+$ | ||
| $f(x)$ | $\searrow$ | $1+\sqrt 3$ | $\nearrow$ |

| $\dfrac{2(1+\sqrt 3)}{8} = \dfrac{1+\sqrt 3}{4}$ (倍) |
さまざまな離散幾何学のクイズ
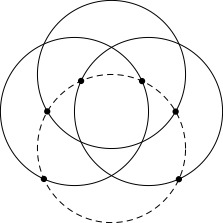
クイズ《円を用いたヴェン図の限界》
ある全体集合に属する集合を円で表し (集合の要素を円の内部または周上の点, 補集合の要素を円の外部の点に対応させる), 集合の共通部分を円の重なり (面積は正) で表す.
このとき, どのような集合も $1$ つの平面上に表せるのは, 集合が何個以下のときか.
(有名問題)
答え
$3$ 個以下.
解説
$n$ 個の円周により分割されてできる領域の個数の最大値を $a_n$ とおく.
一般に $n$ 個の集合それぞれに属するか否かは全部で $2^n$ 通りあるから, $n$ 個の集合が $1$ つの平面上に円を用いて表せるためには
\[ a_n \geqq 2^n\]
の成り立つことが必要である.
- (1)
- まず, 数列 $\{ a_n\}$ の一般項を求める.
$a_n$ は, どの $2$ 個も $2$ 点で交わり, どの $3$ 個も $1$ 点で交わらないように, 平面上に $n$ 個の円周をかくとき, 平面が分割されてできる領域の個数に等しい.
$n$ 個の円周をかいた状態から新たに $1$ 個の円周をかいていくと,
既存の各円周と $2$ 点で交わり, その各交点で領域が $1$ 個ずつ増えて, 全部で $2n$ 個の領域が増えるので,
\[ a_{n+1}-a_n = 2n\]
が成り立つ.
また, $a_1 = 2$ であるから, $n \geqq 2$ のとき \[\begin{aligned} a_n &= a_1+\sum_{k = 1}^{n-1}(a_{k+1}-a_k) \\ &= 2+\sum_{k = 1}^{n-1}2k \\ &= 2+2\cdot\frac{(n-1)n}{2} \\ &= n^2-n+2 \end{aligned}\] が成り立つ. これは $n = 1$ のときも成り立つ.
- (2)
- $n \leqq 4$ のとき $a_n$ の値を求めてみると
\[ a_1 = 2 = 2^1, \quad a_2 = 4 = 2^2, \quad a_3 = 8 = 2^3, \quad a_4 = 14 < 2^4\]
となるから, $n \geqq 4$ のとき $a_n < 2^n$ が成り立つことを示す.
\[ b_n = \frac{a_n}{2^n} = \frac{n^2-n+2}{2^n}\]
とおく.
$b_4 < 1$ であるから, $b_{n+1} < b_n$ であることを示せば,
\[\cdots < b_{n+1} < b_n < \cdots < b_4 < 1\]
となり, $b_n < 1$ つまり $a_n < 2^n$ であることが示せる.
そこで, $b_n,$ $b_{n+1}$ の比をとると,
\[\begin{aligned}
\frac{b_{n+1}}{b_n} &= \frac{(n+1)^2-(n+1)+2}{2^{n+1}}\div\frac{n^2-n+2}{2^n} \\
&= \frac{n^2+n+2}{2(n^2-n+2)}
\end{aligned}\]
となる.
$n \geqq 4$ のとき,
\[\begin{aligned}
2(n^2-n+2)-(n^2+n+2) &= n^2-3n+2 \\
&= (n-1)(n-2) > 0
\end{aligned}\]
であるから, $0 < n^2+n+2 < 2(n^2-n+2)$ であり,
が成り立つ. したがって, $n \geqq 4$ のとき $a_n < 2^n$ が成り立つ.$\dfrac{b_{n+1}}{b_n} < 1$ つまり $b_{n+1} < b_n$
参考
円を用いたヴェン図では一般に $3$ 個以下の集合の相関関係しか表せない.
クイズ《楕円の周による平面の分割》
$n$ 個の楕円の周により平面が分割されてできる領域の個数の最大値はいくらか.
(有名問題)
答え
$2(n^2-n+1).$
解説
$n$ 個の楕円の周により平面が分割されてできる領域の個数が最大になるのは, どの $2$ 個も $4$ 点で交わり, どの $3$ 個も $1$ 点で交わらないときである.
その最大値 $e_n$ は,
\[ e_1 = 2, \quad e_{n+1}-e_n = 4n\]
から
\[\begin{aligned}
e_n &= e_1+\sum_{k = 1}^{n-1}(e_{k+1}-e_k) = 2+\sum_{k = 1}^{n-1}4k \\
&= 2+4\cdot\frac{(n-1)n}{2} = 2(n^2-n+1)
\end{aligned}\]
である ($n = 1$ のときも成り立つ).
参考
先述の通り, 円を用いたヴェン図では一般に $3$ 個以下の集合の相関関係しか表せない.
しかし, $n$ 個の楕円の周により平面が分割されてできる領域の個数の最大値は $2(n^2-n+1)$ であり, その $n \leqq 5$ における値は
\[ 2,\ 6,\ 14,\ 26,\ 42\]
で $2^n$ 以上であるから, 楕円を用いたヴェン図で $5$ 個以下の集合の相関関係が表せる.
クイズ《平面における格子点を頂点とする正三角形》
方眼紙において, 横方向の罫線と縦方向の罫線の交点を格子点と呼ぶ.
$3$ 個の格子点を頂点とするような正三角形は存在するか.
存在するならばその一例を挙げ, 存在しないならばその理由を述べよ.
(有名問題, 参考: $1999$ 大阪大)
答え
存在しない (理由は解説を参照).
解説
各頂点の $x$ 座標, $y$ 座標が整数である正三角形 $\mathrm{OPQ}$ の存在を仮定する.
平行移動で面積は変わらないことから $\mathrm O$ が原点であるとしても一般性を失わないので, その場合を考える.
$\mathrm P(a,b),$ $\mathrm Q(c,d)$ とおく.
このとき, 辺 $\mathrm{OP}$ の長さは $\sqrt{a^2+b^2}$ であり, 直線 $\mathrm{OP}:bx-ay = 0$ と点 $\mathrm Q(c,d)$ の距離 $d$ は
\[ d = \frac{|bc-ad|}{\sqrt{b^2+(-a)^2}} = \frac{|ad-bc|}{\sqrt{a^2+b^2}}\]
であるから,
\[\begin{aligned}
\triangle\mathrm{OPQ} &= \frac{1}{2}\mathrm{OP}\cdot d \\
&= \frac{1}{2}\sqrt{a^2+b^2}\cdot\frac{|ad-bc|}{\sqrt{a^2+b^2}} \\
&= \frac{1}{2}|ad-bc| \quad \cdots [1]
\end{aligned}\]
が成り立つ.
また, $\triangle\mathrm{OPQ}$ が正三角形であることから,
\[\triangle\mathrm{OPQ} = \frac{1}{2}\mathrm{OP}^2\sin 60^\circ = \frac{\sqrt 3}{4}(a^2+b^2) \quad \cdots [2]\]
が得られる.
よって, $[1],$ $[2]$ から,
\[\sqrt 3 = \frac{2|ad-bc|}{a^2+b^2}\]
が成り立つ.
$a,$ $b,$ $c,$ $d$ は整数であることから右辺は有理数であるが, これは $\sqrt 3$ が無理数であることに反する.
ゆえに, 各頂点の $x$ 座標, $y$ 座標が整数であるような正三角形は存在しない.
ゆえに, 各頂点の $x$ 座標, $y$ 座標が整数であるような正三角形は存在しない.
クイズ《空間における格子点を頂点とする正六角形》
平面や空間において, 座標の各成分が整数である点を格子点と呼ぶ.
平面において $6$ 個の格子点を頂点とするような正六角形は存在しないことが知られている.
それでは, 空間において $6$ 個の格子点を頂点とするような正六角形は存在するか.
存在するならばそのような正六角形の $1$ 辺の長さの最小値を求め, 存在しないならばその理由を述べよ.
(有名問題, 参考: $2024$ 早稲田大)
答え
$\sqrt 2.$
解説
$8$ 個の格子点 $(\pm 1,\pm 1,\pm 1)$ (複号任意) を頂点とする立方体 ($1$ 辺の長さは $2$) を $3$ 本の辺の中点 $(1,1,0),$ $(0,1,1),$ $(-1,0,1)$ を通る平面で切断すると, 切り口にはこれら $3$ 個の格子点を頂点とする正六角形ができて, その残りの頂点も $(-1,-1,0),$ $(0,-1,-1),$ $(1,0,-1)$ と格子点になり, $1$ 辺の長さは $\sqrt 2$ になる.
また, $2$ つの格子点の距離のうち最小のものは $\sqrt{0^2+0^2+1^2} = 1,$ その次に小さいものは $\sqrt{0^2+1^2+1^2} = \sqrt 2$ であり, $1$ 辺の長さが $1$ の正六角形は存在しない (与えられた格子点から距離が $1$ の格子点は $x$ 軸, $y$ 軸, $z$ 軸のいずれかの方向に $\pm 1$ だけ平行移動した位置にしかないことからわかる) から, 求める正六角形の $1$ 辺の長さの最小値は $\sqrt 2$ である.
また, $2$ つの格子点の距離のうち最小のものは $\sqrt{0^2+0^2+1^2} = 1,$ その次に小さいものは $\sqrt{0^2+1^2+1^2} = \sqrt 2$ であり, $1$ 辺の長さが $1$ の正六角形は存在しない (与えられた格子点から距離が $1$ の格子点は $x$ 軸, $y$ 軸, $z$ 軸のいずれかの方向に $\pm 1$ だけ平行移動した位置にしかないことからわかる) から, 求める正六角形の $1$ 辺の長さの最小値は $\sqrt 2$ である.
クイズ《シュタインハウスの問題》
方眼紙において, 横方向の罫線と縦方向の罫線の交点を格子点と呼ぶ.
与えられた正の整数 $n$ に対して, ちょうど $n$ 個の格子点を含むような円は存在するか.
ヒント: 点 $\left(\sqrt 2,\dfrac{1}{3}\right)$ からそれぞれの格子点までの距離を考えてみよ.
(有名問題)
答え
存在する.
解説
$xy$ 平面において $x$ 座標, $y$ 座標が整数である点を格子点と呼ぶ.
$\mathrm C\left(\sqrt 2,\dfrac{1}{3}\right)$ とおく.
$\mathrm P(x,y),$ $\mathrm P'(x',y')$ を格子点とし, $\mathrm{CP} = \mathrm{CP}'$ として, $\mathrm P = \mathrm P'$ を示す.
このとき, $\mathrm{CP}^2 = \mathrm{CP}'{}^2$ から,
\[ (x-\sqrt 2)^2+\left( y-\frac{1}{3}\right) ^2 = (x'-\sqrt 2)^2+\left( y'-\frac{1}{3}\right) ^2\]
が成り立つ.
両辺を展開して整理すると,
\[ 2(x-x')\sqrt 2 = x^2-x'{}^2+y^2-y'{}^2-\frac{2}{3}(y-y')\]
となる.
$\sqrt 2$ が無理数で $x,$ $x'$ が整数であるから, 左辺は $0$ か無理数である.
一方, $x,$ $y,$ $x',$ $y'$ は整数であるから, 右辺は有理数である.
よって, $x-x' = 0$ つまり $x = x'$ である.
このとき,
\[ 0 = y^2-y'{}^2-\frac{2}{3}(y-y') = \left( y+y'-\frac{2}{3}\right) (y-y')\]
となる.
$y+y'$ が整数であることから $y+y'-\dfrac{2}{3} \neq 0$ であり, $y-y' = 0$ から $y = y'$ が得られる.
よって, $\mathrm P = \mathrm P'$ である.
ゆえに, 点 $\mathrm C$ からそれぞれの格子点までの距離はすべて異なるから, ちょうど $n$ 個の格子点を含むような円は存在する.
ゆえに, 点 $\mathrm C$ からそれぞれの格子点までの距離はすべて異なるから, ちょうど $n$ 個の格子点を含むような円は存在する.
参考
- すべての正の整数 $n$ に対して, ちょうど $n$ 個の「格子点」を含むような円は存在するかという「シュタインハウスの問題」は, $1957$ 年にシュタインハウス (H. Steinhaus) によって提起され, 上記の命題を示すことでシェルピンスキー (W. Sierpinski) によって肯定的に解決された. つまり, 点 $\mathrm C$ を中心とする円の半径を大きくしていくと, 円に含まれる「格子点」は $1$ 個ずつ増えていく. また, ちょうど $n$ 個の「格子点」($xyz$ 空間において $x$ 座標, $y$ 座標, $z$ 座標が整数である点) を含むような球が存在することも知られている.
- これとは別に, ちょうど $n$ 個の「格子点」を通る円周は存在するかという問題も, $1958$ 年にシンゼル (A. Schinzel) によって肯定的に解決されている. また, ちょうど $n$ 個の「格子点」を通る球面が存在することも知られている (クリコフスキーの定理).
クイズ《頂点と内心が格子点である鋭角三角形》
$xy$ 平面において $x$ 座標も $y$ 座標も整数である点を格子点と呼ぶ.
格子点を頂点とする鋭角三角形のうち, 内心も格子点である三角形の例を挙げよ.
(オリジナル)
答え
$3$ 点 $\mathrm A(0,0),$ $\mathrm B(14,0),$ $\mathrm C(5,12)$ を結ぶ $\triangle\mathrm{ABC}.$
解説
$xy$ 平面において $x$ 座標も $y$ 座標も有理数である点を有理点と呼ぶ.
有理点を頂点とする鋭角三角形のうち内心も有理点である三角形が構成できれば, 適当な倍率に拡大することで所望の三角形が得られる.
格子点 (より一般には有理点) を通り, 傾きが有理数であるような $2$ 直線の交点は有理点であることを利用して, このような三角形を構成する.
- (1)
- 簡単のため (角の二等分線の方向ベクトルの公式, または三角形の内心の位置ベクトルの公式を考慮して), 格子点を頂点とし, $3$ 辺の長さが整数である鋭角三角形を構成する. このような直角三角形としては, $3$ 辺の長さが $3,$ $4,$ $5$ である直角三角形, $5,$ $12,$ $13$ である直角三角形 ($2$ 辺が座標軸と平行になるように配置する) が考えられる. 前者の直角三角形を $3$ 倍に拡大して長さが $12$ の辺を貼り合わせると, $3$ 点 $\mathrm A(0,0),$ $\mathrm B(14,0),$ $\mathrm C(5,12)$ を結ぶ鋭角三角形 $\mathrm{ABC}$ が得られ, $\mathrm{BC} = 15,$ $\mathrm{CA} = 13,$ $\mathrm{AB} = 14$ となる.
- (2)
- $\triangle\mathrm{ABC}$ の内心 $\mathrm I$ の座標を求める.
$\angle\mathrm A,$ $\angle\mathrm B$ の二等分線の方向ベクトルとしてそれぞれ
\[\begin{aligned}
\frac{\overrightarrow{\mathrm{AB}}}{|\overrightarrow{\mathrm{AB}}|}+\frac{\overrightarrow{\mathrm{AC}}}{|\overrightarrow{\mathrm{AC}}|} &= (1,0)+\frac{(5,12)}{13} = \frac{1}{13}(18,12), \\
\frac{\overrightarrow{\mathrm{BA}}}{|\overrightarrow{\mathrm{BA}}|}+\frac{\overrightarrow{\mathrm{BC}}}{|\overrightarrow{\mathrm{BC}}|} &= (-1,0)+\frac{(-9,12)}{15} = \frac{1}{5}(-8,4)
\end{aligned}\]
がとれるから, $\angle\mathrm A,$ $\angle\mathrm B$ の二等分線の方程式はそれぞれ
\[ y = \frac{2}{3}x, \quad y = -\frac{1}{2}(x-14)\]
である.
$\mathrm I$ はこれら $2$ 本の二等分線の交点であるから,
\[\mathrm I(6,4)\]
である.
これは格子点であるから, 拡大するまでもなく, $\triangle\mathrm{ABC}$ が求める三角形の例を与える.
なお, 内心 $\mathrm I$ の座標は, $3$ 辺の長さが $\mathrm{BC} = a,$ $\mathrm{CA} = b,$ $\mathrm{AB} = c$ である $\triangle\mathrm{ABC}$ の内心の位置ベクトルの公式 \[\overrightarrow{\mathrm{OI}} = \frac{a\overrightarrow{\mathrm{OA}}+b\overrightarrow{\mathrm{OB}}+c\overrightarrow{\mathrm{OC}}}{a+b+c}\] (こちらを参照) により, \[\overrightarrow{\mathrm{OI}} = \frac{15(0,0)+13(14,0)+14(5,12)}{15+13+14} = (6,4)\] であることから求めることもできる.
参考
頂点と内心が有理点であるような三角形の構成法 (任意の三角形が構成可能) については, 「日曜数学 Advent Calendar $2025$」の $18$ 日目の記事「頂点と五心がすべて有理点である三角形」を参照されたい.