有名問題・定理から学ぶ数学
Well-Known Problems and Theorems in Mathematics
数式を枠からはみ出さずに表示するためには, 画面を横に傾けてください.
格子点を通る直線・角の二等分線とペル方程式
§1 はじめに
- この記事は「日曜数学 Advent Calendar $2023$」の $20$ 日目の記事として書かれたものです.
- $19$ 日目の記事は, ともさんの『三角形の垂心が満たす性質についての考察』でした.
- $21$ 日目の記事は, 圏論のあか☆ねこさんの『オイラーの定理の評価はガバだというお話』です.
※ 一部の記号は, 代数的整数論の専門書寄りにしたため, 昨年の記事と異なるものもございますが, ご了承ください.
こんにちは. 廣津孝です. 皆さんとともに数学を通してクリスマスのお祝いができることを大変うれしく思います.
昨年 ($2022$ 年) の記事では, 平面上の $2$ 直線の傾き $a,$ $b$ とそれらのなす角の二等分線の傾き $c$ がすべて整数になるような $a,$ $b,$ $c$ の値に関する定理についてご紹介しました.
筆者は最近, それを一般化して, 平面上で $2$ 直線とそれらのなす角の二等分線が格子点を結んで描ける条件を決定しました. 内容は相変わらず中学生にも理解できる素朴なもので, 解の一部にはおなじみのピタゴラスの $3$ つ組 (ピタゴラス数) も登場します. 証明には $2$ 次体の整数論 (ヒルベルトの分岐理論, イデアル類群の有限性など) を使いますが, 解の構造については高校生でも理解できる部分も多いので, その部分を中心に概要を解説したいと思います.
方眼ノートや描画ソフトを使うとき, 格子点 ($xy$ 平面上の $x$ 座標も $y$ 座標も整数である点) を結んで直線を引くと, 正確な描画ができます. このとき自然に現れるのが, 与えられた格子点 $\mathrm O,$ $\mathrm A,$ $\mathrm B$ に対して, $\angle\mathrm{AOB}$ の二等分線が頂点 $\mathrm O$ と他の格子点 $\mathrm C$ を結ぶことで描けるのはいつかという問題です. これは, 次の問題と等価です.
問題 1
どのような有理数 $a,$ $b$ $(|a| \neq |b|)$ に対して, 傾きが $a,$ $b$ である $2$ 直線のなす角 (鋭角または鈍角) の二等分線の傾き $c$ は有理数になるか.
これは,
命題 1
$a,$ $b,$ $c$ $(|a| \neq \pm |b|)$ を実数とする.
傾きが $a,$ $b$ の $2$ 直線のなす角の二等分線の傾きが $c,$ $-c^{-1}$ であるとき, $a,$ $b,$ $c$ は
を満たす.
により,
問題 1'
方程式
\[ (a-c)^2(b^2+1) = (b-c)^2(a^2+1) \quad \cdots [\star ]\]
の非自明な有理数解をすべて求めよ.
という問題に言い換えられるのでした.
方程式 $[\star ]$ は, 今回の記事の主役なので, よく覚えておいてください.
ここで, $2$ 直線のなす角 $\theta$ は $0^\circ \leqq \theta \leqq 180^\circ$ の範囲で考えているのですが, $|a| = |b|$ の場合, 角の二等分線の傾き $c$ が有理数になるのは $(a,b,c) = (a,a,c),$ $(a,-a,0)$ のときに限るので, 非自明解と呼んで除外して考えています.
昨年ご紹介したように,
定理 1 (廣津 [2, Theorem 1])
ネガティブなペル方程式 $x^2-dy^2 = -1$ が解をもつような, 平方因数をもたない正の整数 $d\,(> 1)$ に対して, $|x^2-dy^2| = 1$ の $n$ 番目に小さい正の整数解を $(x,y) = (f_n^{(d)},g_n^{(d)})$ とおく.
このとき, $[\star ]$ の非自明な整数解は, $a,$ $b$ の入れ替えを許せば, 適当な正の整数 $d,$ $m,$ $n$ について
または
の形に表される.
| $(a,b,c) = \pm\left( f_{(2m-1)(2n-1)}^{(d)},f_{(2m-1)(2n+1)}^{(d)},\dfrac{g_{(2m-1)\cdot 2n}^{(d)}}{g_{2m-1}^{(d)}}\right)$ |
で $[\star ]$ の整数解はすべて求まっているのですが (証明はこちら), 次の例のように絶対値が大きな整数解が多い (問題 1 の言葉で言うと傾きが急な直線が多い) ので, 絶対値が小さい有理数解も求めたい (小さい方眼ノートの格子点を結んで $2$ 直線と角の二等分線が描ける例をもっと見つけたい) というのが今回の研究の動機です.
例 1
- (1)
- $|x^2-2y^2| = 1$ からは, \[\begin{aligned} &(f_1^{(2)},f_3^{(2)}) & &\!\!\!\!\!\!\!\!\!\!\!\!(f_3^{(2)},f_5^{(2)}) & &\!\!\!\!(f_5^{(2)},f_7^{(2)}) \\ &= (1,7), & &\!\!\!\!\!\!\!\!\!\!\!\!= (7,41), & &\!\!\!\!= (41,239),\ \cdots \\ &(f_3^{(2)},f_9^{(2)}) & &\!\!\!\!\!\!\!\!\!\!\!\!(f_9^{(2)},f_{15}^{(2)}) & &\!\!\!\!(f_{15}^{(2)},f_{21}^{(2)}) \\ &= (7,1393), & &\!\!\!\!\!\!\!\!\!\!\!\!= (1393,275807), & &\!\!\!\!= (275807,54608393),\ \cdots \\ &(f_5^{(2)},f_{15}^{(2)}) & & & & \\ &= (41,275807), & &\!\!\!\!\cdots & & \\ &\qquad\vdots \end{aligned}\] または \[\begin{aligned} &(f_1^{(2)},-f_3^{(2)}) & &(f_3^{(2)},-f_5^{(2)}) & &(f_5^{(2)},-f_7^{(2)}) \\ &= (1,-7), & &= (7,-41), & &= (41,-239), \quad \cdots \\ \end{aligned}\] を $(a,b)$ の値とする問題 1 の解が得られます.
- (2)
- $|x^2-5y^2| = 1$ からは, \[\begin{aligned} &(f_1^{(5)},f_3^{(5)}) & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!(f_3^{(5)},f_5^{(5)}) & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!(f_5^{(5)},f_7^{(5)}) \\ &= (2,38), & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= (38,682), & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= (682,12238),\ \cdots \\ &(f_3^{(5)},f_9^{(5)}) & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!(f_9^{(5)},f_{15}^{(5)}) & & \\ &= (38,219602), & &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= (219602,1268860318), & &\cdots \\ &(f_5^{(5)},f_{15}^{(5)}) & & & & \\ &= (682,1268860318), & &\!\!\!\!\cdots & & \\ &\qquad\vdots \end{aligned}\] を $(a,b)$ の値とする問題 1 の解が得られます.
§2 解の分類
$[\ast ]$ を解くうえで鍵になるのが, 次の命題です.
命題 2
$[\ast ]$ の非自明な有理数解 $(a,b,c)$ は, 平方因数をもたないある正の整数 $d$ について,
\[ x^2-dy^2 = -1\]
の有理数解 $(x,y) = (a_1,a_2),$ $(b_1,b_2)$ を用いて
の形に表される.
| $(a,b,c) = \left( a_1,b_1,\dfrac{a_1b_2+a_2b_1}{b_2+a_2}\right),\ \left( a_1,b_1,\dfrac{a_1b_2-a_2b_1}{b_2-a_2}\right)$ |
証明
$(a,b,c) = (a_1,b_1,c_1)$ を $[\ast ]$ の非自明な有理数解とし,
($A_1,$ $B_1,$ $C_1,$ $Z$: 整数, $Z \neq 0$) とします.
これらを $[\ast ]$ に代入して $Z^4$ を掛けると,
\[ (A_1-C_1)^2(B_1{}^2+Z^2) = (B_1-C_1)^2(A_1{}^2+Z^2) \quad \cdots [1]\]
が得られます.
両辺の素因数分解に着目すると, $(A_1-C_1)^2,$ $(B_1-C_1)^2$ が平方数であることから, $A_1{}^2+Z^2,$ $B_1{}^2+Z^2$ において指数が奇数であるような素因数の組合せは等しいと分かります.
そのような素因数の積を $d$ とおくと (存在しなければ $d = 1$ と定めます),
\[ A_1{}^2+Z^2 = dA_2{}^2, \quad B_1{}^2+Z^2 = dB_2{}^2 \quad \cdots [2]\]
($A_2,$ $B_2$: 整数) と表されるので, $A_1,$ $B_1$ は
\[ X^2-dY^2 = -Z^2\]
の整数解 $(X,Y) = (A_1,A_2),$ $(B_1,B_2)$ の $X$ 成分になり, $a_2 = \dfrac{A_2}{Z},$ $b_2 = \dfrac{B_2}{Z}$ とおくと $a_1,$ $b_1$ は
\[ x^2-dy^2 = -1\]
の有理数解 $(x,y) = (a_1,a_2),$ $(b_1,b_2)$ の $x$ 成分になります.
$[1]$ に $[2]$ を代入して $d$ で割ると
\[ (A_1-C_1)^2B_2{}^2 = (B_1-C_1)^2A_2{}^2\]
つまり
\[ (A_1-C_1)B_2 = \pm (B_1-C_1)A_2.\]
となります.
\[ B_2{}^2-A_2{}^2 = \frac{B_1{}^2-A_1{}^2}{d} = \frac{(b_1{}^2-a_1{}^2)Z^2}{d} \neq 0\]
であることに注意し, これを $C_1$ について解くと
\[ C_1 = \frac{A_1B_2+A_2B_1}{B_2+A_2}, \frac{A_1B_2-A_2B_1}{B_2-A_2}\]
つまり
\[ c_1 = \frac{a_1b_2+a_2b_1}{b_2+a_2}, \frac{a_1b_2-a_2b_1}{b_2-a_2}\]
が得られます.
| $a_1 = \dfrac{A_1}{Z},$ $b_1 = \dfrac{B_1}{Z},$ $c_1 = \dfrac{C_1}{Z}$ |
$d = 1$ の場合と $d > 1$ の場合で, 解の構造は大きく異なります. 後者の場合に $\mathbb Q(\sqrt d)$ を有理数体 $\mathbb Q$ (有理数全体が通常の加減乗除に関してなす数の体系) に $\sqrt d$ を添加して得られる $2$ 次体, つまり $\alpha = a_1+a_2\sqrt d$ $(a_1,$ $a_2 \in \mathbb Q)$ の形の実数全体とし, $\alpha$ の共役 $\alpha ',$ ノルム $N(\alpha )$ をそれぞれ
定理 2 (廣津 [1, Theorem 2 の前半])
$(a,b,c)$ を $[\ast ]$ の非自明な有理数解とする.
- (I)
- $a,$ $b$ が $x^2-y^2 = -1$ の有理数解の $x$ 成分である場合.
$(a,b,c)$ は, $|l| \neq |m|,$ $lm \neq n^2,$ $lmn \neq 0$ を満たす整数 $l,$ $m,$ $n$ を用いて
(複号同順) の形に表される.$(a,b,c) = \left(\dfrac{l^2-n^2}{2ln},\dfrac{m^2-n^2}{2mn},\pm\left(\dfrac{lm-n^2}{(l+m)n}\right) ^{\pm 1}\right)$ - (II)
- $a,$ $b$ が $x^2-dy^2 = -1$ ($d$: 平方因数をもたない $1$ より大きい整数) の有理数解の $x$ 成分である場合.
$(a,b,c)$ は, $N(\alpha ) = N(\beta ) = -1,$ $\beta \neq \pm\alpha$ を満たす $\alpha,$ $\beta \in \mathbb Q(\sqrt d)$ を用いて
(複号同順) の形に表される.$(a,b,c) = \left(\dfrac{\alpha +\alpha '}{2},\dfrac{\beta +\beta '}{2},\pm\left(\dfrac{\alpha\beta\!-\!(\alpha\beta )'}{\alpha\!+\beta\!-\!(\alpha\!+\!\beta )'}\right) ^{\pm 1}\right)$
証明
- (I)
- $a,$ $b$ がそれぞれ $x^2-y^2 = -1$ の有理数解 $(x,y) = (a_1,a_2),$ $(b_1,b_2)$ の $x$ 成分である場合. \[ a_1 = \frac{A_1}{n}, \quad a_2 = \frac{A_2}{n}, \quad b_1 = \frac{B_1}{n}, \quad b_2 = \frac{B_2}{n}\] ($A_1,$ $A_2,$ $B_1,$ $B_2,$ $n$: 整数, $n \neq 0$) とおきます. このとき, \[ A_2{}^2-A_1{}^2 = B_2{}^2-B_1{}^2 = n^2\] が成り立つので, \[ A_2+A_1 = l, \quad B_2+B_1 = m\] とおくと, \[ A_2-A_1 = \frac{n^2}{l}, \quad B_2-B_1 = \frac{n^2}{m}\] から \[\begin{aligned} a_1 &= \frac{l-n^2/l}{2n} = \frac{l^2-n^2}{2ln}, & a_2 &= \frac{l+n^2/l}{2n} = \frac{l^2+n^2}{2ln}, \\ b_1 &= \frac{m-n^2/m}{2n} = \frac{m^2-n^2}{2mn}, & b_2 &= \frac{m+n^2/m}{2n} = \frac{m^2+n^2}{2mn}, \end{aligned}\] となり, \[\begin{aligned} \frac{a_1b_2+a_2b_1}{b_2+a_2} &= \frac{1}{2}\cdot\frac{(l^2-n^2)(m^2+n^2)+(l^2+n^2)(m^2-n^2)}{ln(m^2+n^2)+mn(l^2+n^2)} \\ &= \frac{1}{2}\cdot\frac{2(l^2m^2-n^4)}{n(lm+n^2)(l+m)} = \frac{lm-n^2}{(l+m)n}, \\ \frac{a_1b_2-a_2b_1}{b_2-a_2} &= -\left(\frac{a_1b_2+a_2b_1}{b_2+a_2}\right) ^{-1} = -\frac{(l+m)n}{lm-n^2} \end{aligned}\] となるので, 上記の公式が得られます. ここで, $2$ 本の角の二等分線は互いに垂直であり, それらの傾きの積は $-1$ であることを使いました.
- (II)
- $a,$ $b$ がそれぞれ $x^2-dy^2 = -1$ ($d$: 平方因数をもたない $1$ より大きい整数) の有理数解 $(x,y) = (a_1,a_2),$ $(b_1,b_2)$ の $x$ 成分である場合. 一般に, $\alpha = a_1+a_2\sqrt d,$ $\beta = b_1+b_2\sqrt d$ ($a_1,$ $a_2,$ $b_1,$ $b_2$: 整数) のとき, \[\begin{aligned} &a_1 = \frac{\alpha +\alpha '}{2}, \quad b_1 = \frac{\beta +\beta '}{2}, \\ &a_1b_2+a_2b_1 = \frac{\alpha\beta -(\alpha\beta )'}{2\sqrt d}, \\ &a_2+b_2 = \frac{(\alpha +\beta )-(\alpha +\beta )'}{2\sqrt d}. \end{aligned}\] が成り立つので, 上記の公式が得られます.
よく見ると, 公式にはピタゴラスの $3$ つ組 (こちらを参照) が現れています (ピタゴラスの $3$ つ組は整数 $m,$ $n$ $(m > n)$ を用いて \[ (m^2-n^2,2mn,m^2+n^2)\] の形に表されることを思い出しましょう). つまり, (I) の場合の $[\ast ]$ の有理数解 $(a,b,c)$ において, $a,$ $b$ の値はそれぞれピタゴラスの三角形の直角を挟む $2$ 辺の長さの比として表せます.
例 2
- (I)
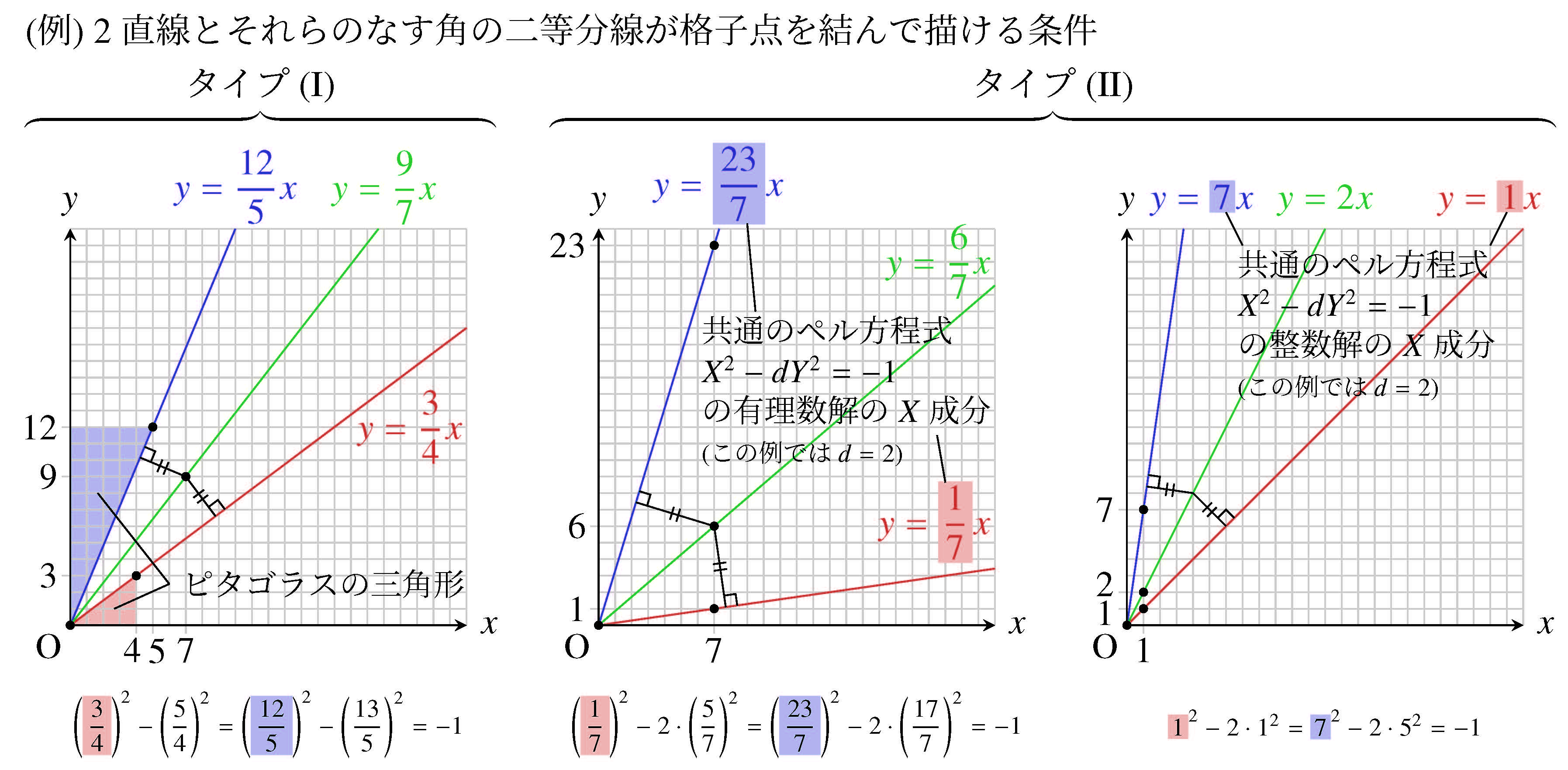
- $x^2-y^2 = -1$ の有理数解 \[ (x,y) = \left(\dfrac{3}{4},\dfrac{5}{4}\right),\ \left(\dfrac{12}{5},\dfrac{13}{5}\right)\] からは, $[\ast ]$ の有理数解 \[ (a,b,c) = \left(\frac{3}{4},\frac{12}{5},\frac{9}{7}\right)\] が得られます.
- (II)
- $x^2-2y^2 = -1$ の有理数解 \[ (x,y) = \left(\dfrac{1}{7},\dfrac{5}{7}\right),\ \left(\dfrac{23}{7},\dfrac{17}{7}\right)\] および整数解 \[ (x,y) = (1,1),\ (7,5)\] からは, $[\ast ]$ の有理数解 \[ (a,b,c) = \left(\frac{1}{7},\frac{23}{7},\frac{6}{7}\right)\] および整数解 \[ (a,b,c) = (1,2,7)\] が得られます.
これらの例を図にまとめると, 次のようになります (大きめに作ったので, 右クリックで開いて拡大して見るのもおすすめです).
§3 ペル方程式の有理数解
定理 2 において $[\ast ]$ の有理数解は, (I) の場合にはパラメーター $l,$ $m,$ $n$ を用いて明示的に表されていますが, (II) の場合にはまだはっきり表されているとは言えません. そこで, この節では $d$ を平方因数をもたない $1$ より大きい整数として, $x^2-dy^2 = -1$ の有理数解がどのように表されるのかについて解説します.
$|x^2-dy^2| = 1$ を斉次化する ($x = \dfrac{X}{Z},$ $y = \dfrac{Y}{Z}$ を代入して分母を払う) と $|X^2-dY^2| = Z^2$ となるので, まず右辺を $Z$ に置き換えた方程式 $|X^2-dY^2| = Z$ の整数解について考えることにします.
数値実験として, WolframAlphaで, 与えられた $d,$ $Z$ の値に対する整数解の挙動を調べてみると, \[ |X^2-dY^2| = Z\] が $X,$ $Y$ が互いに素であるような整数解をもつには, $Z$ の各素因数 $p \neq 2$ に対し, $\mathrm{ord}_p(Z)$($Z$ の素因数分解における $p$ の指数) のある約数 $l > 0$ に対して \[ |X^2-dY^2| = p^l\] が $X,$ $Y$ が互いに素であるような整数解をもつことが必要であるという予想が立ちます. 例えば, $X^2-2Y^2 = -7^2\cdot 17^2$ は解 $(X,Y) = (79,101)$ をもち, $X^2-2Y^2 = 7$ は解 $(X,Y) = (3,1)$ を, $X^2-2Y^2 = 17$ は解 $(X,Y) = (5,2)$ をもちます.
一般に, $0$ でない整数 $Z,$ $W$ に対して, $X^2-dY^2 = Z,$ $X^2-dY^2 = W$ がそれぞれ整数解 $(X,Y) = (a_1,a_2),$ $(b_1,b_2)$ をもつとき, ノルムの乗法性
| $N(\alpha\beta ) = N(\alpha )N(\beta )$ $(\alpha,\ \beta \in \mathbb Q(\sqrt d))$ |
定義 1
$Z$ を正の整数とする.
- (1)
- $|X^2-dY^2| = Z$ の整数解 $(X,Y)$ は, $X,$ $dY$ が互いに素であるとき, 狭義原始的であるという.
- (2)
- $X^2-dY^2 = Z,$ $X^2-dY^2 = -Z,$ $|X^2-dY^2| = Z$ の各方程式について, 狭義原始的な正の整数解のうち $Y$ の値が最小であり, さらにそのうち $X$ の値が最小であるものを基本解と呼ぶ.
- (3)
- ある正の整数 $l$ に対して $|X^2-dY^2| = p^l$ が狭義原始的な整数解をもつような素数 $p$ 全体の集合を $S(d)$ で表す.
- 各 $p \in S(d)$ に対して, $|X^2-dY^2| = p^l$ が狭義原始的な整数解をもつような正の整数 $l$ の最小値を $l_p$ で表し,
\[\begin{cases}
X^2-dY^2 = p^{l_p} & (x^2-dy^2 = -1\text{ が整数解をもつとき}), \\
|X^2-dY^2| = p^{l_p} & (\text{その他のとき}).
\end{cases}\]
の基本解 $(X,Y) = (X_p,Y_p)$ について
と定める.$\xi _p = X_p+Y_p\sqrt d$
- $X_p{}^2-dY_p{}^2 = -p^{l_p}$ を満たす $p \in S(d)$ 全体の集合を $S(d)_-$ で表す.
- ある正の整数 $l$ に対して $|X^2-dY^2| = p^l$ が狭義原始的な整数解をもつような素数 $p$ 全体の集合を $S(d)$ で表す.
例 3
- (1)
- (i)
- $X^2-2Y^2 = -7^2\cdot 17^2$ は狭義原始的な整数解 $(X,Y) = (79,101)$ をもちます.
- (ii)
- $|X^2-34Y^2| = 3$ は狭義原始的な整数解をもちません.
- (2)
- (i)
- $X^2-2Y^2 = 7$ の基本解は $(X,Y) = (3,1),$ $X^2-2Y^2 = 17$ の基本解は $(X,Y) = (5,2)$ です.
- (ii)
- $X^2-34Y^2 = -3^2$ の基本解は $(X,Y) = (5,1),$ $X^2-34Y^2 = 47$ の基本解は $(X,Y) = (9,1)$ です.
- (3)
- (i)
- $d = 2$ のとき. $7,$ $17 \in S(d),$ $l_7 = l_{17} = 1,$ $\xi _7 = 3+\sqrt 2,$ $\xi _{17} = 5+2\sqrt 2,$ $S(d)_- = \varnothing$ です.
- (ii)
- $d = 34$ のとき. $3,$ $47 \in S(d),$ $l_3 = 2,$ $l_{47} = 1,$ $\xi _3 = 5+\sqrt{34},$ $\xi _{47} = 9+\sqrt{34},$ $3 \in S(d)_-$ です.
ちなみに, $d = 2$ のとき $l_p$ の値はすべて $1$ なのですが, $d = 34$ のとき $l_3 = 2$ のように $l_p > 1$ となることがあります. これは, 定理 4 (3) で後述するように, $\mathbb Q(\sqrt d)$ の類数が $d = 2$ のとき $1,$ $d = 34$ のとき $2$ であることに由来しています.
$\mathbb Q(\sqrt d)$ の基本単数 ($|x^2-dy^2| = 4$ の正の整数解 $(x,y)$について $\dfrac{x+y\sqrt d}{2}$ の最小値) と $\xi _p$ $(p \in S(d))$ を用いると, ペル方程式の有理数解は, 次のように表すことができます.
定理 3 (廣津 [1, Theorem 8])
$\eta$ を $\mathbb Q(\sqrt d)$ の基本単数とし, $r \in \{ 0,1\}$ とする.
$x^2-dy^2 = (-1)^r$ の有理数解 $(x,y)$ は,
\[ l_pn_p \equiv 0 \pmod 2\]
および
\[ r \equiv \begin{cases}
n\qquad\quad\pmod 2 & (x^2-dy^2 = -1\text{ が整数解をもつとき}), \\
\displaystyle\sum_ {p \in S(d)_-}n_p\ (\mathrm{mod}\ 2) & (\text{その他のとき}).
\end{cases}\]
を満たす整数 $n,$ $n_p$ と $\mathbb Q(\sqrt d)$ の元 $\xi _p^* \in \{\xi _p,\xi _p'\}$ $(p \in S(d))$ について
を満たす (積は実質的有限積).
| $x+y\sqrt d = \pm\eta ^n\displaystyle\prod_{p \in S(d)}\xi _p^*{}^{n_p}p^{-l_pn_p/2}$ |
この公式から直ちに, 定理 2 における $\alpha,$ $\beta$ は, 次のように表されると分かります.
定理 2' (廣津 [1, Theorem 2 の後半])
定理 2 において, $\alpha,$ $\beta \in \mathbb Q(\sqrt d)$ は
\[ l_pm_p \equiv l_pn_p \equiv 0 \pmod 2\]
および
\[ 1 \equiv \left\{\begin{array}{l}
m \equiv n \pmod 2 \quad (x^2-dy^2 = -1 \text{ が整数解をもつとき}), \\
\displaystyle\sum_ {p \in S(d)_-}m_p \equiv \sum_ {p \in S(d)_-}n_p \pmod 2 \qquad\quad\ \ (\text{その他のとき}).
\end{array}\right.\]
を満たす整数 $m,$ $n,$ $m_p,$ $n_p$ と $\mathbb Q(\sqrt d)$ の元 $\alpha _p,$ $\beta _p \in \{\xi _p,\xi _p'\}$ $(p \in S(d))$ を用いて
の形に表される (積は実質的有限積).
定理 3 の証明には, $|X^2-dY^2| = Z$ の狭義原始的な整数解の存在条件に関する, 次の定理を使います. 代数的整数論におけるヒルベルトの分岐理論, イデアル類群の有限性を使うので多少専門的ですが, 初学者でもご興味のある方は青木氏の『素数と $2$ 次体の整数論』などを片手に読んでみてください. 複雑な場合分けが生じているのは, $\mathbb Q(\sqrt d)$ の整数環が
| $d \equiv 1\ (\text{mod}\ 4)$ のとき | $\mathbb Z\left[\dfrac{1+\sqrt d}{2}\right],$ |
| $d \equiv 2,$ $3\ (\text{mod}\ 4)$ のとき | $\mathbb Z[\sqrt d]$ |
定理 4 (廣津 [1, Theorem 6])
- (1)
- $p$ を素数とし, $d \not\equiv 5\ (\mathrm{mod}\ 8)$ または $p \neq 2$ とする. このとき, $p$ のある倍数 $Z > 0$ に対して $|X^2-dY^2| = Z$ が狭義原始的な整数解をもつのは, $p$ が $\mathbb Q(\sqrt d)$ で分解する場合に限る.
- (2)
- $d \equiv 1\ (\mathrm{mod}\ 4)$ とする.
- (a)
- $2 \in S(d)$ ならば, $l_2 \geqq 2$ である.
- (b)
- $2 \in S(d)$ と $l_2 = 2$ が成り立つのは $\eta \notin \mathbb Z[\sqrt d]$ である場合に限る. このとき, $\xi _2 = 2\eta$ である.
- (c)
- $d \equiv 5\ (\mathrm{mod}\ 8)$ かつ $Z$ が $8$ の倍数であるとき, $X^2-dY^2 = Z$ の整数解は偶数のペアである (狭義原始的でない).
- (3)
- (a)
- $d \equiv 1\ (\mathrm{mod}\ 8)$ または “$d \equiv 5\ (\mathrm{mod}\ 8)$ かつ $\eta \in \mathbb Z[\sqrt d]$” または $d \equiv 2,$ $3\ (\mathrm{mod}\ 4)$ であるとき, $S(d)$ は $\mathbb Q(\sqrt d)$ で分解する素数全体からなる.
- (b)
- $d \equiv 5\ (\mathrm{mod}\ 8)$ かつ $\eta \notin \mathbb Z[\sqrt d]$ ならば, $S(d)$ は $\mathbb Q(\sqrt d)$ で分解する素数全体と $2$ からなる.
- (c)
- “$d \equiv 5\ (\mathrm{mod}\ 8)$ かつ $\eta \notin \mathbb Z[\sqrt d]$ かつ $p = 2$” でないとき, 各 $p \in S(d)$ に対して $l_p$ は $\mathbb Q(\sqrt d)$ の類数以下である.
証明
ここでは, (1) のみを証明します (すると, (3)(a) の下記の解説で使う部分も直ちに証明できます).
$K = \mathbb Q(\sqrt d)$ とし, $K$ の整数環を $O_K$ で表すことにします.
$\mathbb Z[\sqrt d]$ のイデアル全体がなすモノイドを $I$ とおき, $I$ における同値関係 $\sim$ を
で定めます (これは $I$ の乗法と両立します).
$K$ のイデアル類群 $Cl_K$ の有限性により, その部分モノイドとみなせる商モノイド $I/\!\sim$ も有限です.
| $\mathfrak a \sim \mathfrak b$ |
| $\iff$ ある $\lambda \in \mathbb Z[\sqrt d]\setminus\{ 0\}$ に対して $\mathfrak b = (\lambda )\mathfrak a$ または $\mathfrak a = (\lambda )\mathfrak b$ |
- 素数 $p$ が $O_K$ において $2$ つの素イデアル $\mathfrak p,$ $\mathfrak p ' = \{\alpha ' \mid \alpha \in \mathfrak p\}$ に分解する, つまり
\[ (p) = \mathfrak p\mathfrak p ' \neq \mathfrak p^2\]
が成り立つとします.
$I/\!\sim$ の有限性により,
を満たす整数 $l,$ $X,$ $Y$ が存在します. ここで, $(\mathfrak p\cap \mathbb Z[\sqrt d])^l$ は原始的 (補足 1 参照) なので, $X,$ $Y$ は互いに素です. さらに, $X^2-dY^2 = \pm p^l$ であり, $p$ は $d$ を割り切らないので, $X,$ $d$ は互いに素です. よって, $|X^2-dY^2| = p^l$ は狭義原始的な整数解をもちます.$(\mathfrak p\cap \mathbb Z[\sqrt d])^l = (X+Y\sqrt d), \quad 0 < l \leqq \# Cl_K$ - 逆を示すため, 整数 $Z > 1$ が $K$ で分解しない素因数 $p$ をもつとします.
$(X,Y)$ を $|X^2-dY^2| = Z$ の整数解とします.
- (i)
- $p$ が $K$ において不分岐であるとき. $O_K$ において, 単項イデアル $(Z)$ は \[ (Z) = (X+Y\sqrt d)(X-Y\sqrt d)\] と分解され, 両辺は $(p)$ で割り切れます. $(p)$ は $(X+Y\sqrt d)$ と $(X-Y\sqrt d)$ の一方を割り切り, $(p)$ の自己共役性により他方も割り切ります. $p = 2$ のとき $d \equiv 3\ (\mathrm{mod}\ 8)$ であることに注意すると, \[ p\,O_K\cap\mathbb Z[\sqrt d] = p\,\mathbb Z[\sqrt d]\] であるので (補足 1 参照), $\mathbb Z[\sqrt d]$ においても $(p)$ は $(X+Y\sqrt d)$ と $(X-Y\sqrt d)$ の両方を割り切ります. よって, $p$ は $X+Y\sqrt d$ を割り切り, $X,$ $Y$ を割り切ります.
- (ii)
- $p$ が $K$ で分岐するとき. $p$ は $d$ を割り切り, よって $dY^2\pm Z = X^2$ も割り切るので, $X$ も割り切ります.
補足 1
- $O_K$ または $\mathbb Z[\sqrt d]$ のイデアル $\mathfrak a \neq (0)$ は, 各素数 $p$ に対して $(p)$ で割り切れないとき, 原始的であるという.
- $2$ は, $d \equiv 1,$ $7\ (\text{mod}\ 8)$ のとき $K$ で分解し, $d \equiv 3,$ $5\ (\text{mod}\ 8)$ のとき $K$ において不分岐であり, $d \equiv 2\ (\text{mod}\ 4)$ のとき $K$ で分岐する. 仮定 “$d \not\equiv 5\ (\mathrm{mod}\ 8)$ または $p \neq 2$” により, $d \not\equiv 1\ (\text{mod}\ 4)$ または $p \neq 2$ のとき $p\,O_K\cap\mathbb Z[\sqrt d] = p\,\mathbb Z[\sqrt d]$ が成り立つことが使える.
最後に, 定理 3 を証明します. ポイントは, 斉次化した方程式の両辺を $\mathbb Q(\sqrt d)$ の整数環で素イデアル分解することです.
定理 3 の証明の概略
引き続き, $K = \mathbb Q(\sqrt d)$ とおき, $K$ の整数環を $O_K$ で表すことにします.
$(x,y) = (X/Z,Y/Z)$ ($X,$ $Y,$ $Z$: 互いに素な整数, $Z \geqq 1$) を
\[ x^2-dy^2 = (-1)^r\]
の有理数解とします.
このとき, $(X,Y)$ は
\[ X^2-dY^2 = (-1)^rZ^2\]
の狭義原始的な整数解になります.
$T$ を $Z$ の素因数全体からなる集合とし, $T(d) = T\cap S(d)$ とおきます.
各 $p \in T$ に対して, $p\mathbb Z$ の上にある $O_K$ の素イデアル $\mathfrak p$ をとり, $\mathfrak p{}' = \{\alpha ' \mid \alpha \in \mathfrak p\}$ とおきます.
各 $p \in T(d)$ に対して $2\,\mathrm{ord}_p(Z)$ を $l_p$ で割った商を $q_p,$ 余りを $r_p$ とおき,
各 $p \in T\setminus T(d)$ に対して $r_p = 2\,\mathrm{ord}_p(Z)$ とおきます.
\[ (\xi _p)(\xi _p') = (p)^{l_p} \quad (p \in T(d))\]
であるので, 等式 $X^2-dY^2 = (-1)^rZ^2$ は $O_K$ における単項イデアルに関する等式として
\[ (X^2-dY^2) = (Z)^2\]
つまり
と表されます.
各 $p \in T$ に対して, $d \equiv 2,$ $3\ (\mathrm{mod}\ 4)$ または $p \neq 2$ のとき, $O_K$ において $(p)$ は
\[ (p) = \mathfrak p\mathfrak p{}' \neq \mathfrak p^2\]
と分解されるので, $(X+Y\sqrt d)$ は $\mathfrak p,$ $\mathfrak p{}'$ のいずれか一方で割り切れます (仮にそうでないとすると, $O_K$ において $(p) = \mathfrak p\mathfrak p{}'$ は $(X+Y\sqrt d)$ を割り切り,
\[ p\,O_K\cap\mathbb Z[\sqrt d] = p\,\mathbb Z[\sqrt d]\]
から $\mathbb Z[\sqrt d]$ においても $(p)$ は $(X+Y\sqrt d)$ を割り切り, $p$ が $X,$ $Y$ を割り切ることになってしまうからです).
同様の議論により, 各 $p \in T(d)$ に対して, $d \equiv 2,$ $3\ (\mathrm{mod}\ 4)$ または $p \neq 2$ のとき, $(\xi _p)$ は $\mathfrak p,$ $\mathfrak p{}'$ のいずれかを割り切るので,
が成り立ちます.
| $(X+Y\sqrt d)(X-Y\sqrt d) = \displaystyle\prod_{p \in T(d)}(\xi _p)^{q_p}(\xi _p')^{q_p}\prod_{p \in T}(p)^{r_p}$ |
| $\{ (\xi _p),(\xi _p')\} = \{\mathfrak p{}^{l_p},\mathfrak p{}'^{l_p}\}$ |
- (i)
- $d \equiv 2,\ 3\ (\mathrm{mod}\ 4)$ または $2 \notin T$ のとき. 定理 4 (3) により $T = T(d)$ であり, $O_K$ のイデアル $(X+Y\sqrt d)$ は, $\xi _p^* \in \{\xi _p,\xi _p'\},$ $\mathfrak p^* \in \{\mathfrak p,\mathfrak p{}'\}$ を用いて \[ (X+Y\sqrt d) = \left(\prod_{p \in T(d)}\xi _p^*{}^{q_p}\right)\prod_{p \in T(d)}\mathfrak p^*{}^{r_p}\] と分解されます. \[\left(\frac{X+Y\sqrt d}{\prod_{p \in T(d)}\xi _p^*{}^{q_p}}\right) = \prod_{p \in T(d)}\mathfrak p^*{}^{r_p}\] は原始的な単項イデアルであるから (右辺において $\mathfrak p^*{}^{r_p}$ は原始的, 補足 2 参照) $O_K$ に一致し, 各 $p \in T(d)$ に対して $r_p = 0$ が成り立ちます. このことと $O_K$ の単数群が \[ O_K^\times = \{\pm\eta ^n \mid n \in \mathbb Z\}\] であることから, \[ X+Y\sqrt d = \pm\eta ^n\prod_{p \in T(d)}\xi _p^*{}^{q_p}\] を満たす整数 $n$ が存在します. 両辺を $Z$ で割り, $n_p = q_p$ とおくと, $x+y\sqrt d$ の表示が得られ, $N(X+Y\sqrt d) = (-1)^rZ^2$ であることから \[ l_pn_p \equiv 0 \pmod 2\] が得られます. $X+Y\sqrt d$ の表示において $\eta \notin \mathbb Z[\sqrt d]$ かつ $Z \equiv 1\ (\mathrm{mod}\ 2)$ のとき $n$ は $3$ の倍数でなければりませんが (補足 2 参照), $x,$ $y$ は有理数であり, $2\eta ^n \in \mathbb Z[\sqrt d]$ であることから, この条件は取り除くことができます.
- (ii)
- 残りの場合にも, $d \equiv 1\ (\mathrm{mod}\ 4)$ のときは \[ O_K = \mathbb Z\left[\dfrac{1+\sqrt d}{2}\right]\] であることから議論が多少難しくなりますが ($n,$ $n_p$ の値の調整が必要), 同様の表示が得られます.
補足 2
- $O_K$ の対ごとに素なイデアル $\mathfrak a_1,$ $\dots,$ $\mathfrak a_r$ に対して, $\prod _{i = 1}^r\mathfrak a_i$ が原始的であるのは, 各イデアル $\mathfrak a_1,$ $\dots,$ $\mathfrak a_r$ が原始的である場合に限る (“$\mathfrak a$ が原始的 $\iff$ $O_K/\mathfrak a$ が巡回群” [3, Corollary 6.30] と中国式剰余の定理による).
- $d$ の値によらず, $\eta ^3 \in \mathbb Z[\sqrt d]$ が成り立つ.
例 4
$x^2-34y^2 = 1$ は基本解 $(x,y) = (35,6)$ をもち, $x^2-34y^2 = -1$ は整数解をもちません.
$\mathbb Q(\sqrt{34})$ の基本単数は $\eta = 35+6\sqrt{34}$ です.
$X^2-34Y^2 = -3^2,$ $X^2-34Y^2 = -5^2,$ $X^2-34Y^2 = -11^2$ はそれぞれ基本解 $(X,Y) = (5,1),$ $(3,1),$ $(27,5)$ をもちます.
\[ X^2-34Y^2 = -(3\cdot 5\cdot 11)^2\]
の原始的な整数解 $(X,Y)$ はある整数 $n$ について
- $X+Y\sqrt d = \pm\eta ^n\cdot (5\pm\sqrt{34})\cdot 5\cdot 11$
- $X+Y\sqrt d = \pm\eta ^n\cdot 3\cdot (3\pm\sqrt{34})\cdot 11$
- $X+Y\sqrt d = \pm\eta ^n\cdot 3\cdot 5\cdot (27\pm5\sqrt{34})$
- $X+Y\sqrt d = \pm\eta ^n\cdot (5\pm\sqrt{34})\cdot (3\pm\sqrt{34})\cdot (27\pm5\sqrt{34})$
§4 おわりに
$10$ 年ほど前に見つけた角の二等分線の問題を無事解決できて, 非常にうれしく思います. 格子点を通る $2$ 直線と角の二等分線は, 工学 (光通信, 建築など) への応用も期待できるのではないかと考えています. 角の三等分線, 空間への拡張についても研究を進めているので, 進展があれば, また成果をご報告したいと思います.
また, 本格的な数学クイズの制作を通して興味深い問題が次々に見つかっているので, そちらについても機会があれば発表したいと思います.
この研究を通して, $2$ 次体の整数論の奥深さと応用の可能性を強く感じました. このように, 代数的整数論を用いて解決できる興味深い問題がまだ身近に眠っているかもしれません. 長文にもかかわらず最後まで読んでいただき, ありがとうございました.
参考文献
- [1]
- Takashi Hirotsu, Rational angle bisectors on the coordinate plane and solutions of Pell's equations, https://arxiv.org/abs/2305.01091
- [2]
- Takashi Hirotsu, Diophantine equation related to angle bisectors and solutions of Pell's equations, https://arxiv.org/abs/2209.10434
- [3]
- 青木昇,『素数と $2$ 次体の整数論』, 数学のかんどころ 15, 共立出版, 2012.
- [4]
- R. D. Carmichael, On the numerical factors of the arithmetic forms $\alpha ^n\pm\beta ^n,$ Ann. of Math., 15 (1913–1914), no. 1/4, 30–48.
- [5]
- K. Conrad, Pell's equation, II, https://api.semanticscholar.org/CorpusID:14314437 (2023 年 11 月 15 日閲覧).
- [6]
- T. Koshy, Pell and Pell-Lucas Numbers with Applications, Springer, New York, 2014.
- [7]
- R. A. Mollin, Quadratics, CRC Press, Boca Raton, FL, 1996.
更新履歴
- 2023/12/20
- 公開
- 2023/12/21
- 一部修正
- 2023/12/22
- §3 の細部を加筆
- 2023/12/27
- 一部修正
- 2024/10/29
- 基本解の定義を改訂
お気づきの点などがありましたら, 以下の連絡先までお願いします.
- 氏 名
- 廣津 孝 (ひろつ たかし)
- メール
