分点の位置ベクトル
分点の位置ベクトル
定理《分点の位置ベクトル》
$m,$ $n$ を正の数とする.
平面上の相異なる $2$ 点 $\mathrm A(\vec a),$ $\mathrm B(\vec b)$ を結ぶ線分 $\mathrm{AB}$ を $m:n$ に内分する点 $\mathrm P(\vec p),$ 外分する点 $\mathrm Q(\vec q)$ の位置ベクトルは, それぞれ
\[\vec p = \frac{n\vec a+m\vec b}{m+n}, \quad \vec q = \frac{-n\vec a+m\vec b}{m-n}\]
である.
問題《平面上の点の重心座標と三角形の面積比》
$\alpha,$ $\beta,$ $\gamma$ を正の数とする.
$\mathrm A(\vec a),$ $\mathrm B(\vec b),$ $\mathrm C(\vec c)$ を結ぶ三角形の内部の点 $\mathrm P(\vec p)$ について, 直線 $\mathrm{AP},$ $\mathrm{BP},$ $\mathrm{CP}$ と辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の交点をそれぞれ $\mathrm D,$ $\mathrm E,$ $\mathrm F$ とおく.
次は同値であることを示せ.
- (i)
- $\alpha\overrightarrow{\mathrm{AP}}+\beta\overrightarrow{\mathrm{BP}}+\gamma\overrightarrow{\mathrm{CP}} = \vec 0$ が成り立つ.
- (ii)
- $\vec p = \dfrac{\alpha\vec a+\beta\vec b+\gamma\vec c}{\alpha +\beta +\gamma}$ である.
- (iii)
- $\triangle\mathrm{BCP}:\triangle\mathrm{CAP}:\triangle\mathrm{ABP} = \alpha :\beta :\gamma$ である.
- (iv)
- $\mathrm{BD}:\mathrm{DC} \!=\! \gamma :\beta,$ $\mathrm{CE}:\mathrm{EA} \!=\! \alpha :\gamma,$ $\mathrm{AF}:\mathrm{FB} \!=\! \beta :\alpha$ である.
- (A)
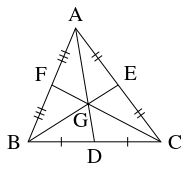
- 重心 $\mathrm G$ の位置ベクトル $\vec g$ は, \[\vec g = \frac{\vec a+\vec b+\vec c}{3}\] である.
- (B)
- 垂心 $\mathrm H$ の位置ベクトル $\vec h$ は, \[\vec h = \frac{(\tan A)\vec a+(\tan B)\vec b+(\tan C)\vec c}{\tan A+\tan B+\tan C}\] である.
- (C)
- 外心 $\mathrm O$ の位置ベクトル $\vec o$ は, \[\vec o = \frac{(\sin 2A)\vec a+(\sin 2B)\vec b+(\sin 2C)\vec c}{\sin 2A+\sin 2B+\sin 2C}\] である.
- (D)
- 内心 $\mathrm I$ の位置ベクトル $\vec i$ は, \[\vec i = \frac{a\vec a+b\vec b+c\vec c}{a+b+c}\] である.
解答例
-
(i) $\iff$ (ii) は,
\[\begin{aligned}
&\alpha\overrightarrow{\mathrm{AP}}+\beta\overrightarrow{\mathrm{BP}}+\gamma\overrightarrow{\mathrm{CP}} = \vec 0 \\
&\iff \alpha (\vec p-\vec a)+\beta (\vec p-\vec b)+\gamma (\vec p-\vec c) = \vec 0 \\
&\iff \vec p = \frac{\alpha\vec a+\beta\vec b+\gamma\vec c}{\alpha +\beta +\gamma}
\end{aligned}\]
から従う.
- (A)
- 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の中点を $\mathrm D,$ $\mathrm E,$ $\mathrm F$ とおく.
このとき,
\[\mathrm{BD}:\mathrm{DC} = \mathrm{CE}:\mathrm{EA} = \mathrm{AF}:\mathrm{FB} = 1:1\]
から, 重心 $\mathrm G$ の位置ベクトル $\vec g$ は
\[\vec g = \frac{\vec a+\vec b+\vec c}{3}\]
である.
- (B)
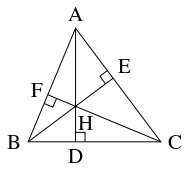
- 頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ から対辺に下ろした垂線の足を $\mathrm D,$ $\mathrm E,$ $\mathrm F$ とおく.
このとき,
\[\begin{aligned}
\mathrm{BD}:\mathrm{DC} &= \frac{\mathrm{AD}}{\tan B}:\frac{\mathrm{AD}}{\tan C} = \tan C :\tan B, \\
\mathrm{CE}:\mathrm{EA} &= \frac{\mathrm{BE}}{\tan C}:\frac{\mathrm{BE}}{\tan A} = \tan A :\tan C, \\
\mathrm{AF}:\mathrm{FB} &= \frac{\mathrm{CF}}{\tan A}:\frac{\mathrm{CF}}{\tan B} = \tan B :\tan A
\end{aligned}\]
から, 垂心 $\mathrm H$ の位置ベクトル $\vec h$ は
\[\vec h = \frac{(\tan A)\vec a+(\tan B)\vec b+(\tan C)\vec c}{\tan A+\tan B+\tan C}\]
である.
- (C)
- 外接円の半径を $R$ とおく.
このとき,
\[\begin{aligned}
&\triangle\mathrm{BCO}:\triangle\mathrm{CAO}:\triangle\mathrm{ABO} \\
&= \frac{1}{2}R^2\sin 2A:\frac{1}{2}R^2\sin 2B:\frac{1}{2}R^2\sin 2C \\
&= \sin 2A:\sin 2B:\sin 2C
\end{aligned}\]
から, 外心 $\mathrm O$ の位置ベクトル $\vec o$ は
\[\vec o = \frac{(\sin 2A)\vec a+(\sin 2B)\vec b+(\sin 2C)\vec c}{\sin 2A+\sin 2B+\sin 2C}\]
である.

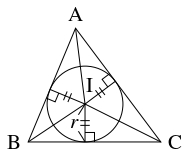
- (D)
- 内接円の半径を $r$ とおく.
このとき,
\[\begin{aligned}
\triangle\mathrm{BCI}:\triangle\mathrm{CAI}:\triangle\mathrm{ABI} &= \frac{1}{2}ar:\frac{1}{2}br:\frac{1}{2}cr \\
&= a:b:c
\end{aligned}\]
から, 内心 $\mathrm I$ の位置ベクトル $\vec i$ は
\[\vec i = \frac{a\vec a+b\vec b+c\vec c}{a+b+c}\]
である.
(ii) $\Longrightarrow$ (iii) を示すため, (ii) を仮定する. \[\vec p = \frac{\alpha\vec a+\beta\vec b+\gamma\vec c}{\alpha +\beta +\gamma} = \frac{\alpha\vec a+(\gamma +\beta )\dfrac{\beta\vec b+\gamma\vec c}{\gamma +\beta}}{(\gamma +\beta )+\alpha}\] であるから, 線分 $\mathrm{BC}$ を $\gamma :\beta$ に内分する点を $\mathrm D$ とおくと, 点 $\mathrm P$ は線分 $\mathrm{AD}$ を $(\gamma +\beta ):\alpha$ に内分する点である.
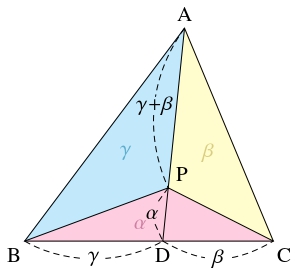
(iii) $\Longrightarrow$ (iv) は, \[\begin{aligned} \triangle\mathrm{ABP}:\triangle\mathrm{CAP} &= \mathrm{BD}:\mathrm{DC}, \\ \triangle\mathrm{BCP}:\triangle\mathrm{ABP} &= \mathrm{CE}:\mathrm{EA}, \\ \triangle\mathrm{CAP}:\triangle\mathrm{BCP} &= \mathrm{AF}:\mathrm{FB} \end{aligned}\] から従う.
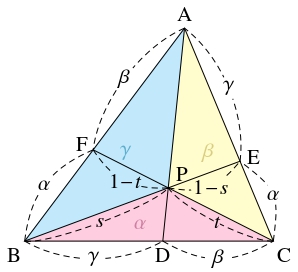
以上から, (i)~(iv) は同値である. 次に, (A)~(D) を示す.
参考
- 本問の結果から, 面積比 \[\triangle\mathrm{BCP}:\triangle\mathrm{CAP}:\triangle\mathrm{ABP} = \alpha :\beta :\gamma\] を用いて $\triangle\mathrm{ABC}$ の内部の点 $\mathrm P$ を表すことができる. この面積比を表す実数の組 $(\alpha,\beta,\gamma )$ を点 $\mathrm P$ の「重心座標」(barycentric coordinates) または「面積座標」(area coordinates) と呼ぶ.
- $\alpha,$ $\beta,$ $\gamma,$ $\delta$ を正の数とする. 四面体 $\mathrm{ABCD}$ の内部の点 $\mathrm P$ について, 四面体 $\mathrm{PQRS}$ の体積を $V_{\mathrm{PQRS}}$ で表すとき, \[\begin{aligned} &\alpha\overrightarrow{\mathrm{AP}}+\beta\overrightarrow{\mathrm{BP}}+\gamma\overrightarrow{\mathrm{CP}}+\delta\overrightarrow{\mathrm{DP}} = \vec 0 \\ &\iff V_{\mathrm{BCDP}}:V_{\mathrm{ACDP}}:V_{\mathrm{ABDP}}:V_{\mathrm{ABCP}} = \alpha :\beta :\gamma:\delta \end{aligned}\] の成り立つことが知られている.
- 本問において, $\triangle\mathrm{ABC}$ の $\angle\mathrm A$ 内の「傍心」の位置ベクトル $\overrightarrow{i_{\mathrm A}}$ は, \[\overrightarrow{i_{\mathrm A}} = \frac{-a\vec a+b\vec b+c\vec c}{-a+b+c}\] と表される.
問題《角の二等分線の性質》
$\triangle\mathrm{ABC}$ において, $\angle\mathrm A$ の内角の二等分線と辺 $\mathrm{BC}$ の交点を $\mathrm D$ とおく.
\[\mathrm{BD}:\mathrm{DC} = \mathrm{AB}:\mathrm{AC}\]
が成り立つことを示せ.
ひし形の対角線が角を二等分することは証明なしに使ってよい.
解答例
$\vec b = \overrightarrow{\mathrm{AB}},$ $\vec c = \overrightarrow{\mathrm{AC}}$ とおく.
$\angle\mathrm{BAC}$ を共有する $1$ 辺の長さが $1$ のひし形を考えると,
$\overrightarrow{\mathrm{AD}}$ は $\dfrac{\vec b}{|\vec b|}+\dfrac{\vec c}{|\vec c|}$ に平行であるから, ある実数 $k$ に対して
\[\overrightarrow{\mathrm{AD}} = k\left(\frac{\vec b}{|\vec b|}+\frac{\vec c}{|\vec c|}\right) = \frac{k}{|\vec b|}\vec b+\frac{k}{|\vec c|}\vec c\]
となる.
点 $\mathrm D$ は辺 $\mathrm{BC}$ 上にあるから,
である.
ゆえに,
\[\overrightarrow{\mathrm{AD}} = \frac{|\vec c|\vec b+|\vec b|\vec c}{|\vec b|+|\vec c|}\]
であるから,
\[\mathrm{BD}:\mathrm{DC} = |\vec b|:|\vec c| = \mathrm{AB}:\mathrm{AC}\]
が成り立つ.
| $\dfrac{k}{|\vec b|}+\dfrac{k}{|\vec c|} = 1$ よって $k = \dfrac{|\vec b||\vec c|}{|\vec b|+|\vec c|}$ |
問題《四角形の幾何学的重心》
平行四辺形でない四角形 $\mathrm A_1\mathrm A_2\mathrm A_3\mathrm A_4$ の向かい合う辺の中点を結ぶ $2$ 本の線分と, 対角線の中点を結ぶ線分は $1$ 点 $\mathrm G$ で交わることを示せ.
解答例
$\mathrm A_k\left(\vec{a_k}\right)$ $(1 \leqq k \leqq 4)$ とおく.
このとき,
\[\begin{aligned}
&\frac{\dfrac{\vec{a_1}+\vec{a_2}}{2}+\dfrac{\vec{a_3}+\vec{a_4}}{2}}{2} = \frac{\dfrac{\vec{a_4}+\vec{a_1}}{2}+\dfrac{\vec{a_2}+\vec{a_3}}{2}}{2} \\
&= \frac{\dfrac{\vec{a_1}+\vec{a_3}}{2}+\dfrac{\vec{a_2}+\vec{a_4}}{2}}{2} = \frac{\vec{a_1}+\vec{a_2}+\vec{a_3}+\vec{a_4}}{4}
\end{aligned}\]
であるから, 辺 $\mathrm A_1\mathrm A_2$ の中点と辺 $\mathrm A_3\mathrm A_4$ の中点を結ぶ線分, 辺 $\mathrm A_4\mathrm A_1$ の中点と辺 $\mathrm A_2\mathrm A_3$ の中点を結ぶ線分, 対角線 $\mathrm A_1\mathrm A_3$ の中点と対角線 $\mathrm A_2\mathrm A_4$ の中点を結ぶ線分は, それぞれの中点 $\mathrm G$ で交わる.
参考
点 $\mathrm G$ は, 四角形 $\mathrm A_1\mathrm A_2\mathrm A_3\mathrm A_4$ の「幾何学的重心」(geometric center) と呼ばれ, 四角形の各辺の中点を結んで得られる平行四辺形の対角線の交点と一致する.
この平行四辺形は「ヴァリニョンの平行四辺形」(Varignon's parallelogram) と呼ばれる.
問題《四角形の物理的重心》
- (1)
- 平行四辺形 $\mathrm A_1\mathrm A_2\mathrm A_3\mathrm A_4$ の向かい合う辺の中点を結ぶ $2$ 本の線分は, 対角線の交点で交わることを示せ.
- (2)
- 四角形 $\mathrm A_1\mathrm A_2\mathrm A_3\mathrm A_4$ の各辺上にその $3$ 等分点を $2$ つずつとり,
隣り合う $2$ 辺の $3$ 等分点を近いものどうし結ぶ直線を $4$ 本引いて, 四角形 $Q$ を描く.
- ①
- $Q$ は平行四辺形であることを示せ.
- ②
- $\triangle\mathrm A_k\mathrm A_{k+1}\mathrm A_{k+2}$ の重心を $\mathrm G_k$ とおく $(1 \leqq k \leqq 4,$ $\mathrm A_5 = \mathrm A_1,$ $\mathrm A_6 = \mathrm A_2).$ 線分 $\mathrm G_1\mathrm G_3,$ $\mathrm G_2\mathrm G_4$ の交点 $\mathrm G$ は $Q$ の対角線の交点と一致することを示せ.
解答例
- (1)
- 対角線の交点 $\mathrm O$ を基点とする位置ベクトルを用いて $\mathrm A_k(\vec{a_k})$ $(1 \leqq k \leqq 4)$ とおく. このとき, \[\begin{aligned} &\frac{\dfrac{\vec{a_1}+\vec{a_2}}{2}+\dfrac{\vec{a_3}+\vec{a_4}}{2}}{2} = \frac{\dfrac{\vec{a_4}+\vec{a_1}}{2}+\dfrac{\vec{a_2}+\vec{a_3}}{2}}{2} \\ &= \frac{\vec{a_1}+\vec{a_2}+\vec{a_3}+\vec{a_4}}{4} = \frac{\dfrac{\vec{a_1}+\vec{a_3}}{2}+\dfrac{\vec{a_2}+\vec{a_4}}{2}}{2} \\ &= \frac{\vec 0+\vec 0}{2} = \vec 0 \end{aligned}\] であるから, 辺 $\mathrm A_1\mathrm A_2$ の中点と辺 $\mathrm A_3\mathrm A_4$ の中点を結ぶ線分, 辺 $\mathrm A_4\mathrm A_1$ の中点と辺 $\mathrm A_2\mathrm A_3$ の中点を結ぶ線分は, それぞれの中点で交わり, その交点は $\mathrm O$ と一致する.
- (2)
- ①
- $\mathrm A_k\left(\vec{a_k}\right)$ $(1 \leqq k \leqq 4),$ $\vec{a_5} = \vec{a_1}$ とおく.
辺 $\mathrm A_k\mathrm A_{k+1}$ を $1:2,$ $2:1$ に内分する点はそれぞれ \[\mathrm B_k\left(\frac{2\vec{a_k}+\overrightarrow{a_{k+1}}}{3}\right),\ \mathrm C_k\left(\frac{\vec{a_k}+2\overrightarrow{a_{k+1}}}{3}\right)\] であるから, 四角形 $Q$ の $1$ 組の向かい合う辺の方向ベクトルは \[\begin{aligned} \overrightarrow{\mathrm C_1\mathrm B_2} = \frac{2\vec{a_2}+\vec{a_3}}{3}-\frac{\vec{a_1}+2\vec{a_2}}{3} &= \frac{\vec{a_3}-\vec{a_1}}{3}, \\ \overrightarrow{\mathrm C_3\mathrm B_4} = \frac{2\vec{a_4}+\vec{a_1}}{3}-\frac{\vec{a_3}+2\vec{a_4}}{3} &= \frac{\vec{a_1}-\vec{a_3}}{3} \end{aligned}\] で, $\overrightarrow{\mathrm A_1\mathrm A_3}$ に平行である. 同様に, もう $1$ 組の向かい合う辺は $\overrightarrow{\mathrm A_2\mathrm A_4}$ に平行である. よって, 四角形 $Q$ は平行四辺形である.
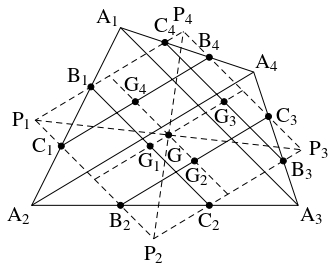
- ②
- \[\begin{aligned} \overrightarrow{\mathrm B_1\mathrm C_2} &= \frac{\vec{a_2}+2\vec{a_3}}{3}-\frac{2\vec{a_1}+\vec{a_2}}{3} = \frac{2\vec{a_3}-2\vec{a_1}}{3} \\ &= \frac{2\vec{a_3}+\vec{a_4}}{3}-\frac{\vec{a_4}+2\vec{a_1}}{3} = \overrightarrow{\mathrm C_4\mathrm B_3} \end{aligned}\] であるから, 線分 $\mathrm B_1\mathrm C_2,$ $\mathrm B_3\mathrm C_4$ は $Q$ の辺に平行であって $Q$ の辺と同じ長さをもつ. さらに, \[\begin{aligned} \frac{1}{2}\left(\frac{2\vec{a_1}+\vec{a_2}}{3}+\frac{\vec{a_2}+2\vec{a_3}}{3}\right) &= \frac{\vec{a_1}+\vec{a_2}+\vec{a_3}}{3}, \\ \frac{1}{2}\left(\frac{2\vec{a_3}+\vec{a_4}}{3}+\frac{\vec{a_4}+2\vec{a_1}}{3}\right) &= \frac{\vec{a_3}+\vec{a_4}+\vec{a_1}}{3} \end{aligned}\] であるから, $\triangle\mathrm A_1\mathrm A_2\mathrm A_3$ の重心 $\mathrm G_1,$ $\triangle\mathrm A_3\mathrm A_4\mathrm A_1$ の重心 $\mathrm G_3$ は, それぞれ線分 $\mathrm B_1\mathrm C_2,$ $\mathrm B_3\mathrm C_4$ の中点と一致する. よって, $\mathrm G_1,$ $\mathrm G_3$ は $Q$ の向かい合う辺の中点を結ぶ直線上にある. 同様に, $\mathrm G_2\mathrm G_4$ は $Q$ の向かい合う辺の中点を結ぶ直線上にある. よって, 線分 $\mathrm G_1\mathrm G_3,$ $\mathrm G_2\mathrm G_4$ の交点 $\mathrm G$ は, $Q$ の向かい合う辺の中点を結ぶ $2$ 本の線分の交点であり, (1) の結果により $Q$ の対角線の交点と一致する.
参考
(2) の点 $\mathrm G$ は四角形 $\mathrm A_1\mathrm A_2\mathrm A_3\mathrm A_4$ の「物理的重心」(physical center of gravity) と呼ばれ, (2) の平行四辺形 $Q$ は「ウィッテンバウアーの平行四辺形」(Wittenbauer's parallelogram) と呼ばれる.
「幾何学的重心」と「物理的重心」は一致するとは限らない.
問題《四面体の幾何学的重心》
四面体において, 頂点とその対面の重心を結ぶ $4$ 本の線分は $1$ 点で交わることを示せ.
解答例
$\mathrm A(\vec a),$ $\mathrm B(\vec b),$ $\mathrm C(\vec c),$ $\mathrm D(\vec d)$ を頂点とする四面体を考える.
頂点 $\mathrm A$ とその対面 $\triangle\mathrm{BCD}$ の重心 $\mathrm G_{\mathrm A}$ の位置ベクトルは,
\[\vec{g_{\mathrm A}} = \frac{\vec b+\vec c+\vec d}{3}\]
である.
線分 $\mathrm{AG}_{\mathrm A}$ を $3:1$ に内分する点 $\mathrm G$ の位置ベクトルは,
\[\vec g = \frac{\vec a+3\vec{g_{\mathrm A}}}{4} = \frac{\vec a+\vec b+\vec c+\vec d}{4}\]
である.
同様に, 他の頂点とその対面の重心を結ぶ線分を $3:1$ に内分する点の位置ベクトルも $\vec g$ であるから,
四面体 $\mathrm{ABCD}$ の頂点とその対面の重心を結ぶ $4$ 本の線分は $1$ 点 $\mathrm G$で交わる.
問題《四面体の内心》
- (1)
- 四面体 $\mathrm{ABCD}$ の体積を $V,$ 四面体 $\mathrm{ABCD}'$ の体積を $V'$ とおく.
次の各場合に, 体積の比 $V:V'$ を求めよ.
- (i)
- $\overrightarrow{\mathrm{AD}'} = d\overrightarrow{\mathrm{AD}}$ のとき.
- (ii)
- $\overrightarrow{\mathrm{AD}'} = b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}}+d\overrightarrow{\mathrm{AD}}$ のとき.
- (2)
- 四面体 $\mathrm{ABCD}$ において, 頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ の各位置ベクトルが $\vec a,$ $\vec b,$ $\vec c,$ $\vec d$ であり, 各対面の面積が $\alpha,$ $\beta,$ $\gamma,$ $\delta$ であるとする. このとき, 位置ベクトルが \[\frac{\alpha\vec a+\beta\vec b+\gamma\vec c+\delta\vec d}{\alpha +\beta +\gamma +\delta}\] である点 $\mathrm I$ と平面 $\mathrm{ABC}$ の距離 $r$ を求めよ.
- (3)
- (2) の点 $\mathrm I$ は四面体 $\mathrm{ABCD}$ の内接球の中心であることを示せ.
(参考: $2017$ 早稲田大)
解答例
- (1)
- (i)
- $\overrightarrow{\mathrm{AD}'} = d\overrightarrow{\mathrm{AD}}$ のとき. 四面体 $\mathrm{ABCD},$ $\mathrm{ABCD}'$ において共通の面 $\mathrm{ABC}$ を底面と見たときの高さの比は \[\mathrm{AD}:\mathrm{AD}' = 1:|d|\] であるから, 体積の比も \[ V:V' = 1:|d|\] である.
- (ii)
- $\overrightarrow{\mathrm{AD}'} = b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}}+d\overrightarrow{\mathrm{AD}}$ のとき. 点 $\mathrm D'$ は $\overrightarrow{\mathrm{AD}_0} = d\overrightarrow{\mathrm{AD}}$ で定まる点 $\mathrm D_0$ を通って面 $\mathrm{ABC}$ に平行な平面上にあるから, この場合の四面体 $\mathrm{ABCD}'$ の体積は (i) の場合に等しい. よって, 求める体積の比は \[ V:V' = 1:|d|\] である.
- (2)
- 位置ベクトルの基点を $\mathrm A$ にとり直すと, $\overrightarrow{\mathrm{AA}} = \vec 0$ から \[\overrightarrow{\mathrm{AI}} = \frac{\beta\overrightarrow{\mathrm{AB}}+\gamma\overrightarrow{\mathrm{AC}}+\delta\overrightarrow{\mathrm{AD}}}{\alpha +\beta +\gamma +\delta}\] が得られる. よって, (1) により四面体 $\mathrm{ABCI}$ の体積は \[\frac{\delta r}{3} = \frac{\delta}{\alpha +\beta +\gamma +\delta}V\] と表される. したがって, 求める距離は \[ r = \frac{3V}{\alpha +\beta +\gamma +\delta} \quad \cdots [1]\] である.
- (3)
- $[1]$ は $\alpha,$ $\beta,$ $\gamma,$ $\delta$ に関する対称式であるから, 点 $\mathrm I$ と平面 $\mathrm{BCD},$ $\mathrm{CDA},$ $\mathrm{DAB}$ の距離はすべて $[1]$ に等しい. ゆえに, $[1]$ は四面体 $\mathrm{ABCD}$ の内接球の半径であるから, 点 $\mathrm I$ はその中心である.
参考
$\mathrm A(\vec a),$ $\mathrm B(\vec b),$ $\mathrm C(\vec c),$ $\mathrm{BC} = a,$ $\mathrm{CA} = b,$ $\mathrm{AB} = c$ であるとき, $\triangle\mathrm{ABC}$ の内心の位置ベクトルは
\[\frac{a\vec a+b\vec b+c\vec c}{a+b+c}\]
である (こちらを参照).
(3) は, この高次元化である.
