$2$ 次曲線の内外に接する多角形
チャップル=オイラーの定理
定理《チャップル=オイラーの定理》
三角形の外心を $\mathrm O,$ 内心を $\mathrm I,$ 外接円の半径を $R,$ 内接円の半径を $r$ とおくと,
\[\mathrm{OI}^2 = R^2-2Rr\]
が成り立つ.
証明
こちらを参照.
ポンスレの閉形定理
定理《ポンスレの閉形定理》
$2$ 次曲線 $C,$ $D$ に対して, $C$ に内接し, $D$ に外接する $n$ 角形が $1$ つでも存在するならば,
$C$ 上の任意の点 $\mathrm P_1$ を $1$ つの頂点とし, $C$ に内接し, $D$ に外接する $n$ 角形が存在する.
つまり, 点 $\mathrm P_k$ から $D$ に引いた接線と $C$ の交点 $(\neq \mathrm P_k)$ を $\mathrm P_{k+1}$ とおくことで点 $\mathrm P_2$ $\cdots,$ $\mathrm P_n,$ $\mathrm P_{n+1}$ を順次定めると,
$\mathrm P_{n+1} = \mathrm P_1$ となり, $C$ に内接し, $D$ に外接する $n$ 角形 $\mathrm P_1\mathrm P_2\cdots \mathrm P_n$ が得られる.
高校数学の問題
図形と計量
問題《チャップル=オイラーの定理》
次のことを示せ.
- (1)
- 点 $\mathrm O$ を中心とする半径 $R$ の円周の弦 $\mathrm{XY}$ 上のすべての点 $\mathrm P$ に対して
\[\mathrm{OP}^2 = R^2-\mathrm{XP}\cdot\mathrm{YP}\]
が成り立つ.
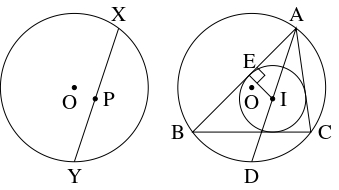
- (2)
- $\triangle\mathrm{ABC}$ の外心を $\mathrm O,$ 外接円の半径を $R,$ 内心を $\mathrm I,$ 内接円の半径を $r$ とおく.
さらに, 直線 $\mathrm{AI}$ と円周 $\mathrm O$ の交点のうち $\mathrm A$ と異なる方の点を $\mathrm D$ とおき, 辺 $\mathrm{AB}$ と円周 $\mathrm I$ の接点を $\mathrm E$ とおく.
このとき,
- ①
- $\mathrm{DB} = \mathrm{DI}$
- ②
- $\mathrm{AI}\cdot\mathrm{DB} = 2Rr$
- ③
- $\mathrm{OI}^2 = R^2-2Rr$
- ④
- $R \geqq 2r$
- (3)
- (2) の円周 $\mathrm O$ の上に点 $\mathrm P_1$ をとり, 直線 $\mathrm P_1\mathrm I$ と円周 $\mathrm O$ の交点のうち $\mathrm P_1$ と異なる方の点を $\mathrm P'_1$ とおく. さらに, $\mathrm I$ を通って $\mathrm P'_1$ を中心とする円周と円周 $\mathrm O$ の交点を $\mathrm P_2,$ $\mathrm P_3$ とおく. このとき, $\triangle\mathrm P_1\mathrm P_2\mathrm P_3$ の内心は $\mathrm I$ と一致する.
(参考: $2012$ 宮崎大)
解答例
こちらを参照.
図形と方程式
問題《ポンスレの閉形定理にまつわる問題》
原点を中心とする半径 $1$ の円周 $C$ と放物線 $D:y = x^2-2$ について, 次の問いに答えよ.
- (A)
- $D$ の頂点 $\mathrm R(0,-2)$ から $C$ に引いた接線と $D$ の交点で $\mathrm R$ と異なるものを $\mathrm P,$ $\mathrm Q$ とおく. このとき, 直線 $\mathrm{PQ}$ も $C$ に接することを示せ.
- (B)
- $D$ 上の相異なる $3$ 点 $\mathrm P(p,p^2-2),$ $\mathrm Q(q,q^2-2),$ $\mathrm R(r,r^2-2)$ に対して, 直線 $\mathrm{PR},$ $\mathrm{QR}$ が原点を中心とする半径 $1$ の円周 $C$ に接するならば, 直線 $\mathrm{PQ}$ も円周 $C$ に接することを示せ.
(参考: $1988$ 名古屋大)
解答例
こちらを参照.