$2$ 次関数
$2$ 次関数のグラフ
定義《$2$ 次関数》
実数の定数 $a,$ $b,$ $c$ $(a \neq 0)$ を用いて $f(x) = ax^2+bx+c$ の形に表される関数を $x$ の $2$ 次関数(quadratic function) と呼ぶ.
問題《$2$ 次関数のグラフの相似性》
どのような $2$ つの $2$ 次関数のグラフも互いに相似であることを示せ.
解答例
すべての $2$ 次関数のグラフが放物線 $y = x^2$ に相似であることを示せば十分である.
$y = x^2$ を原点を基準に $\dfrac{1}{a}$ 倍 $(a > 0)$ に拡大・縮小すると, $y = x^2$ 上の点 $(x,y)$ がうつされる点 $(X,Y)$ は $X = \dfrac{x}{a},$ $Y = \dfrac{y}{a}$ つまり $x = aX,$ $y = aY$ を満たすから,
を満たす.
よって, $y = x^2$ は $y = ax^2$ に相似である.
すべての $2$ 次関数のグラフは, $y = ax^2$ $(a > 0)$ を平行移動, 対称移動したものであるから, $y = x^2$ に相似である.
ゆえに, どのような $2$ つの $2$ 次関数のグラフも互いに相似である.
| $aY = (aX)^2$ つまり $Y = aX^2$ |
参考
一般に, 離心率の等しい $2$ つの $2$ 次曲線は互いに相似であることが知られている.
$2$ 次関数の最大・最小
定理《$2$ 次関数の最大・最小》
$2$ 次関数 $f(x) = a(x-p)^2+q$ ($a,$ $p,$ $q$: 定数, $a \neq 0$) の定義域に $x = p$ が含まれるとき,
- (1)
- $a > 0$ であるならば, $f(x)$ は $x = p$ において最小値をとる.
- (2)
- $a < 0$ であるならば, $f(x)$ は $x = p$ において最大値をとる.
証明
$x^2 \geqq 0$ と $x^2 = 0 \iff x = 0$ から従う.
問題《鉛直投げ上げの最高点の高さ》
時刻 $0$ に, 高さ $0$ の地点から鉛直方向 (水平面に垂直な方向) に初速 $v_0$ (時刻 $0$ におけるの速さ) で物体を投げ上げるとき,
時刻 $t$ における物体の高さ $y$ は, ある正の数 $g$ を用いて
\[ y = v_0t-\frac{1}{2}gt^2\]
と表されるという.
物体が最高点に到達するときの時刻と高さを求めよ.
解答例
$y = v_0t-\dfrac{1}{2}gt^2$ は
\[\begin{aligned}
y &= -\frac{1}{2}g\left( t^2-\frac{2v_0}{g}t\right) \\
&= -\frac{1}{2}g\left( t-\frac{v_0}{g}\right) ^2+\frac{v_0{}^2}{2g}
\end{aligned}\]
と変形できるから, 物体が最高点に到達するときの時刻は $t = \dfrac{v_0}{g},$ 高さは $y = \dfrac{v_0{}^2}{2g}$ である.
参考
古典力学において, 鉛直方向に物体を投げたときの運動を「鉛直投射」(vertical motion) と呼び, 投げる方向によって「鉛直投げ上げ」(vertical throw up), 「鉛直投げ下ろし」(vertical throw down) と呼ぶ.
上記の公式において, 定数 $g$ を「重力加速度」(gravitational acceleration) と呼ぶ.
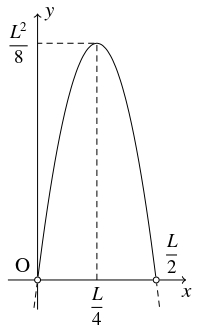
問題《コの字型のレールの断面積の最大値》
横幅が $L$ の長方形の金属板を, 両端から長さの等しい位置 $2$ か所で直角に折り曲げて, 断面が長方形状のレールを作る.
このとき, レールの溝の断面積の最大値を求めよ.
解答例
折り曲げる部分の長さを $x,$ 溝の断面積を $y$ とおく.
底の幅は $L-2x$ で, $x > 0,$ $L-2x > 0$ であるから,
\[ 0 < x < \frac{L}{2}\]
である.
\[\begin{aligned}
y &= x(L-2x) \\
&= -2x^2+Lx \\
&= -2\left( x-\frac{L}{4}\right) ^2+\frac{L^2}{8}
\end{aligned}\]
であるから, $y$ は $x = \dfrac{L}{4}$ のとき最大値 $\dfrac{L^2}{8}$ をとる.
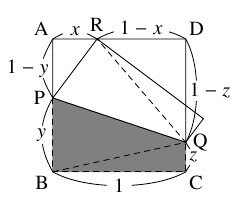
問題《紙を折った部分の面積の最小値》
$1$ 辺の長さが $1$ の正方形の紙 $\mathrm{ABCD}$ を, 頂点 $\mathrm B$ が辺 $\mathrm{AD}$ 上にくるように折るとき,
折り返した部分の面積 $S$ が最小になるのはどのような折り方をした場合か答えよ.
また, その最小値を求めよ.
解答例
辺 $\mathrm{AB}$ 上の点 $\mathrm P$ と辺 $\mathrm{CD}$ 上の点 $\mathrm Q$ を結ぶ線分で折った後に頂点 $\mathrm B$ が辺 $\mathrm{AD}$ 上の点 $\mathrm R$ に移るとして,
$x = \mathrm{AR},$ $y = \mathrm{BP},$ $z = \mathrm{CQ}$ とおく.
このとき,
\[\mathrm{BP} = \mathrm{RP}, \quad \mathrm{BQ} = \mathrm{RQ}\]
である.
$\triangle\mathrm{APR},$ $\triangle\mathrm{BCQ},$ $\triangle\mathrm{DQR}$ に三平方の定理を適用すると,
\[\begin{aligned}
\mathrm{AP}^2+\mathrm{AR}^2 &= \mathrm{PR}^2, \\
\mathrm{BC}^2+\mathrm{CQ}^2 &= \mathrm{BQ}^2 = \mathrm{RQ}^2 = \mathrm{DQ}^2+\mathrm{DR}^2
\end{aligned}\]
から
\[ (1-y)^2+x^2 = y^2, \quad 1^2+z^2 = (1-z)^2+(1-x)^2\]
となるので,
\[ y = \frac{x^2+1}{2}, \quad z = \frac{x^2-2x+1}{2}\]
である.
よって, 折り返した部分の台形 $\mathrm{PBCQ}$ の面積 $S$ は,
\[\begin{aligned}
S &= \frac{1}{2}(y+z)\cdot 1 \\
&= \frac{1}{2}\left(\frac{x^2+1}{2}+\frac{x^2-2x+1}{2}\right) \\
&= \frac{1}{2}(x^2-x+1) \\
&= \frac{1}{2}\left( x-\frac{1}{2}\right) ^2+\frac{3}{8}
\end{aligned}\]
と表される.
$0 \leqq x \leqq 1$ であるから, $S$ は $x = \dfrac{1}{2}$ のとき最小値 $\dfrac{3}{8}$ をとる.
ゆえに, $S$ が最小になるのは頂点 $\mathrm B$ が辺 $\mathrm{AD}$ の中点にくる場合で, その最小値は $\dfrac{3}{8}$ である.