三角形・三角比
三角形
問題《線分を折り曲げてできる三角形》
$1$ 辺の長さが $1$ の線分を $2$ 点で折り曲げ, 端点をつなぐことにより, $3$ 辺の長さが $a,$ $b,$ $c$ の三角形を作る.
次のことを示せ.
- (1)
- 三角形の形状によらず, $a,$ $b,$ $c < \dfrac{1}{2}$ である.
- (2)
- $a = b$ のとき, $a = b > \dfrac{1}{4}$ である.
- (3)
- $a,$ $b > 1-\dfrac{1}{\sqrt 2}$ のとき, 長さが $a,$ $b$ の辺が挟む角は鋭角である.
解答例
- (1)
- 三角形ができるためには \[ a < b+c\] であることが必要である. この不等式に $a+b+c = 1$ から得られる $c = 1-a-b$ を代入すると \[ a < b+(1-a-b)\] となるから, $2a < 1$ つまり $a < \dfrac{1}{2}$ が成り立つ. 同様に, $b,$ $c < \dfrac{1}{2}$ も成り立つ.
- (2)
- $a = b$ のとき, $c < a+b$ に $c = 1-2a$ を代入すると \[ 1-2a < a+a\] となるから, $4a > 1$ よって $a = b > \dfrac{1}{4}$ が成り立つ.
- (3)
- $a,$ $b > 1-\dfrac{1}{\sqrt 2}$ のとき, $1-a,$ $1-b < \dfrac{1}{\sqrt 2}$ と $c = 1-a-b$ から \[\begin{aligned} &a^2+b^2-c^2 = (a^2+b^2)-(1-a-b)^2 \\ &= (a^2+b^2)-(1+a^2+b^2-2a-2b+2ab) \\ &= -1+2a+2b-2ab = 1-2(1-a-b+ab) \\ &= 1-2(1-a)(1-b) \\ &> 1-2\cdot\frac{1}{\sqrt 2}\cdot\frac{1}{\sqrt 2} = 0 \end{aligned}\] となり, $c^2 < a^2+b^2$ となるので, 長さが $a,$ $b$ の辺が挟む角は鋭角である.
三角比
問題《単位正三角形に内接する正方形》
$1$ 辺の長さが $1$ の正三角形に $1$ 辺と $2$ つの頂点が接するような正方形の $1$ 辺の長さ, 面積を求めよ.
解答例
$1$ 辺の長さが $1$ の正三角形は, $1$ 辺の長さが $x$ の正方形, $1$ 辺の長さが $x$ の正三角形, および正三角形を二等分した形の直角三角形 $2$ 個に分けられる (図は省略).
この直角三角形において斜辺の長さは $1-x,$ $60^\circ$ の角の対辺の長さは $x$ であるから,
が成り立つ.
よって,
から, 求める正方形の $1$ 辺の長さは
\[ x = \frac{\sqrt 3}{2+\sqrt 3} = \sqrt 3(2-\sqrt 3) = 2\sqrt 3-3,\]
面積は
\[ x^2 = (2\sqrt 3-3)^2 = 21-12\sqrt 3\]
である.
| $\sin 60^\circ = \dfrac{x}{1-x}$ つまり $\dfrac{x}{1-x} = \dfrac{\sqrt 3}{2}$ |
| $2x = \sqrt 3(1-x)$ つまり $(2+\sqrt 3)x = \sqrt 3$ |
問題《$18^\circ$ と $36^\circ$ の三角比》
$1$ 辺の長さが $1$ の正五角形 $\mathrm{ABCDE}$ において, 対角線 $\mathrm{AC},$ $\mathrm{BD}$ の交点を $\mathrm P$ とおく.
- (1)
- $\angle\mathrm{CAD},$ $\angle\mathrm{ACD}$ の大きさを求めよ.
- (2)
- $\triangle\mathrm{ACD},$ $\triangle\mathrm{DCP}$ は相似であることを示せ.
- (3)
- 線分 $\mathrm{CP},$ 対角線 $\mathrm{AC}$ の長さを求めよ.
- (4)
- $\cos 18^\circ,$ $\sin 18^\circ,$ $\tan 18^\circ$ の値を求めよ.
- (5)
- $\cos 36^\circ,$ $\sin 36^\circ,$ $\tan 36^\circ$ の値を求めよ.
解答例
- (1)
- \[\angle\mathrm{ABC} = (5-2)\times 180^\circ\div 5 = 108^\circ\] で, $\triangle\mathrm{ABC}$ は $\mathrm{BA} = \mathrm{BC}$ なる二等辺三角形であるから, \[\angle\mathrm{BAC} = \angle\mathrm{BCA} = (180^\circ -108^\circ )\div 2 = 36^\circ\] である. $\triangle\mathrm{ABC} \equiv \triangle\mathrm{DEA} \equiv \triangle\mathrm{EAB}$ から \[\angle\mathrm{EAD} = \angle\mathrm{BCA} = 36^\circ, \quad \angle\mathrm{EAB} = \angle\mathrm{ABC} = 108^\circ\] であるので, \[\begin{aligned} \angle\mathrm{CAD} &= \angle\mathrm{EAB}-\angle\mathrm{BAC}-\angle\mathrm{EAD} \\ &= 108^\circ-36^\circ -36^\circ = 36^\circ \end{aligned}\] である. さらに, $\triangle\mathrm{ABC} \equiv \triangle\mathrm{BCD}$ から \[\angle\mathrm{BCD} = \angle\mathrm{ABC} = 108^\circ\] であるので, \[\angle\mathrm{ACD} = \angle\mathrm{BCD}-\angle\mathrm{BCA} = 108^\circ-36^\circ = 72^\circ\] である.
- (2)
- 明らかに \[\angle\mathrm{DCP} = \angle\mathrm{ACD} = 72^\circ\] であり, $\triangle\mathrm{ABC} \equiv \triangle\mathrm{BCD}$ から \[\angle\mathrm{CDP} = \angle\mathrm{CDB} = \angle\mathrm{BCA} = 36^\circ = \angle\mathrm{CAD}\] であるので, $\triangle\mathrm{ACD},$ $\triangle\mathrm{DCP}$ は相似である.
- (3)
- $x = \mathrm{CP}$ とおく. $\angle\mathrm{PAD} = \angle\mathrm{PDA} = 36^\circ,$ $\angle\mathrm{DPC} = \angle\mathrm{DCP} = 72^\circ$ から, \[\mathrm{AP} = \mathrm{PD} = \mathrm{CD} = 1\] である. よって, (2) の結果から \[\begin{aligned} \mathrm{AC}:\mathrm{CD} &= \mathrm{DC}:\mathrm{CP} \\ (1+x):1 &= 1:x \\ (1+x)x &= 1^2 \\ x^2+x-1 &= 0 \end{aligned}\] が成り立つので, $x > 0$ に注意すると \[\begin{aligned} \mathrm{CP} &= x = \frac{-1+\sqrt 5}{2}, \\ \mathrm{AC} &= 1+x = \frac{1+\sqrt 5}{2} \end{aligned}\] が得られる.
- (4)
- 頂点 $\mathrm D$ から対角線 $\mathrm{AC}$ に下ろした垂線の足を $\mathrm H$ とおく. 直角三角形 $\mathrm{CDH}$ に着目すると, \[\begin{aligned} \sin 18^\circ &= \frac{\mathrm{CH}}{\mathrm{CD}} = \frac{\mathrm{CP}\div 2}{\mathrm{CD}} = \frac{x\div 2}{1} \\ &= \frac{1}{2}\cdot\frac{-1+\sqrt 5}{2} = \frac{-1+\sqrt 5}{4} \end{aligned}\] が得られる. よって, \[\begin{aligned} \cos 18^\circ &= \sqrt{1-\sin ^2 18^\circ} = \sqrt{1-\left(\frac{-1+\sqrt 5}{4}\right) ^2} \\ &= \sqrt{\frac{4^2-(-1+\sqrt 5)^2}{4^2}} = \frac{\sqrt{16-(6-2\sqrt 5)}}{4} \\ &= \frac{\sqrt{10+2\sqrt 5}}{4} \end{aligned}\] であり, 辺々を割ると \[\begin{aligned} &\tan 18^\circ = \frac{\sin 18^\circ}{\cos 18^\circ} = \frac{-1+\sqrt 5}{4}\div\frac{\sqrt{10+2\sqrt 5}}{4} \\ &= \frac{(-1+\sqrt 5)\sqrt{10+2\sqrt 5}}{(\sqrt{10+2\sqrt 5})^2} = \frac{(-1+\sqrt 5)\sqrt{10+2\sqrt 5}}{10+2\sqrt 5} \\ &= \frac{(-1+\sqrt 5)(10-2\sqrt 5)\sqrt{10+2\sqrt 5}}{(10+2\sqrt 5)(10-2\sqrt 5)} \\ &= \frac{(-20+12\sqrt 5)\sqrt{10+2\sqrt 5}}{80} = \frac{(-5+3\sqrt 5)\sqrt{10+2\sqrt 5}}{20} \\ &= \frac{\sqrt{(-5+3\sqrt 5)^2(10+2\sqrt 5)}}{20} = \frac{\sqrt{(70-30\sqrt 5)(10+2\sqrt 5)}}{20} \\ &= \frac{\sqrt{400-160\sqrt 5}}{20} = \frac{\sqrt{25-10\sqrt 5}}{5} \end{aligned}\] が得られる.
- (5)
- 点 $\mathrm P$ から対角線 $\mathrm{AD}$ に下ろした垂線の足を $\mathrm K$ とおく. 直角三角形 $\mathrm{AKP}$ に着目すると, \[\begin{aligned} \cos 36^\circ &= \frac{\mathrm{AK}}{\mathrm{AP}} = \frac{\mathrm{AD}\div 2}{\mathrm{AP}} = \frac{(1+x)\div 2}{1} \\ &= \frac{1}{2}\cdot\frac{1+\sqrt 5}{2} = \frac{1+\sqrt 5}{4} \end{aligned}\] が得られる. よって, \[\begin{aligned} \sin 36^\circ &= \sqrt{1-\cos ^2 36^\circ} = \sqrt{1-\left(\frac{1+\sqrt 5}{4}\right) ^2} \\ &= \sqrt{\frac{4^2-(1+\sqrt 5)^2}{4^2}} = \frac{\sqrt{16-(6+2\sqrt 5)}}{4} \\ &= \frac{\sqrt{10-2\sqrt 5}}{4} \end{aligned}\] であり, 辺々を割ると \[\begin{aligned} &\tan 36^\circ = \frac{\sin 36^\circ}{\cos 36^\circ} = \frac{\sqrt{10-2\sqrt 5}}{4}\div\frac{1+\sqrt 5}{4} \\ &= \frac{(\sqrt 5-1)\sqrt{10-2\sqrt 5}}{(\sqrt 5+1)(\sqrt 5-1)} = \frac{\sqrt{(\sqrt 5-1)^2(10-2\sqrt 5)}}{4} \\ &= \frac{\sqrt{(6-2\sqrt 5)(10-2\sqrt 5)}}{4} = \frac{\sqrt{80-32\sqrt 5}}{4} \\ &= \sqrt{5-2\sqrt 5} \end{aligned}\] が得られる.
問題《カラビの三角形》
$\angle\mathrm A > 90^\circ,$ $\mathrm{AB} = \mathrm{AC} = 1$ なる三角形 $\mathrm{ABC}$ と, 互いに合同な $2$ つの正方形 $\mathrm{PQRS},$ $\mathrm{ATUV}$ がある.
頂点 $\mathrm P,$ $\mathrm T$ は辺 $\mathrm{AB}$ 上に, 辺 $\mathrm{QR}$ と頂点 $\mathrm U$ は辺 $\mathrm{BC}$ 上に, 頂点 $\mathrm S$ は辺 $\mathrm{AC}$ 上にあるとする.
$\angle\mathrm{ABC} = \theta,$ $x = \mathrm{BC},$ $y = \mathrm{AP}$ とおく.
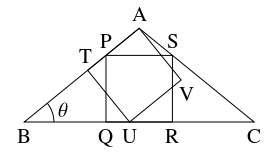
- (1)
- 正方形 $\mathrm{PQRS}$ に着目することで, $\cos\theta,$ $\sin\theta$ を用いて $x,$ $y$ を表す式を導け.
- (2)
- 正方形 $\mathrm{ATUV}$ に着目することで, $\cos\theta,$ $\sin\theta$ を用いて $y$ を表す式を導け.
- (3)
- $x$ を解にもつ整数係数 $3$ 次方程式を $1$ つ求めよ.

解答例
正方形 $\mathrm{PQRS},$ $\mathrm{ATUV}$ の $1$ 辺の長さを $l$ とおく.
- (1)
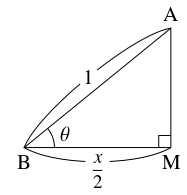
- 点 $\mathrm A$ から $\mathrm{BC},$ $\mathrm{PS}$ に下ろした垂線の足をそれぞれ $\mathrm M,$ $\mathrm N$ とおく.
直角三角形 $\mathrm{ABM}$ に着目すると
\[ x = 2\cos\theta \quad \cdots [1]\]
が得られる.
直角三角形 $\mathrm{APN},$ $\mathrm{PBQ}$ に着目すると \[ l = 2y\cos\theta = (1-y)\sin\theta \quad \cdots [2]\] から \[ y = \frac{\sin\theta}{\sin\theta + 2\cos\theta} \quad \cdots [3]\] が得られる.
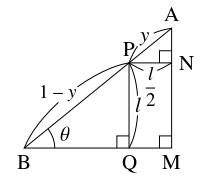
- (2)
- 直角三角形 $\mathrm{UBT}$ に着目すると, $[2]$ から
\[\tan\theta = \frac{l}{1-l} = \frac{2y\cos\theta}{1-2y\cos\theta},\]
よって
\[\begin{aligned}
\tan\theta (1-2y\cos\theta ) &= 2y\cos\theta \\
\tan\theta -2y\sin\theta &= 2y\cos\theta,
\end{aligned}\]
つまり
\[ y = \frac{\tan\theta}{2(\sin\theta +\cos\theta )} = \frac{\sin\theta}{2\cos\theta (\sin\theta +\cos\theta )} \quad \cdots [4]\]
が得られる.
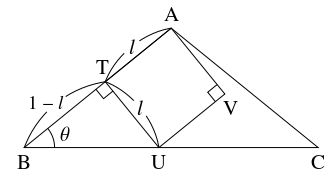
- (3)
- $[2],$ $[4]$ から \[\begin{aligned} \frac{\sin\theta}{\sin\theta + 2\cos\theta} &= \frac{\sin\theta}{2\cos\theta (\sin\theta +\cos\theta )} \\ 2\cos\theta (\sin\theta +\cos\theta ) &= \sin\theta + 2\cos\theta \quad (\because\sin\theta \neq 0) \end{aligned}\] が得られ, 整理した \[\sin\theta (2\cos\theta -1) = 2\cos\theta (1-\cos\theta )\] の両辺を $2$ 乗すると $\cos ^2\theta +\sin ^2\theta = 1$ から \[ (1-\cos ^2\theta )(2\cos\theta -1)^2 = 4\cos ^2\theta (1-\cos\theta )^2\] が得られる. $[1]$ から $\cos\theta = \dfrac{x}{2}$ であるので, \[\begin{aligned} \left( 1-\frac{x^2}{4}\right) (x-1)^2 &= x^2\left( 1-\frac{x}{2}\right) ^2 \\ (4-x^2)(x-1)^2 &= x^2(2-x)^2 \\ \end{aligned}\] つまり \[\begin{aligned} x^2(2-x)^2+(x^2-4)(x-1)^2 &= 0 \\ x^2(x-2)^2+(x+2)(x-2)(x-1)^2 &= 0 \\ (x-2)\{ x^2(x-2)+(x+2)(x-1)^2\} &= 0 \\ (x-2)\{ x^2(x-2)+(x+2)(x^2-2x+1)\} &= 0 \\ (x-2)(2x^3-2x^2-3x+2) &= 0 \\ \end{aligned}\] であり, 三角形の成立条件により $x \neq 2$ であることから \[ 2x^3-2x^2-3x+2 = 0\] である.
参考
- 正三角形の他に, 内接する最大の正方形が $3$ 通りの方法で配置できるような三角形 (鈍角二等辺三角形) がただ $1$ つ存在する.
この三角形を「カラビの三角形」(Calabi's triangle) と呼ぶ.
上記の問題の三角形は, 二等辺三角形の対称性により内接する最大の正方形が $3$ 通りの方法で配置できるから,「カラビの三角形」である.
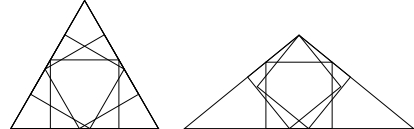
- 「カラビの三角形」における等辺に対する底辺の長さの比 $x$ は, $3$ 次方程式 \[ 2x^3-2x^2-3x+2 = 0\] の $3$ つの実数解のうち最大の解であり,「カルダーノの公式」(こちらを参照) により \[ x = \frac{1}{3}\left( 1+\sqrt[3]{-\frac{23}{4}+\frac{3}{4}\sqrt{237}i}+\sqrt[3]{-\frac{23}{4}-\frac{3}{4}\sqrt{237}i}\right)\] と表され,「カラビの三角形定数」と呼ばれる. その近似値は \[ x = 1.55138\cdots\] であり (こちらを参照),「カラビの三角形」の鋭角, 鈍角の大きさの近似値はそれぞれ \[ 39.13202\cdots ^\circ, \quad 101.73594\cdots ^\circ\] である.
