こんにちは.
廣津孝です.
皆さんとともに数学を通してクリスマスのお祝いができることを大変うれしく思います.
まずご報告ですが, 昨年 ($2023$ 年) の記事, 一昨年 ($2022$ 年) の記事でご紹介した, 座標平面における
どのような有理数 $a,$ $b$ に対して, 傾きが $a,$ $b$ である $2$ 直線のなす角の二等分線の傾きは有理数になるか
日曜数学アドベントカレンダーで記事を書いたことが論文のブラッシュアップにつながりました.
この場を借りて感謝の意をお伝えさせていただきます.
- ※1:
- $2023$ 年の記事執筆後にこのように命名しました.
- ※2:
- ペル方程式の整数解については $6$ 日目のあにりんさんの記事をご覧ください.
- ※3:
- いずれに対しても完全な解決が得られました.
近年筆者は, 次の命題 1 (高校数学の範囲で証明できますが, 一応オリジナルの結果です) を一般化して, いくつかの定理を証明しました.
高校数学でおなじみの場合の数の問題として, $2$ 方向の平行な直線のなす有限集合において $4$ 本の直線で囲まれた平行四辺形の総数を求める問題があります.
命題 1 は, それをアレンジする中で生まれた結果で, 感覚的には, 正方形の辺と平行な辺をもつ「標準大のミニチュア」(定義 3 を参照) の面積がもとの面積の $10$ 分の $1$ であることを意味します.
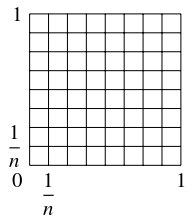
$1$ 辺の長さが $1$ の正方形において, 各辺を $n$ 等分する点 ($n > 1$: 整数) をとり, 向かい合う $2$ 辺の等分点を通って辺に平行な直線 $2(n-1)$ 本を引いたとき, もとの正方形の辺やこれらの直線が囲む小正方形すべてにわたる面積の平均値を $a_n$ とする.
このとき,
| $\lim\limits_{n \to \infty}a_n = \dfrac{1}{10}$ |
である.
【命題 1 の証明の概略】
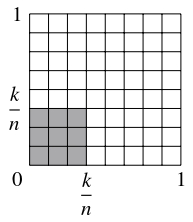
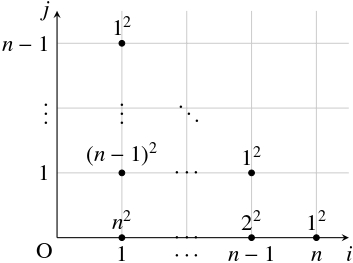
上記のように $2(n-1)$ 本の直線を引いたとき $1$ 辺の長さが $\dfrac{k}{n}$ の小正方形が $(n+1-k)^2$ 個できることから (下図を参照), 和の公式
\[\begin{aligned}
\sum_{k = 1}^nk^2 &= \frac{1}{6}n(n+1)(2n+1), \\
\sum_{k = 1}^nk^3 &= \frac{1}{4}n^2(n+1)^2, \\
\sum_{k = 1}^nk^4 &= \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1)
\end{aligned}\]
により
\[\begin{aligned}
a_n &= \frac{\displaystyle\sum_{k = 1}^n(n-k+1)^2\left(\frac{k}{n}\right) ^2}{\displaystyle\sum_{k = 1}^n(n-k+1)^2} \\
&= \cdots \\
&= \frac{(n+2)(n^2+2n+2)}{5n^2(2n+1)}
\end{aligned}\]
であることがわかるので (詳細は
こちらを参照),
\[ a_n = \frac{\left( 1+\dfrac{2}{n}\right)\left( 1+\dfrac{2}{n}+\dfrac{2}{n^2}\right)}{5\left( 2+\dfrac{1}{n}\right)} \to \frac{1}{10} \quad (n \to \infty ) \]
が得られます.
■
命題 1 の極限値 $\dfrac{1}{10}$ の正体は何なのか, 出所を知るために, その高次元化を考えます.
図形の対象を一般化すると問題の意味がより明確になるので, 多角形, 多面体の一般化である「ポリトープ」, 格子多角形の一般化である「格子ポリトープ」「有理ポリトープ」という概念を用いて,「ミニチュア」の概念を導入します.
以下, $\mathbb Z,$ $\mathbb Q,$ $\mathbb R$ をそれぞれ整数全体のなす集合, 有理数全体のなす集合, 実数全体のなす集合とし, $d$ を正の整数とします.
- (1)
- $\varnothing \neq S \subset \mathbb R^d$ とする.
| $S$ に属する相異なる $2$ 点を結ぶ線分はすべて $S$ に含まれる |
が成り立つとき, $S$ を ($d$ 次元) 凸集合 (convex set) と呼ぶ.
- (2)
- $S \neq \varnothing$ を $\mathbb R^d$ に属する有限個の点の集合とする.
を $S$ の元を頂点とする ($d$ 次元) 凸ポリトープ (convex polytope) と呼ぶ.
本稿では単に ($d$ 次元) ポリトープと呼ぶことにする.
集合 $X$ に対して, $X^d$ は $d$ 個の $X$ の直積で, $X$ に属する $d$ 個の元の組全体からなる集合を表します.
特に, $\mathbb R^2$ は座標平面, $\mathbb R^3$ は座標空間を表します.
多角形, 多面体にのみ興味がある方は, $2$ 次元ポリトープが多角形, $3$ 次元ポリトープが多面体であると理解してもらえれば大丈夫です.
本稿では, 次のようなポリトープをメインに考えます.
- (1)
- $\mathbb Z^d$ の元 (つまり, 座標の各成分が整数である点) を格子点と呼び, 格子点を頂点とするポリトープを格子ポリトープ (lattice polytope) と呼ぶ.
- (2)
- $\mathbb Q^d$ の元 (つまり, 座標の各成分が有理数である点) を有理点と呼び,
有理点を頂点とするポリトープを有理ポリトープ (rational polytope) と呼ぶ.
ここまでは, 一般的な定義です.
これらを用いて, 格子ポリトープの「ミニチュア」を, 次のように定義します (現時点で私の知る限りどの文献にも載っていないオリジナルの概念です).
「平均大のミニチュア」「標準大のミニチュア」を定義するために, 面積, 体積の一般化である「超体積」の概念も用います (定義は割愛しますが, 本稿では $1$ 辺の長さが $a$ の $d$ 次元超立方体の超体積が $a^d$ であることを押さえておけば大丈夫です).
$P \subset \mathbb R^d$ を格子ポリトープとする.
- (1)
- ポリトープ $M \subset \mathbb R^d$ が
- (i)
- $M \subset P$
- (ii)
- $M$ は $P$ と相似である
- (iii)
- $M$ は有理ポリトープである
を満たすとき, $M$ を $P$ のミニチュア (miniature) と呼ぶ.
さらに, $M$ を何倍かに拡大したものが $P$ と平行移動で移り合うとき, $M$ は水平 (horizontal) であるという.
- (2)
- $n$ を正の整数とする.
$M$ が $P$ のミニチュアであり,
| $M$ の各頂点の座標の各成分が分母を $n$ とする有理数として表される |
とき, $M$ を解像度 $n$ の $P$ のミニチュア (miniature of $P$ with resolution $n$) と呼ぶ.
- (3)
- 解像度 $n$ の $P$ のミニチュア全体のなす集合を $\mathcal M_n(P)$ で表す.
そのようなミニチュア $M$ の超体積の平均値の極限値
| $\lim\limits_{n \to \infty}\dfrac{\sum_{M \in \mathcal M_n(P)}\mathrm{vol}(M)}{\#\mathcal M_n(P)}$ ($\mu_{\mathrm{av}}(P)$ で表す) |
が存在するとき, $P$ は $\mu_{\mathrm{av}}$ 可測 ($\mu_{\mathrm{av}}$-measurable) であるといい, $\mu_{\mathrm{av}}(P)$ と同じ超体積をもつような $P$ と相似なポリトープを $P$ の平均大のミニチュア (average-sized miniature of $P$) と呼ぶ.
- (4)
- 解像度 $n$ の $P$ の水平なミニチュア全体のなす集合を $\mathcal H_n(P)$ で表す.
そのようなミニチュア $M$ の超体積の平均値の極限値
| $\lim\limits_{n \to \infty}\dfrac{\sum_{M \in \mathcal H_n(P)}\mathrm{vol}(M)}{\#\mathcal H_n(P)}$ ($\mu_{\mathrm{nl}}(P)$ で表す) |
が存在するとき, $P$ は $\mu_{\mathrm{nl}}$ 可測 ($\mu_{\mathrm{nl}}$-measurable) であるといい, $\mu_{\mathrm{nl}}(P)$ と同じ超体積をもつような $P$ と相似なポリトープを $P$ の標準大のミニチュア (normal-sized miniature of $P$) と呼ぶ.
これらの概念を用いると, 命題 1 の中で考えた問題は, 次のように一般化できます.
与えられた格子ポリトープ $P \subset \mathbb R^d$ に対する $P$ の平均大のミニチュア, $P$ の標準大のミニチュアの超体積の比はそれぞれいくらか.
本稿の第 $1$ の主定理は, 超立方体の標準大のミニチュアに関する結果です.
$H$ を $d$ 次元超立方体 $[0,1]^d$ とする.
- (1)
- $H$ に対する $H$ の標準大のミニチュアの超体積の比は
| $\dfrac{1}{\dbinom{2d+1}{d}} = \dfrac{d!(d+1)!}{(2d+1)!}$ |
である.
- (2)
- $d \to \infty$ のときの $H$ に対する $H$ の標準大のミニチュアの辺の長さの比の極限値は $\dfrac{1}{4}$ である.
$\dbinom{2d+1}{d}$ は相異なる $2d+1$ 個のものから $d$ 個取る組合せの総数 (二項係数) を表す.
第 $2$ の主定理は, 限定的ですが, 正方形の平均大のミニチュアに関する結果です.
格子正方形 $[0,1]^2 \subset \mathbb R^2$ に対する $[0,1]^2$ の平均大のミニチュアの面積の比は $\dfrac{2}{15}$ である.
これらの定理の証明は, それぞれ §3, 4 で述べます.
- ※4:
- 筆者が河口湖の湖畔を散歩中にこの定理の問題を思い付いたので ($2024$ 年 $2$ 月), 個人的にこの定理を河口湖の定理と呼んでいます.
本節では, 定理 1 を証明します.
【定理 1 (1) の証明】
解像度 $n$ の $H$ の水平なミニチュアのうち, $1$ 辺の長さが $\dfrac{k}{n}$ であるものは $(n-k+1)^d$ 個あります.
これらのミニチュアの超体積の総和 (延べ超体積) は
\[\sum_{k = 1}^n(n-k+1)^d\left(\frac{k}{n}\right)^d\]
であり, これらのミニチュアの総数は
\[\sum_{k = 1}^n(n-k+1)^d = \sum_{k = 1}^nk^d\]
であるので, $H$ の超体積が $1$ であることに注意すると, 求める比は
| $\lim\limits_{d \to \infty}\dfrac{\displaystyle\sum_{k = 1}^n(n-k+1)^dk^d}{\displaystyle n^d\sum_{k = 1}^nk^d}$ (この値を $L$ とおきます) |
に等しいことがわかります.
分母, 分子はともに $n$ の $2d+1$ 次式であるので, それぞれの最高次の係数に注目すると,
\[ L = \frac{\displaystyle\sum_{k = 0}^d\frac{(-1)^k}{d+1+k}\binom{d}{k}}{\dfrac{1}{d+1}} = (d+1)\sum_{k = 0}^d\dfrac{(-1)^k}{d+1+k}\binom{d}{k}\]
であることがわかります.
ここで,
| $x^d(1+x)^d = \displaystyle\sum_{k = 0}^d\binom{d}{k}x^{d+k}$ |
の両辺を $-1$ から $0$ まで積分して得られる等式
\[\int_{-1}^0x^d(1+x)^d\,dx = \sum_{k = 0}^d\binom{d}{k}\int_{-1}^0x^{d+k}\,dx\]
において, $B(x,y)$ をベータ関数として
\[\begin{aligned}
\int_{-1}^0x^d(1+x)^d\,dx &= \int_1^0(-t)^d(1-t)^d(-1)\,dt \\
&= (-1)^d\int_0^1t^d(1-t)^d\,dt \\
&= (-1)^dB(d+1,d+1) \\
&= (-1)^d\frac{d!d!}{(2d+1)!} \\
&= \frac{(-1)^d}{\displaystyle (d+1)\binom{2d+1}{d}}, \\
\sum_{k = 0}^d\binom{d}{k}\int_{-1}^0x^{d+k}\,dx &= \sum_{k = 0}^d\binom{d}{k}\left[\frac{x^{d+1+k}}{d+1+k}\right] _{-1}^0 \\
&= (-1)^d\sum_{k = 0}^d\frac{(-1)^k}{d+1+k}\binom{d}{k}
\end{aligned}\]
であるので,
\[ L = \frac{1}{\dbinom{2d+1}{d}}\]
が得られます.
■
【定理 1 (2) の証明】
\[\binom{2d+1}{d} = \frac{2d+1}{d+1}\binom{2d}{d}, \quad \lim\limits_{d \to \infty}\sqrt[d]{\frac{2d+1}{d+1}} = 1\]
であるので, 公式
\[\lim\limits_{d \to \infty}\sqrt[d]{\binom{2d}{d}} = 4\]
により,
\[\lim\limits_{d \to \infty}\sqrt[d]{\binom{2d+1}{d}} = 4\]
です.
ゆえに, $H$ の $1$ 辺の長さが $1$ であることに注意すると, 求める比の極限値は
\[\lim_{d \to \infty}\sqrt[d]{\frac{1}{\dbinom{2d+1}{d}}} = \lim_{d \to \infty}\frac{1}{\sqrt[d]{\dbinom{2d+1}{d}}} = \frac{1}{4}\]
であることがわかります.
■
命題 1 の極限値 $\dfrac{1}{10}$ は二項係数 $\dbinom{5}{2} = 10$ から来ていること (逆数をとったものである) ことがわかりました.
本節では, 次の補題を用いて, 定理 2 を証明します.
任意の正の整数 $n$ に対して,
- (1)
- $\begin{aligned}
\displaystyle\sum_{k = 1}^nk(n+1-k)^2 &= \sum_{k = 1}^nk^2(n+1-k) \\
&= \frac{1}{12}n(n+1)^2(n+2)
\end{aligned}$
- (2)
- $\begin{aligned}
\displaystyle\sum_{k = 1}^nk^2(n+1-k)^3 &= \sum_{k = 1}^nk^3(n+1-k)^2 \\
&= \frac{1}{60}n(n+1)^2(n+2)(n^2+2n+2)
\end{aligned}$
が成り立つ.
【定理 2 の証明】
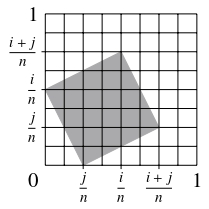
解像度 $n$ の $H = [0,1]^2$ のミニチュアの面積の平均値を $p_n$ とおきます.
各
\[ (i,j) \in \{ (i,j) \in \mathbb Z^2 \mid 1 \leqq i \leqq n,\ 0 \leqq j \leqq n-i\}\]
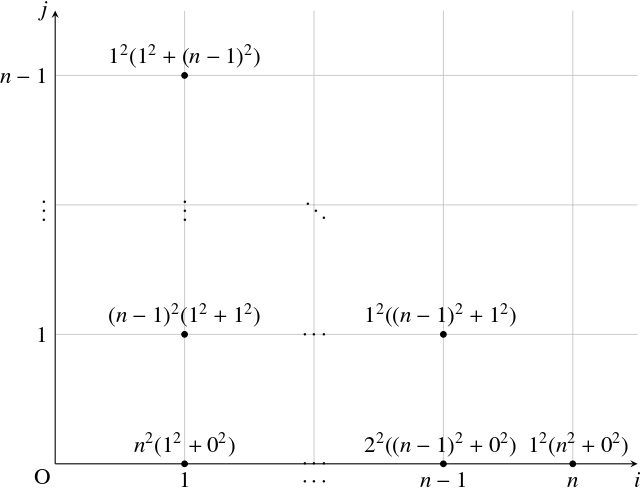
に対して, $[0,1]^2$ 上にベクトル $\left(\dfrac{i}{n},\dfrac{j}{n}\right),$ $\left(\dfrac{j}{n},-\dfrac{i}{n}\right)$ で張られる解像度 $n$ の $H$ のミニチュアを配置する方法は $(n+1-i-j)^2$ 通りあり, その面積は $\dfrac{(\sqrt{i^2+j^2})^2}{n^2} = \dfrac{i^2+j^2}{n^2}$ です.
よって,
補題 (1) により, 解像度 $n$ の $H$ のミニチュアの総数は
\[\begin{aligned}
\sum_{i = 1}^n\sum_{j = 0}^{n-i}(n+1-i-j)^2 &= \sum_{k = 1}^n(n+1-k)k^2 \\
&= \frac{1}{12}n(n+1)^2(n+2)
\end{aligned}\]
です.
ここで, 第 $1$ の等号は, 次の図の
左上から右下への対角線方向へ和をとり直すことによりわかります.
また,
補題 (1), (2) により, 解像度 $n$ の $H$ のミニチュアの延べ面積は
\[\begin{aligned}
&\sum_{i = 1}^n\sum_{j = 0}^{n-i}(n+1-i-j)^2\frac{i^2+j^2}{n^2} \\
&= \frac{1}{n^2}\sum_{k = 1}^nk^2\left(\sum_{i = 1}^{n+1-k}i^2+\sum_{j = 0}^{n-k}j^2\right) \\
&= \frac{1}{n^2}\sum_{k = 1}^nk^2\left( 0^2+2\sum_{i = 1}^{n-k}i^2+(n+1-k)^2\right) \\
&= \frac{1}{n^2}\sum_{k = 1}^nk^2\left(\frac{1}{3}(n-k)(n-k+1)(2n-2k+1)+(n+1-k)^2\right) \\
&= \frac{1}{n^2}\left(\frac{1}{3}\sum_{k = 1}^nk^2(n-k)(n-k+1)(2n-2k+1)\right. \\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \left. +\sum_{k = 1}^nk^2(n+1-k)^2\right) \\
&= \frac{1}{n^2}\left(\frac{1}{3}\sum_{k = 1}^n(n+1-k)^2(k-1)k(2k-1)\right. \\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \left. +\sum_{k = 1}^nk^2(n+1-k)^2\right) \\
&= \frac{1}{3n^2}\sum_{k = 1}^nk((k-1)(2k-1)+3k)(n+1-k)^2 \\
&= \frac{1}{3n^2}\sum_{k = 1}^nk(2k^2+1)(n+1-k)^2 \\
&= \frac{1}{n^2}\left(\frac{2}{3}\sum_{k = 1}^nk^3(n+1-k)^2+\frac{1}{3}\sum_{k = 1}^nk(n+1-k)^2\right) \\
&= \frac{1}{n^2}\left(\frac{2}{3}\cdot\frac{1}{60}n(n+1)^2(n+2)(n^2+2n+2)\right. \\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \left. +\frac{1}{3}\cdot\frac{1}{12}n(n+1)^2(n+2)\right) \\
&= \frac{1}{180n}(n+1)^2(n+2)(2(n^2+2n+2)+5) \\
&= \frac{1}{180n}(n+1)^2(n+2)(2n^2+4n+9)
\end{aligned}\]
です.
ここで, 第 $1$ の等号は, 次の図の
左上から右下への対角線方向へ和をとり直すことによりわかります.
ゆえに,
\[\begin{aligned}
p_n &= \frac{\displaystyle\sum_{i = 1}^n\sum_{j = 0}^{n-i}(n+1-i-j)^2\frac{i^2+j^2}{n^2}}{\displaystyle\sum_{i = 1}^n\sum_{j = 0}^{n-i}(n+1-i-j)^2} \\
&= \frac{\dfrac{1}{180n}(n+1)^2(n+2)(2n^2+4n+9)}{\dfrac{1}{12}n(n+1)^2(n+2)} \\
&= \frac{2n^2+4n+9}{15n^2} \\
&\to \frac{2}{15} \quad (n \to \infty )
\end{aligned}\]
が得られます.
■
正方形 $[0,1]^2$ に対して, 任意の方向のミニチュアを考慮に入れると, それらの「平均的な面積」は $\dfrac{2}{15} = 0.1\dot 3$ となり, 命題 1 の極限値 $\dfrac{1}{10} = 0.1$ より少し大きくなることがわかりました.
次の問題を解決することが当面の課題です.
どのような格子ポリトープ $P \subset \mathbb R^d$ が $\mu_{\mathrm{av}}$ 可測 (resp. $\mu_{\mathrm{nl}}$ 可測) であるか.
また, $P$ を動かしたとき, $P$ の超体積に対する $\mu_{\mathrm{av}}(P)$ (resp. $\mu_{\mathrm{nl}}(P)$) の比の上限, 下限はいくらか.
特に, $d \geqq 3$ のとき, $d$ 次元超立方体 $H$ に対する $H$ の平均大のミニチュアの体積比はいくらか.
格子ポリトープ $P \subset \mathbb R^d$ に対する $P$ の平均大 (標準大) のミニチュアの超体積の比は, $P$ をそれと相似な格子ポリトープに取り替えても同じ値になるか.
格子ポリトープ $P_1,$ $P_2 \subset \mathbb R^d$ が $\mu_{\mathrm{av}}$ 可測 (resp. $\mu_{\mathrm{nl}}$ 可測) で共通部分が超平面上にあるとき, $P_1\cup P_2$ も $\mu_{\mathrm{av}}$ 可測 (resp. $\mu_{\mathrm{nl}}$ 可測) であり,
| $\mu_{\mathrm{av}}(P_1\cup P_2) = \mu_{\mathrm{av}}(P_1)+\mu_{\mathrm{av}}(P_2)$ |
| (resp. $\mu_{\mathrm{nl}}(P_1\cup P_2) = \mu_{\mathrm{nl}}(P_1)+\mu_{\mathrm{nl}}(P_2)$) |
は成り立つか.
本稿の内容については, これから先の研究を模索している段階ですが, 類似の研究結果, より進んだ研究結果をご存知の方がいらっしゃれば, お知らせいただければ幸いです.
長文にもかかわらず最後まで読んでいただき, ありがとうございました.
問題 3 について, 次の定理が証明できました.
格子ポリトープ $P,$ $P' \subset \mathbb R^d$ に対して, $P,$ $P'$ が相似で $\mu_{\mathrm{av}}$ 可測 (resp. $\mu_{\mathrm{nl}}$ 可測) ならば,
| $\dfrac{\mu_{\mathrm{av}}(P)}{\mathrm{vol}(P)} = \dfrac{\mu_{\mathrm{av}}(P')}{\mathrm{vol}(P')}$ |
| (resp. $\dfrac{\mu_{\mathrm{nl}}(P)}{\mathrm{vol}(P)} = \dfrac{\mu_{\mathrm{nl}}(P')}{\mathrm{vol}(P')}$) |
が成り立つ.
格子ポリトープ $P \subset \mathbb R^d,$ ベクトル $a \in \mathbb R^d,$ 整数 $c > 0$ に対して, ポリトープ $\{ x+a \mid x \in P\},$ $\{ cx \mid x \in P\}$ をそれぞれ $P+a,$ $cP$ で表すことにして, 次の概念, 補題を使います.
$P \subset \mathbb R^d$ を格子ポリトープとする.
格子ポリトープであるような $P$ の水平なミニチュアのうち超体積が最小のものを $P$ の基本ミニチュア (fundamental miniature) と呼ぶ.
$P$ が $P$ の唯一の基本ミニチュアであるとき $P$ は既約 (irreducible) である, そうでないとき $P$ は可約 (reducible) であるという.
$P \subset \mathbb R^d$ を $\mu_{\mathrm{av}}$ 可測 (resp. $\mu_{\mathrm{nl}}$ 可測) な格子ポリトープとし, $a \in \mathbb Z^d$ とする.
このとき, $P+a$ も $\mu_{\mathrm{av}}$ 可測 (resp. $\mu_{\mathrm{nl}}$ 可測) であり,
| $\mu_{\mathrm{av}}(P+a) = \mu_{\mathrm{av}}(P)$ |
| (resp. $\mu_{\mathrm{nl}}(P+a) = \mu_{\mathrm{nl}}(P)$) |
が成り立つ.
【補題 1 の証明】
各整数 $n > 0$ に対して, $P\cap (\mathbb Z[n^{-1}])^d$ の各点は平行移動 $x \mapsto x+a$ により $(P+a)\cap (\mathbb Z[n^{-1}])^d$ の点にうつされるので,
\[\begin{aligned}
\mathcal M_n(a+P) &= \{ a+M \mid M \in \mathcal M_n(P)\}, \\
\mathcal H_n(a+P) &= \{ a+M \mid M \in \mathcal H_n(P)\}
\end{aligned}\]
が成り立ち, よって求める主張が成り立ちます.
■
$P \subset \mathbb R^d$ を $\mu_{\mathrm{av}}$ 可測 (resp. $\mu_{\mathrm{nl}}$ 可測) な格子ポリトープとし, $c \in \mathbb Z$ $(c > 0)$ とする.
このとき, $cP$ も $\mu_{\mathrm{av}}$ 可測 (resp. $\mu_{\mathrm{nl}}$ 可測) であり,
| $\mu_{\mathrm{av}}(cP) = c\,\mu_{\mathrm{av}}(P)$ |
| (resp. $\mu_{\mathrm{nl}}(cP) = c\,\mu_{\mathrm{nl}}(P)$) |
が成り立つ.
【補題 2 の証明】
各整数 $n > 0$ に対して, $P\cap (\mathbb Z[(cn)^{-1}])^d$ の各点はスケール変換 $x \mapsto cx$ により $cP\cap (\mathbb Z[n^{-1}])^d$ の点にうつされるので,
\[\begin{aligned}
\mathcal M_n(cP) &= \{ cM \mid M \in \mathcal M_{cn}(P)\}, \\
\mathcal H_n(cP) &= \{ cM \mid M \in \mathcal H_{cn}(P)\}
\end{aligned}\]
が成り立ち, よって求める主張が成り立ちます.
■
$P,$ $P' \subset \mathbb R^d$ を互いに相似な $\mu_{\mathrm{av}}$ 可測 (resp. $\mu_{\mathrm{nl}}$ 可測) で既約な格子ポリトープとする.
このとき,
| $\dfrac{\mu_{\mathrm{av}}(P)}{\mathrm{vol}(P)} = \dfrac{\mu_{\mathrm{av}}(P')}{\mathrm{vol}(P')}$ |
| (resp. $\dfrac{\mu_{\mathrm{nl}}(P)}{\mathrm{vol}(P)} = \dfrac{\mu_{\mathrm{nl}}(P')}{\mathrm{vol}(P')}$) |
が成り立つ.
$P,$ $P' \subset \mathbb R^d$ を格子ポリトープとする.
$P$ が既約で, $P \sim P'$ であり, $P$ が同型写像 $\tau :\mathbb R^d\to\mathbb R^d$ で $P'$ にうつされるとする.
- (1)
- このとき,
\[\begin{aligned}
\mathcal M_n(P') &\supset \{\tau (M) \mid M \in \mathcal M_n(P)\}, \\
\mathcal H_n(P') &\supset \{\tau (M) \mid M \in \mathcal H_n(P)\}
\end{aligned}\]
が成り立つ.
- (2)
- さらに, $P'$ が既約ならば,
\[\begin{aligned}
\mathcal M_n(P') &= \{\tau (M) \mid M \in \mathcal M_n(P)\}, \\
\mathcal H_n(P') &= \{\tau (M) \mid M \in \mathcal H_n(P)\}
\end{aligned}\]
が成り立つ.
【部分補題 の証明】
- (1)
- $\{ 0,v_1,\dots,v_d\} \subset \mathbb Z^d$ を $P$ の頂点全体からなる集合とします.
各整数 $n > 0$ に対して, $P\cap (\mathbb Z[n^{-1}])^d$ の各点 $\sum a_iv_i$ $((a_i) \in (\mathbb Z[n^{-1}])^d)$ は $\tau$ により $\tau (P)\cap (\mathbb Z[n^{-1}])^d$ の点 $\sum a_i\tau (v_i)$ にうつされるので, 求める包含関係が成り立ちます.
- (2)
- 対偶を示します.
$M' \in \mathcal M_n(P')\setminus\{\tau (M) \mid M \in \mathcal M_n(P)\}$ とします.
$H'$ を $M' \subset H'$ を満たし, 格子ポリトープであるような $P'$ の水平なミニチュア $H'$ のうち超体積が最小のものとします.
このとき, $P$ が既約であることから $\tau ^{-1}(H') \neq P$ よって $H' \neq P'$ が成り立ち, これは $P'$ が可約であることを意味します. ■
これで, 定理 3 を証明する準備ができました.
【定理 3 の証明】
$P_0,$ $P'_0$ をそれぞれ $P,$ $P'$ の基本ミニチュアとします.
このとき, ベクトル $a,$ $a' \in \mathbb Z^d,$ 整数 $c,$ $c' > 0,$ 同型写像 $\tau :\mathbb R^d\to\mathbb R^d$ で
\[ P = c(P_0-a)+a,\ P' = c'(P'_0-a')+a',\ P'_0-a = \tau (P_0-a)\]
を満たし, $P_0-a,$ $P'_0-a'$ が原点を頂点にもつようなものが存在します.
よって, 補題 1~3 を合わせることにより,
| $\displaystyle\frac{\mu_{\mathrm{av}}(P)}{\mathrm{vol}(P)} = \frac{c\,\mu_{\mathrm{av}}(P_0)}{c\,\mathrm{vol}(P_0)} = \frac{c'\,\mu_{\mathrm{av}}(P'_0)}{c'\,\mathrm{vol}(P'_0)} = \frac{\mu_{\mathrm{av}}(P')}{\mathrm{vol}(P')}$ |
| (resp. $\displaystyle\frac{\mu_{\mathrm{nl}}(P)}{\mathrm{vol}(P)} = \frac{c\,\mu_{\mathrm{nl}}(P_0)}{c\,\mathrm{vol}(P_0)} = \frac{c'\,\mu_{\mathrm{nl}}(P'_0)}{c'\,\mathrm{vol}(P'_0)} = \frac{\mu_{\mathrm{nl}}(P')}{\mathrm{vol}(P')}$) |
が得られます.
■
定理 3 により, 面積が $A$ である任意の格子正方形 $P \subset \mathbb R^2$ に対して
\[\mu _\mathrm{av}(P) = \frac{2}{15}A\]
であることが分かります.
問題 2 について, 部分的ではありますが, 次の定理が証明できました.
「単体」とは, 平面における三角形, 空間における四面体を一般化した概念です.
任意の格子単体 $P \subset \mathbb R^d$ に対して, $P$ は $\mu_{\mathrm{nl}}$ 可測であり,
\[\mu_{\mathrm{nl}}(P) = \binom{2d+1}{d}^{-1}\mathrm{vol}(P)\]
が成り立つ.
証明には, 次の概念 (一般的な概念) を使います.
数列 $\{ S_d(n)\}$ を
\[ S_0(n) = 1, \quad S_d(n) = \sum_{i = 1}^nS_{d-1}(i) \quad (d > 0)\]
で定め, $S_d(n)$ を $n$ 番目の $d$ 次元単体数 ($d$-dimensional simplex number) と呼ぶ.
よく知られているように, 次の公式が成り立ちます.
任意の整数 $n > 0$ に対して,
\[ S_d(n) = \binom{n+d-1}{d}\]
が成り立つ.
この公式を使って, 次の命題を示します.
任意の整数 $r \geqq 0,$ $n > 0$ に対して,
\[\sum_{i = 1}^n i^rS_d(i) = \frac{n^{d+r+1}}{d!(d+r+1)}+O(n^{d+r})\]
が成り立つ.
ここで, $O$ はランダウの記号を表す.※5
- ※5:
- $n$ 次多項式 $f(x)$ に対しては, $f(x) = a_nx^n+O(x^{n-1})$ は $f(x)$ の $n$ 次の項が $a_nx^n$ であることを表します.
【命題 3 の証明】
\[ S_d(i) = \frac{1}{d!}i^d+O(i^{d-1}), \quad \sum_{i = 1}^n i^k = \frac{1}{k+1}n^{k+1}+O(n^k)\]
$(k = d+r)$ が成り立つことから従います.
■
【定理 4 の証明】
$1 \leqq i \leqq n$ なる整数 $i$ に対して $P$ の水平なミニチュアで相似比が $i/n$ であるものの個数は $S_d(n+1-i)$ であるから, 二項定理により
\[\begin{aligned}
&\frac{\sum_{M \in \mathcal H_n(P)}\mathrm{vol}(M)}{\#\mathcal H_n(P)} \\
&= \left.\left(\sum_{i = 1}^n S_d(n+1-i)\cdot\left(\frac{i}{n}\right) ^d\mathrm{vol}(P)\right)\middle/\sum_{i = 1}^n S_d(n+1-i)\right. \\
&= \left.\mathrm{vol}(P)\cdot\left(\sum_{i = 1}^n (n+1-i)^dS_d(i)\right)\middle/ n^d\sum_{i = 1}^n S_d(i)\right. \\
&= \left.\mathrm{vol}(P)\cdot\left(\sum_{i = 1}^n S_d(i)\sum_{r = 0}^d\binom{d}{r}(n+1)^{d-r}(-i)^r\right)\middle/ n^dS_{d+1}(n)\right. \\
&= \left.\mathrm{vol}(P)\cdot\left(\sum_{r = 0}^d (-1)^r\binom{d}{r}(n+1)^{d-r}\sum_{i = 1}^n i^rS_d(i)\right)\middle/ n^dS_{d+1}(n)\right.
\end{aligned}\]
が成り立ちます.
さらに,
\[\begin{aligned}
(n+1)^{d-r}\sum_{i = 1}^n i^rS_d(i) &= \frac{1}{d!(d+r+1)}n^{2d+1}+O(n^{2d}), \\
n^dS_{d+1}(n) &= \frac{1}{(d+1)!}n^{2d+1}+O(n^{2d})
\end{aligned}\]
であるから,
定理 1 (1) の証明の中で示した等式
\[ (d+1)\sum_{k = 0}^d\dfrac{(-1)^k}{d+1+k}\binom{d}{k} = \frac{1}{\dbinom{2d+1}{d}}\]
により
\[\begin{aligned}
&\frac{\sum_{M \in \mathcal H_n(P)}\mathrm{vol}(M)}{\#\mathcal H_n(P)} \\
&\to \left.\mathrm{vol}(P)\cdot\left(\sum_{r = 0}^d(-1)^r\binom{d}{r}\frac{1}{d!(d+r+1)}\right)\middle/\dfrac{1}{(d+1)!}\right. \\
&= \mathrm{vol}(P)\cdot (d+1)\sum_{r = 0}^d\frac{(-1)^r}{d+r+1}\binom{d}{r} \\
&= \binom{2d+1}{d}^{-1}\mathrm{vol}(P) \quad (n \to \infty )
\end{aligned}\]
が成り立ちます.
■
- 2024/12/18
- 公開
- 誤植の修正, リンクの修正
- 図の追加
- 問題 3 の加筆
- 2024/12/19
- 一部加筆, 強調の追加
- 2024/12/21
- リンクの追加, 一部改訂
- 2024/12/24
- 補題 2
- 2024/12/25
- 定義, 補題 1, 3
- 2024/12/26
- 水平の定義の導入, 定理 3 の証明
- 2024/12/30
- 問題 4
- 2025/01/01
- 補題 3 の証明の改訂, 部分補題
- 2025/01/02
- 定理 3, 補題 1~3 の加筆
- 2025/01/04
- 定理 4, 誤植の修正
お気づきの点などがありましたら, 以下の連絡先までお願いします.
- 氏 名
- 廣津 孝 (ひろつ たかし)
- (理学博士)
- メール