面積 (文系・理系共通)
面積
定理《$2$ つの関数のグラフと $x = a,$ $x = b$ が囲む図形の面積》
$a,$ $b$ を $a < b$ なる実数とし, $f(x),$ $g(x)$ を多項式とする.
曲線 $y = f(x),$ $y = g(x)$ と直線 $x = a,$ $x = b$ で囲まれた図形の面積 $S$ は,
\[ S = \int_a^b|f(x)-g(x)|\,dx\]
である.
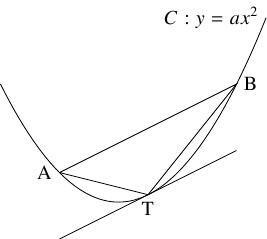
問題《アルキメデスの定理》
$a$ を正の数とし, 放物線 $C:y = ax^2$ 上に相異なる $2$ 点 $\mathrm A(\alpha,a\alpha ^2),$ $\mathrm B(\beta,a\beta ^2)$ をとる.
さらに, $C$ 上の点 $\mathrm T(t,at^2)$ を, $C$ の $\mathrm T$ における接線と直線 $\mathrm{AB}$ の傾きが一致するようにとる.
- (1)
- $\displaystyle\int_\alpha ^\beta (x-\alpha )(x-\beta )\,dx = -\frac{(\beta -\alpha )^3}{6}$ を示せ.
- (2)
- $\alpha,$ $\beta$ を用いて $t$ を表せ.
- (3)
- $C$ と直線 $\mathrm{AB}$ で囲まれた図形の面積 $S$ について, $S = \dfrac{4}{3}\triangle\mathrm{ABT}$ が成り立つことを示せ.
解答例
- (1)
- \[\begin{aligned} (x-\alpha )(x-\beta ) &= (x-\alpha )\{ (x-\alpha )-(\beta -\alpha )\} \\ &= (x-\alpha )^2-(\beta -\alpha )(x-\alpha ) \end{aligned}\] から, \[\begin{aligned} \int_\alpha ^\beta (x-\alpha )(x-\beta )\,dx &= \int_\alpha ^\beta\{ (x-\alpha )^2-(\beta -\alpha )(x-\alpha )\}\,dx \\ &= \left[\frac{(x-\alpha )^3}{3}-(\beta -\alpha )\frac{(x-\alpha )^2}{2}\right] _\alpha ^\beta \\ &= -\frac{(\beta -\alpha )^3}{6} \quad \cdots [1] \end{aligned}\] が成り立つ.
- (2)
- $y = ax^2$ の導関数は $y' = 2ax$ であるから, $C$ の点 $\mathrm T$ における接線の傾きについて \[ 2at = \frac{a\beta ^2-a\alpha ^2}{\beta -\alpha} = a(\alpha +\beta )\] が成り立つ. よって, \[ t = \frac{\alpha +\beta}{2}\] である.
- (3)
- 直線 $\mathrm{AB}$ の方程式は
\[ y-a\alpha ^2 = \frac{a\beta ^2-a\alpha ^2}{\beta -\alpha}(x-\alpha )\]
つまり
\[ y = a(\alpha +\beta )x-a\alpha\beta\]
であるから, $[1]$ により
\[\begin{aligned}
S &= \int_\alpha ^\beta \{ a(\alpha +\beta )x-a\alpha\beta -ax^2\}\,dx \\
&= -a\int_\alpha^\beta (x-\alpha )(x-\beta )\,dx \\
&= \frac{a}{6}(\beta -\alpha )^3
\end{aligned}\]
である.
また, 点 $\mathrm A,$ $\mathrm B,$ $\mathrm T$ を $x$ 軸方向に $-\dfrac{\alpha +\beta}{2},$ $y$ 軸方向に $-a\dfrac{(\alpha +\beta )^2}{4}$ だけ平行移動した点は $\mathrm A'\left(\dfrac{\alpha -\beta}{2},a\dfrac{4\alpha ^2-(\alpha +\beta )^2}{4}\right),$ $\mathrm B'\left(\dfrac{\beta -\alpha}{2},a\dfrac{4\beta ^2-(\alpha +\beta )^2}{4}\right),$ $\mathrm O(0,0)$ であるから, \[\begin{aligned} &\triangle\mathrm{ABT} = \triangle\mathrm{OA}'\mathrm B' \\ &= \frac{1}{2}\left|\frac{\alpha -\beta}{2}\cdot a\frac{4\beta ^2-(\alpha +\beta )^2}{4}-a\frac{4\alpha ^2-(\alpha +\beta )^2}{4}\cdot\frac{\beta -\alpha}{2}\right| \\ &= \frac{1}{2}\cdot\frac{a}{4}\cdot\frac{\beta -\alpha}{2}|2(\alpha +\beta )^2-4\alpha ^2-4\beta ^2| \\ &= \frac{a}{8}(\beta -\alpha )^3 \end{aligned}\] である. ゆえに, \[ S = \frac{4}{3}\cdot\frac{a}{8}(\beta -\alpha )^3 = \frac{4}{3}\triangle\mathrm{ABT}\] が成り立つ.
参考
(3) の結果は「アルキメデスの定理」(Archimedes' theorem) として有名である.
アルキメデスは紀元前に, $\triangle\mathrm{ABT}$ に次々と小さな三角形の面積を加えていく方法でこれを示した.
問題《放物線と接線が囲む図形の面積》
$2$ 次関数 $f(x) = ax^2+bx+c,$ $g(x) = ax^2+b'x+c'$ ($a,$ $b,$ $c,$ $b',$ $c'$: 実数, $b \neq b'$) について, 次のことを示せ.
- (1)
- 放物線 $y = f(x)$ とその点 $(\alpha,f(\alpha))$ における接線, 直線 $x = p$ が囲む図形の面積 $S$ は \[ S = \frac{|a|}{3}|p-\alpha |^3\] である.
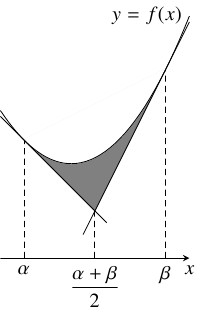
- (2A)
- 放物線 $y = f(x)$ とその点 $(\alpha,f(\alpha)),$ $(\beta,f(\beta ))$ $(\alpha < \beta )$ における接線が囲む図形の面積 $S$ は \[ S = \frac{|a|}{12}(\beta -\alpha )^3\] である.
- (2B)
- $2$ つの放物線 $C:y = f(x),$ $C':y = g(x)$ が直線 $l$ とそれぞれ点 $(\alpha,f(\alpha)),$ $(\beta,g(\beta ))$ $(\alpha < \beta )$ で接するとき, $C,$ $C',$ $l$ が囲む図形の面積 $S$ は \[ S = \frac{|a|}{12}(\beta -\alpha )^3\] である.
解答例
- (1)
- $f'(x) = 2ax+b$ であるから, 放物線 $y = f(x)$ の点 $(\alpha,f(\alpha ))$ における接線の方程式は, \[ y-(a\alpha ^2+b\alpha +c) = (2a\alpha +b)(x-\alpha )\] つまり \[ y = (2a\alpha +b)x-a\alpha ^2+c\] である. この右辺を $g(x)$ とおくと, \[\begin{aligned} &f(x)-g(x) \\ &= (ax^2+bx+c)-\{ (2a\alpha +b)x-a\alpha ^2+c\} \\ &= ax^2-2a\alpha x+a\alpha ^2 = a(x-\alpha )^2 \end{aligned}\] となるから, \[\begin{aligned} S &= \left|\int_\alpha ^p|f(x)-g(x)|\,dx\right| = |a|\left|\int_\alpha ^p(x-\alpha )^2\,dx\right| \\ &= |a|\left|\left[\frac{(x-\alpha )^3}{3}\right] _\alpha ^p\right| = |a|\left|\frac{(p-\alpha )^3}{3}\right| = \frac{|a|}{3}|p-\alpha |^3 \end{aligned}\] が成り立つ.
- (2A)
- 放物線 $y = f(x)$ の点 $(\beta,f(\beta ))$ における接線の方程式は,
\[ y = (2a\beta +b)x-a\beta ^2+c\]
である.
よって, $2$ 本の接線の交点の $x$ 座標は,
\[ (2a\alpha +b)x-a\alpha ^2+c = (2a\beta +b)x-a\beta ^2+c\]
の解であるから, $a \neq 0,$ $\alpha \neq \beta$ に注意すると,
\[ x = \frac{a(\beta ^2-\alpha ^2)}{2a(\beta -\alpha )} = \frac{\alpha +\beta}{2}\]
である.
$y = f(x)$ と $2$ 本の接線が囲む図形の面積は, 直線 $x = \dfrac{\alpha +\beta}{2}$ で $2$ つに分けて考えると, (1) により
\[\begin{aligned}
S &= \frac{|a|}{3}\left(\frac{\alpha +\beta}{2}-\alpha\right) ^3+\frac{|a|}{3}\left(\beta -\frac{\alpha +\beta}{2}\right) ^3 \\
&= 2\cdot\frac{|a|}{3}\left(\frac{\beta -\alpha}{2}\right) ^3 = \frac{|a|}{12}(\beta -\alpha )^3
\end{aligned}\]
であることがわかる.
- (2B)
- (1) で求めたように放物線 $C:y = f(x)$ の点 $(\alpha,f(\alpha ))$ における接線, $C':y = g(x)$ の点 $(\beta,g(\beta ))$ における接線の方程式はそれぞれ \[\begin{aligned} y &= (2a\alpha +b)x-a\alpha ^2+c, \\ y &= (2a\beta +b')x-a\beta ^2+c' \\ \end{aligned}\] であり, これらが一致するから \[ 2a\alpha +b = 2a\beta +b', \quad -a\alpha ^2+c = -a\beta ^2+c'\] つまり \[ b-b' = 2a(\beta -\alpha ), \quad c'-c = a(\beta ^2-\alpha ^2)\] が成り立つ. また, $C,$ $C'$ の共有点の $x$ 座標は \[ ax^2+bx+c = ax^2+b'x+c'\] の解であるから, その値は \[ x = \frac{c'-c}{b-b'} = \frac{a(\beta ^2-\alpha ^2)}{2a(\beta -\alpha )} = \frac{\alpha+\beta}{2}\] である. よって, $C,$ $C',$ $l$ が囲む図形の面積は, (1) により, \[\begin{aligned} S &= \frac{|a|}{3}\left(\frac{\alpha +\beta}{2}-\alpha\right) ^3+\frac{|a|}{3}\left(\beta -\frac{\alpha +\beta}{2}\right) ^3 \\ &= 2\cdot\frac{|a|}{3}\left(\frac{\beta -\alpha}{2}\right) ^3 = \frac{|a|}{12}(\beta -\alpha )^3 \end{aligned}\] が得られる.
参考
$2$ 次関数 $f(x) = ax^2+bx+c$ について, 放物線 $C:y = f(x)$ 上に $2$ 点 $\mathrm A(\alpha,f(\alpha )),$ $\mathrm B(\beta,f(\beta ))$ $(\alpha < \beta )$ をとる.
$C$ とその弦 $\mathrm{AB}$ が囲む図形の面積 $S_1,$ および $C$ と $C$ の点 $\mathrm A,$ $\mathrm B$ における接線が囲む図形の面積 $S_2$ の比は
\[ S_1:S_2 = \frac{|a|}{6}(\beta -\alpha )^3:\frac{|a|}{12}(\beta -\alpha )^3 = 2:1\]
である.
問題《放物線と直交する接線が囲む図形の面積》
放物線 $C:y = x^2$ の点 $\mathrm A(\alpha,\alpha ^2),$ $\mathrm B(\beta,\beta ^2)$ における接線 $l,$ $m$ が直交するように点 $\mathrm A,$ $\mathrm B$ が動くとき,
$C$ と線分 $\mathrm{AB}$ で囲まれた図形の面積 $S$ の最小値を求めよ.
解答例
$y = x^2$ の導関数は, $y' = 2x$ である.
よって, 接線 $l$ の方程式は, $y = 2\alpha (x-\alpha )+\alpha ^2$ つまり
\[ y = 2\alpha x-\alpha ^2\]
である.
同様に, $m$ の方程式は,
\[ y = 2\beta x-\beta ^2\]
である.
これらが直交する条件は, $2\alpha\cdot 2\beta = -1$ つまり
\[\alpha\beta = -\frac{1}{4}\]
である.
よって, $\alpha < 0 < \beta$ として一般性を失わないから, その場合を考える.
また, 直線 $\mathrm{AB}$ の方程式は,
\[ y-\alpha ^2 = \dfrac{\beta ^2-\alpha ^2}{\beta -\alpha}(x-\alpha )\]
つまり
\[ y = (\alpha +\beta )x-\alpha\beta\]
である.
よって,
\[\begin{aligned}
S &= \int _\alpha ^\beta\{ (\alpha +\beta )x-\alpha\beta -x^2\}\,dx \\
&= -\int_\alpha^\beta (x-\alpha )(x-\beta )\,dx \\
&= -\frac{1}{6}(\beta -\alpha )^2 = \frac{1}{6}\left(\beta +\frac{1}{4\beta}\right) ^3
\end{aligned}\]
である.
したがって, 相加・相乗平均の不等式により,
\[ S \geqq \frac{1}{6}\left( 2\sqrt{\beta\cdot\frac{1}{4\beta}}\right) ^3 = \frac{1}{6}\]
である.
等号は $\alpha = -\dfrac{1}{2},$ $\beta = \dfrac{1}{2}$ のときに成り立つ.
ゆえに, 求める最小値は $\dfrac{1}{6}$ である.
問題《$3$ 次関数のグラフと $x$ 軸が囲む図形の面積》
$f(x)$ を $x^3$ の係数が $1$ である $3$ 次関数とし, そのグラフ $C:y = f(x)$ が $x$ 軸と $3$ 点 $(\alpha,0),$ $(0,0),$ $(\beta,0)$ $(\alpha > 0 > \beta )$ で交わるとする.
$C$ と $x$ 軸で囲まれた $2$ つの図形の面積の和を $S$ とおく.
- (1)
- $\alpha,$ $\beta$ を用いて $S$ を表せ.
- (2)
- $\alpha -\beta = 1$ のとき, $\alpha$ を用いて $S$ を表せ.
- (3)
- (2) のとき, $S$ を最小にする $\alpha$ の値を求めよ.
(参考: $2016$ 九州大)
解答例
- (1)
- 仮定により $f(x) = 0$ は $x = \alpha,$ $0,$ $\beta$ を解にもつから, 因数定理により $f(x)$ は \[ f(x) = x(x-\alpha )(x-\beta )\] と表せる. $C$ と $x$ 軸で囲まれる $2$ つの図形のうち, $0 \leqq x \leqq \alpha$ の部分の面積を $S_1,$ $\beta \leqq x \leqq 0$ の部分の面積を $S_2$ とおく. このとき, \[\begin{aligned} S_1 &= -\int_0^\alpha x(x-\alpha )(x-\beta )\,dx \\ &= -\int_0^\alpha\{ (x^3-(\alpha +\beta ) x^2+\alpha\beta x\}\,dx \\ &= -\left[\frac{1}{4}x^4-\frac{\alpha +\beta }{3}x^3+\frac{\alpha\beta}{2}x^2\right] _0^\alpha \\ &= -\left(\frac{1}{4}\alpha ^4-\frac{\alpha +\beta}{3}\alpha ^3+\frac{\alpha\beta}{2}\alpha ^2\right) \\ &= \frac{\alpha ^4}{12}-\frac{\alpha ^3\beta}{6} \end{aligned}\] であり, $S_2$ は $C$ を原点に関して対称移動して得られる曲線 $y = x(x+\alpha )(x+\beta )$ と $x$ 軸で囲まれる図形のうち $0 \leqq x \leqq -\beta$ の部分の面積に等しいから, \[\begin{aligned} S_2 &= -\int_0^{-\beta}x(x+\alpha )(x+\beta )\,dx \\ &= \frac{(-\beta )^4}{12}-\frac{(-\beta )^3(-\alpha )}{6} \\ &= \frac{\beta ^4}{12}-\frac{\alpha\beta ^3}{6} \end{aligned}\] である. ゆえに, 求める面積は, \[ S = S_1+S_2 = \frac{\alpha ^4}{12}-\frac{\alpha ^3\beta}{6}-\frac{\alpha\beta ^3}{6}+\frac{\beta ^4}{12} \quad \cdots [1]\] である.
- (2)
- $\alpha -\beta = 1$ のとき, $\beta = \alpha -1$ であるから, これを $[1]$ に代入して展開すると \[ S = -\frac{\alpha ^4}{6}+\frac{\alpha ^3}{3}-\frac{\alpha}{6}+\frac{1}{12}\] が得られる.
- (3)
- 仮定から, $0 < \alpha < 1$ である.
$S$ を $\alpha$ で微分すると
\[\frac{dS}{d\alpha} = -\frac{2}{3}\alpha ^3+\alpha ^2-\frac{1}{6} = -\frac{(2\alpha -1)(2\alpha ^2-2\alpha -1)}{6}\]
となるので, この範囲で $2\alpha ^2-2\alpha -1 < 0$ であることから
\[\frac{dS}{d\alpha} \geqq 0 \iff \alpha \geqq \frac{1}{2}, \quad \frac{dS}{d\alpha} \leqq 0 \iff \alpha \leqq \frac{1}{2}\]
が成り立つ.
よって, $S$ は $\alpha = \dfrac{1}{2}$ のとき極小かつ最小の値をとる.
$\alpha$ $0$ $\cdots$ $\dfrac{1}{2}$ $\cdots$ $1$ $\dfrac{dS}{d\alpha}$ $-$ $0$ $+$ $S$ $\searrow$ 極小 $\nearrow$
参考
$3$ 次関数 $f(x) = ax^3+bx^2+cx+d$ のグラフ $y = f(x)$ が $x$ 軸上の定められた閉区間 $I$ の両端とその間の $1$ 点 $\mathrm P$ で交わるようにして $b,$ $c,$ $d$ を動かすとき, $y = f(x)$ と $x$ 軸で囲まれる $2$ つの図形の面積の和は, 点 $\mathrm P$ が $I$ の中点に位置するとき最小になることが, 本問の結果と平行移動, 対称移動, 各座標軸方向の拡大・縮小によりわかる.
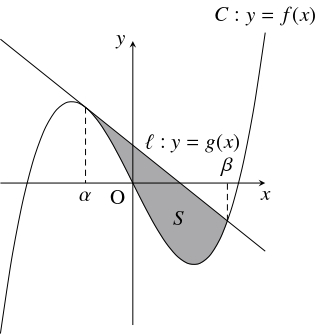
問題《$3$ 次関数のグラフと接線が囲む図形の面積》
$3$ 次関数 $f(x) = ax^3+bx^2+cx+d$ ($a,$ $b,$ $c,$ $d$: 実数) のグラフ $C:y = f(x)$ と $C$ の点 $(\alpha,f(\alpha ))$ における接線 $l :y = g(x)$ が点 $(\beta,f(\beta ))$ $(\alpha \neq \beta )$ で交わるとする.
次のことを示せ.
ただし, 多項式 $p(x)$ について, $p(\alpha ) = p'(\alpha ) = 0$ であるとき $p(x)$ が $(x-\alpha )^2$ で割り切れること (こちらを参照) は, 証明なしに使ってよい.
- (1)
- $f(x)-g(x)$ は $(x-\alpha )^2$ で割り切れる.
- (2)
- $C$ と $l$ で囲まれた図形の面積 $S$ は \[ S = \frac{|a|}{12}(\beta -\alpha )^4\] である.
解答例
- (1)
- $C:y = f(x)$ の点 $(\alpha,f(\alpha ))$ における接線 $l:y = g(x)$ の方程式は \[ y = f'(\alpha )(x-\alpha )+f(\alpha )\] であるから, \[ g(x) = f'(\alpha )(x-\alpha )+f(\alpha )\] である. \[ p(x) = f(x)-g(x) = f(x)-f(\alpha )-f'(\alpha )(x-\alpha )\] とおくと, $p(\alpha ) = 0$ であり, \[ p'(x) = f'(x)-f'(\alpha )\] から $p'(\alpha ) = 0$ となるので, $p(x) = f(x)-g(x)$ は $(x-\alpha )^2$ で割り切れる.
- (2)
- $C$ と $l$ は点 $(\beta,f(\beta ))$ で交わるから, $f(\beta )-g(\beta ) = 0$ である.
よって, (1) の結果と因数定理により,
\[ f(x)-g(x) = a(x-\alpha )^2(x-\beta )\]
が成り立つ.
ゆえに,
\[\begin{aligned}
S &= \left|\int_\alpha ^\beta |f(x)-g(x)|\,dx\right| \\
&= |a|\left|\int_\alpha ^\beta (x-\alpha )^2(\beta -x)\,dx\right| \\
&= |a|\left|\int_\alpha ^\beta (x-\alpha )^2\{ (\beta -\alpha )+(\alpha -x)\}\,dx\right| \\
&= |a|\left|\int_\alpha ^\beta\{ (\beta -\alpha )(x-\alpha )^2-(x-\alpha )^3\}\,dx\right| \\
&= |a|\left|\left[ (\beta -\alpha )\frac{(x-\alpha )^3}{3}-\frac{(x-\alpha )^4}{4}\right] _\alpha ^\beta\right| \\
&= |a|\left|\frac{(\beta -\alpha )^4}{3}-\frac{(\beta -\alpha )^4}{4}\right| \\
&= \frac{|a|}{12}(\beta -\alpha )^4
\end{aligned}\]
が成り立つ.
問題《$4$ 次関数のグラフと接線が囲む図形の面積》
$4$ 次関数 $f(x) = ax^4+bx^3+cx^2+dx+e$ ($a,$ $b,$ $c,$ $d,$ $e$: 実数) のグラフ $C:y = f(x)$ と直線 $l:y = g(x)$ が $2$ 点 $(\alpha,f(\alpha )),$ $(\beta,f(\beta ))$ $(\alpha < \beta )$ で接するとする.
$C$ と $l$ が囲む図形の面積 $S$ は
\[ S = \dfrac{|a|}{30}(\beta -\alpha )^5\]
であることを示せ.
ただし, 多項式関数 $y = f(x)$ のグラフと直線 $y = g(x)$ が点 $(\alpha,f(\alpha ))$ で接するとき $f(x)-g(x)$ が $(x-\alpha )^2$ で割り切れることは, 証明なしに使ってよい.
解答例
$f(x)-g(x) = a(x-\alpha )^2(x-\beta )^2$ であるから,
\[\begin{aligned}
S &= \left|\int_\alpha ^\beta |f(x)-g(x)|\,dx\right| \\
&= |a|\left|\int_\alpha ^\beta (x-\alpha )^2(x-\beta ) ^2\,dx\right| \\
&= |a|\left|\int_\alpha ^\beta (x-\alpha )^2\{ (x-\alpha )-(\beta -\alpha )\} ^2\,dx\right| \\
&= |a|\left|\int_\alpha ^\beta\{ (x\!-\!\alpha )^4\!-\!2(\beta\!-\!\alpha )(x\!-\!\alpha )^3\!+\!(\beta\!-\!\alpha )^2(x\!-\!\alpha )^2\}\,dx\right| \\
&= |a|\left|\left[\frac{(x-\alpha )^5}{5}-2(\beta -\alpha )\frac{(x-\alpha )^4}{4}+(\beta -\alpha )^2\frac{(x-\alpha )^3}{3}\right] _\alpha ^\beta\right| \\
&= |a|\left|\frac{(\beta -\alpha )^5}{5}-\frac{(\beta -\alpha )^5}{2}+\frac{(\beta -\alpha )^5}{3}\right| \\
&= \frac{|a|}{30}(\beta -\alpha )^5
\end{aligned}\]
が成り立つ.
参考
一般に, 実数 $\alpha,$ $\beta,$ 非負整数 $m,$ $n$ に対して
\[\int_\alpha ^\beta (x-\alpha )^m(\beta -x)^n\,dx = \frac{m!n!}{(m+n+1)!}(\beta -\alpha )^{m+n+1}\]
が成り立つ (こちらを参照).
