$2$ 次曲線
放物線
こちらを参照.
楕円の周
こちらを参照.
双曲線
こちらを参照.
$2$ 次曲線
問題《円錐曲線の名の由来》
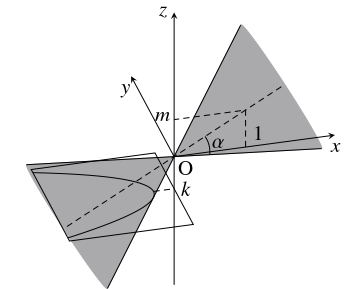
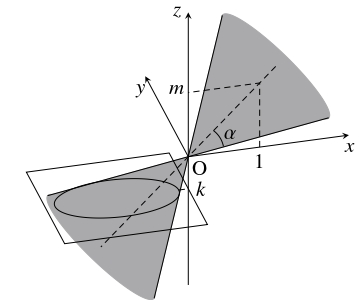
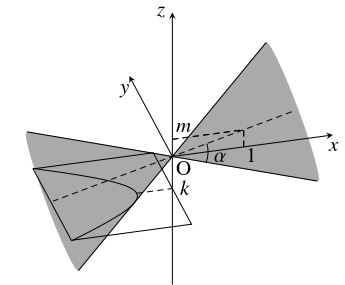
座標空間において, 原点 $\mathrm O$ を通って $\vec d = (1,0,m)$ $(m > 0)$ に平行な直線を軸とする円錐面 (底面は考えない) において, 軸と母線のなす角を $\alpha\ \left( 0 < \alpha < \dfrac{\pi}{2}\right)$ とおく.
このとき, 円錐面は $\vec d\cdot\overrightarrow{\mathrm{OP}} = |\vec d||\overrightarrow{\mathrm{OP}}|\cos\alpha$ を満たす点 $\mathrm P$ の集合になる.
これを平面 $z = k$ ($k$: 実数, $k \neq 0$) で切断するとき, 断面にはどのような曲線が現れるか.
次の $3$ つの場合に分けて答えよ.
- (i)
- $\tan\alpha = m$ のとき. (ii) $\tan\alpha < m$ のとき.
- (iii)
- $\tan\alpha > m$ のとき.
解答例
点 $\mathrm P(x,y,z)$ が円錐面上にあるとする.
このとき, $\vec d\cdot\overrightarrow{\mathrm{OP}} = |\vec d||\overrightarrow{\mathrm{OP}}|\cos\alpha$ から,
\[\begin{aligned}
(\vec d\cdot\overrightarrow{\mathrm{OP}})^2 &= |\vec d|^2|\overrightarrow{\mathrm{OP}}|^2\cos ^2\alpha \\
(x+mz)^2 &= (1+m^2)(x^2+y^2+z^2)\cos ^2\alpha
\end{aligned}\]
が成り立つ.
この点 $\mathrm P$ が平面 $z = k$ 上にあるとき,
\[\begin{aligned}
&(x+mk)^2 = (1+m^2)(x^2+y^2+k^2)\cos ^2\alpha, \\
&\{ (1+m^2)\cos ^2\alpha -1\} x^2-2mkx+(1+m^2)\cos ^2\alpha\cdot y^2 \\
&\qquad\qquad\qquad\qquad\qquad\quad = \{ m^2-(1+m^2)\cos ^2\alpha\} k^2, \\
&(m^2\cos ^2\alpha -\sin ^2\alpha )x^2-2mkx+(1+m^2)\cos ^2\alpha\cdot y^2 \\
&\qquad\qquad\qquad\qquad\qquad\qquad\quad = (m^2\sin ^2\alpha -\cos ^2\alpha )k^2
\end{aligned}\]
が成り立つ.
\[\begin{aligned}
A &= m^2\cos ^2\alpha -\sin ^2\alpha, \\
B &= (1+m^2)\cos ^2\alpha, \\
C &= m^2\sin ^2\alpha -\cos ^2\alpha
\end{aligned}\]
とおくと, これは
\[ Ax^2-2mkx+By^2 = Ck^2 \quad \cdots [1]\]
と表される.
- (i)
- $\tan\alpha = m$ のとき.
$A = 0$ から
\[ [1] \iff x = \frac{B}{2mk}y^2-\frac{Ck}{2m}\]
であるので, 切断面は放物線になる.
- (ii)
- $\tan\alpha < m$ のとき.
$[2]$ において $A > 0$ よって $A^2 > 0,$ $AB > 0$ であるから, 切断面は楕円の周である.
- (iii)
- $\tan\alpha > m$ のとき.
$[2]$ において $A < 0$ よって $A^2 > 0,$ $AB < 0$ であるから, 切断面は双曲線である.
参考
本問で見た通り, $2$ 次曲線 (放物線, 円・楕円の周, 双曲線) は, 円錐面を平面で切断したときに現れるため,「円錐曲線」と呼ばれる.
(i) の母線と平行な平面で切断する場合には放物線が現れ,
(ii) の軸に対して母線より深い角で交わる平面で切断する場合には円・楕円の周が現れ,
(iii) の軸に対して母線より浅い角で交わる平面で切断する場合には双曲線が現れる.
問題《$2$ 次曲線の離心率》
$c > 0,$ $e > 0$ とする.
定点 $\mathrm F(c,0)$ と $y$ 軸からの距離の比が $e:1$ である点 $\mathrm P$ の軌跡とその方程式を求めよ.
解答例
点 $\mathrm P$ の座標を $(x,y),$ 点 $\mathrm P$ から $y$ 軸に下ろした垂線の足を $\mathrm H$ とおき, 点 $\mathrm P$ の軌跡を $C$ とおく.
このとき,
\[\begin{aligned}
\mathrm P \in C &\iff \mathrm{FP}:\mathrm{HP} = e:1 \\
&\iff \mathrm{FP} = e\mathrm{HP} \\
&\iff \mathrm{FP}^2 = e^2\mathrm{HP}^2 \\
&\iff (x-c)^2+y^2 = e^2x^2 \\
&\iff (1-e^2)x^2-2cx+y^2+c^2 = 0 \quad \cdots [\ast ]
\end{aligned}\]
となる.
- (i)
- $e = 1$ のとき. $[\ast ]$ は, $y^2 = 2cx-c^2$ となるから, 放物線を表す.
- (ii)
- $e \neq 1$ のとき. $[\ast ]$ は \[\frac{\left( x-\dfrac{c}{1-e^2}\right) ^2}{\dfrac{c^2e^2}{(1-e^2)^2}}+\frac{y^2}{\dfrac{c^2e^2}{1-e^2}} = 1\] と変形できる. よって, $\dfrac{c^2e^2}{(1-e^2)^2} > 0$ に注意すると, $[\ast ]$ は, $0 < e < 1\ \left(\dfrac{c^2e^2}{1-e^2} > 0\right)$ のとき楕円を表し, $e > 1\ \left(\dfrac{c^2e^2}{1-e^2} < 0\right)$ のとき双曲線を表す.
