楕円の周
楕円の周
定義《楕円》
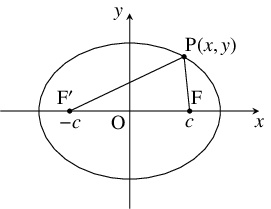
平面上で, 相異なる $2$ 定点 $\mathrm F,$ $\mathrm F'$ からの距離の和が一定値 $2a$ $(a > 0)$ 以下である点の存在範囲を楕円 (ellipse) と呼ぶ.
その境界, つまり $\mathrm F,$ $\mathrm F'$ からの距離の和が $2a$ である点の軌跡 $C$ を楕円の周 (circumference) と呼び, $\mathrm F,$ $\mathrm F'$ を焦点(focus) と呼ぶ.
直線 $\mathrm{FF}'$ の $C$ によって切り取られる部分の線分を $C$ の長軸 (major axis),
長軸の垂直二等分線の $C$ によって切り取られる部分の線分を $C$ の短軸 (minor axis) と呼ぶ.
また, 長軸と短軸の交点を $C$ の中心 (center) と呼び, 長軸と短軸の各端点を頂点 (vertex) と呼ぶ.
定理《楕円の周の標準形》
$a,$ $b > 0$ とする.
楕円の周 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ の中心は原点であり, $C$ は $x$ 軸, $y$ 軸, 原点に関して対称である.
- (i)
- $a > b$ のとき. $C$ の焦点は $(\pm\sqrt{a^2-b^2},0),$ 長軸の長さは $2a,$ 短軸の長さは $2b$ であり, $C$ の $2$ つの焦点から $C$ の各点までの距離の和は $2a$ である.
- (ii)
- $a < b$ のとき. $C$ の焦点は $(0,\pm\sqrt{b^2-a^2}),$ 長軸の長さは $2b,$ 短軸の長さは $2a$ であり, $C$ の $2$ つの焦点から $C$ の各点までの距離の和は $2b$ である.
証明
(i), (ii) は互いに $x$ 座標, $y$ 座標を入れ替えた関係にあるから, (i) について, $c > 0$ として, 点 $\mathrm F(c,0),$ $\mathrm F'(-c,0)$ からの距離の和が $2a$ $(a > c)$ である点の軌跡 $C$ を求める.
$b = \sqrt{a^2-c^2}$ とおくと, 平面上の点 $\mathrm P(x,y)$ に対して,
\[\begin{aligned}
&\mathrm P \in C \\
&\iff \mathrm{PF}+\mathrm{PF}' = 2a \iff \mathrm{PF} = 2a-\mathrm{PF}' \\
&\iff \mathrm{PF}^2 = (2a-\mathrm{PF}')^2 \iff \mathrm{PF}^2 = 4a^2-4a\mathrm{PF}'+\mathrm{PF}'^2 \\
&\iff (x-c)^2+y^2 = 4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \\
&\iff cx+a^2 = a\sqrt{(x+c)^2+y^2} \\
&\iff (cx+a^2)^2 = a^2\{ (x+c)^2+y^2\} \\
&\iff (a^2-c^2)x^2+a^2y^2 = a^2(a^2-c^2) \\
&\iff b^2x^2+a^2y^2 = a^2b^2 \iff \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1
\end{aligned}\]
となるから, $C$ の方程式は $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ である.
$(x,y) \in C$ のとき $(x,-y),$ $(-x,y),$ $(-x,-y) \in C$ となるから, $C$ は $x$ 軸, $y$ 軸, 原点に関して対称である. $c = \sqrt{a^2-b^2}$ であるから, $C$ の焦点は $(\pm\sqrt{a^2-b^2},0)$ である.
また, $C$ の座標軸との交点は $(\pm a,0),$ $(0,\pm b)$ であるから, 長軸の長さは $2a,$ 短軸の長さは $2b$ である.
$(x,y) \in C$ のとき $(x,-y),$ $(-x,y),$ $(-x,-y) \in C$ となるから, $C$ は $x$ 軸, $y$ 軸, 原点に関して対称である. $c = \sqrt{a^2-b^2}$ であるから, $C$ の焦点は $(\pm\sqrt{a^2-b^2},0)$ である.
また, $C$ の座標軸との交点は $(\pm a,0),$ $(0,\pm b)$ であるから, 長軸の長さは $2a,$ 短軸の長さは $2b$ である.
定理《楕円の周の接線》
楕円の周 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ $(a,\ b > 0)$ の $C$ 上の点 $\mathrm P_0(x_0,y_0)$ における接線の方程式は
\[\frac{x_0x}{a^2}+\frac{y_0y}{b^2} = 1\]
である.
証明
$\mathrm P_0 \neq (\pm a,0)$ のとき, $C$ の点 $\mathrm P_0$ における接線の傾きを $m$ とおく.
$C$ の方程式 $b^2x^2+a^2y^2 = a^2b^2$ と接線の方程式
\[ y = mx+y_0-mx_0\]
から $y$ を消去して得られる $2$ 次方程式
\[ b^2x^2+a^2(mx+y_0-mx_0)^2 = a^2b^2\]
つまり
\[\begin{aligned}
(b^2+a^2m^2)x^2&+2a^2m(y_0-mx_0)x \\
&+a^2\{(y_0-mx_0)^2-b^2\} = 0
\end{aligned}\]
は重解 $x = x_0$ をもつから,
\[\begin{aligned}
-\frac{a^2m(y_0-mx_0)}{b^2+a^2m^2} &= x_0 \\
-a^2m(y_0-mx_0) &= (b^2+a^2m^2)x_0 \\
m &= -\dfrac{b^2x_0}{a^2y_0}
\end{aligned}\]
となる.
よって, 接線の方程式は
\[\begin{aligned}
y-y_0 &= -\dfrac{b^2x_0}{a^2y_0}(x-x_0) \\
\frac{b^2x_0x}{a^2y_0}+y &= \frac{b^2x_0{}^2}{a^2y_0}+y_0 \\
\frac{x_0x}{a^2}+\frac{y_0y}{b^2} &= \frac{x_0{}^2}{a^2}+\frac{y_0{}^2}{b^2} \\
\frac{x_0x}{a^2}+\frac{y_0y}{b^2} &= 1
\end{aligned}\]
である.
$\mathrm P_0 = (\pm a,0)$ のときの $C$ の接線の方程式 $x = \pm a$ もこの式で表される.
別証明
$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ の両辺を $x$ で微分すると, $\dfrac{2x}{a^2}+\dfrac{2yy'}{b^2} = 0$ となり, $y \neq 0$ のとき
\[ y' = -\frac{b^2x}{a^2y}\]
となる.
よって, $\mathrm P_0 \neq (\pm a,0)$ のとき, $C$ の点 $\mathrm P_0$ における接線の傾きは $-\dfrac{b^2x_0}{a^2y_0}$ である.
以下, 上記の証明と同様である.
問題《楕円の特徴付け》
- (A)
- $a > c > 0$ とする. $2$ 点 $\mathrm F(c,0),$ $\mathrm F'(-c,0)$ からの距離の和が $2a$ であるような点 $\mathrm P$ の軌跡の方程式を求めよ.
- (B)
- $a,$ $b$ を正の数とする. $x$ 軸上の点 $\mathrm P$ と $y$ 軸上の点 $\mathrm Q$ が $\mathrm{PQ} = a+b$ を満たしながら動くとき, 線分 $\mathrm{PQ}$ を $b:a$ に内分する点 $\mathrm R$ の軌跡の方程式を求めよ.
- (C)
- 単位円周を $x$ 軸方向に $a$ 倍に, $y$ 軸方向に $b$ 倍に拡大または縮小した曲線の方程式を求めよ.
解答例
- (A)
- \[\begin{aligned}
&\mathrm{FP}+\mathrm F'\mathrm P = 2a \\
&\iff \mathrm{FP} = 2a-\mathrm F'\mathrm P \\
&\iff \sqrt{(x-c)^2+y^2} = 2a-\sqrt{(x+c)^2+y^2} \\
&\iff (x-c)^2+y^2 \\
&\qquad\quad = 4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \\
&\iff 4a\sqrt{(x+c)^2+y^2} = 4cx+4a^2 \\
&\iff a\sqrt{(x+c)^2+y^2} = cx+a^2 \\
&\iff a^2(x+c)^2+a^2y^2 = c^2x^2+2a^2cx+a^4 \\
&\iff (a^2-c^2)x^2+a^2y^2 = a^2(a^2-c^2) \\
&\iff \frac{x^2}{a^2}+\frac{y^2}{a^2-c^2} = 1
\end{aligned}\]
から, 点 $\mathrm P$ の軌跡の方程式は $\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2-c^2} = 1$ である.
- (B)
- $\mathrm P(p,0),$ $\mathrm Q(0,q),$ $\mathrm R(x,y)$ とおく.
このとき, 条件 $\mathrm{PQ} = a+b$ から, \[ p^2+q^2 = (a+b)^2 \quad \cdots [1]\] が成り立つ. また, 点 $\mathrm R$ は線分 $\mathrm{PQ}$ を $b:a$ に内分する点であるから, \[ x = \frac{a}{a+b}p, \quad y = \frac{b}{a+b}q\] が成り立つ. よって, \[ p = \frac{a+b}{a}x, \quad q = \frac{a+b}{b}y \quad \cdots [2]\] であるから, $[1]$ に $[2]$ を代入すると \[\frac{(a+b)^2}{a^2}x^2+\frac{(a+b)^2}{b^2}y^2 = (a+b)^2\] となり, 点 $\mathrm R$ の軌跡の方程式 \[\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1\] が得られる.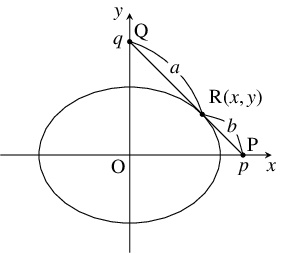
- (C)
- 単位円周を $x$ 軸方向に $a$ 倍に, $y$ 軸方向に $b$ 倍に拡大または縮小するとき, 点 $(X,Y)$ が点 $(x,y)$ に移るとする.
このとき,
\[ X^2+Y^2 = 1, \quad x = aX, \quad y = bY\]
が成り立つから, $X^2+Y^2 = 1$ に $X = \dfrac{x}{a},$ $Y = \dfrac{y}{b}$ を代入すると, 求める曲線の方程式
\[\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1\]
が得られる.
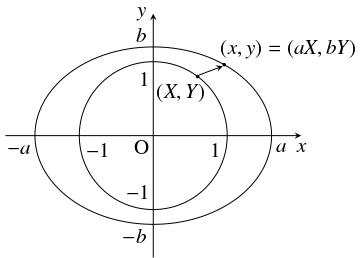
参考
(A) のように $2$ 定点からの距離の和が一定である点の軌跡が楕円の周の定義であるが,
(B), (C) のように楕円を定めることもできる.
問題《楕円に内接する三角形の面積の最大値》
$p,$ $q$ を正の数とする.
楕円の周 $\dfrac{x^2}{p^2}+\dfrac{y^2}{q^2} = 1$ に内接する三角形の面積の最大値を求めよ.
解答例
楕円の周 $\dfrac{x^2}{p^2}+\dfrac{y^2}{q^2} = 1$ は単位円周 $x^2+y^2 = 1$ を $x$ 軸方向に $p$ 倍, $y$ 軸方向に $q$ 倍に拡大した図形であるから, 単位円, この楕円に内接する三角形の面積の最大値 $M,$ $M'$ の間には
\[ M' = pqM \]
という関係がある.
そこで, 単位円に内接する三角形 $\mathrm{ABC}$ の面積 $S$ の最大値 $M$ を求める. $\cdots [*]$
$a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB}$ とおく. 正弦定理により \[\sin A = \frac{a}{2} \quad \cdots [1]\] であるから, \[ S = \frac{1}{2}bc\sin A = \frac{abc}{4}\] が成り立つ. 相加・相乗平均の関係 \[\sqrt[3]{xyz} \leqq \frac{x+y+z}{3} \quad \cdots [2]\] を $x = a^3,$ $y = b^3,$ $z = c^3$ (いずれも正の数) に適用すると, \[ abc = \sqrt[3]{a^3b^3c^3} \leqq \frac{a^3+b^3+c^3}{3} \quad \cdots [3] \] が得られる. $[2]$ の等号成立条件は $x = y = z$ であるから, $[3]$ で等号が成立するのは $a = b = c$ の場合に限る. $a = b = c$ のとき, $3$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ は正三角形を成し, $[1]$ から $a = 2\sin 60^\circ = \sqrt 3$ であるので, \[ abc = \dfrac{3a^3}{3} = a^3 = 3\sqrt 3\] が成り立つ. よって, これが $abc$ の最大値である. 以上から, $S$ の最大値は \[ M = \frac{3\sqrt 3}{4}\] であり, 求める最大値は \[ M' = \frac{3\sqrt 3}{4}pq\] である.
$a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB}$ とおく. 正弦定理により \[\sin A = \frac{a}{2} \quad \cdots [1]\] であるから, \[ S = \frac{1}{2}bc\sin A = \frac{abc}{4}\] が成り立つ. 相加・相乗平均の関係 \[\sqrt[3]{xyz} \leqq \frac{x+y+z}{3} \quad \cdots [2]\] を $x = a^3,$ $y = b^3,$ $z = c^3$ (いずれも正の数) に適用すると, \[ abc = \sqrt[3]{a^3b^3c^3} \leqq \frac{a^3+b^3+c^3}{3} \quad \cdots [3] \] が得られる. $[2]$ の等号成立条件は $x = y = z$ であるから, $[3]$ で等号が成立するのは $a = b = c$ の場合に限る. $a = b = c$ のとき, $3$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ は正三角形を成し, $[1]$ から $a = 2\sin 60^\circ = \sqrt 3$ であるので, \[ abc = \dfrac{3a^3}{3} = a^3 = 3\sqrt 3\] が成り立つ. よって, これが $abc$ の最大値である. 以上から, $S$ の最大値は \[ M = \frac{3\sqrt 3}{4}\] であり, 求める最大値は \[ M' = \frac{3\sqrt 3}{4}pq\] である.
$[*]$ 以降の別解
$A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C$ とおく.
正弦定理により
\[\frac{\mathrm{AC}}{\sin B} = \frac{\mathrm{AB}}{\sin C} = 2\]
であるから,
\[\begin{aligned}
S &= \frac{1}{2}\mathrm{AB}\cdot\mathrm{AC}\sin A = \sin A\cdot 2\sin B\sin C \\
&= \sin A\{\cos (B-C)-\cos (B+C)\} \\
&= \sin A\{\cos (B-C)+\cos A\} \quad (\because B+C = \pi -A)
\end{aligned}\]
が成り立つ.
点 $\mathrm A$ を固定すると, $\cos (B-C) = 1$ すなわち $B = C$ のとき $S$ は最大となる.
よって,
\[ S \leqq \sin A(1+\cos A) = \sin A+\frac{1}{2}\sin 2A\]
が成り立つ.
右辺を $f(A)$ とおく.
このとき,
\[\begin{aligned}
f'(A) &= \cos A+\cos 2A = 2\cos ^2A+\cos A-1 \\
&= (\cos A+1)(2\cos A-1)
\end{aligned}\]
から
\[\begin{aligned}
f'(A) \geqq 0 &\iff 2\cos A-1 \geqq 0 \iff A \leqq \frac{\pi}{3}, \\
f'(A) \leqq 0 &\iff A \geqq \frac{\pi}{3}
\end{aligned}\]
となる.
よって, $f(A)$ は $A = \dfrac{\pi}{3}$ のとき極大かつ最大の値をとるから, $S$ は $A = B = C = \dfrac{\pi}{3}$ すなわち $\triangle\mathrm{ABC}$ が正三角形のとき最大値
\[ M = 2\left(\sin\frac{\pi}{3}\right)^3 = \frac{3\sqrt 3}{4}\]
をとる.
ゆえに, 求める最大値は,
\[ M' = \frac{3\sqrt 3}{4}pq\]
である.
| $A$ | $0$ | $\cdots$ | $\dfrac{\pi}{3}$ | $\cdots$ | $\pi$ |
| $f'(A)$ | $+$ | $0$ | $-$ | ||
| $f(A)$ | $\nearrow$ | 極大 | $\searrow$ |
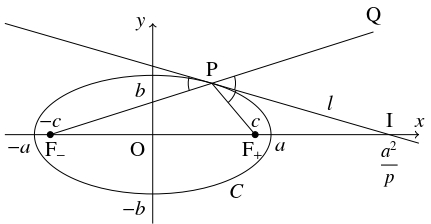
問題《楕円の焦点から発せられた光の反射》
楕円の周 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ $(a > b > 0)$ の焦点を $\mathrm F_+(c,0),$ $\mathrm F_-(-c,0)$ $(c > 0)$ とおき,
$C$ 上に点 $\mathrm P(p,q)$ $(p \geqq 0)$ をとる.
- (1)
- $a,$ $c,$ $p$ を用いて線分 $\mathrm F_+\mathrm P,$ $\mathrm F_-\mathrm P$ の長さを表せ.
- (2)
- $C$ の点 $\mathrm P$ における接線 $l$ と線分 $\mathrm F_+\mathrm P,$ $\mathrm F_-\mathrm P$ のなす角は等しいことを示せ.
解答例
- (1)
- $\dfrac{p^2}{a^2}+\dfrac{q^2}{b^2} = 1,$ $c^2 = a^2-b^2$ から, \[\begin{aligned} \mathrm F_\pm\mathrm P^2 &= (p\mp c)^2+q^2 = p^2\mp 2cp+c^2+b^2\left( 1-\frac{p^2}{a^2}\right) \\ &= \left( 1-\frac{b^2}{a^2}\right) p^2\mp 2cp+(c^2+b^2) \\ &= \frac{c^2}{a^2}p^2\mp 2cp+a^2 = \left( a\mp\frac{c}{a}p\right) ^2 \end{aligned}\] である. $-a \leqq p \leqq a$ から \[ a\mp\frac{c}{a}p \geqq a \mp\frac{c}{a}\cdot (\pm a) = a-c > 0\] であるので, \[\mathrm F_\pm\mathrm P = a\mp\frac{c}{a}p\] である (以上, 複号同順).
- (2)
- 点 $\mathrm P$ が $C$ の頂点である場合, $l$ と線分 $\mathrm F_+\mathrm P,$ $\mathrm F_-\mathrm P$ のなす角は明らかに等しい.
よって, その他の場合を考える.
このとき,
\[ l:\dfrac{px}{a^2}+\dfrac{qy}{b^2} = 1\]
と $x$ 軸の交点を $\mathrm I$ とおくと,
$\mathrm I\left(\dfrac{a^2}{p},0\right)$ から
\[\begin{aligned}
\mathrm F_+\mathrm I:\mathrm F_-\mathrm I &= \left(\frac{a^2}{p}-c\right) :\left(\frac{a^2}{p}+c\right) \\
&= (a^2-cp):(a^2+cp)
\end{aligned}\]
であり, (1) の結果により
\[\begin{aligned}
\mathrm F_+\mathrm P:\mathrm F_-\mathrm P &= \left( a-\frac{c}{a}p\right) :\left( a+\frac{c}{a}p\right) \\
&= (a^2-cp):(a^2+cp)
\end{aligned}\]
が成り立つので, $\mathrm F_+\mathrm I:\mathrm F_-\mathrm I = \mathrm F_+\mathrm P:\mathrm F_-\mathrm P$ となる.
したがって, 点 $\mathrm P$ に関して $\mathrm F_-$ と対称な点を $\mathrm Q$ とおくと,
$l$ は $\angle\mathrm F_+\mathrm P\mathrm Q$ を二等分するから,
$l$ と線分 $\mathrm F_+\mathrm P,$ $\mathrm F_-\mathrm P$ のなす角は等しい.
参考
楕円の焦点から発せられ, 楕円の周で反射した光は, もう $1$ つの焦点を通る.
この原理は, 反射望遠鏡に応用されている.

問題《楕円の接線の長さの最小値》
$a,$ $b$ を正の数とする.
楕円の周 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ の接線が座標軸により切り取られてできる線分の長さの最小値を求めよ.
解答例
楕円の周 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ の点 $(a\cos\theta,b\sin\theta )$ における接線の方程式は,
である.
この接線が座標軸と $2$ 点で交わるとき, 対称性により $0 < \theta < \dfrac{\pi}{2}$ の場合を考えれば十分であり,
そのときの交点は $\mathrm P\left(\dfrac{a}{\cos\theta},0\right),$ $\mathrm Q\left( 0,\dfrac{b}{\sin\theta}\right)$ である.
$a > 0,$ $b > 0,$ $\tan\theta > 0$ に注意すると,
相加・相乗平均の関係により,
\[\begin{aligned}
\mathrm{PQ}^2 &= \frac{a^2}{\cos ^2\theta}+\frac{b^2}{\sin ^2\theta} \\
&= a^2(1+\tan ^2\theta )+b^2\left( 1+\frac{1}{\tan ^2\theta}\right) \\
&= a^2+b^2+a^2\tan ^2\theta +\frac{b^2}{\tan ^2\theta} \\
&\geqq a^2+b^2+2\sqrt{a^2\tan ^2\theta\cdot\frac{b^2}{\tan ^2\theta}} \\
&= a^2+b^2+2ab = (a+b)^2
\end{aligned}\]
が成り立つ.
等号は $a^2\tan ^2\theta = \dfrac{b^2}{\tan ^2\theta}$ すなわち $\tan\theta = \sqrt{\dfrac{b}{a}}$ のとき成り立つ.
ゆえに, 線分 $\mathrm{PQ}$ の長さの最小値は, $a+b$ である.
| $\dfrac{a\cos\theta}{a^2}x+\dfrac{b\sin\theta}{b^2}y = 1$ つまり $\dfrac{\cos\theta}{a}x+\dfrac{\sin\theta}{b}y = 1$ |
問題《楕円の接線と座標軸が囲む三角形の面積》
$a,$ $b$ を正の数とする.
楕円の周 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ の接線と座標軸で囲まれる三角形の面積の最小値を求めよ.
解答例
楕円の周 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ の点 $(a\cos\theta,b\sin\theta )$ における接線の方程式は,
である.
この接線が座標軸と $2$ 点で交わるとき, 対称性により $0 < \theta < \dfrac{\pi}{2}$ の場合を考えれば十分であり,
そのときの交点は $\mathrm P\left(\dfrac{a}{\cos\theta},0\right),$ $\mathrm Q\left( 0,\dfrac{b}{\sin\theta}\right)$ である.
このとき,
\[\triangle\mathrm{OPQ} = \frac{1}{2}\cdot\frac{a}{\cos\theta}\cdot\frac{b}{\sin\theta} = \frac{ab}{2\cos\theta\sin\theta} = \frac{ab}{\sin 2\theta}\]
である.
$0 < \theta < \dfrac{\pi}{2}$ から $0 < 2\theta < \pi$ であるので, $\sin 2\theta$ は $2\theta = \dfrac{\pi}{2}$ つまり $\theta = \dfrac{\pi}{4}$ のとき最大値 $1$ をとる.
よって, $\triangle\mathrm{OPQ}$ の最小値は $ab$ である.
| $\dfrac{a\cos\theta}{a^2}x+\dfrac{b\sin\theta}{b^2}y = 1$ つまり $\dfrac{\cos\theta}{a}x+\dfrac{\sin\theta}{b}y = 1$ |
別解
楕円の周 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ の点 $(p,q)$ における接線の方程式は,
\[\frac{p}{a^2}x+\frac{q}{b^2}y = 1\]
である.
この接線が座標軸と $2$ 点で交わるとき, 対称性により $p > 0,$ $q > 0$ の場合を考えれば十分であり,
そのときの交点は $\mathrm P\left(\dfrac{a^2}{p},0\right),$ $\mathrm Q\left( 0,\dfrac{b^2}{q}\right)$ である.
このとき,
\[\triangle\mathrm{OPQ} = \frac{1}{2}\cdot\frac{a^2}{p}\cdot\frac{b^2}{q} = \frac{a^2b^2}{2}\cdot\frac{1}{pq} \quad \cdots [1]\]
である.
$a > 0,$ $b > 0,$ $p > 0,$ $q > 0$ に注意すると,
相加・相乗平均の関係により,
\[\begin{aligned}
&1 = \frac{p^2}{a^2}+\frac{q^2}{a^2} \geqq 2\sqrt{\frac{p^2}{a^2}\cdot\frac{q^2}{a^2}} = 2\frac{pq}{ab} \\
&\frac{1}{pq} \geqq \frac{2}{ab} \quad \cdots [2]
\end{aligned}\]
が成り立ち, 等号は $\dfrac{p^2}{a^2} = \dfrac{q^2}{a^2}$ つまり $p = \dfrac{a}{\sqrt 2},$ $q = \dfrac{b}{\sqrt 2}$ のときに成り立つ.
よって, $[1],$ $[2]$ から,
\[\triangle\mathrm{OPQ} \geqq \frac{a^2b^2}{2}\cdot\frac{2}{ab} = ab\]
が得られる.
ゆえに, $\triangle\mathrm{OPQ}$ の最小値は $ab$ である.
問題《楕円に外接する長方形の面積の最大値》
$a,$ $b$ を正の数とする.
楕円の周 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ に $4$ 辺が接する長方形 $R$ を考える.
- (1)
- $R$ の対角線の長さ $L$ は $R$ のとり方によらず一定であることを示せ.
- (2)
- $R$ の面積 $S$ の最大値を求めよ.
(参考: 岩手大)
解答例
- (1)
- $l:y = mx+n$ ($m,$ $n$: 実数) を $C:b^2x^2+a^2y^2-a^2b^2 = 0$ の接線とする.
このとき, 接点の $x$ 座標は $x$ の $2$ 次方程式
\[\begin{aligned}
b^2x^2+a^2(mx+n)^2-a^2b^2 &= 0 \\
(a^2m^2+b^2)x^2+2a^2mnx+a^2(n^2-b^2) &= 0 \quad \cdots [1]
\end{aligned}\]
の重解であり, $[1]$ の判別式 $D$ について
\[\frac{D}{4} = a^4m^2n^2-(a^2m^2+b^2)a^2(n^2-b^2) = 0\]
が成り立つから,
である. $m \neq 0$ のとき, 原点と接線 \[ l:mx-y\pm\sqrt{a^2m^2+b^2} = 0\] の距離を $d(m)$ とおくと, \[ d(m) = \frac{|\pm\sqrt{a^2m^2+b^2}|}{\sqrt{m^2+1}} = \sqrt{\frac{a^2m^2+b^2}{m^2+1}}\] となる. よって, $R$ の辺の傾きが $m,$ $-m^{-1}$ $(m \neq 0)$ であるとき, その対角線の長さは \[\begin{aligned} L &= 2\sqrt{d(m)^2+d(-m^{-1})^2} \\ &= 2\sqrt{\frac{a^2m^2+b^2}{m^2+1}+\frac{a^2m^{-2}+b^2}{m^{-2}+1}} \\ &= 2\sqrt{\frac{a^2m^2+b^2}{m^2+1}+\frac{a^2+b^2m^2}{1+m^2}} \\ &= 2\sqrt{\frac{(m^2+1)(a^2+b^2)}{m^2+1}} \\ &= 2\sqrt{a^2+b^2} \end{aligned}\] であり, $R$ のとり方によらず一定である.
$-a^2b^2(-a^2m^2+n^2-b^2) = 0$ つまり $n = \pm\sqrt{a^2m^2+b^2}$ これは, $R$ の各辺が座標軸に平行なとき, つまり $R$ が $4$ 直線 $x = \pm a,$ $y = \pm b$ の囲む長方形であるときも含めて成り立つ.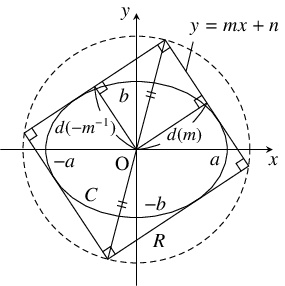
- (2)
- (i)
- $R$ の各辺が座標軸に平行なとき. $R$ の面積は \[ S = 2a\cdot 2b = 4ab\] である.
- (ii)
- $R$ の辺の傾きが $m,$ $-m^{-1}$ $(m \neq 0)$ であるとき. $R$ の面積は \[\begin{aligned} S &= 2d(m)\cdot 2d(-m^{-1}) \\ &= 4\sqrt{\frac{a^2m^2+b^2}{m^2+1}}\sqrt{\frac{a^2m^{-2}+b^2}{m^{-2}+1}} \\ &= 4\sqrt{\frac{a^4+b^4+a^2b^2(m^2+m^{-2})}{m^2+2+m^{-2}}} \\ &= 4\sqrt{\frac{a^4-2a^2b^2+b^4+a^2b^2(m^2+2+m^{-2})}{m^2+2+m^{-2}}} \\ &= 4\sqrt{\frac{(a^2-b^2)^2}{(m+m^{-1})^2}+a^2b^2} \\ &\leqq 4\sqrt{\frac{(a^2-b^2)^2}{4}+a^2b^2} = 4\sqrt{\frac{(a^2+b^2)^2}{4}} \\ &= 2(a^2+b^2) \end{aligned}\] である. 不等号は \[ m+m^{-1} \geqq 2\sqrt{m\cdot m^{-1}} = 2\] から従い, その等号は $m = m^{-1},$ $m^2 = 1$ つまり $m = \pm 1$ のとき成り立つ.
別解
- (1)
- 楕円の周 $C$ の点 $\mathrm T(a\cos t,b\sin t)$ ($t$: 実数) における接線 $l$ は
\[\frac{\cos t}{a}x+\frac{\sin t}{b}y = 1 \quad \cdots [1]\]
と表される.
原点 $\mathrm O$ から $l$ に下ろした垂線の足を
とおく.
$\mathrm H(r\cos\theta,r\sin\theta )$ ($r > 0,$ $\theta$: 実数) $l$ は, 点 $\mathrm H$ を通り, ベクトル $(\cos\theta,\sin\theta )$ に垂直であるから, \[\begin{aligned} (x-r\cos\theta )\cos\theta +(y-r\sin\theta )\sin\theta = 0 \\ x\cos\theta +y\sin\theta = r(\cos ^2\theta +\sin ^2\theta ) \\ \frac{\cos\theta}{r}x+\frac{\sin\theta}{r}y = 1 \quad \cdots [2] \end{aligned}\] と表すこともできる. $[1],$ $[2]$ から \[\frac{\cos t}{a} = \frac{\cos\theta}{r}, \quad \frac{\sin t}{b} = \frac{\sin\theta}{r}\] が成り立つので, $\cos ^2t+\sin ^2t = 1$ から \[\begin{aligned} \frac{a^2\cos ^2\theta}{r^2}+\frac{b^2\sin ^2\theta}{r^2} &= 1 \\ a^2\cos ^2\theta +b^2\sin ^2\theta &= r^2 \end{aligned}\] が得られる. よって, \[\mathrm{OH} = \sqrt{a^2\cos ^2\theta +b^2\sin ^2\theta}\] が成り立つ. また, $l$ に垂直な $C$ の接線 $l'$ として, $\mathrm O$ から接線に下ろした垂線の足が \[\mathrm H'\left( r'\cos\left(\theta +\dfrac{\pi}{2}\right),r'\sin\left(\theta +\dfrac{\pi}{2}\right)\right)\] であるようなものがとれて, \[\begin{aligned} \mathrm{OH}' &= \sqrt{a^2\cos ^2\left(\theta +\frac{\pi}{2}\right) +b^2\sin ^2\left(\theta +\frac{\pi}{2}\right)} \\ &= \sqrt{a^2\sin ^2\theta +b^2\cos ^2\theta} \end{aligned}\] が成り立つ. ゆえに, $R$ の隣り合う $2$ 辺が $l,$ $l'$ 上にあるとき, その対角線の長さは \[\begin{aligned} L &= 2\sqrt{\mathrm{OH}^2+{\mathrm{OH}'}^2} \\ &= 2\sqrt{(a^2\cos ^2\theta +b^2\sin ^2\theta )+(a^2\sin ^2\theta +b^2\cos ^2\theta )} \\ &= 2\sqrt{a^2+b^2} \end{aligned}\] であり, $R$ のとり方によらず一定である.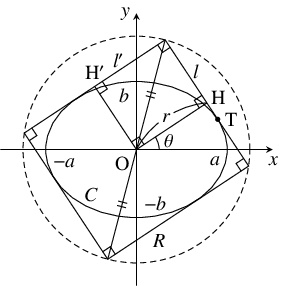
- (2)
- $R$ の隣り合う $2$ 辺が (1) の $l,$ $l'$ $\left( -\dfrac{\pi}{2} \leqq \theta \leqq \dfrac{\pi}{2}\right)$ 上にあるとき, その面積は \[\begin{aligned} S &= 2\mathrm{OH}\cdot 2\mathrm{OH}' \\ &= 4\sqrt{a^2\cos ^2\theta +b^2\sin ^2\theta}\sqrt{a^2\sin ^2\theta +b^2\cos ^2\theta } \\ &= 4\sqrt{(a^4+b^4)\sin ^2\theta\cos ^2\theta +a^2b^2(\cos ^4\theta +\sin ^4\theta )} \\ &= 4\sqrt{(a^4+b^4)\sin ^2\theta\cos ^2\theta +a^2b^2(1-2\sin ^2\theta\cos ^2\theta )} \\ &= 4\sqrt{a^2b^2+(a^4+b^4-2a^2b^2)\sin ^2\theta\cos ^2\theta} \\ &= 4\sqrt{a^2b^2+\frac{(a^2-b^2)^2}{4}\sin ^22\theta} \end{aligned}\] である. $\sin ^22\theta = 1$ つまり $\theta = \pm\dfrac{\pi}{4}$ のとき, $S$ は最大値 \[ 4\sqrt{a^2b^2+\frac{(a^2-b^2)^2}{4}} = 4\sqrt{\frac{(a^2+b^2)^2}{4}} = 2(a^2+b^2)\] をとる.
参考
(1) の結果から, 楕円の周 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$ に向かって互いに直交する $2$ 本の接線が引けるような点の軌跡は円周 $x^2+y^2 = a^2+b^2$ であることがわかる.
この円を楕円の「準円」(director circle, orthoptic circle) と呼ぶ.
問題《アイゼンシュタインの $3$ つ組の公式の幾何学的証明》
座標平面において, 点 $\mathrm A(-1,0)$ を通る傾き $t$ の直線と楕円の周 $x^2+xy+y^2 = 1$ の交点を $\mathrm P(x,y)$ $(x,\ y > 0)$ とおく.
- (1)
- $t$ を用いて $x,$ $y$ を表せ.
- (2)
- $x,$ $y$ が有理数のとき, $t$ は有理数であることを示せ.
- (3)
- $t$ を $0 < t < 1$ なる有理数とする. このとき, $x,$ $y$ は互いに素な正の整数 $m,$ $n$ $(m > n)$ を用いて \[ x = \frac{m^2-n^2}{m^2+mn+n^2}, \quad y = \frac{2mn+n^2}{m^2+mn+n^2} \quad \cdots [\text A]\] と表されることを示せ.
- (4)
- $a,$ $b,$ $c$ は互いに素な正の整数 $m,$ $n$ $(m > n)$ を用いて \[ a = m^2-n^2,\ b = 2mn+n^2,\ c = m^2+mn+n^2 \quad \cdots [\text B]\] または \[ a = \frac{m^2-n^2}{3},\ b = \frac{2mn+n^2}{3},\ c = \frac{m^2+mn+n^2}{3} \quad \cdots [\text B]'\] と表される. ただし, $m,$ $n$ を $3$ で割った余りが異なるとき $[\text B],$ 等しいとき $[\text B]'$ である.
- (5)
- (4) において $m,$ $n$ を $3$ で割った余りが等しいとき, $a,$ $b$ を入れ替え, $m,$ $n$ をそれぞれ $n+\dfrac{m-n}{3},$ $\dfrac{m-n}{3}$ に置き換えると, $a,$ $b,$ $c$ は $[\text B]$ のように表される.
解答例
- (1)
- 点 $\mathrm P(x,y)$ は点 $\mathrm A(-1,0)$ を通る傾き $t$ の直線 \[ y = t(x+1) \quad \cdots [1],\] 楕円の周 \[ x^2+xy+y^2 = 1 \quad \cdots [2]\] の交点であるから, $[1],$ $[2]$ から $y$ を消去した \[\begin{aligned} x^2+tx(x+1)+t^2(x+1)^2 &= 1 \\ (x^2-1)+tx(x+1)+t^2(x+1)^2 &= 0 \\ (x+1)\{ (x-1)+tx+t^2(x+1)\} &= 0 \\ (x+1)\{ (1+t+t^2)x+t^2-1\} &= 0 \end{aligned}\] を満たす. $x \neq -1$ であるから, \[\begin{aligned} x &= \frac{1-t^2}{1+t+t^2} \quad \cdots [3], \\ y &= t\left(\frac{1-t^2}{1+t+t^2}+1\right) = \frac{2t+t^2}{1+t+t^2} \quad \cdots [4] \end{aligned}\] が得られる.
- (2)
- $x,$ $y$ が有理数のとき, \[ t = \frac{y}{x+1}\] は有理数である.
- (3)
- 互いに素な正の整数 $m,$ $n$ を用いて $t = \dfrac{n}{m}$ とおくと, $[3],$ $[4]$ から \[\begin{aligned} x &= \frac{1-\dfrac{n^2}{m^2}}{1+\dfrac{n}{m}+\dfrac{n^2}{m^2}} = \frac{m^2-n^2}{m^2+mn+n^2}, \\ y &= \frac{2\cdot\dfrac{n}{m}+\dfrac{n^2}{m^2}}{1+\dfrac{n}{m}+\dfrac{n^2}{m^2}} = \frac{2mn+n^2}{m^2+mn+n^2} \end{aligned}\] となる. $x > 0,$ $m^2+mn+n^2 > 0$ であるから, $m^2-n^2 > 0$ よって $m > n$ である.
- (4)
- $(x,y) = \left(\dfrac{a}{c},\dfrac{b}{c}\right)$ は $x^2+xy+y^2 = 1$ の正の有理数解であるから, (3) の結果から $x,$ $y$ は互いに素な正の整数 $m,$ $n\ (m > n)$ を用いて $[\text A]$ のように表せる. よって, \[ a:b:c = (m^2-n^2):(2mn+n^2):(m^2+mn+n^2)\] であり, $a,$ $b,$ $c$ は互いに素である (比 $a:b:c$ はこれ以上簡単にならない) から, $m^2-n^2,$ $2mn+n^2,$ $m^2+mn+n^2$ の最大公約数を $g$ とおくと \[ ga = m^2-n^2, \quad gb = 2mn+n^2, \quad gc = m^2+mn+n^2\] となる. よって, $m,$ $n$ を $3$ で割った余りが異なるとき $g = 1$ から $[\text B]$ が得られ, $m,$ $n$ を $3$ で割った余りが等しいとき $g = 3$ から $[\text B]'$ が得られる.
- (5)
- $m,$ $n$ を $3$ で割った余りが等しいとして, $m-n = 3k$ ($k$: 正の整数) とおく.
- このとき, \[\begin{aligned} a &= \frac{(n+3k)^2-n^2}{3} = 2nk+3k^2 = 2(n+k)k+k^2, \\ b &= \frac{2(n+3k)n+n^2}{3} = n^2+2nk = (n+k)^2-k^2, \\ c &= \frac{(n+3k)^2+(n+3k)n+n^2}{3} = n^2+3nk+3k^2 \\ &= (n+k)^2+(n+k)k+k^2 \end{aligned}\] が成り立つ.
- $n+k > k$ である.
- $m = n+3k,$ $n$ は互いに素であるから, $k,$ $n$ は互いに素で, $n+k,$ $n$ も互いに素である.
- $m = n+3k,$ $n$ は互いに素であるから, $(n+k)-k = n$ は $3$ で割り切れず, $n+k,$ $k$ を $3$ で割った余りは異なる.
参考
- 各辺の長さが整数で, $1$ つの内角の大ささが $120^\circ$ である三角形の $3$ 辺の長さは, 余弦定理により $a^2+ab+b^2 = c^2$ を満たす. この方程式の正の整数解を「アイゼンシュタインの $3$ つ組」と呼ぶ. すべての「アイゼンシュタインの $3$ つ組」は, 必要に応じて並べ替えると, 正の整数 $m,$ $n$ ($m,$ $n$ は互いに素, $3$ で割った余りが異なる, $m > n$) を用いて \[ (m^2-n^2,2mn+n^2,m^2+mn+n^2)\] の整数倍の形に表される.
- 各辺の長さが整数で, $1$ つの内角の大ささが $60^\circ$ である三角形の $3$ 辺の長さは, 余弦定理により $a^2-ab+b^2 = c^2$ を満たす. この方程式の正の整数解を「半角アイゼンシュタインの $3$ つ組」と呼ぶ. すべての「半角アイゼンシュタインの $3$ つ組」は, 必要に応じて並べ替えると, 正の整数 $m,$ $n$ ($m,$ $n$ は互いに素, $3$ で割った余りが異なる, $m > 2n$) を用いて \[ (m^2-n^2,2mn-n^2,m^2-mn+n^2)\] または \[\left(\frac{m^2-n^2}{3},\frac{2mn-n^2}{3},\frac{m^2+n^2-mn}{3}\right)\] (場合分けの条件は $m+n$ が $3$ と互いに素か否か) の整数倍の形に表される.
