放物線
放物線
定義《放物線》
平面上で, 定点 $\mathrm F$ と, $\mathrm F$ を通らない定直線 $g$ からの距離が等しい点の軌跡 $C$ を放物線 (parabola) と呼び,
$\mathrm F$ を $C$ の焦点 (focus), $g$ を $C$ の準線 (directrix) と呼ぶ.
また, $C$ の焦点を通り, $g$ に垂直な直線を $C$ の軸 (axis) と呼ぶ.
さらに, $C$ とその軸の交点を $C$ の頂点 (vertex) と呼ぶ.
定理《放物線の標準形》
放物線 $C:y^2 = 4px$ $(p \neq 0)$ の頂点は原点, 焦点は点 $(p,0),$ 準線は直線 $x = -p$ である.
また, $C$ の軸は $x$ 軸である ($C$ は $x$ 軸に関して対称である).
証明
点 $\mathrm F(p,0)$ $(p \neq 0)$ を焦点とし, 直線 $g:x = -p$ を準線とする放物線を $C$ とする.
平面上の点 $\mathrm P(x,y)$ に対して, $\mathrm P$ から $g$ に下ろした垂線の足 ($\mathrm P \in g$ のときは $\mathrm P$ 自身) を $\mathrm H$ とおくと,
\[\begin{aligned}
\mathrm P \in C &\iff \mathrm{PF} = \mathrm{PH} \iff \mathrm{PF}^2 = \mathrm{PH}^2 \\
&\iff (x-p)^2+y^2 = \{ x-(-p)\} ^2 \\
&\iff y^2 = 4px
\end{aligned}\]
となるから, $C$ の方程式は $y^2 = 4px$ である.
また, $(x,y) \in C \iff (x,-y) \in C$ が成り立つから, $C$ の軸は $x$ 軸である.
また, $(x,y) \in C \iff (x,-y) \in C$ が成り立つから, $C$ の軸は $x$ 軸である.
定理《放物線の接線》
放物線 $C:y^2 = 4px$ $(p \neq 0)$ の $C$ 上の点 $\mathrm P_0(x_0,y_0)$ における接線の方程式は
\[ y_0y = 2p(x+x_0)\]
である.
証明
$y^2 = 4px$ の両辺を $x$ で微分すると, $2yy' = 4p$ となり, $y \neq 0$ のとき
\[ y' = \frac{2p}{y}\]
となる.
よって, $\mathrm P_0 \neq (0,0)$ のとき, $C$ の点 $\mathrm P_0$ における接線の傾きは $\dfrac{2p}{y_0}$ であるから, 接線の方程式は
\[\begin{aligned}
y-y_0 &= \frac{2p}{y_0}(x-x_0) \\
yy_0 &= 2p(x-x_0)+y_0{}^2 \\
&= 2p(x-x_0)+4px_0 \\
&= 2p(x+x_0)
\end{aligned}\]
である.
$\mathrm P_0 = (0,0)$ のときの $C$ の接線の方程式 $x = 0$ もこの式で表される.
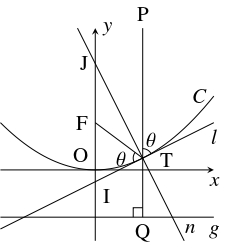
問題《放物線の軸に平行な光の反射》
$a,$ $k$ を正の定数とする.
放物線 $C:y = ax^2$ の焦点を $\mathrm F$ とおく.
また, 点 $\mathrm P(t,k)$ を $C$ の上方にある点として,
点 $\mathrm T(t,at^2)$ における $C$ の接線を $l,$ 法線を $n$ とおき, これらの $y$ 切片をそれぞれ $\mathrm I,$ $\mathrm J$ とおく.
- (A)
- (1)
- $l$ の方程式を求めよ.
- (2)
- $\mathrm{FT} = \mathrm{FI}$ であることを示せ.
- (3)
- $\angle\mathrm{PTJ} = \angle\mathrm{FTJ}$ が成り立つことを示せ.
- (B)
- 折れ線 $\mathrm{PTF}$ の長さ $\mathrm{PT}+\mathrm{TF}$ は点 $\mathrm P$ の取り方によらず一定であることを示せ.
解答例
- (A)
- (1)
- $y = ax^2$ を $x$ で微分すると, $y' = 2ax$ となる.
よって, 点 $\mathrm T(t,at^2)$ における $C$ の接線 $l$ の方程式は
\[ y-at^2 = 2at(x-t)\]
つまり
\[ y = 2atx-at^2 \quad \cdots [1]\]
である.
- (2)
- $C$ の焦点 $\mathrm F$ の座標は $\left( 0,\dfrac{1}{4a}\right)$ であり, $[1]$ から点 $\mathrm I$ の座標は $(0,-at^2)$ であるので, \[\begin{aligned} \mathrm{FT} &= \sqrt{t^2+\left( at^2-\frac{1}{4a}\right) ^2} = \sqrt{a^2t^4+\frac{t^2}{2}+\frac{1}{16a^2}} \\ &= \sqrt{\left(\frac{1}{4a}+at^2\right) ^2} = \frac{1}{4a}+at^2 \\ &= \mathrm{FO}+\mathrm{OI} = \mathrm{FI} \quad \cdots [2] \end{aligned}\] が成り立つ.
- (3)
- $\mathrm{PT},$ $l$ のなす角を $\theta$ とおくと, $[2]$ から $\triangle\mathrm{FTI}$ は二等辺三角形であるので, \[\angle\mathrm{FTI} = \angle\mathrm{FIT} = \theta\] よって \[\angle\mathrm{PTJ} = \angle\mathrm{FTJ} = 90^\circ -\theta\] が成り立つ.
- (B)
- 点 $\mathrm P$ から $C$ の準線 $g:y = -\dfrac{1}{4a}$ に下ろした垂線の足を $\mathrm Q$ とおくと, 放物線の定義により \[\mathrm{PT}+\mathrm{TF} = \mathrm{PT}+\mathrm{TQ} = \mathrm{PQ} = k+\dfrac{1}{4a}\] となる. この値は点 $\mathrm P$ の $x$ 座標によらず一定である.
参考
「パラボラ・アンテナ」は, 放物線を軸のまわりに回転した「回転放物面」と呼ばれる形をしており,
本問で示した放物線の性質を利用して電波を受信している.
問題《放物線の焦点・接線・法線の位置関係》
放物線 $C:y^2 = 4px$ $(p \neq 0)$ 上の任意の点における $C$ の接線, 法線と $C$ の対称軸の交点を結ぶ線分の中点は $C$ の焦点と一致することを示せ.
解答例
$f(y) = \dfrac{y^2}{4p}$ を $y$ で微分すると,
\[ f'(y) = \dfrac{y}{2p}\]
となる.
よって, 放物線 $C:x = \dfrac{y^2}{4p}$ 上の点 $\mathrm P(s,t)$ における $C$ の接線, 法線の方程式は, それぞれ
\[\begin{aligned}
x-s &= \frac{t}{2p}(y-t) \quad \cdots [1], \\
x-s &= -\frac{2p}{t}(y-t) \quad \cdots [2]
\end{aligned}\]
である.
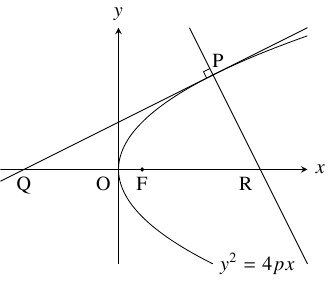また, 点 $\mathrm P$ は $C$ 上にあるから,
\[ t^2 = 4ps \quad \cdots [3]\]
が成り立つ.
$[1],$ $[2]$ に $y = 0$ を代入すると
\[\begin{aligned}
x &= -\frac{t^2}{2p}+s = -\frac{4ps}{2p}+s = -s \quad (\because [3]), \\
x &= \frac{2pt}{t}+s = 2p+s
\end{aligned}\]
となるから, 直線 $[1],$ $[2]$ と $C$ の対称軸である $x$ 軸は, それぞれ点 $\mathrm Q(-s,\ 0),$ $\mathrm R(2p+s,\ 0)$ で交わる.
これら点の $C$ の焦点 $\mathrm F(p,\ 0)$ からの距離は,
\[\begin{aligned}
\mathrm{FQ} &= |(-s)-p| = |p+s|, \\
\mathrm{FR} &= |(2p+s)-p| = |p+s|
\end{aligned}\]
である.
ゆえに, $\mathrm{FQ} = \mathrm{FR}$ から, 線分 $\mathrm{QR}$ の中点は $C$ の焦点 $\mathrm F$ と一致する.
問題《放物線上の調和点列》
$xy$ 平面において, 放物線 $C:y = x^2$ とその下側にある点 $\mathrm P(p,p')$ $(p' < p^2)$ を考える.
点 $\mathrm P$ を通るような $C$ の $2$ 本の接線を考え, その接点をそれぞれ $\mathrm A(a,a^2),$ $\mathrm B(b,b^2)$ とおく.
また, 点 $\mathrm P$ を通る傾き $m$ の直線が $C$ と相異なる $2$ 点 $\mathrm S(s,s^2),$ $\mathrm T(t,t^2)$ で交わるとする.
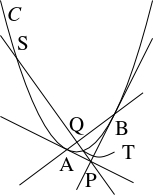
- (1)
- $p,$ $p'$ を用いて $a+b,$ $ab$ を表せ.
- (2)
- $p,$ $p',$ $m$ を用いて $s+t,$ $st$ を表せ.
- (3)
- 直線 $\mathrm{AB}$ と直線 $\mathrm{ST}$ の交点を $\mathrm Q$ とし, $\mathrm Q$ の $x$ 座標を $q$ とおく. $s < q < t < p$ となる場合について, 等式 \[\frac{1}{\mathrm{PS}}+\frac{1}{\mathrm{PT}} = \frac{2}{\mathrm{PQ}}\] が成り立つことを示せ.
(参考: $2006$ 神戸大)
解答例
- (1)
- 点 $\mathrm A(a,a^2)$ における $C$ の接線の方程式は,
$y-a^2 = 2a(x-a)$ つまり $y = 2ax-a^2$である. 同様に, 点 $\mathrm B(b,b^2)$ における $C$ の接線の方程式は \[ y = 2bx-b^2\] である. よって, 点 $\mathrm P(p,p')$ はこれらの接線の交点であるから, \[ a^2-2ap+p' = b^2-2bp+p' = 0\] が成り立つ. よって, $a,$ $b$ は $u$ の $2$ 次方程式 \[ u^2-2pu+p' = 0\] の $2$ 解であるから, 解と係数の関係により \[ a+b = 2p, \quad ab = p'\] である.
- (2)
- 直線 $\mathrm{PQ}:y = m(x-p)+p'$ と $C$ の交点の $x$ 座標は \[ x^2-mx+mp-p' = 0\] を満たす. この $x$ の $2$ 次方程式の解が $s,$ $t$ であるから, 解と係数の関係により \[ s+t = m, \quad st = mp-p'\] である.
- (3)
- $\mathrm P,$ $\mathrm Q,$ $\mathrm S,$ $\mathrm T$ から $x$ 軸に下ろした垂線の足を $\mathrm P_1,$ $\mathrm Q_1,$ $\mathrm S_1,$ $\mathrm T_1$ とおく. $\dfrac{1}{\mathrm P_1\mathrm S_1}+\dfrac{1}{\mathrm P_1\mathrm T_1} = \dfrac{2}{\mathrm P_1\mathrm Q_1}$ が成り立つことを示せばよい. \[\begin{aligned} &\frac{1}{\mathrm P_1\mathrm S_1}+\frac{1}{\mathrm P_1\mathrm T_1} = \frac{1}{p-s}+\frac{1}{p-t} \\ &= \frac{2p-(s+t)}{(p-s)(p-t)} = \frac{2p-m}{p^2-p'}, \\ &\frac{2}{\mathrm P_1\mathrm Q_1} = \frac{2}{p-q} \\ &= \frac{2}{p-\dfrac{mp-2p'}{m-2p}} = \frac{2(m-2p)}{-2p^2+2p'} \\ &= \frac{2p-m}{p^2-p'} \end{aligned}\] であるから, $\dfrac{1}{\mathrm P_1\mathrm S_1}+\dfrac{1}{\mathrm P_1\mathrm T_1} = \dfrac{2}{\mathrm P_1\mathrm Q_1}$ が成り立つ.
参考
異なる $4$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ がこの順に同一直線上に並ぶとき, 次の条件は同値である.
これらの条件の $1$ つ (よって全部) が成り立つとき, $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ は「調和点列」(harmonic range of points) をなすという.
- (i)
- $\mathrm{AB}\cdot\mathrm{BC} = \mathrm{AD}\cdot\mathrm{DC}$ が成り立つ.
- (ii)
- $\dfrac{1}{\mathrm{AB}},$ $\dfrac{1}{\mathrm{AC}},$ $\dfrac{1}{\mathrm{AD}}$ は等差数列をなす.
- (iii)
- 線分 $\mathrm{BD}$ の中点 $\mathrm M$ について, $\mathrm{AB}\cdot\mathrm{AD} = \mathrm{AC}\cdot\mathrm{AM}$ が成り立つ.