不等式の表す領域
曲線の通過領域
問題《直線の通過領域》
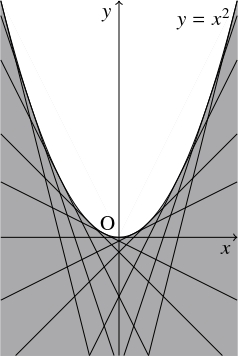
$t$ が実数全体を動くとき, 直線 $y = 2tx-t^2$ が通過する領域を求めよ.
(参考: $2019$ 三重大)
解答例
ある実数 $t$ に対して点 $(x,y)$ が直線 $y = 2tx-t^2$ 上にあるとき, $t$ の $2$ 次方程式
\[ t^2-2xt+y = 0\]
は実数解をもつから, その判別式 $D$ について
$\dfrac{D}{4} = x^2-y \geqq 0$ つまり $y \leqq x^2$
が成り立つ.
ゆえに, 求める領域は, 放物線 $y = x^2$ の下方の部分である.
ただし, 境界線上の点を含む.

別解
直線の方程式 $y = 2tx-t^2$ は
\[ y = -(t-x)^2+x^2\]
と変形でき, $-(t-x)^2$ は $0$ 以下の任意の実数の値をとるから, $y \leqq x^2$ が成り立つ.
よって, 求める領域は放物線 $y = x^2$ の下方の部分である.
ただし, 境界線上の点を含む.
参考
直線 $y = 2tx-t^2$ は点 $(t,t^2)$ における放物線 $y = x^2$ の接線であり,
放物線 $y = x^2$ は方程式が $y = 2tx-t^2$ ($t$: 実数) の方程式で表される直線すべてに接する曲線として定まる.
一般に, $t$ がさまざまな値をとるとき, $x,$ $y$ の方程式 $f(x,y,t) = 0$ で表される曲線すべてに接する定曲線を, それらの曲線の「包絡線」(envelope) と呼ぶ.
領域と最大・最小
問題《じゃんけんに関する線形計画問題》
A, B の $2$ 人が $1$ 回じゃんけんを行う.
グー, チョキ, パーを出す確率はそれぞれ, A が $p,$ $q,$ $1-p-q,$ B が $x,$ $y,$ $1-x-y$ であり, $2$ 人の手の出し方は独立であるとする.
B が勝つ確率を $w,$ 負ける確率を $l$ とおく.
- (1)
- $x,$ $y,$ $p,$ $q$ を用いて $w-l$ を表せ.
- (2)
- $p,$ $q$ が次の条件を満たすとき, $w-l$ を最大にする $x,$ $y$ の値を求めよ.
- (i)
- $p < \dfrac{1}{3} < q$ かつ $p+q > \dfrac{2}{3}$ のとき.
- (ii)
- $p > \dfrac{1}{3}$ かつ $q > \dfrac{1}{3}$ のとき.
(参考: 福井医大)
解答例
- (1)
- B が勝つのは, A, B が (グー, パー), (チョキ, グー), (パー, チョキ) を出す場合で, その確率 $w$ は \[ w = p(1-x-y)+qx+(1-p-q)y\] である. 同様に, B が負ける確率 $l$ は, \[ l = py+q(1-x-y)+(1-p-q)x\] である. ゆえに, $w-l$ は \[ w-l = 3qx-3py-x+y+p-q\] と表される.
- (2)
- $w-l = (3q-1)x+(1-3p)y+p-q$ であるから, 条件
\[ 0 \leqq x \leqq 1 \quad \cdots [1], \quad 0 \leqq y \leqq 1 \quad \cdots[2]\]
と, $0 \leqq 1-x-y \leqq 1$ つまり
\[ 0 \leqq x+y \leqq 1 \quad \cdots [3]\]
のもとで, $k = (3q-1)x+(1-3p)y$ を最大にする $x,$ $y$ の値を求めればよい.
- (i)
- $p < \dfrac{1}{3} < q$ かつ $p+q > \dfrac{2}{3}$ のとき.
$\dfrac{1-3q}{1-3p} < -1$ であるから, $xy$ 平面上の直線
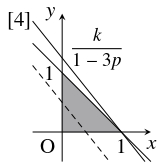
\[ y = \frac{1-3q}{1-3p}x+\frac{k}{1-3p} \quad \cdots [4]\]
が $[1]$~$[3]$ の表す領域と共有点をもつとき,
$y$ 切片 $\dfrac{k}{1-3p}$ は $[4]$ が点 $(1,0)$ を通るとき最大になる.
$1-3p > 0$ であるから, このとき $k$ は最大になる.
- (ii)
- $p > \dfrac{1}{3}$ かつ $q > \dfrac{1}{3}$ のとき. $\dfrac{1-3q}{1-3p} > 0$ であるから, $xy$ 平面上の直線 $[4]$ が $[1]$~$[3]$ の表す領域と共有点をもつとき, $y$ 切片 $\dfrac{k}{1-3p}$ は $[4]$ が点 $(1,0)$ を通るとき最小になる. $1-3p < 0$ であるから, このとき $k$ は最大になる.
参考
- (i) は A がチョキを出す確率が他の手よりも高い場合, (ii) は A がパーを出す確率が他の手よりも低い場合を表す. これらの場合には, B が必ずグーを出すようにすれば, B の勝つ確率と負ける確率の差が最大になることがわかった.
- 上記のように, $1$ 次不等式で表されるいくつかの条件のもとで $1$ 次式の最大値・最小値を求める問題を「線形計画問題」(linear programming problem) と呼ぶ.
