軌跡
軌跡
問題《アポロニウスの円》
$m,$ $n$ を相異なる正の数とする.
$xy$ 平面上において, $2$ 点 $\mathrm A(-1,0),$ $\mathrm B(1,0)$ からの距離の比が $m:n$ である点 $\mathrm P$ の軌跡を求めよ.
標準素朴$2015/06/27$$2022/05/24$
解答例
点 $\mathrm P(x,y)$ に対して
\[\begin{aligned}
&\mathrm{AP}:\mathrm{BP} = m:n \\
&\iff m\mathrm{BP} = n\mathrm{AP} \\
&\iff m^2\mathrm{BP}^2 = n^2\mathrm{AP}^2 \\
&\iff m^2\{ (x-1)^2+y^2\} = n^2\{ (x+1)^2+y^2\} \\
&\iff (m^2-n^2)x^2-2(m^2+n^2)x+(m^2-n^2)y^2 = n^2-m^2 \\
&\iff x^2-2\cdot\frac{m^2+n^2}{m^2-n^2}x+y^2 = -1 \\
&\iff \left( x-\frac{m^2+n^2}{m^2-n^2}\right) ^2+y^2 = \frac{(m^2+n^2)^2}{(m^2-n^2)^2}-1 \\
&\iff \left( x-\frac{m^2+n^2}{m^2-n^2}\right) ^2+y^2 = \frac{(m^2+n^2)^2-(m^2-n^2)^2}{(m^2-n^2)^2} \\
&\iff \left( x-\frac{m^2+n^2}{m^2-n^2}\right) ^2+y^2 = \frac{4m^2n^2}{(m^2-n^2)^2} \\
\end{aligned}\]
が成り立つから, 点 $\mathrm P$ の軌跡は $\left(\dfrac{m^2+n^2}{m^2-n^2},0\right)$ を中心とする半径 $\dfrac{2mn}{|m^2-n^2|}$ の円周である.
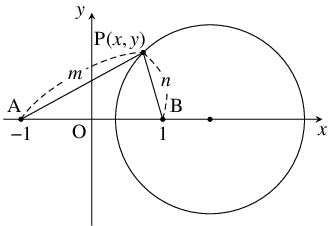
参考
- 本問で示したように, 相異なる $2$ 定点からの距離の比が一定である点の軌跡は円周である(ただし, $1:1$ の場合は除く). この円を「アポロニウスの円」(circle of Apollonius)と呼ぶ.
- 相異なる $2$ 定点 $\mathrm A,$ $\mathrm B$ からの距離の比が $1:1$ である点の軌跡は線分 $\mathrm{AB}$ の垂直二等分線である.
問題《座標軸を結ぶ線分の中点の軌跡》
$x$ 軸上の点 $\mathrm P$ と $y$ 軸上の点 $\mathrm Q$ が $\mathrm{PQ} = 2$ を満たしながら動くとき,
線分 $\mathrm{PQ}$ の中点 $\mathrm R$ の軌跡を求めよ.
基本素朴$2021/10/22$$2021/10/22$
解答例
$\mathrm P(p,0),$ $\mathrm Q(0,q),$ $\mathrm R(x,y)$ とおく.
このとき, 条件 $\mathrm{PQ} = 2$ から, \[ p^2+q^2 = 4 \quad \cdots [1]\] が成り立つ. また, 点 $\mathrm R$ は線分 $\mathrm{PQ}$ の中点であるから, \[ x = \frac{1}{2}p, \quad y = \frac{1}{2}q\] が成り立つ. よって, \[ p = 2x, \quad q = 2y \quad \cdots [2]\] であるから, $[1]$ に $[2]$ を代入すると \[ 4x^2+4y^2 = 4\] つまり \[ x^2+y^2 = 1\] が得られる. ゆえに, 点 $\mathrm R$ の軌跡は, 単位円の周である.
このとき, 条件 $\mathrm{PQ} = 2$ から, \[ p^2+q^2 = 4 \quad \cdots [1]\] が成り立つ. また, 点 $\mathrm R$ は線分 $\mathrm{PQ}$ の中点であるから, \[ x = \frac{1}{2}p, \quad y = \frac{1}{2}q\] が成り立つ. よって, \[ p = 2x, \quad q = 2y \quad \cdots [2]\] であるから, $[1]$ に $[2]$ を代入すると \[ 4x^2+4y^2 = 4\] つまり \[ x^2+y^2 = 1\] が得られる. ゆえに, 点 $\mathrm R$ の軌跡は, 単位円の周である.
問題《円の準円》
円周 $C:x^2+y^2 = r^2$ に向かって互いに直交する $2$ 本の接線が引けるような点 $\mathrm P$ の軌跡を求めよ.
標準定理$2022/11/30$$2022/12/02$
解答例
点 $(p,q)$ を通る傾き $m$ の直線 $m(x-p)-(y-q) = 0$ が円周 $C:x^2+y^2 = r^2$ に接するとする.
このとき,
\[\frac{|m(-p)-(-q)|}{\sqrt{m^2+(-1)^2}} = r\]
が成り立つ.
両辺を $2$ 乗して得られる $2$ 次方程式
\[\begin{aligned}
(mp-q)^2 &= r^2(m^2+1) \\
(p^2-r^2)m^2-2pqm+(q^2-r^2) &= 0 \quad \cdots [1]
\end{aligned}\]
は, 判別式が
\[ 4p^2q^2-4(p^2-r^2)(q^2-r^2) = 4r^2(p^2+q^2-r^2) > 0\]
であるから, 相異なる $2$ つの実数解をもつ.
点 $\mathrm P(p,q)$ を通って傾きが $m_1,$ $m_2$ である $C$ の接線が直交するとき, $[1]$ は相異なる $2$ つの実数解 $m = m_1,$ $m_2$ をもつから, 解と係数の関係により
\[\begin{aligned}
&-1 = m_1m_2 = \frac{q^2-r^2}{p^2-r^2} \\
&p^2+q^2 = 2r^2
\end{aligned}\]
が成り立つ.
ゆえに, 点 $\mathrm P$ は原点を中心とする半径 $\sqrt 2r$ の円周を描く.